Towards Understanding Evolving Patterns in Sequential Data

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides a novel, quantitative measure (EVORATE) for evaluating evolving patterns in sequential data which has been a largely qualitative task previously. This impacts various machine learning fields by enabling better model selection, feature engineering, and temporal analysis, opening avenues for improved forecasting, classification, and other sequential tasks.

Visual Insights

#

This figure compares the performance of the proposed EVORATE and EVORATEw methods for estimating mutual information in sequential data. Panels (a) and (b) show the results for data with clear correspondence between time steps, comparing EVORATE with two different critic network architectures (concatenated and separable). Panels (c) and (d) illustrate the performance of EVORATEw, designed for data without direct correspondence, using either an identity function or a neural network for the encoding (g). The plots show the estimated mutual information (MI) over training steps, compared against the true MI value.

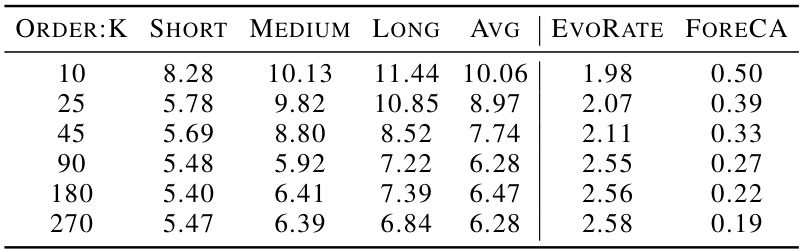
This table presents the results of time series forecasting experiments on the M4-Weekly dataset. It shows the impact of varying the order (k) of the autoregressive model on the forecasting performance, measured by the Symmetric Mean Absolute Percentage Error (sMAPE). The sMAPE is calculated separately for short, medium, and long forecasting horizons, as well as an overall average. The table also includes the EVORATE and ForeCA values for each model order. EVORATE quantifies the evolving patterns in the data, while ForeCA measures the forecastibility of the time series.

In-depth insights

#

Evolving Patterns

#

The concept of “evolving patterns” in sequential data is a significant focus, highlighting the limitations of traditional autoregressive models which assume static patterns. The core contribution is quantifying these evolving patterns using a novel measure, EVORATE, based on mutual information between past and future data points. This addresses the critical need for a standardized, quantitative measure, moving beyond subjective assessments. EVORATE’s efficacy is demonstrated across various datasets, showcasing its ability to determine the suitability of sequential models and inform feature selection. A key challenge addressed is the lack of correspondence between data points across disparate timestamps, which is cleverly overcome by incorporating optimal transport to estimate EVORATEW. The theoretical justification of EVORATE and its connection to autoregressive model performance further strengthens its value. Overall, the work offers a significant advance in understanding and utilizing evolving patterns in various sequential learning tasks.

EVORATE Metric

#

The EVORATE metric, proposed for quantifying evolving patterns in sequential data, is a novel approach leveraging mutual information. Its key innovation lies in explicitly considering the temporal dependency between data points, unlike traditional mutual information estimation methods. This is achieved by estimating the mutual information between the next data point and a compressed representation of the preceding sequence, effectively capturing the evolving pattern’s strength. EVORATE addresses limitations of existing methods by providing a principled way to determine the presence of evolving patterns, gauge their temporal influence, and assess feature relevance. While computationally efficient, it faces challenges when data points lack clear correspondence across timestamps. The proposed EVORATEw extension addresses this, ingeniously using optimal transport to establish such correspondences. Experiments demonstrate EVORATE’s effectiveness in various applications, validating its ability to quantify evolving patterns in diverse data modalities. However, future work might investigate its robustness against noise, its scalability to ultra-high-dimensional datasets, and its applicability to specific tasks beyond forecasting and classification.

Optimal Transport

#

Optimal transport (OT) is a powerful mathematical framework that elegantly addresses the problem of efficiently moving mass from one distribution to another. Its application in machine learning is rapidly expanding because it provides a principled way to compare probability distributions, going beyond simple metrics like Euclidean distance that often fail to capture complex relationships. In the context of the provided text, OT is crucial for the EVORATEw method. Because time series data may lack a direct correspondence between data points across different timestamps, OT is used to establish a mapping that creates this correspondence, enabling accurate calculation of mutual information, a key component of the evolving pattern analysis. This is particularly important for high-dimensional data, where establishing correspondence without OT becomes computationally prohibitive. By leveraging OT’s ability to find optimal mappings in Wasserstein distance space, EVORATEw overcomes the limitation of traditional mutual information estimators which struggle in these scenarios, leading to more robust and accurate measurement of evolving patterns in sequential data. This exemplifies the value of OT in bridging gaps in data analysis, thus enabling more sophisticated and insightful sequential data modeling.

Empirical Studies

#

An Empirical Studies section would rigorously evaluate the proposed method’s performance. It would likely involve experiments on multiple diverse datasets, comparing results to existing state-of-the-art techniques. Careful attention to experimental design would be crucial, including proper data splitting (training, validation, testing), hyperparameter tuning strategies, and the use of appropriate evaluation metrics. The results would be presented clearly, likely with tables and figures illustrating performance gains or improvements in specific aspects of the problem. Statistical significance testing would be essential to support claims of improved performance, ruling out the possibility of results being due to random chance. Detailed analysis of the results across different datasets and experimental conditions would reveal the method’s strengths and weaknesses, providing valuable insights into its applicability and limitations. Furthermore, an ablation study, systematically removing components of the proposed method, could help isolate the contributions of specific elements. Finally, the section should discuss any limitations encountered during the empirical evaluation and provide suggestions for future research directions.

Future Works

#

Future work could explore extending EVORATE’s capabilities to higher-order temporal dependencies and more complex data structures. Investigating its performance on diverse data modalities such as audio and text would be valuable, along with rigorous comparison against established methods. Furthermore, research into more efficient computational implementations is crucial for broader applicability. A key area of focus should be developing more robust methods for handling cases with missing data or inconsistent sampling rates in real-world scenarios. Finally, exploring applications of EVORATE in various downstream tasks, such as anomaly detection and causal inference, could provide significant insights into its practical value. In addition, a deeper investigation into the theoretical properties of EVORATE and its relationship to other information-theoretic measures may reveal more fundamental insights. Addressing the computational complexity of EVORATEW, especially for high-dimensional datasets, is vital for practical application.

More visual insights

#

More on figures

This figure shows the performance of EVORATE and EVORATEw on mutual information estimation tasks. Panels (a) and (b) compare the performance of EVORATE using different critic network architectures (concatenated vs. separable) on sequential data with correspondence between data points. Panels (c) and (d) demonstrate the performance of EVORATEw, which addresses situations without correspondence, using different encoder functions (identity vs. neural network). The plots illustrate how the estimated mutual information converges to the true mutual information over training steps under various conditions.

This figure shows the performance comparison of EVORATE and EVORATEw in mutual information estimation. (a) and (b) demonstrate EVORATE’s performance on sequential data with correspondence, comparing different critic function architectures. (c) and (d) illustrate EVORATEw’s performance on data without correspondence, showcasing the impact of different encoding functions (g) on the estimation accuracy.

More on tables

This table presents a comparison of the estimated mutual information (using EVORATE and ForeCA methods) and the state-of-the-art (SOTA) performance for time series forecasting tasks across various datasets (Crypto, Player Trajectory, M4-Monthly, M4-Weekly, and M4-Daily). The RMSE (root mean squared error) and sMAPE (symmetric mean absolute percentage error) metrics are used to evaluate the SOTA forecasting model’s performance. The table shows that EVORATE generally provides higher mutual information estimates than ForeCA, implying a better ability to capture evolving patterns in sequential data. The SOTA performance varies across different datasets, suggesting that the effectiveness of the model depends on the dataset’s characteristics.

This table presents the estimated mutual information (EVORATEW) and the classification accuracy for both invariant and evolving learning methods across seven different datasets. The ‘ACC_Evo - ACC_Inv’ column shows the improvement in accuracy achieved by using the evolving learning method compared to the invariant learning method. The EVORATEW values provide a quantitative measure of the evolving patterns in each dataset, indicating the suitability of applying evolving learning methods.

This table compares the classification accuracy of the proposed method against several baseline methods across various synthetic and real-world datasets. The accuracy is averaged across multiple target domains for each dataset, providing a comprehensive comparison of performance.

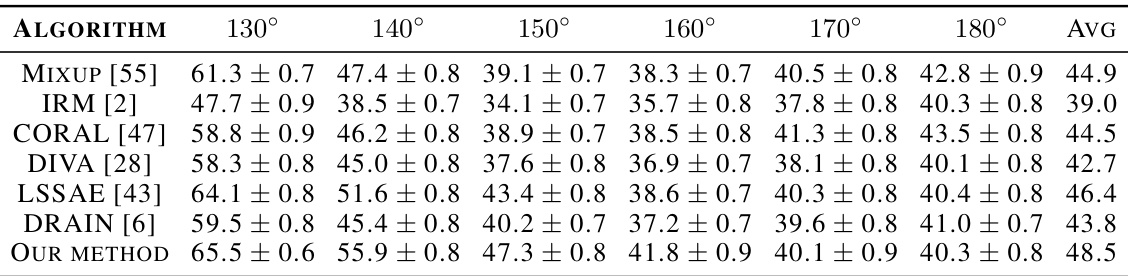
This table compares the classification accuracy of the proposed method against several baseline methods across various synthetic and real-world datasets. The accuracy is averaged across multiple target domains for a comprehensive evaluation. The results highlight the superior performance of the proposed method compared to the existing state-of-the-art techniques.

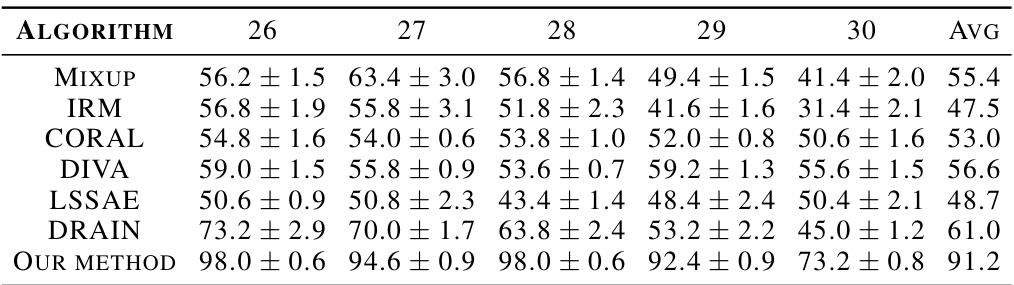
This table presents the classification accuracy results for the Rotated Gaussian dataset in the Evolving Domain Generalization (EDG) task. The results are broken down by target domain (26-30) and compare different algorithms (MIXUP, IRM, CORAL, DIVA, LSSAE, DRAIN) to the proposed method. Each algorithm’s performance is presented as an average accuracy across multiple runs, with standard deviation indicated. This allows for a direct comparison of the performance of various domain generalization techniques on this specific dataset in terms of generalization ability.

This table presents the results of the Rotated Gaussian experiment in the Evolving Domain Generalization (EDG) tasks. Each column represents a different target domain (numbered 21-30), and each row shows the performance of different algorithms (MIXUP, IRM, CORAL, DIVA, LSSAE, DRAIN, and the proposed method). The values are the average accuracy of each algorithm’s performance on that target domain, including standard deviation. The table aims to show how well different algorithms generalize to evolving domains in this specific dataset.

This table compares the estimated mutual information (using EVORATE) with the performance of a state-of-the-art (SOTA) time series forecasting method on various datasets (Crypto, Player Traj., M4-Monthly, M4-Weekly, M4-Daily). The RMSE/SMAPE values represent the error rate of the SOTA method. The table highlights the relationship between EVORATE scores and forecasting performance across different dataset types.

Full paper

#