↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Convolutional Graph Neural Networks (GNNs), while successful, suffer from limitations like over-smoothing, over-squashing, and limited expressiveness. These issues stem from their reliance on convolutional operations that restrict their ability to capture complex graph structures and long-range dependencies. Addressing these limitations is crucial for advancing GNN research and expanding their applicability to real-world problems.
This paper introduces RUM (Random Walk with Unifying Memory), a novel GNN architecture that eliminates convolutional operations. RUM leverages Recurrent Neural Networks (RNNs) to process topological and semantic features extracted from random walks on the graph. The theoretical analysis and experimental results demonstrate that RUM surpasses the expressiveness of the Weisfeiler-Lehman isomorphism test, alleviates over-smoothing and over-squashing, and achieves competitive performance on various graph learning tasks, showing potential for more powerful and efficient graph analysis.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in graph neural networks (GNNs) due to its significant advancement in addressing the limitations of convolution-based GNNs. It introduces a novel, non-convolutional approach that surpasses the expressiveness of existing methods, enhancing the efficiency and robustness of GNNs while achieving competitive performance. This opens new avenues for research focusing on improving GNN expressiveness, scalability, and the design of more efficient graph learning models.
Visual Insights#

This figure demonstrates the difference in expressiveness between RUM and the Weisfeiler-Lehman (WL) test. It shows two graphs that are indistinguishable by the WL test and WL-equivalent Graph Neural Networks (GNNs), but which RUM can easily distinguish. This highlights RUM’s ability to capture more subtle structural information within graphs, exceeding the limitations of convolutional GNNs.

This table provides a schematic illustration of the RUM (Random Walk with Unifying Memory) neural network. It showcases all possible 4-step unbiased random walks originating from a 2-degree carbon atom within the propylene oxide molecule. Each walk is visually represented, showing the path taken and the order of node visits. The table also shows the semantic (features of nodes visited) and topological (order of unique nodes visited) representations associated with each walk, highlighting how RUM combines these aspects for node embeddings.
In-depth insights#
RUM: A Novel GNN#
The proposed model, RUM (Random Walk with Unifying Memory), presents a novel approach to graph neural networks (GNNs). Instead of relying on convolutional operations, RUM leverages the power of recurrent neural networks (RNNs) to process information gathered from random walks on the graph. This innovative design directly addresses the limitations of convolution-based GNNs, such as over-smoothing and limited expressiveness. By merging topological and semantic features along random walks, RUM effectively captures long-range dependencies and offers a more expressive representation learning capability. Theoretical analysis shows that RUM surpasses the expressive power of the Weisfeiler-Lehman test, a significant achievement in GNN research. Furthermore, experimental results demonstrate that RUM achieves competitive performance while exhibiting robustness and efficiency compared to conventional GNNs across various tasks. The absence of convolution operators makes RUM inherently more scalable and memory-efficient when processing large graphs. This work is significant for its novel architecture and the improvements over existing approaches.
Expressive Power#
The concept of “Expressive Power” in the context of graph neural networks (GNNs) centers on a model’s ability to capture and distinguish the structural properties of graphs. A GNN with high expressive power can discern subtle differences between graphs that might be indistinguishable to simpler models. The Weisfeiler-Lehman (WL) test serves as a benchmark for expressive power, as it represents a theoretical upper bound on the capabilities of many GNN architectures. The paper likely investigates whether the proposed non-convolutional GNN surpasses the limitations of the WL test, potentially demonstrating the ability to learn graph properties beyond what is achievable using convolution-based methods. This enhanced expressive power is crucial for complex tasks where subtle graph structural differences are key for accurate classification, such as in molecule modeling or social network analysis. The analysis likely involves comparing the performance of different GNNs on graph isomorphism problems and carefully designed tasks where subtle differences in graphs are critical, demonstrating a clear advantage in discerning such features. Theoretical analysis, including a mathematical proof, might be presented to underpin the claim of increased expressiveness. Ultimately, a strong emphasis on enhanced expressive power indicates a significant advancement in GNN capabilities, broadening the potential applications for GNNs in various domains.
Over-smoothing Fix#
Over-smoothing, a significant challenge in graph neural networks (GNNs), arises from repeated application of graph convolution, leading to homogenization of node representations and hindering the network’s ability to distinguish nodes effectively. Addressing this issue is crucial for improving GNN performance, particularly in tasks requiring the preservation of fine-grained node distinctions or long-range dependencies. Various methods have been proposed to mitigate over-smoothing, including the use of residual connections, attention mechanisms, and graph rewiring techniques. Each of these approaches offers advantages and disadvantages. Residual connections help maintain gradient flow during deeper network training, but their effectiveness can be limited when dealing with severe over-smoothing. Attention mechanisms, while capable of focusing on relevant neighbors, may introduce computational overhead and require careful tuning. Graph rewiring, on the other hand, aims to enhance the structural information in the graph by modifying the adjacency matrix, but this can be a challenging task that may inadvertently introduce artifacts or inaccuracies. The optimal solution to the over-smoothing problem often depends on the specific application and graph structure, requiring careful consideration of the trade-offs between complexity, computational cost, and performance gains.
RUM Performance#
The RUM (Random Walk with Unifying Memory) model demonstrates strong performance across diverse graph-level and node-level tasks. Its expressiveness surpasses that of convolutional GNNs, effectively addressing limitations such as over-smoothing and over-squashing. Empirical results consistently show RUM achieving competitive accuracy with state-of-the-art models, particularly excelling on tasks requiring long-range dependencies. Notably, RUM exhibits efficiency advantages, outperforming convolutional counterparts in speed, especially when leveraging GPU acceleration. While dense graphs pose a slight challenge, its performance on large-scale datasets highlights its scalability. The robustness of RUM against adversarial attacks further underscores its practical viability. Overall, the experimental evidence strongly supports RUM as a significant advancement in graph neural network architecture.
Future Directions#
The “Future Directions” section of this research paper suggests several promising avenues for future work. Theoretically, the authors plan to expand their analytical framework to incorporate factors like layer width and depth, aiming for a more precise understanding of how these parameters influence the model’s ability to capture key graph properties. Experimentally, they propose extending their model to address larger and more complex graphs, as well as exploring the incorporation of uncertainty into the model’s design. The authors also highlight the potential of applying their non-convolutional approach to other fields, particularly physics-based graph modeling, suggesting applications in drug discovery and the modeling of n-body systems. This demonstrates a forward-looking approach that acknowledges both theoretical limitations and practical applications, paving the way for more robust and widespread applications of the proposed methodology.
More visual insights#
More on figures
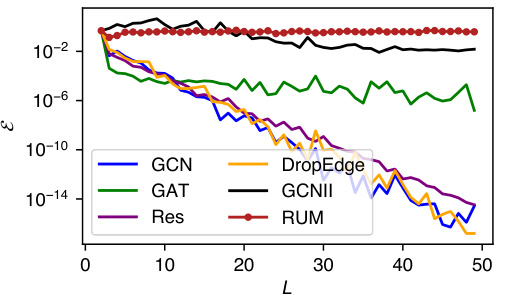
This figure shows how the Dirichlet energy, a measure of the dissimilarity between node representations in a graph, changes over multiple layers (or steps) of message passing for various graph neural network (GNN) architectures. The x-axis represents the number of layers (L), while the y-axis shows the Dirichlet energy (E). As the number of layers increases, traditional convolutional GNNs (GCN, GAT, GCNII, Res) suffer from over-smoothing, meaning that the Dirichlet energy decreases exponentially, and node representations become similar, hindering the ability to distinguish between nodes effectively. RUM, in contrast, exhibits significantly less over-smoothing, maintaining a higher Dirichlet energy across multiple layers, indicating better preservation of node differences.
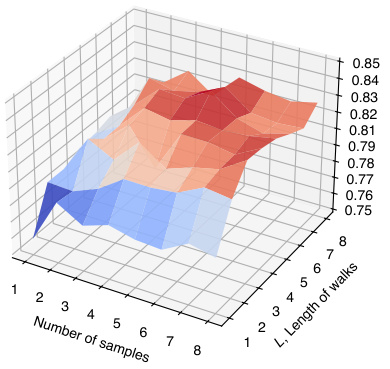
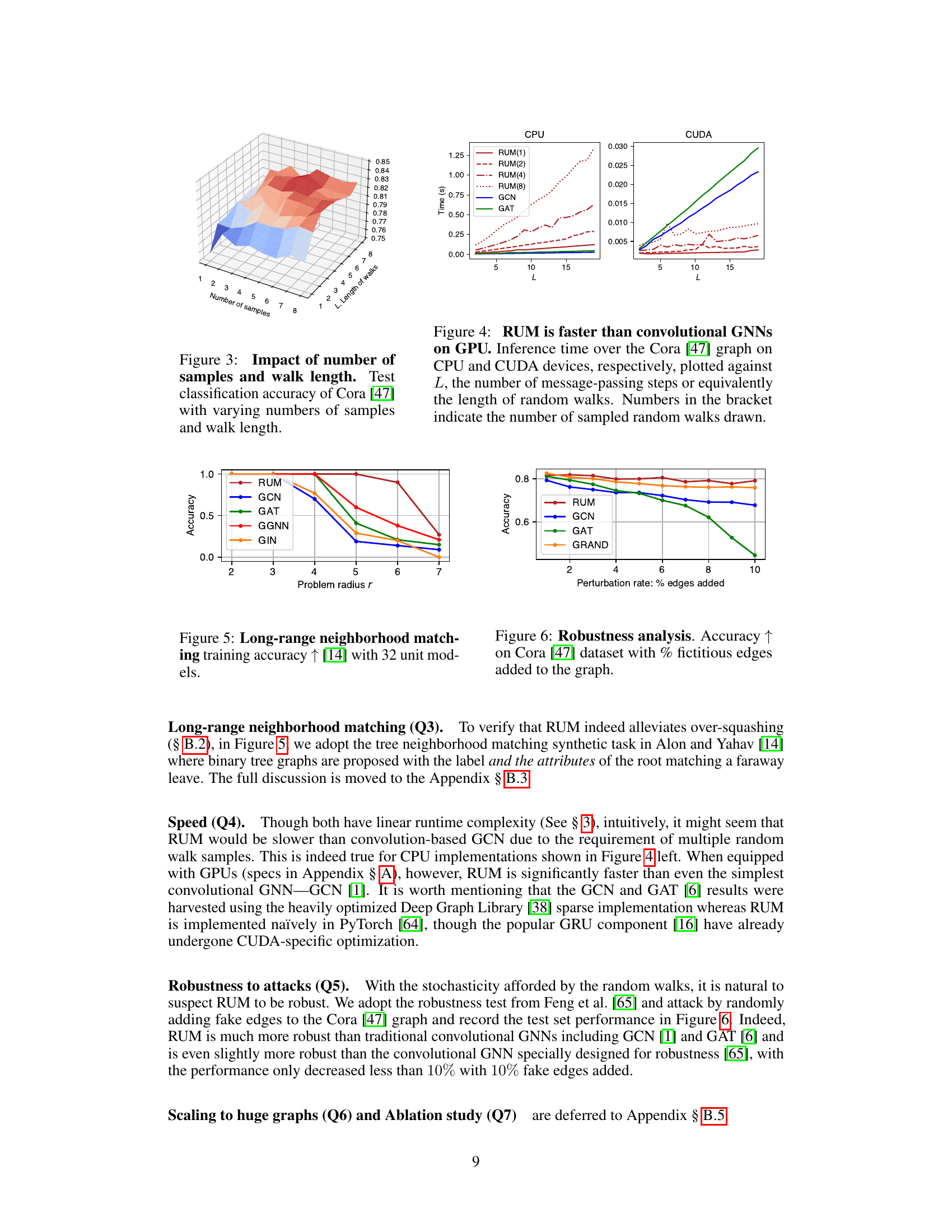
This figure shows a 3D surface plot illustrating the relationship between the number of samples used to estimate node representations, the length of random walks, and the resulting test classification accuracy on the Cora dataset. The x-axis represents the number of samples, the y-axis represents the length of random walks, and the z-axis represents the test accuracy. The plot reveals that increasing either the number of samples or the walk length generally improves the classification accuracy, up to a certain point where diminishing returns set in.
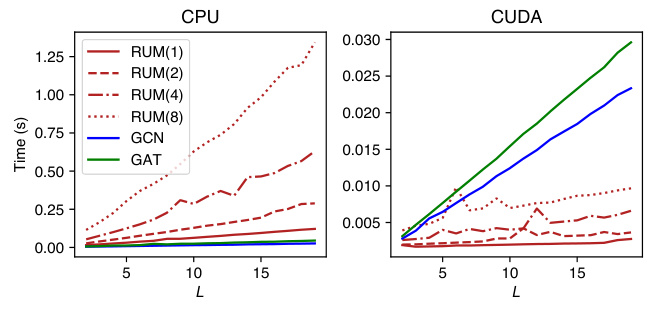
This figure compares the inference time of RUM with GCN and GAT on the Cora dataset. The x-axis represents the number of message-passing steps (L) or the length of random walks. The y-axis represents the inference time in seconds. The figure shows that RUM is faster than GCN and GAT, especially on GPU. The numbers in the bracket indicate the number of sampled random walks used for each RUM configuration.

The figure shows the accuracy of different Graph Neural Network (GNN) models on a long-range neighborhood matching task. The task involves predicting the label of a node based on its attributes and those of a node located far away in the graph. The x-axis represents the ‘problem radius,’ which is the distance between the nodes whose attributes need to be matched. The y-axis is the accuracy of the prediction. The results indicate that RUM outperforms other GNN models, especially when the problem radius is large, highlighting RUM’s ability to capture long-range dependencies.

This figure demonstrates the robustness of the RUM model against adversarial attacks. The x-axis represents the percentage of randomly added fictitious edges to the Cora graph, simulating noise or corruption in the graph structure. The y-axis shows the classification accuracy achieved by different GNN models (RUM, GCN, GAT, and GRAND). The plot visually shows how the accuracy of each model degrades as the level of perturbation increases. The RUM model exhibits higher robustness than the other GNNs, showing a smaller decrease in accuracy even with a high percentage of added edges.
More on tables
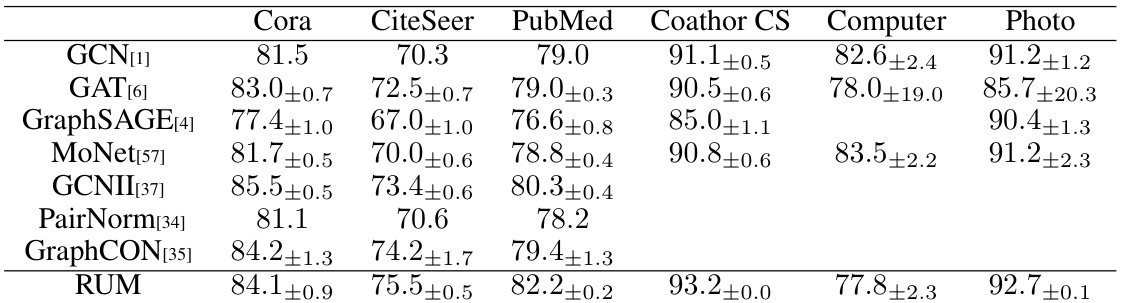
This table presents the test set accuracy and standard deviation for node classification task on several benchmark datasets. The results are shown for various Graph Neural Network (GNN) models, including GCN, GAT, GraphSAGE, MoNet, GCNII, PairNorm, GraphCON, and the proposed RUM model. The datasets include Cora, CiteSeer, PubMed, Coauthor CS, Computer, and Photo. The upward-pointing arrow (↑) indicates that higher values are better.
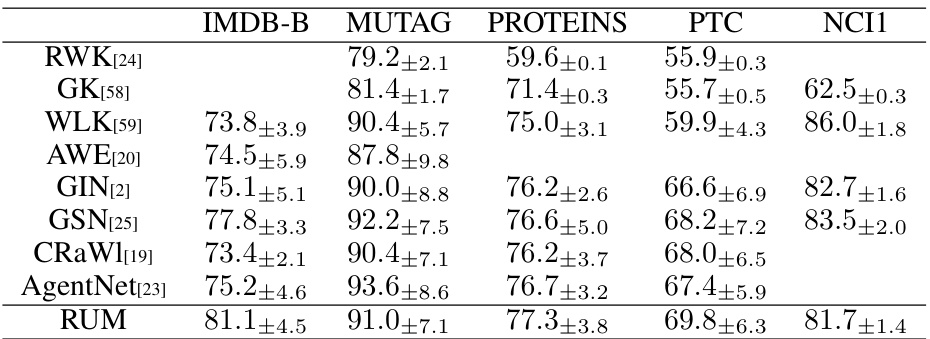
This table presents the results of binary graph classification experiments using various graph neural network models, including RUM. The accuracy is reported for several benchmark datasets (IMDB-B, MUTAG, PROTEINS, PTC, NCI1), comparing the performance of RUM against several other state-of-the-art methods. Higher accuracy indicates better performance.
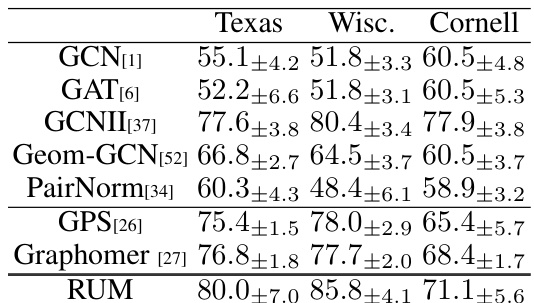
This table presents the results of node classification experiments on three heterophilic datasets: Texas, Wisconsin, and Cornell. The results compare the performance of various Graph Neural Network (GNN) architectures, including GCN, GAT, GCNII, Geom-GCN, PairNorm, GPS, Graphomer, and the proposed RUM model. Heterophilic datasets are challenging because of the presence of conflicting labels in the neighborhoods of nodes. The table shows the test accuracy and standard deviation for each model, indicating the relative performance and stability of different GNNs on these difficult datasets. RUM achieves the highest accuracy in two of three datasets and is comparable to the best-performing model on the remaining dataset.
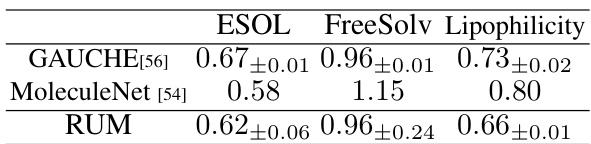
This table presents a comparison of the root mean squared error (RMSE) achieved by the RUM model and other state-of-the-art models on three graph regression tasks from the OGB and MoleculeNet benchmark datasets. Lower RMSE indicates better performance. The results show that RUM achieves competitive performance compared to the best models on these tasks.

This table presents the results of an ablation study conducted on the Cora dataset to evaluate the impact of different components of the RUM architecture on the model’s performance. The test set accuracy is reported for several variations, where either the topological representation (Wu), the semantic representation (Wx), the self-supervised regularization loss (Lself), or the consistency regularization loss (Lconsistency) have been removed from the RUM model. This allows for a quantitative analysis of each component’s contribution to the overall performance.

The table presents the test set accuracy and standard deviation for node classification on several benchmark datasets using various graph neural network models, including GCN, GAT, GraphSAGE, MoNet, GCNII, PairNorm, GraphCON, and RUM. The results show RUM achieves competitive or superior performance compared to other models.

This table presents the results of a graph isomorphism test using various Graph Neural Networks (GNNs) on the Circular Skip Link (CSL) dataset. The CSL dataset is specifically designed to be challenging for GNNs. The table shows that while most GNNs fail to perform better than a random baseline, indicating a failure to discriminate between the non-isomorphic graphs within this dataset, RUM, and 3WLGNN achieve significantly higher accuracy. This highlights RUM’s ability to discriminate between non-isomorphic graphs, a capability beyond most standard convolutional GNNs.
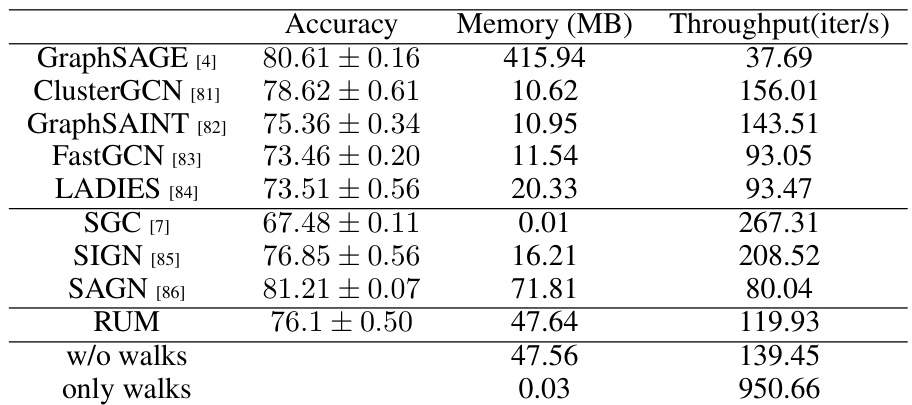
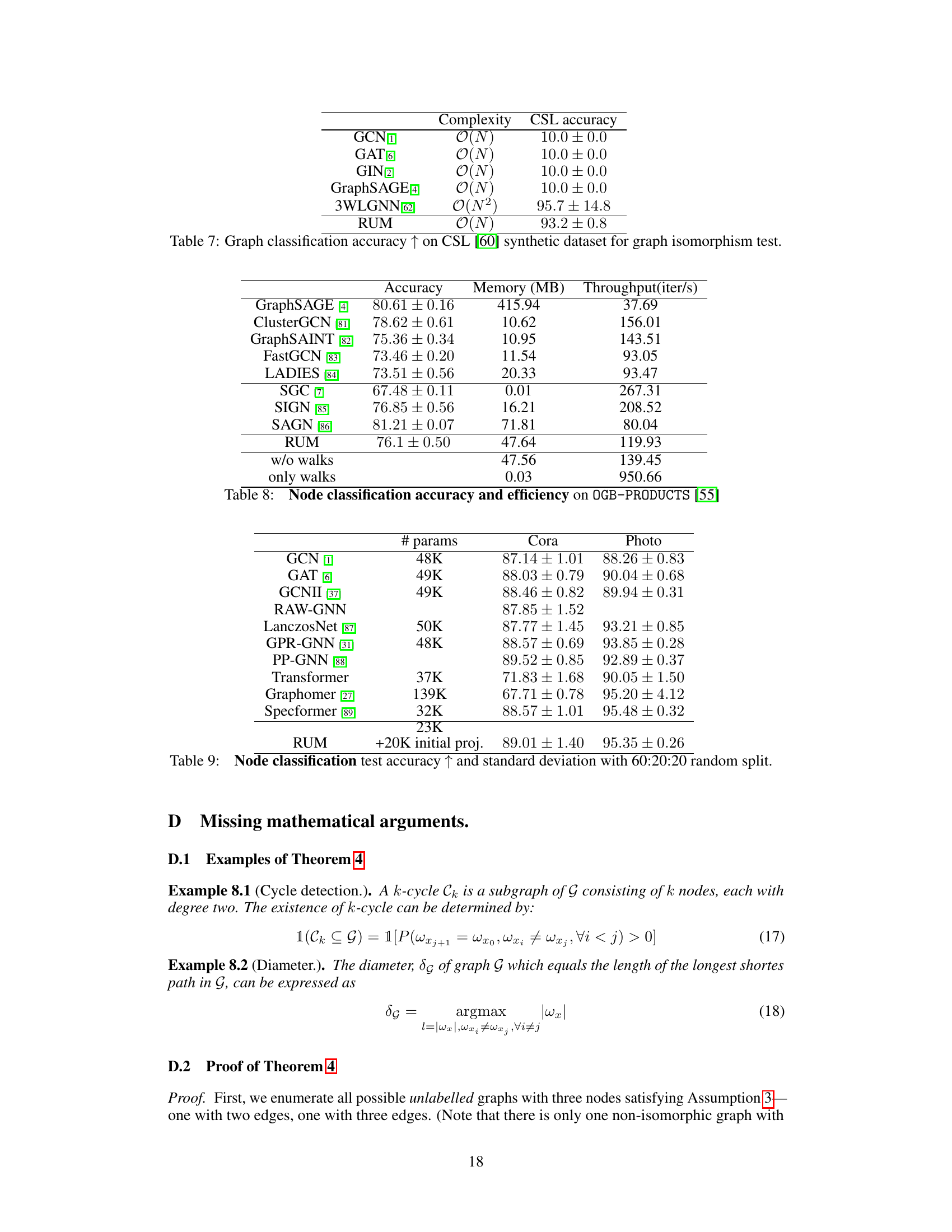
This table presents a comparison of the performance of several graph neural network (GNN) models, including RUM, on the OGB-PRODUCTS dataset, a large-scale benchmark dataset for graph classification. The metrics reported include accuracy, memory usage (in MB), and throughput (iterations per second). The table shows that RUM achieves comparable accuracy to other state-of-the-art GNNs while demonstrating significant improvements in memory efficiency and throughput.

This table presents a comparison of the test set accuracy achieved by various graph neural network models on node classification tasks, specifically on the Cora and Photo datasets. The accuracy is reported with standard deviation to show the variability. The table includes several state-of-the-art GNN models along with RUM (Random Walk with Unifying Memory) for comparison, highlighting RUM’s competitive performance.
Full paper#