Rethinking 3D Convolution in $ll_p$-norm Space

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it introduces a novel convolution method based on the l1-norm, addressing limitations of traditional methods in 3D data processing. This has significant implications for improving efficiency and reducing energy consumption in 3D CNNs, impacting applications like object recognition and scene understanding, which are vital in many fields.

Visual Insights

#

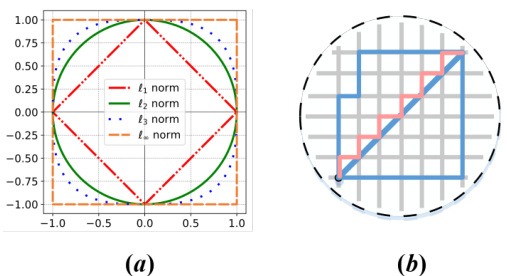
Figure 1(a) shows a visualization of the unit circles for different lp-norms (l1, l2, l3, and l∞). It illustrates how the shape of the unit circle changes as the value of p changes, reflecting the different ways these norms measure distance. Figure 1(b) provides a visual explanation of the Manhattan distance (l1-norm), showing how it calculates distance along the grid lines rather than the straight-line distance used in the Euclidean norm (l2-norm). The figures highlight the differences in how these norms treat distances and thus the diverse properties they offer in feature extraction and network training.

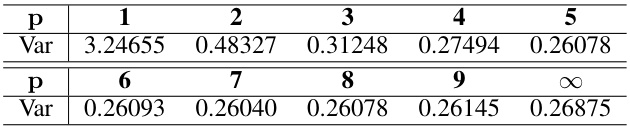
This table presents the variance of the lp-norm of a Gaussian random vector for different values of p (1, 2, 3, 4, 5, 6, 7, 8, 9, and infinity). The dimension of the vector is 9 (mn = 9). The variance is a measure of how spread out the distribution of the lp-norm is. This table is used to support the claim that the l1-norm is more robust to random noise than other lp-norms.

In-depth insights

#

lp-Norm Convolutions

#

The concept of “lp-Norm Convolutions” introduces a novel approach to feature extraction in convolutional neural networks by replacing the traditional inner product operation with an lp-norm distance calculation. This offers several potential advantages. The choice of p (the order of the norm) allows for tunability, influencing the network’s sensitivity to outliers and sparsity. For example, the l1-norm is robust to outliers and promotes sparsity, making it potentially more efficient and effective for certain types of data, such as point clouds. Conversely, the l2-norm retains a close relationship to traditional convolutions but provides a different perspective on feature extraction. However, the use of lp-norm convolutions introduces new computational challenges and may require customized optimization strategies to achieve comparable performance to traditional methods. Theoretical analysis, including the universal approximation theorem for lp-norm based networks, is essential to establish the validity and potential of this approach. Ultimately, the effectiveness of lp-norm convolutions depends on the specific application, dataset characteristics, and the choice of p. Careful empirical evaluation is necessary to determine its advantages and limitations.

Universal Approximation

#

The concept of “Universal Approximation” within the context of neural networks is a crucial one, asserting the theoretical capability of certain network architectures to approximate any continuous function to a desired level of accuracy. This property underpins the power and flexibility of neural networks, providing a strong theoretical foundation for their widespread applicability. The paper’s proof of the Universal Approximation Theorem for l_p-norm based convolutional networks is particularly significant, demonstrating that these networks, despite their non-traditional approach to convolution, still possess this critical property. This finding is important because it legitimizes the use of l_p-norm convolutions as a viable alternative to traditional methods, opening avenues for exploration of potentially more efficient and robust architectures. The specific focus on l₁-norm networks highlights their potential for efficient computation, owing to the inherent computational simplicity of addition operations compared to multiplications, often present in inner product-based convolution. The theorem’s proof, along with its implications for robustness and theoretical guarantees of convergence, strengthens the argument for adopting l₁-norm based convolutional neural networks, specifically in computationally constrained applications and tasks dealing with noisy or incomplete data, offering a solid theoretical basis for their practical implementation and use.

Optimization Strategies

#

The research paper explores optimization strategies crucial for effectively training networks using the L1-norm. The core challenge lies in the difficulty of directly applying standard gradient descent methods to L1-norm-based convolutions, which often leads to slow convergence and suboptimal results. To overcome this, the authors propose two novel strategies: a Mixed Gradient Strategy (MGS) and a Dynamic Learning Rate Controller (DLC). MGS cleverly combines the gradients of L1- and L2-norm networks, benefiting from the stability of L2 in the initial training stages while transitioning towards the sparsity-inducing properties of L1 as training progresses. DLC dynamically adjusts the learning rate, maintaining higher values initially to accelerate convergence and shifting to lower values later for fine-tuning. These combined strategies are shown to significantly enhance both training efficiency and model performance. A regret analysis is included to provide a theoretical guarantee for the convergence of their approach. This demonstrates a rigorous approach to the problem, making the proposed optimization methodology both innovative and well-founded.

3D Point Cloud Tasks

#

The application of 3D convolutional neural networks to point cloud data is a rapidly evolving field. Point clouds, inherently unstructured, present unique challenges for traditional convolutional architectures. This necessitates specialized methods for feature extraction and processing. The paper delves into the core operations, exploring alternatives to standard inner product-based convolutions. The focus on l_p-norm convolutions, particularly l₁-norm, offers interesting advantages: enhanced robustness to noisy data and potentially lower computational costs due to their reliance on addition rather than multiplication. The effectiveness of l₁-norm convolutions is further investigated through customized optimization strategies, highlighting the need for tailored training techniques to address challenges associated with non-smooth loss functions. Ultimately, the exploration of l_p-norm convolutions and their application to 3D point cloud tasks points to an exciting avenue of research, potentially resulting in more efficient and effective models.

Limitations and Future

#

A thoughtful analysis of the “Limitations and Future” section of a research paper would delve into the shortcomings of the current work and propose promising avenues for future research. Limitations might include the scope of the study (e.g., limited datasets, specific methodologies), the generalizability of findings to different contexts, or computational constraints. Future directions could expand upon these limitations by suggesting larger-scale experiments, investigating alternative approaches, exploring novel applications, and addressing methodological shortcomings. For example, limitations concerning dataset size could be addressed by future studies using more extensive and diverse datasets. It is important to discuss the feasibility of the proposed future work, and whether there are any potential challenges or limitations. A strong “Limitations and Future” section highlights both the present study’s limitations and the promising research paths that could build upon this work, enhancing its impact and contribution to the field.

More visual insights

#

More on figures

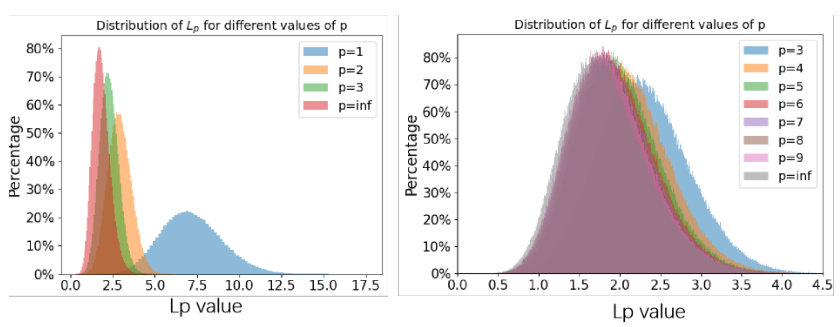
This figure visualizes the distribution of the lp-norm (||G||p) of a standard Gaussian vector G for different values of p. The left panel shows the distributions for p=1, 2, 3, and infinity, while the right panel focuses on p=3 to infinity, showing how the distribution changes as p increases. The dimension of the Gaussian vector G is 9 in both cases. This figure illustrates the impact of different lp-norms on the distribution of data, providing insights into their properties and behavior.

This figure compares the gradient magnitude of weights in each layer of the l₁-PointNet++ and the standard PointNet++ at the first iteration. The y-axis is in log scale, and it shows that the gradients from l₁-PointNet++ are much smaller than those from PointNet++. This difference in gradient magnitude is a key motivation for introducing the mixed gradient strategy (MGS) in the paper.

More on tables

This table presents a quantitative comparison of the performance of different 3D convolutional neural networks on the ShapeNet part segmentation task. The models compared include a traditional 3D CNN, an l1-norm based 3D CNN, PointNet, l1-norm based PointNet, PointNet++, and an l1-norm based PointNet++. The performance metric used is mean Intersection over Union (mIoU), calculated for each object part and averaged across all parts. The table also shows the number of shapes in the ShapeNet dataset for each category.

This table presents a comparison of the performance of different models on the task of semantic segmentation in scenes using the S3DIS dataset. It shows the mean Intersection over Union (IoU), overall accuracy, and energy consumption for PointNet, l₁-PointNet, PointNet++, and l₁-PointNet++. The results indicate that the proposed l₁-norm based methods achieve competitive performance compared to traditional methods, while consuming significantly less energy.

This table presents a quantitative comparison of the garment pose estimation performance between the original GarmentNets model and the proposed l1-GarmentNets model. The evaluation metric used is the Chamfer distance, which measures the average distance between corresponding points on the predicted and ground truth garment meshes. Lower Chamfer distance values indicate better pose estimation accuracy. The results are broken down by garment type (Dress, Jumpsuit, Skirt, Top, Pants, Shirt).

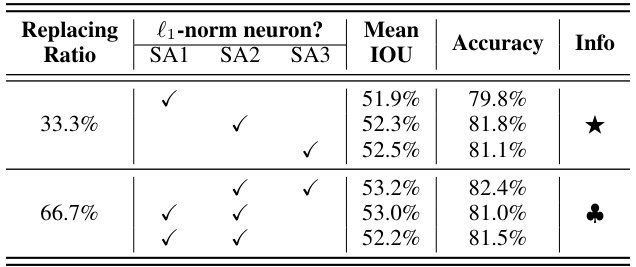
This table presents the ablation study of replacing different ratios of the original PointNet++ modules with the proposed l1-norm based modules. It shows the impact of replacing different proportions of PointNet++’s SetAbstraction (SA) modules with the l1-norm-based counterparts on the mean Intersection over Union (IOU) and accuracy, along with the estimated energy consumption. The results indicate that a higher replacement ratio (66.7%) generally leads to better performance, suggesting the effectiveness of the l1-norm approach in enhancing feature extraction.

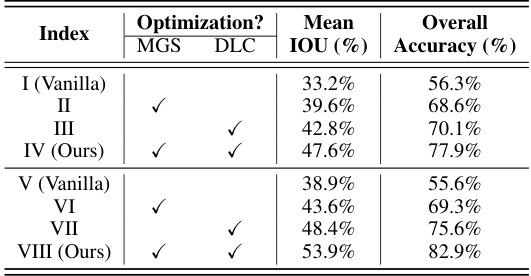
This table presents the ablation study results on the S3DIS dataset using different variants of l1-Nets. It compares the performance of the l1-PointNet and l1-PointNet++ models with and without the proposed Mixed Gradient Strategy (MGS) and Dynamic Learning Rate Controller (DLC). The ‘Vanilla’ rows show results without any of the proposed optimization strategies. The table shows that the use of both MGS and DLC leads to improved performance. This demonstrates the effectiveness of the proposed optimization strategies in enhancing the performance of l1-norm based convolutional neural networks.

Full paper

#