↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Modern neural networks are computationally expensive. Structured pruning, removing entire parts of the network, is an effective technique to improve efficiency. However, existing methods often lack theoretical grounding and require manual threshold tuning which limits their performance. This creates a need for a more principled approach.
This paper presents BMRS, a novel Bayesian method for structured pruning. BMRS leverages recent advancements in Bayesian structured pruning with multiplicative noise and Bayesian model reduction for efficient model comparison. The authors demonstrate that two versions of BMRS, one based on a truncated log-normal prior and another on a truncated log-uniform prior, provide reliable compression and accuracy without threshold tuning while achieving a better performance-efficiency trade-off compared to existing methods on multiple datasets and network architectures.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel Bayesian method for structured neural network pruning, addressing the critical need for efficient and accurate model compression. The method offers a principled approach, avoiding the need for threshold tuning and achieving competitive performance. This work is timely, given the increasing focus on model efficiency and sustainability in AI research. It opens avenues for further research in Bayesian pruning techniques and efficient model compression strategies.
Visual Insights#

This figure illustrates the Bayesian Model Reduction for Structured Pruning (BMRS) method. The left panel shows a histogram of the expected values of noise variables (E[θ]) from the original model, highlighting the distribution before pruning. The middle panel displays the original and reduced priors for the noise variables. The reduced prior is designed to shrink the noise variable values toward zero, inducing sparsity. The difference in log-evidence (ΔF) between these two priors is then calculated. The right panel displays the histogram of E[θ] after pruning, indicating how the noise variable distribution changes after pruning based on the ΔF calculation. BMRS prunes structures based on if ΔF is greater than zero, indicating a significant improvement in the model’s log-evidence by removing the structure.
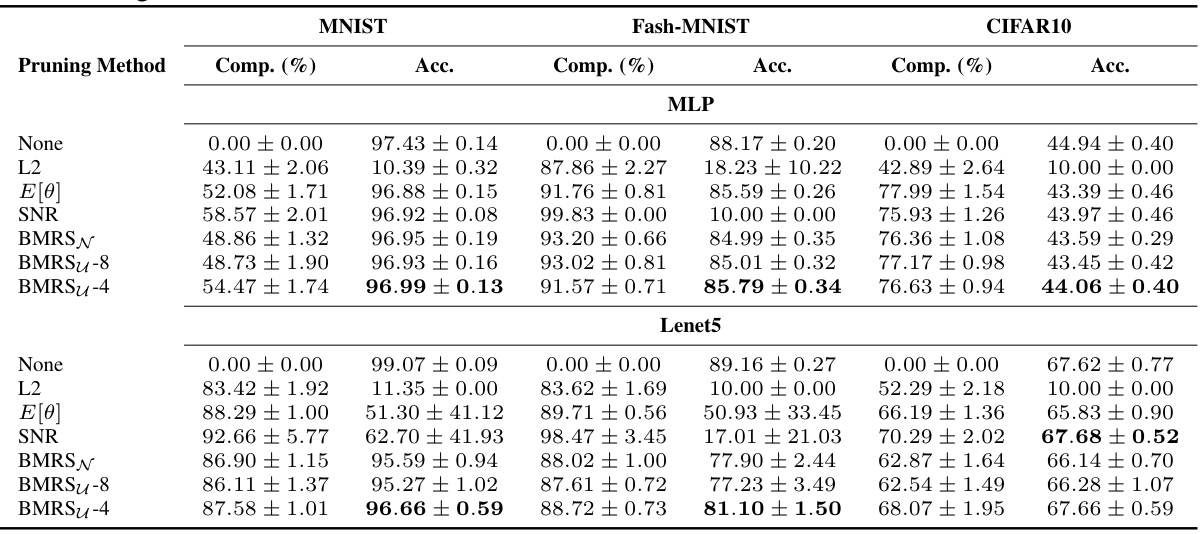
This table presents a comparison of the performance of different pruning methods across various datasets and neural network architectures. The methods compared include L2, E[θ], SNR, BMRSN, and two variants of BMRSu. For each method and dataset, the table reports the compression rate achieved (%) and the corresponding accuracy. The best accuracy for each compression rate is highlighted in bold. The results showcase the effectiveness of the proposed BMRS method in achieving high compression rates while maintaining competitive accuracy compared to other state-of-the-art pruning methods.
In-depth insights#
Bayesian Pruning#
Bayesian pruning is a powerful technique for improving the efficiency and performance of neural networks by strategically removing less important connections. It leverages Bayesian inference to estimate the probability of each weight or neuron being relevant to the model’s predictive ability. Weights or neurons with low probabilities are pruned, resulting in a smaller, faster, and often more accurate model. Unlike traditional pruning methods that rely on heuristics or approximations, Bayesian pruning provides a principled framework for model reduction, effectively balancing accuracy and sparsity. This approach is particularly valuable for structured pruning, where entire groups of neurons or filters are removed, leading to significant computational savings. Various Bayesian methods, such as those employing spike-and-slab priors or multiplicative noise, are used to achieve this goal. A key advantage is the ability to determine optimal pruning thresholds automatically, avoiding the need for hyperparameter tuning, as opposed to threshold-based methods. Overall, Bayesian pruning offers a compelling solution for resource-constrained applications, potentially outperforming traditional techniques in accuracy while reducing model size and computational needs.
BMRS Algorithm#
The BMRS algorithm presents a novel Bayesian approach to structured neural network pruning. It leverages Bayesian Model Reduction (BMR) for efficient model comparison, enabling principled pruning decisions without relying on arbitrary thresholds. The algorithm incorporates multiplicative noise, allowing flexible sparsity induction at various structural levels (e.g., neurons or filters). Two versions are detailed, BMRSN using a truncated log-normal prior and BMRSu using a truncated log-uniform prior, offering distinct compression characteristics. BMRSN provides reliable compression without hyperparameter tuning, while BMRSu allows for more aggressive compression via tunable precision. The results demonstrate that BMRS offers a competitive performance-efficiency trade-off, achieving high compression rates while maintaining accuracy across various network architectures and datasets.
Prior Selection#
Prior selection is crucial in Bayesian structured pruning, significantly impacting the effectiveness of the pruning process. A poorly chosen prior can lead to suboptimal pruning decisions, hindering model compression and accuracy. The paper explores two distinct priors: the truncated log-normal and the truncated log-uniform. The truncated log-normal prior offers a reliable balance between compression rate and accuracy, requiring no threshold tuning, which simplifies the process. In contrast, the truncated log-uniform prior allows for more aggressive compression but necessitates tuning a threshold parameter, thus increasing complexity. This trade-off highlights the need for careful prior selection tailored to specific needs; prior selection is not a one-size-fits-all process. Ultimately, the choice hinges on the desired balance between compression efficiency and the computational cost of tuning hyperparameters. The paper’s investigation of these contrasting priors provides valuable insights into the implications of prior selection in Bayesian structured pruning.
Compression Rate#
The concept of ‘Compression Rate’ in the context of neural network pruning is crucial for evaluating the efficiency of model reduction techniques. A high compression rate indicates a significant reduction in model size and computational cost, which are essential for deploying models on resource-constrained devices or for reducing energy consumption. The paper’s focus on achieving high compression rates without sacrificing accuracy is a major contribution. However, the optimal compression rate is not a fixed value; it depends on a trade-off between model size and accuracy. The method presented allows for tuning the compression rate by adjusting hyperparameters, allowing researchers to tailor the tradeoff to their specific needs. This flexibility is important because overly aggressive pruning can harm performance, while insufficient pruning fails to provide substantial benefits. A key point of the research is the exploration of different prior distributions to control compression rate, demonstrating how choosing the right prior is crucial for balancing accuracy and model efficiency. The presented analysis shows that the proposed Bayesian methods offer a competitive trade-off compared to other methods, showcasing the value of a principled approach using Bayesian model reduction for achieving the desired level of model compression.
Future Work#
The paper’s omission of a dedicated ‘Future Work’ section presents an opportunity for insightful expansion. Extending BMRS to handle more complex neural network structures beyond convolutional filters and fully connected layers would significantly broaden its applicability. This could involve exploring its effectiveness with transformer architectures or recurrent neural networks. Investigating alternative sparsity-inducing priors within the BMRS framework, beyond the log-normal and log-uniform distributions, is another promising avenue. A more in-depth analysis of the relationship between compression rate, model accuracy, and the choice of priors (especially for BMRSu with its tunable parameter) would enhance the understanding and optimization of the algorithm. Finally, thorough benchmarking against a wider range of state-of-the-art pruning techniques, on diverse datasets and network architectures, would solidify BMRS’s position within the broader context of neural network efficiency research. The theoretical grounding provided by BMRS makes it a suitable foundation for future investigations, particularly if accompanied by further rigorous empirical evaluation.
More visual insights#
More on figures

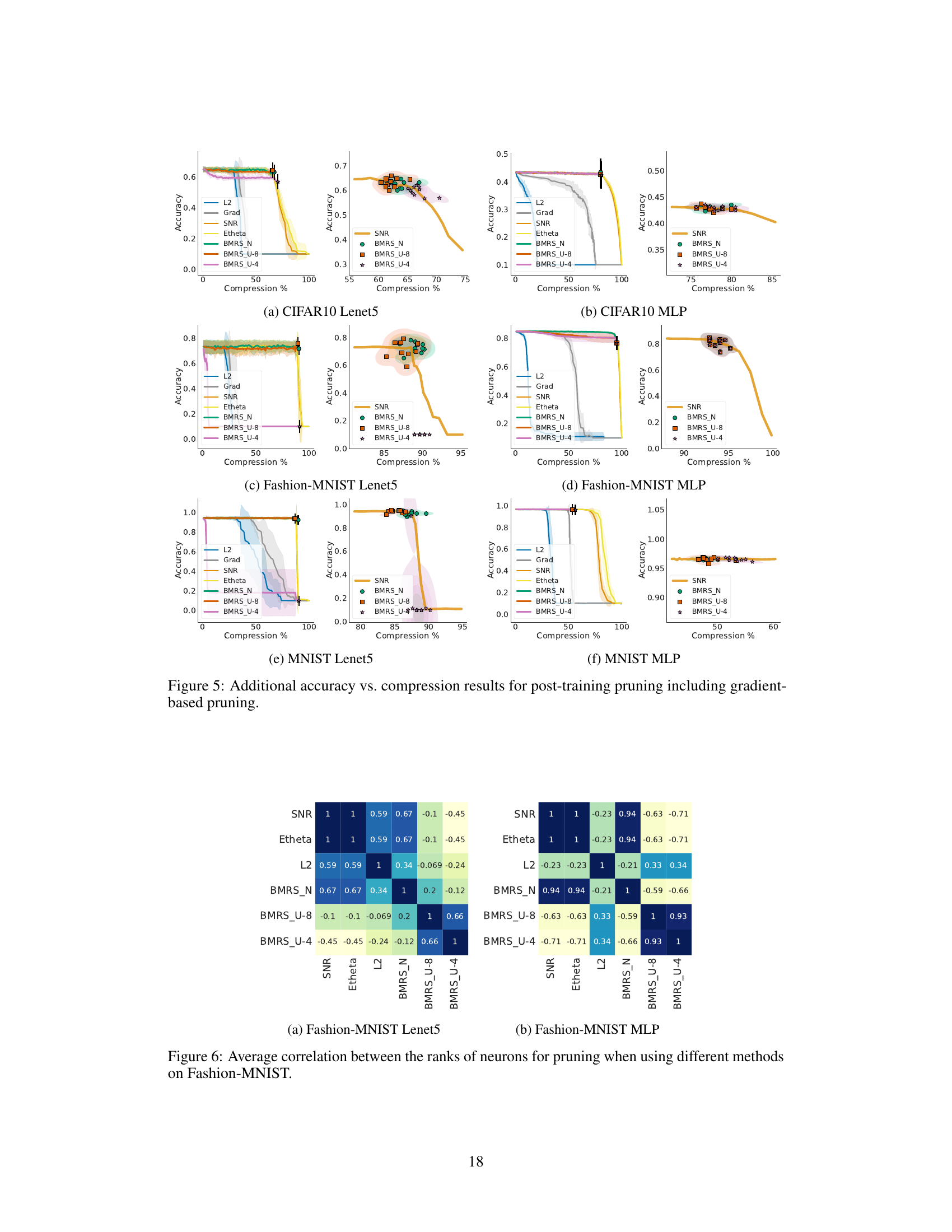
This figure compares the performance of different pruning methods (L2, SNR, BMRSN, BMRSu) on three datasets (CIFAR10, Fashion-MNIST, MNIST) using two network architectures (Lenet5, MLP). The left plots show accuracy versus compression rate curves, highlighting the trade-off between accuracy and model size. The right plots provide a detailed view of BMRS’s performance near the ‘knee’ point of the accuracy-compression curve, demonstrating its effectiveness in finding a good balance between these two factors. Shading represents the standard deviation across multiple runs. BMRS methods consistently stop at the knee point, indicating a good trade-off between accuracy and compression.

This figure displays the results of post-training pruning experiments on three datasets: CIFAR10, Fashion-MNIST, and MNIST, using various pruning methods including L2, SNR, Etheta, BMRSN, and BMRSu. The left plots show accuracy against compression percentage for each method, with error bars representing standard deviation over 10 random seeds. The BMRS methods’ maximum compression is indicated by the point where ΔF ≤ 0. The right plots provide a more detailed view comparing BMRS’s performance to SNR, using scatter plots and kernel density estimations to highlight the accuracy at maximum compression. The results indicate that BMRS methods consistently stop pruning near the optimal trade-off point (knee point of the accuracy vs. compression curve).
This figure compares the performance of various pruning methods (L2, SNR, E[θ], BMRSN, BMRSu-8, BMRSu-4) on three datasets (CIFAR10, Fashion-MNIST, MNIST) using a LeNet5 CNN and an MLP. The left plots show the accuracy vs. compression rate curves for each method across 10 different random seeds. Shading represents the standard deviation. For the Bayesian methods (BMRS), pruning stops when the change in log-evidence (∆F) becomes negative. The right plots provide a closer view, showing a scatter plot and kernel density estimation of the accuracy at maximum compression for BMRS against the SNR method. The results demonstrate that BMRS methods reliably stop pruning near the optimal point (Pareto front) on the accuracy-compression trade-off curve without needing any threshold tuning, unlike the other methods.
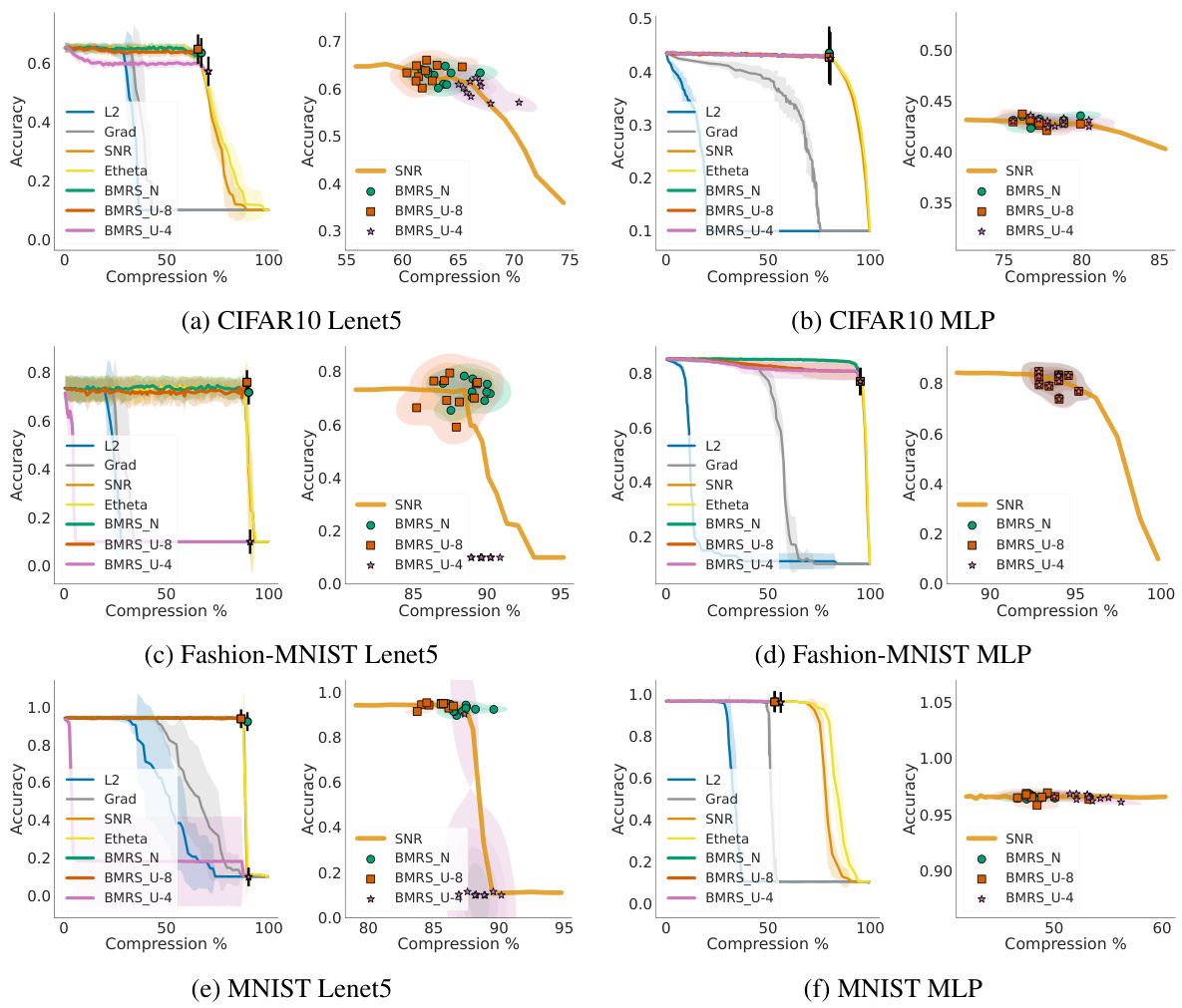
This figure compares different pruning methods (L2, Grad, SNR, Etheta, BMRSN, BMRSu-8, BMRSu-4) for three datasets (CIFAR10, Fashion-MNIST, MNIST) with two network architectures (Lenet5, MLP). The left plots show the accuracy versus compression rate for each method. Shading represents standard deviation across 10 random seeds. BMRS methods are marked at the maximum compression point where ΔF >0. The right plots show scatter plots and density estimations of accuracy at maximum compression for BMRS and SNR, highlighting that BMRS methods tend to stop near the optimal trade-off point (knee of the curve).
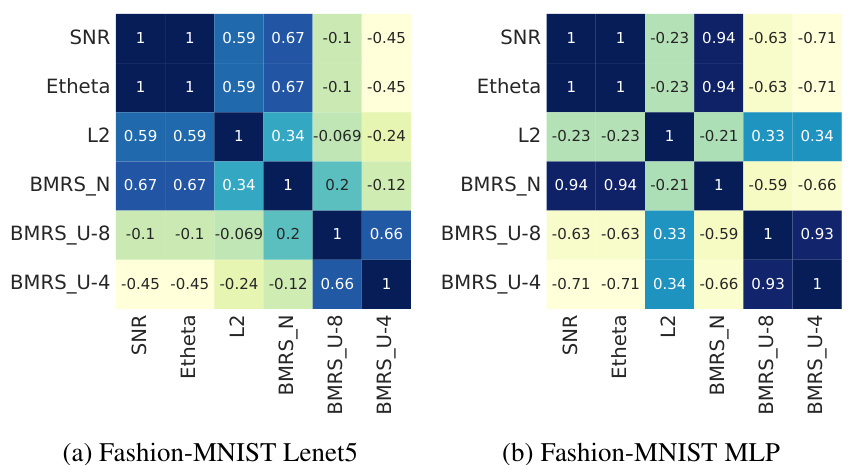
This figure presents the results of post-training pruning experiments on three datasets (CIFAR10, Fashion-MNIST, and MNIST) using various methods. The left-hand plots show accuracy against compression rate for each method (L2, SNR, Etheta, BMRSN, BMRSU-8, and BMRSU-4), illustrating the trade-off between model size and accuracy. The right-hand plots provide a closer look at the performance of BMRS methods, comparing their accuracy and compression rate to SNR. These plots highlight that BMRS methods tend to stop pruning near the optimal point (the ‘knee’ of the accuracy-compression curve), which is considered a preferred trade-off between model size and accuracy, demonstrating BMRS’s effectiveness in finding a good balance between compression and performance.

This figure shows the results of post-training pruning experiments on three datasets: CIFAR10, Fashion-MNIST, and MNIST, using different pruning methods. The left plots show accuracy vs. compression rate across ten random seeds, highlighting the performance of BMRS methods (BMRSN and BMRSu). The right plots provide scatter and density plots comparing the accuracy at the maximum compression rate of BMRS methods against the accuracy of SNR pruning at the knee point of the accuracy-compression curve. The results indicate that BMRS consistently stops pruning near the optimal balance of accuracy and compression, unlike other methods.
More on tables
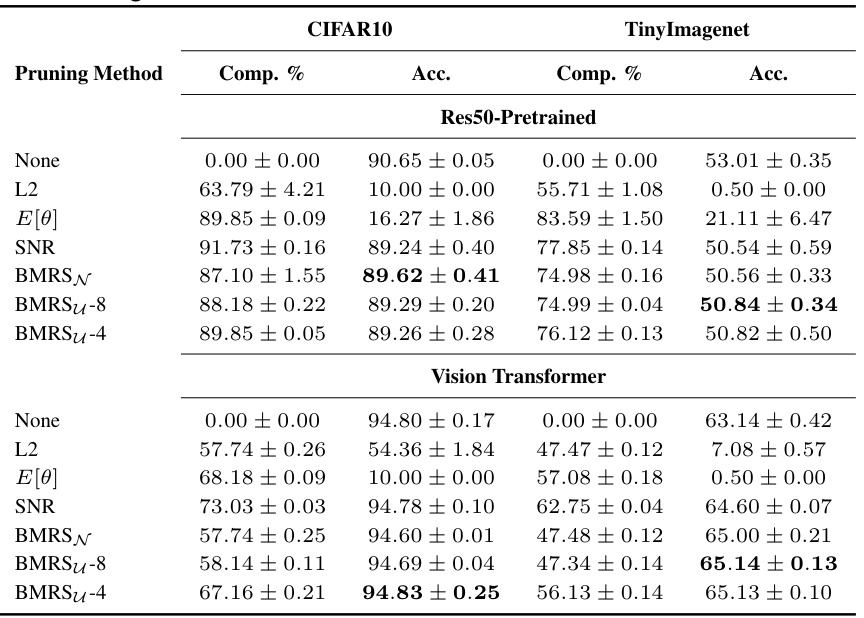
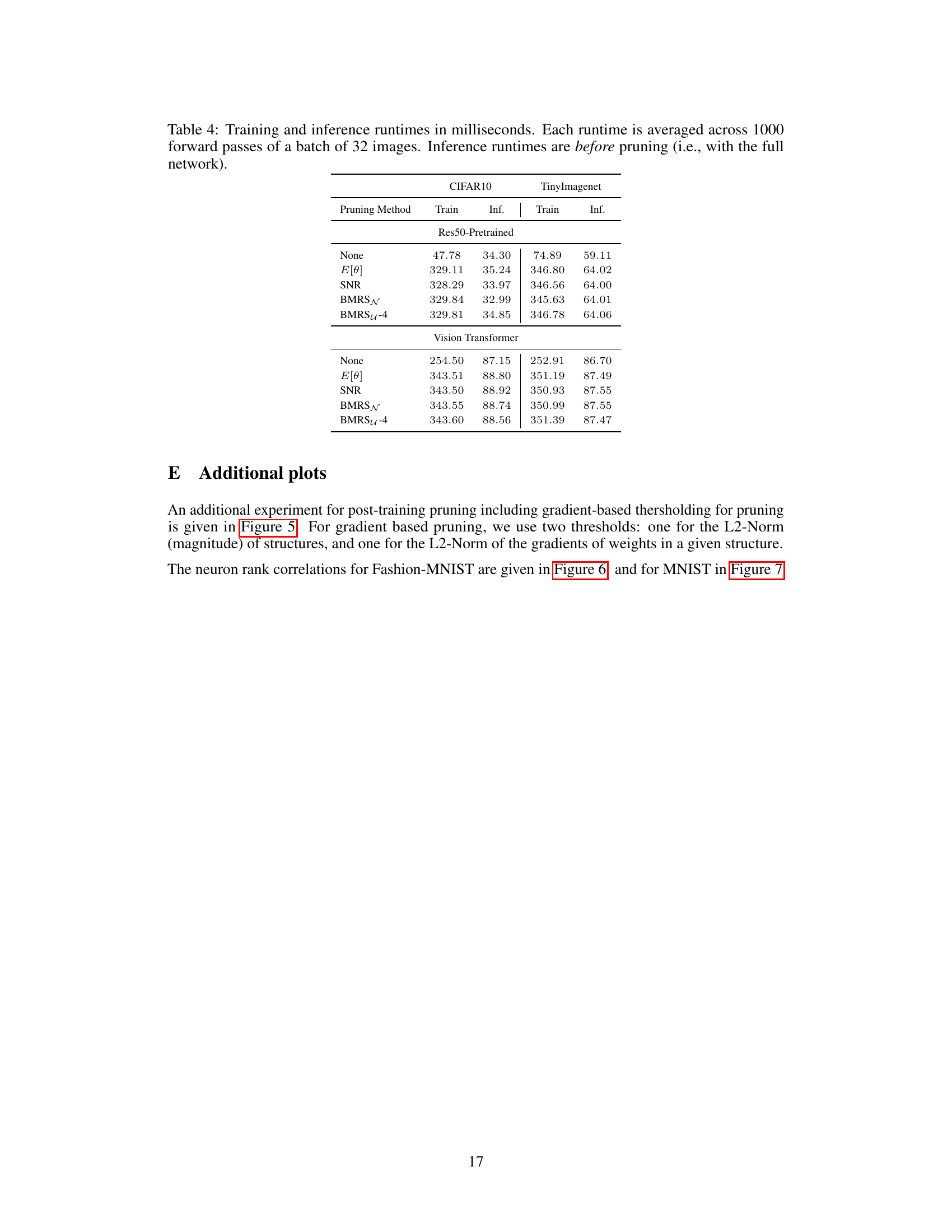
This table presents the results of experiments on CIFAR10 and TinyImagenet datasets using different pruning methods. The table shows the compression percentage and accuracy achieved by each method, including baselines like L2, E[θ], SNR, and the proposed BMRS and its variants (BMRSN, BMRSU-8, BMRSU-4). The best accuracy for each compression rate is highlighted in bold. This table allows for a comparison of the performance-efficiency trade-off of various pruning methods.
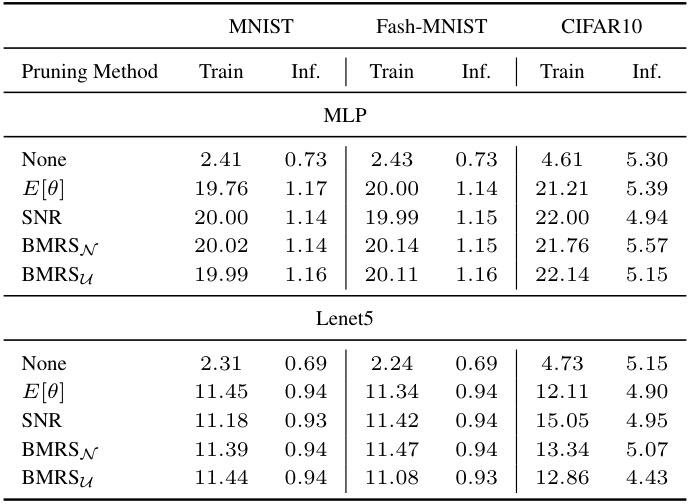
This table presents the performance comparison of different pruning methods on three datasets (MNIST, Fashion-MNIST, CIFAR10) using two neural network architectures (MLP and Lenet5). The table shows the compression rate achieved by each method and the corresponding accuracy. The best accuracy for each compression level is highlighted in bold. The methods compared include L2 norm pruning, pruning based on the expected value of noise variables (E[θ]), pruning based on signal-to-noise ratio (SNR), and the two proposed methods: BMRSN and BMRSu (with two different levels of precision).

This table presents the compression rates and accuracies achieved by different pruning methods on the CIFAR10 and TinyImagenet datasets using two different model architectures: Resnet50-pretrained and Vision Transformer. The methods compared include baseline methods (None, L2, E[θ], SNR) and the proposed BMRS methods (BMRSN, BMRSU-8, BMRSU-4). The best accuracy for each compression rate is highlighted in bold. This allows for a direct comparison of the performance and efficiency trade-offs of different pruning techniques.
Full paper#