↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
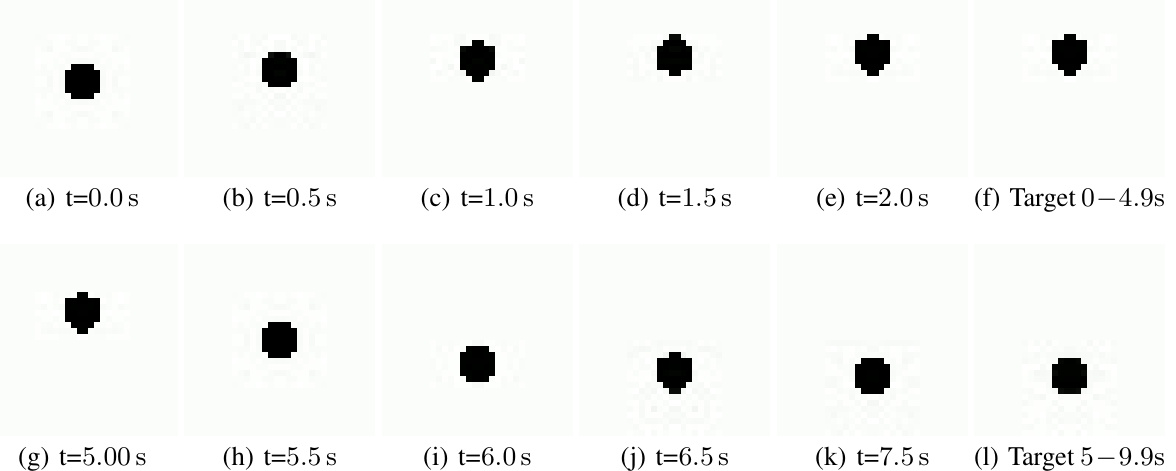
Controlling physical systems using data from high-dimensional sensors (e.g., images) is difficult. Existing latent-space control methods often lack mathematical structure, stability guarantees, and invertible input-output mappings. This hinders combining them with powerful model-based control strategies.
The paper introduces a novel method that uses a Coupled Oscillator Network (CON) to learn latent dynamics and implement model-based control. CON boasts inherent Input-to-State stability, efficient dynamics integration (using an approximate closed-form solution), and an invertible input-output mapping. This combination allows for effective and precise latent-space control, as demonstrated by high-quality performance on a soft robot using only raw image feedback.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to latent-space control, a critical challenge in robotics and AI. The Input-to-State Stable Coupled Oscillator Network (CON) model offers a mathematically rigorous and highly efficient solution, enabling high-quality performance in complex, high-dimensional environments. Its potential impact extends to various applications requiring control of systems based on high-dimensional sensory data.
Visual Insights#
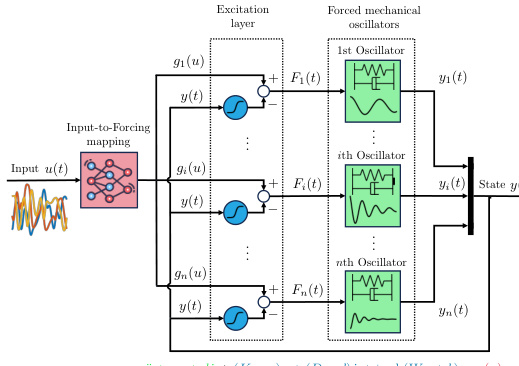
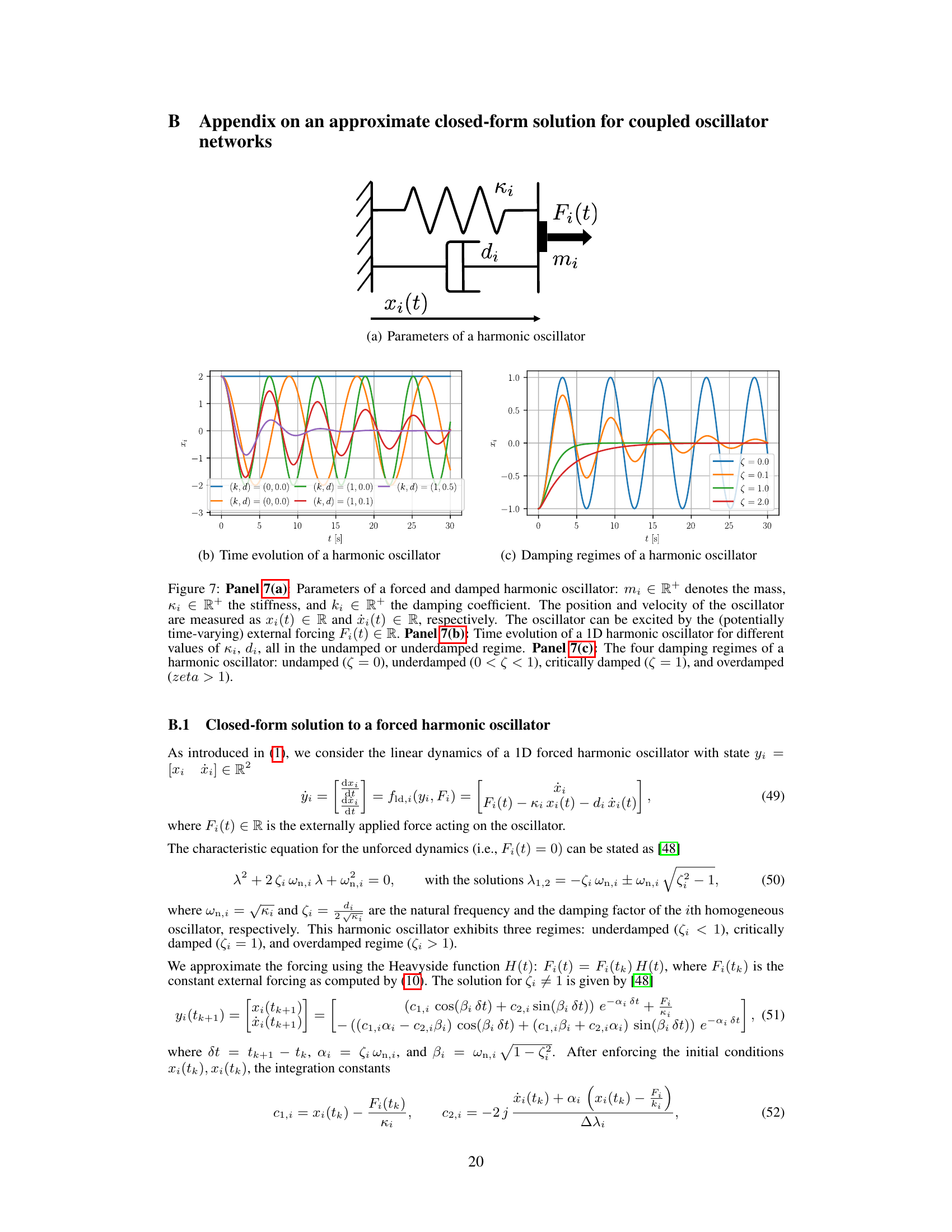
This figure illustrates the proposed Coupled Oscillator Network (CON) architecture. Panel (a) shows the CON’s internal structure: a network of coupled damped harmonic oscillators whose dynamics are influenced by an input u(t) via a mapping g(u) and by nonlinear coupling. Panel (b) shows how the CON is used for learning latent-space dynamics from image pixels. The initial observation and the input are encoded into a latent space. The CON predicts future states in the latent space based on the encoded input, which are then decoded to reconstruct the input and predict future observations.

This table compares the performance of the proposed Coupled Oscillator Network (CON) and its closed-form approximation (CFA-CON) against several baseline methods for learning latent dynamics from different datasets. The datasets include both simple unactuated mechanical systems (mass-spring, pendulum) and more complex actuated soft robots with varying degrees of freedom. The table shows the root mean squared error (RMSE) achieved by each model on each dataset, highlighting the effectiveness of the CON models, especially when dealing with the complexity of soft robot dynamics.
In-depth insights#
Latent Space Control#
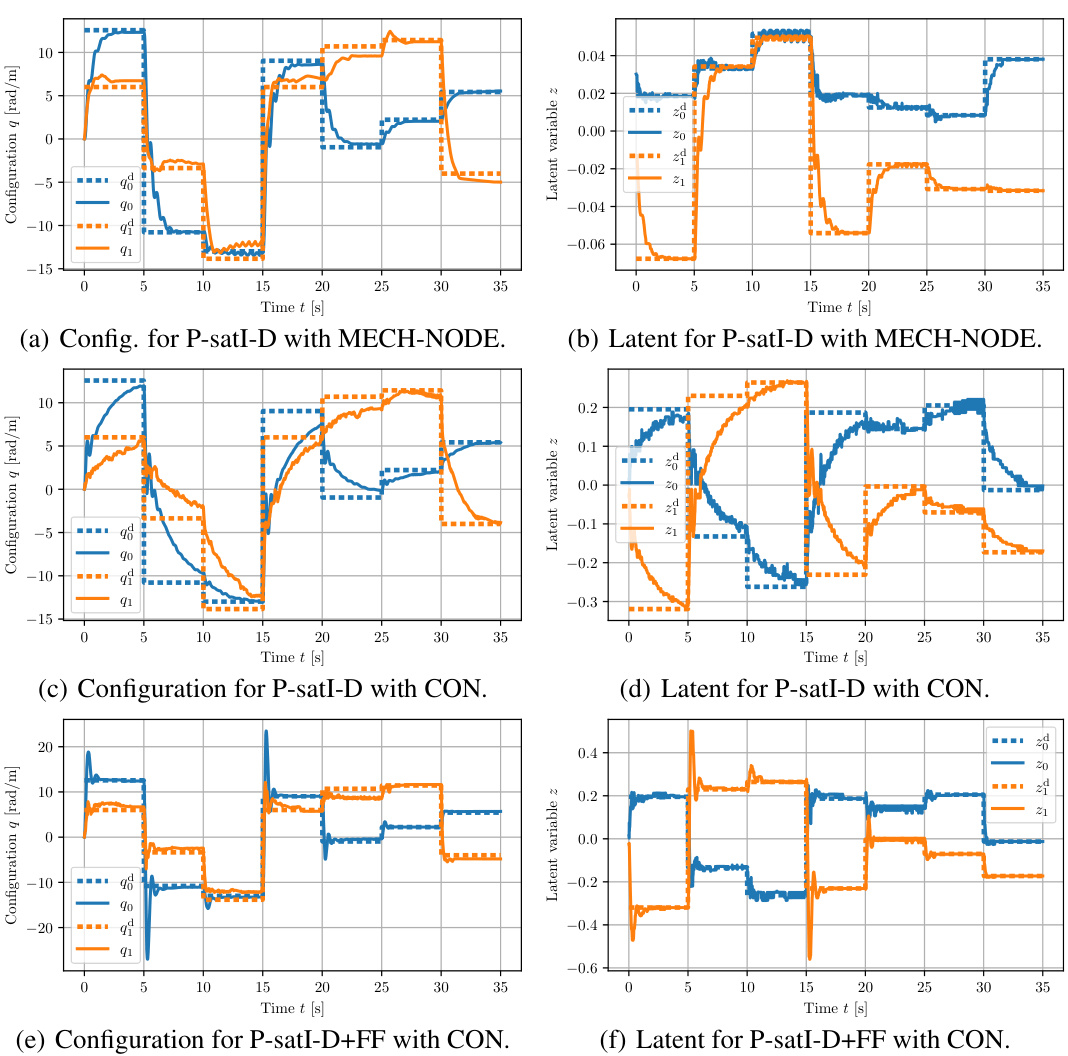
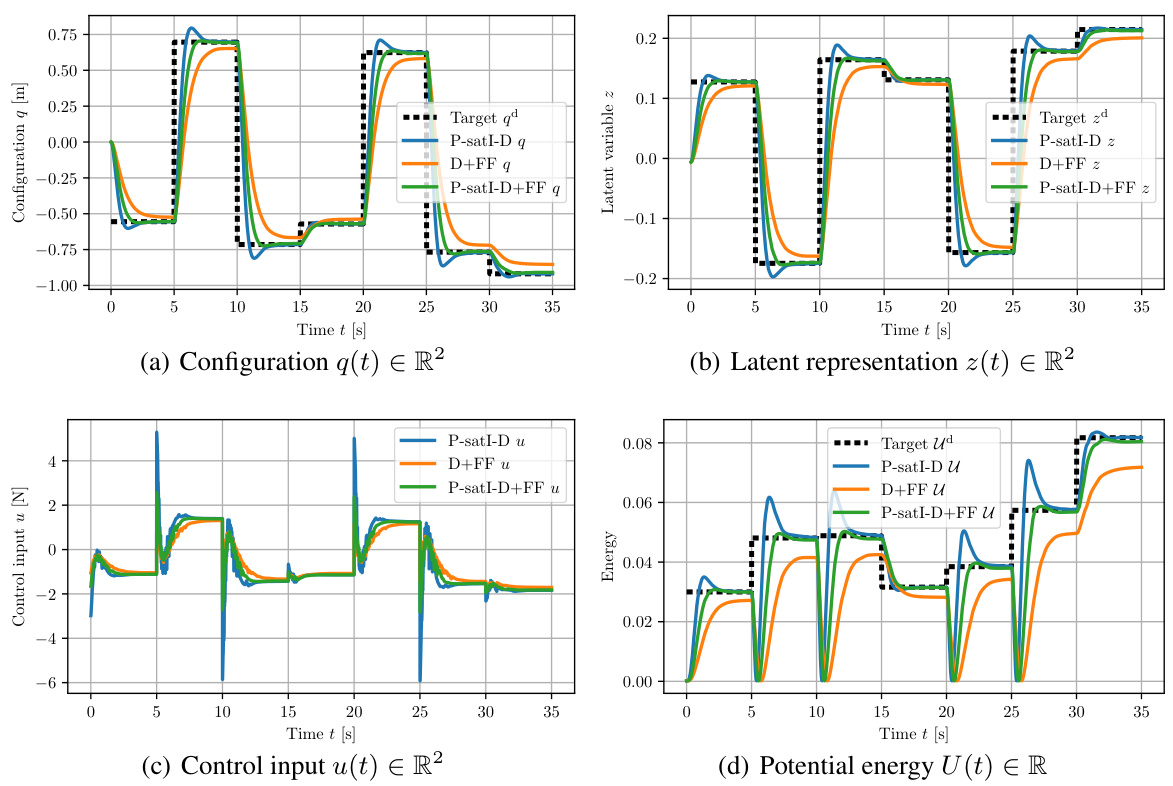
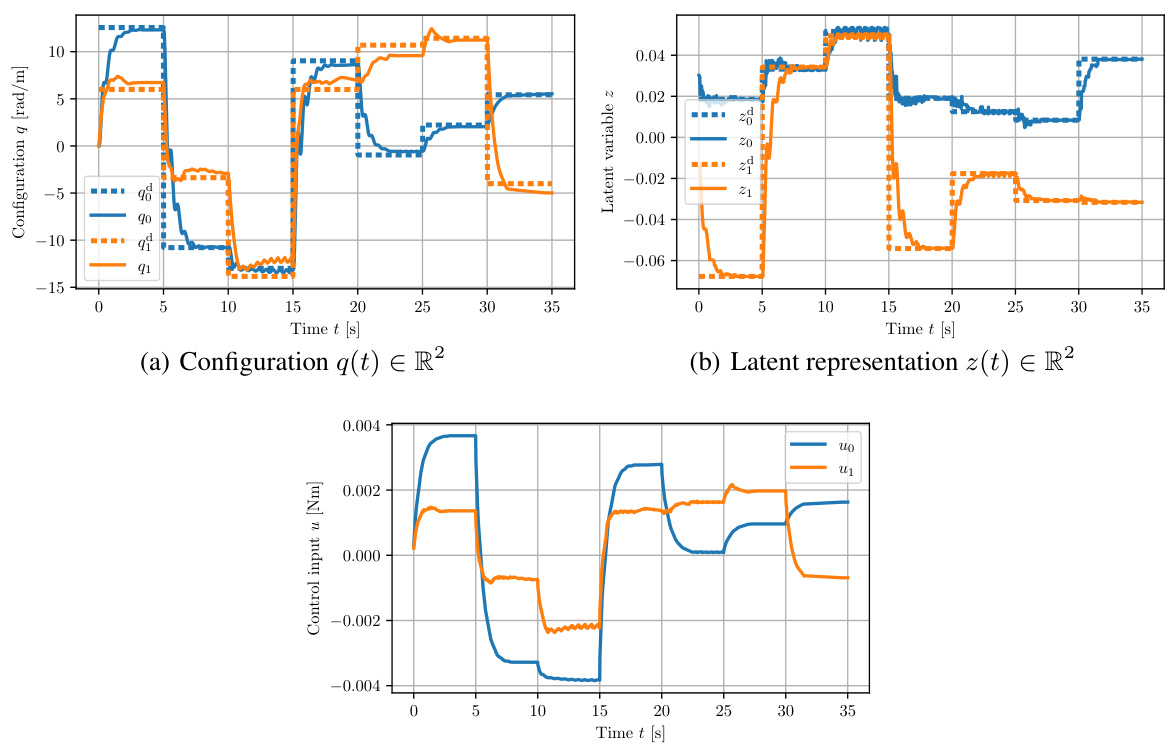
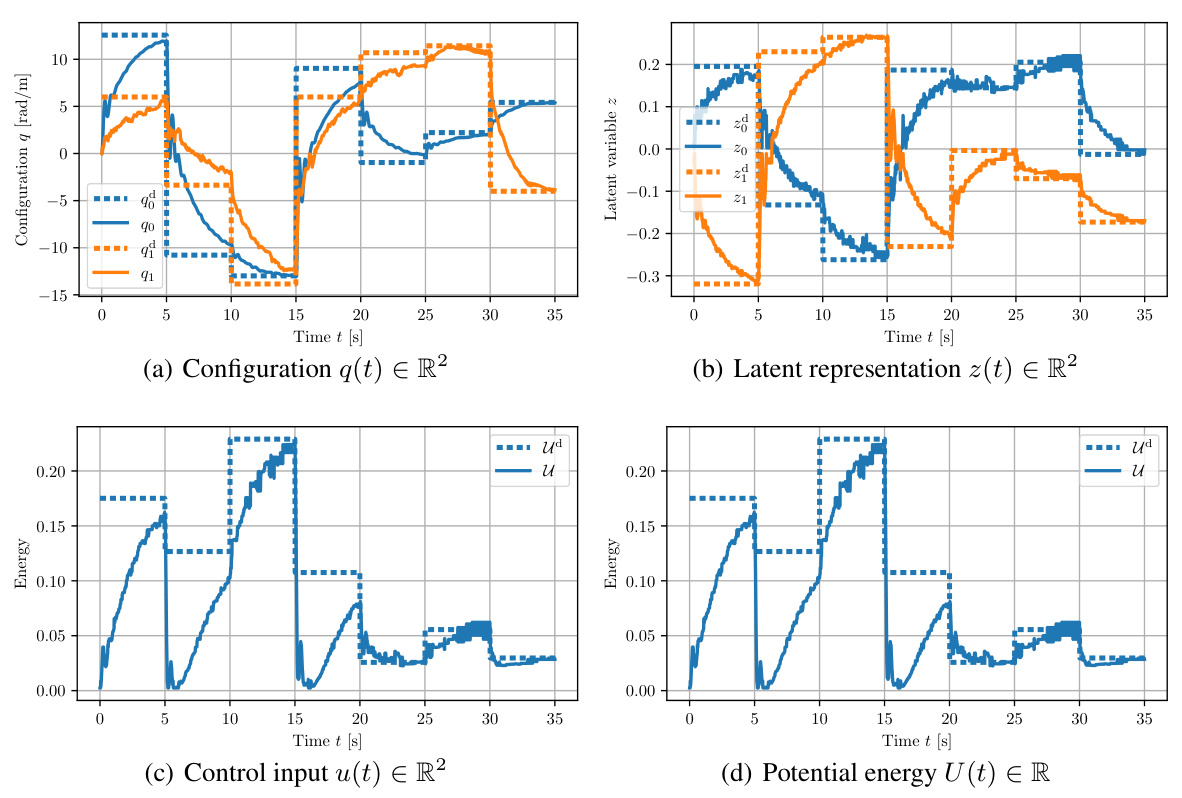
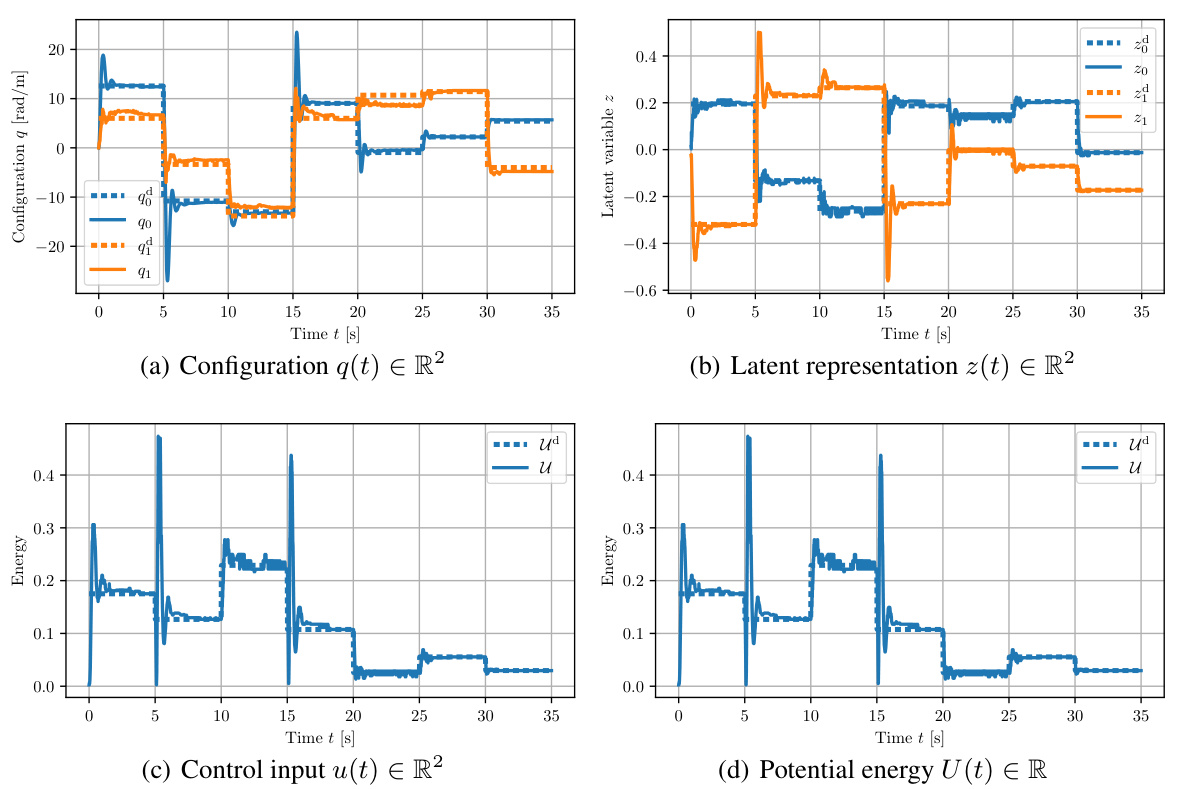
The concept of ‘Latent Space Control’ in the context of robotics and AI involves using a lower-dimensional representation (latent space) of high-dimensional sensory data (like images) to control a physical system. This approach is advantageous as it reduces computational complexity and enables learning from raw sensory inputs directly, bypassing the need for explicit state estimation. The paper focuses on developing a novel Coupled Oscillator Network (CON) model which presents a well-defined mathematical structure, facilitating the integration of established control strategies. Key improvements of the CON model over existing latent space control methods include its mathematical structure, stability guarantees, and invertible input-output mapping. This structure allows for better control performance as it enables the use of well-established control techniques like potential-energy shaping. The closed-form approximation of CON dynamics enables efficient training and high-quality control performance. The use of an integral-saturated PID controller with potential force compensation is highlighted as a crucial element, demonstrating successful control of a soft robot using only raw image pixels. This research is a significant step toward developing more efficient and robust latent space control approaches.
CON Network Model#
The Coupled Oscillator Network (CON) model is a novel approach to latent-space control, addressing shortcomings of prior methods. Its core innovation lies in its Lagrangian structure, enabling analytical proof of global Input-to-State stability using Lyapunov arguments. This inherent stability, unlike in previous models, ensures that the learned dynamics preserve the stability properties of the real system. Furthermore, the CON’s architecture facilitates an invertible mapping between input and latent-space forcing, significantly enhancing controllability. This is achieved through an approximated closed-form solution for integration and a trained decoder enabling efficient input reconstruction from latent-space forces. The CON model’s unique combination of stability, invertibility, and mathematical structure allows the application of well-understood control techniques from classical control theory, as demonstrated by achieving high-quality performance in robotic control tasks.
Closed-Form Solution#
The research paper explores the development of an approximate closed-form solution for efficiently integrating complex network dynamics, specifically addressing the computational challenges associated with traditional numerical methods. This is a crucial contribution because numerical integration can be computationally expensive and introduce inaccuracies, especially when dealing with high-dimensional systems or long time horizons. The proposed closed-form solution decomposes the dynamics into simpler, analytically solvable parts (linear, decoupled dynamics) and a residual nonlinear component. This decomposition significantly improves computational efficiency, accelerating training and reducing memory overhead. While the closed-form solution is approximate, the paper demonstrates its accuracy and establishes bounds on the approximation error. The approach’s effectiveness is validated by empirical results showing a substantial speedup in computational time while maintaining acceptable accuracy, highlighting the importance of this efficient solution in practical applications of the developed model.
Soft Robot Control#
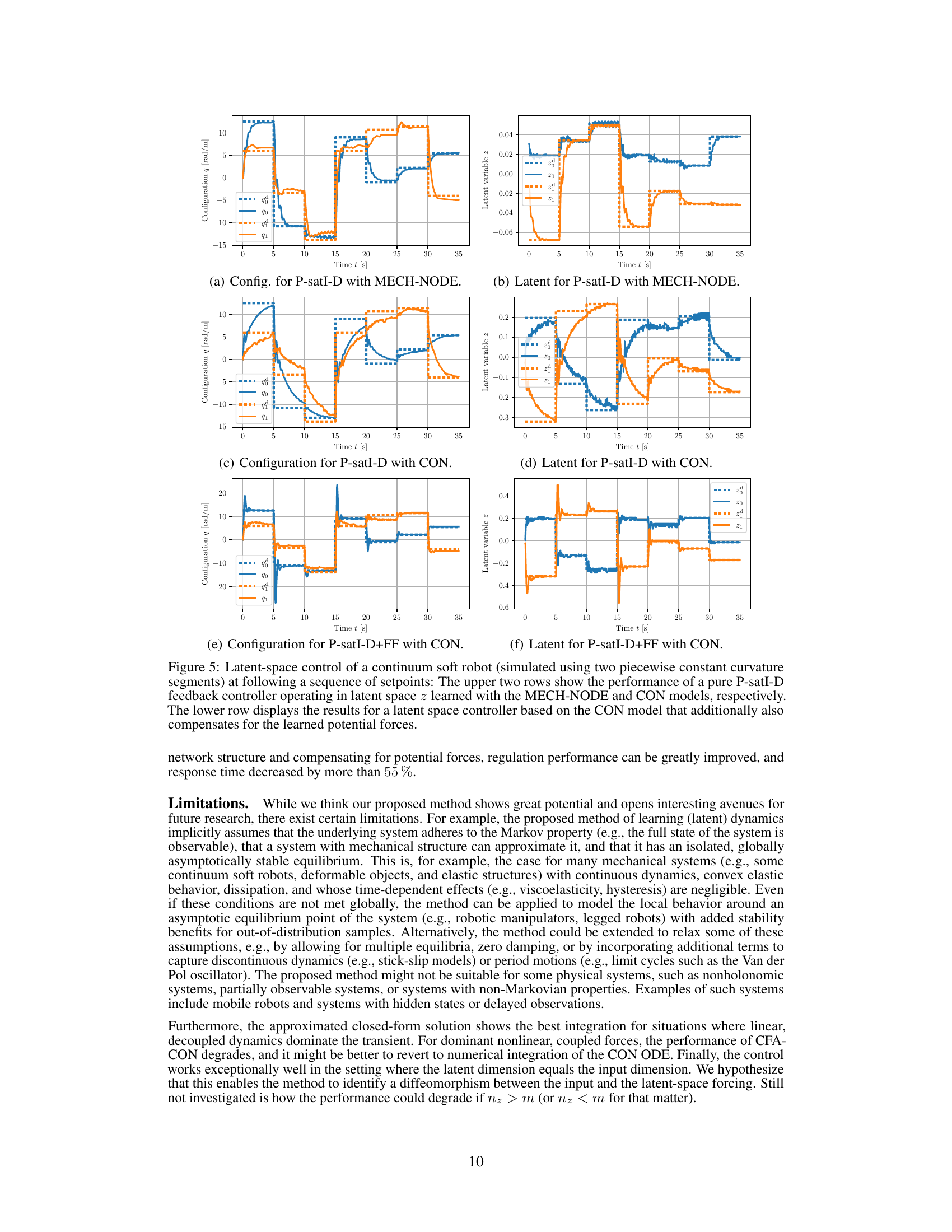
The control of soft robots presents unique challenges due to their inherent flexibility and complex, often nonlinear dynamics. Traditional rigid-body control methods are inadequate, requiring new approaches that leverage the soft robot’s material properties. This research explores model-based control strategies in latent space, directly learning the robot’s dynamics from raw sensory data (images). A novel Coupled Oscillator Network (CON) model is proposed, offering a robust and stable framework for learning and control. Formal proofs of stability are provided, enhancing reliability. The approach addresses the limitations of existing methods by achieving closed-form solutions and employing potential energy shaping, resulting in improved control performance over prior state-of-the-art techniques. The successful application to a soft robot using visual feedback highlights the potential of data-driven, model-based control strategies for advanced soft robotics applications.
Future Work & Limits#
The section on “Future Work & Limits” would ideally delve into several crucial aspects. Firstly, it should address the limitations of the current model, acknowledging its assumptions, such as the Markovian property and reliance on a single, isolated equilibrium. The discussion should explore how these assumptions might be relaxed or adjusted to expand applicability to more complex systems, such as those with nonholonomic constraints, multiple equilibria, or discontinuous dynamics. Secondly, the authors should outline potential future research directions. This could include investigating extensions to handle partially observable systems, incorporating more robust control strategies (beyond PID), or exploring the applicability to different modalities (beyond image data). Addressing the scalability and computational cost of the proposed model for high-dimensional systems is crucial. Finally, a thorough examination of the model’s generalizability across various domains and the potential impact of model misspecification should be presented. Addressing these points would significantly strengthen the paper and provide valuable insights into the model’s potential and limitations.
More visual insights#
More on figures
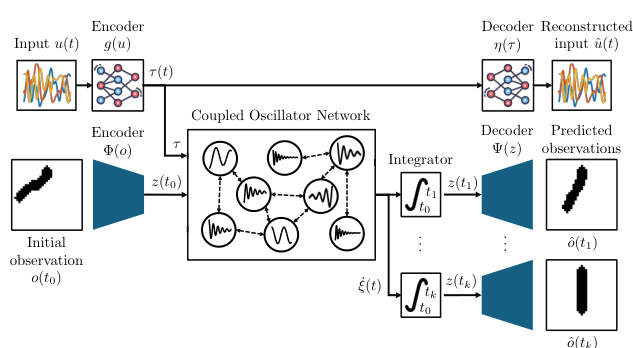
This figure shows the architecture of the proposed Coupled Oscillator Network (CON) for learning latent dynamics from image pixels. Panel (a) illustrates the CON model, which consists of coupled damped harmonic oscillators. The input u(t) is mapped to a forcing term τ(t) through a function g(u). Panel (b) shows how CON is used for learning latent dynamics. The initial observation o(to) and the input u(t) are encoded into the latent space. The CON predicts future latent states, which are then decoded to reconstruct the input û(t) and predict future observations ô(t).
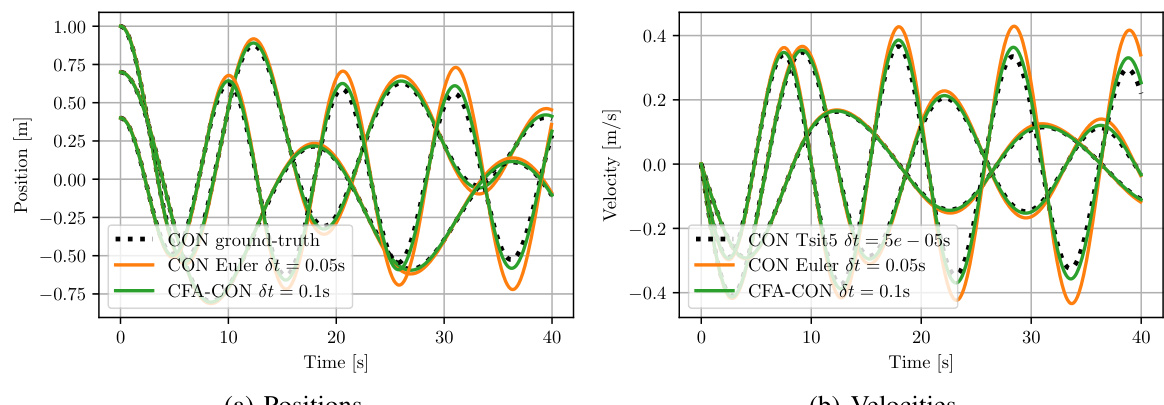
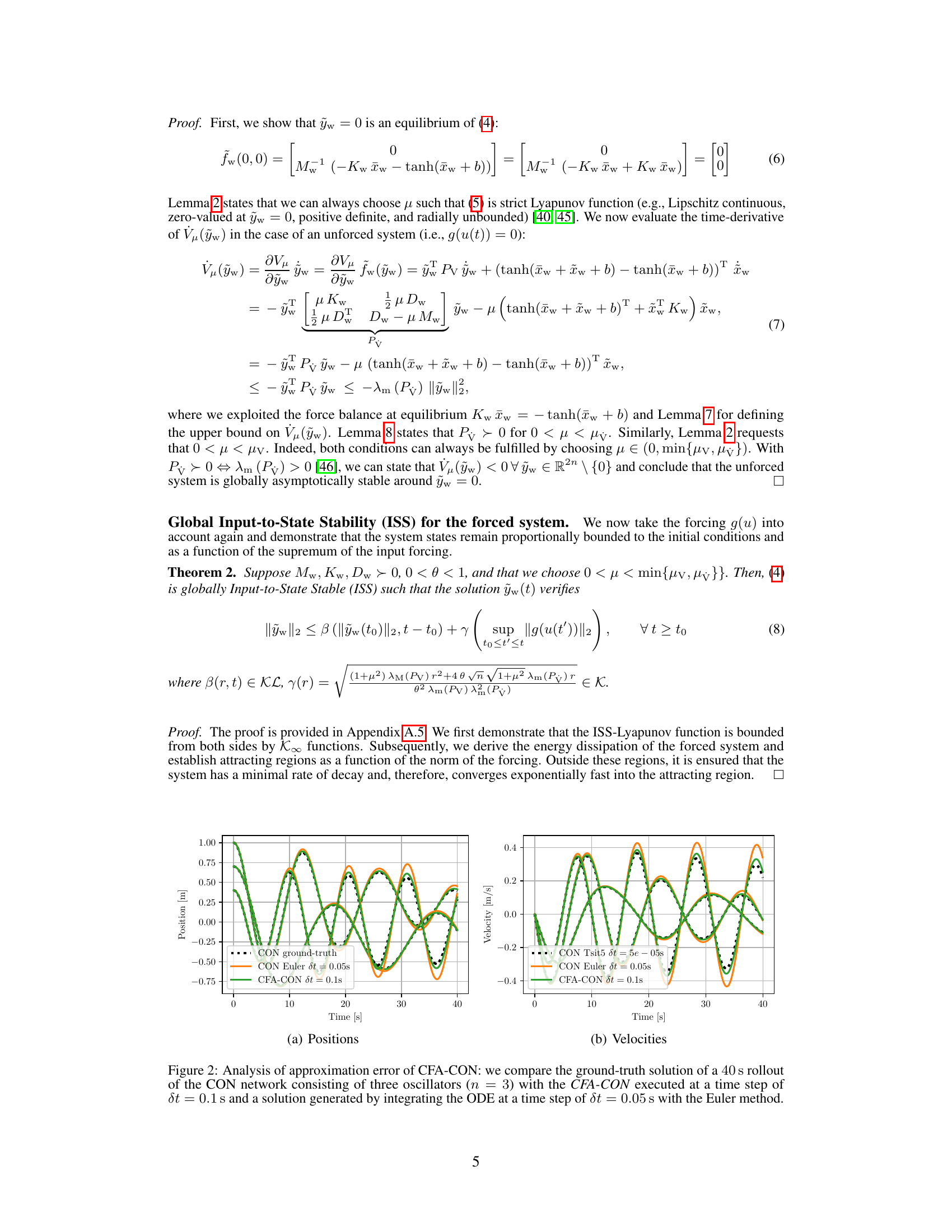
The figure compares the performance of three different methods for integrating the Coupled Oscillator Network (CON) dynamics over 40 seconds. The ground truth is obtained by numerically integrating the CON ODE with a very small time step (5e-5 seconds) using a high-order method. Two approximate methods, the Euler method with a time step of 0.05 seconds, and the Closed-Form Approximation of CON (CFA-CON) with a time step of 0.1 seconds, are compared against the ground truth. The plots show the positions and velocities of the oscillators for each of the three methods.
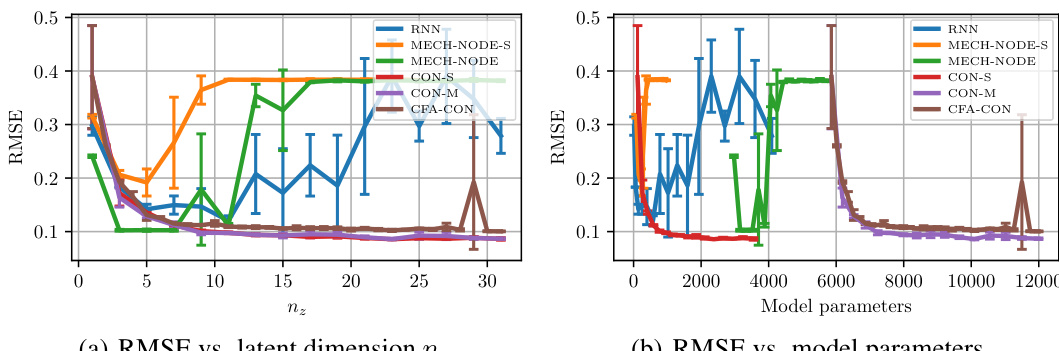
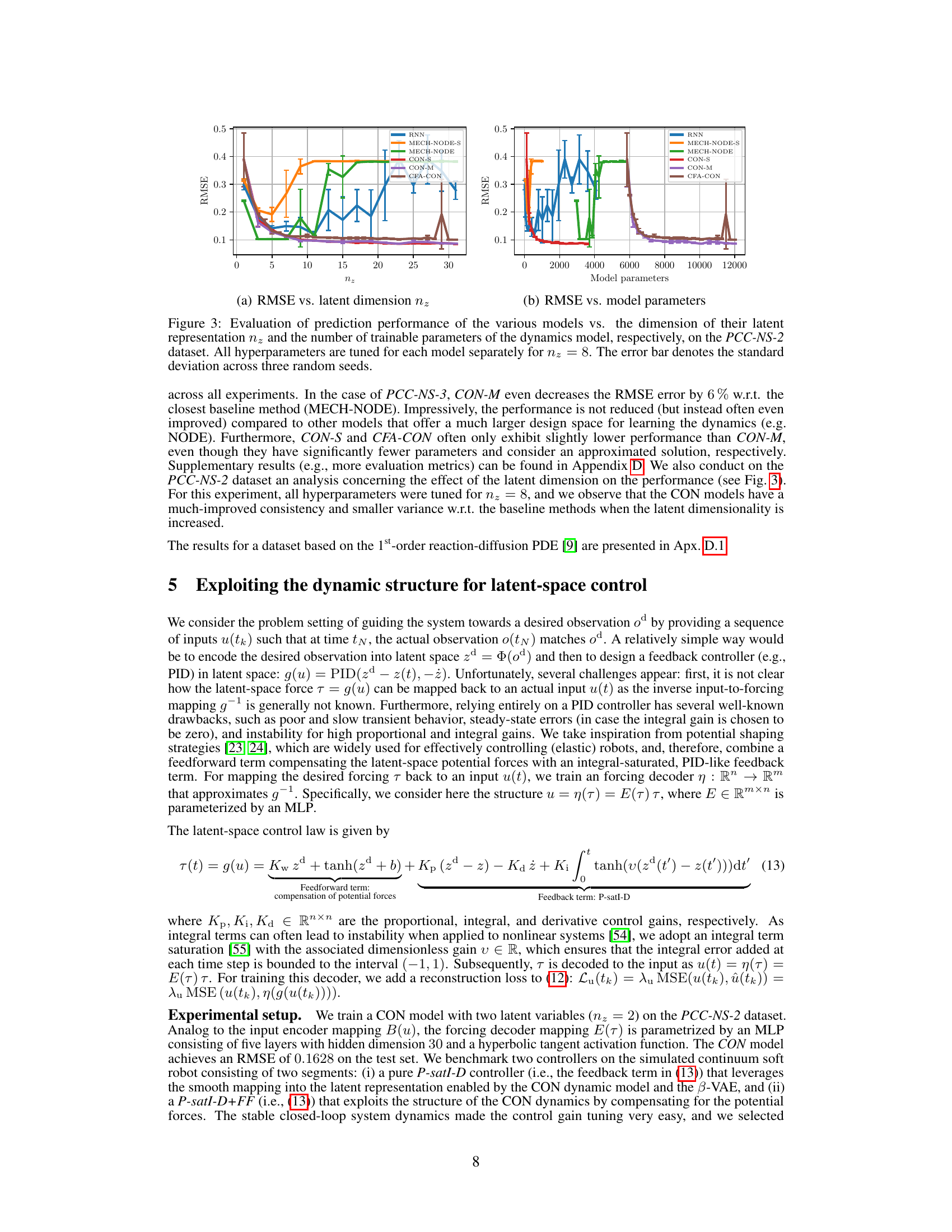
This figure shows the RMSE (Root Mean Squared Error) of different latent dynamic models trained on the PCC-NS-2 dataset (a continuum soft robot with two piecewise constant curvature segments). The left plot compares the RMSE against the latent dimension (nz), while the right plot compares it against the number of trainable parameters. The results show that the CON models (CON-S, CON-M, CFA-CON) achieve better performance and lower variance compared to the other models, especially as the latent dimension increases.
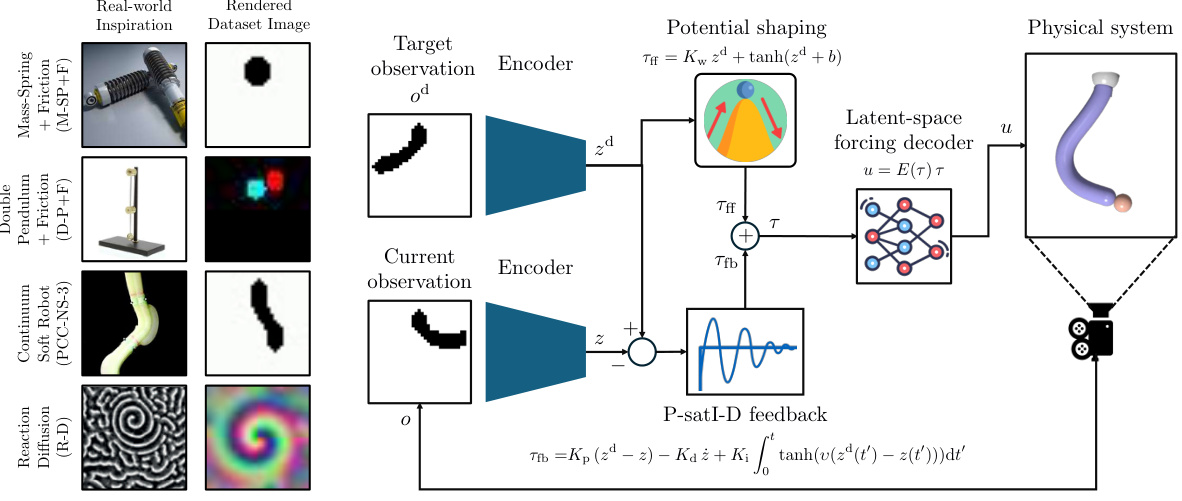
This figure shows the datasets used in the paper and a block diagram of the model-based control system. Panel (a) shows example images from four datasets: Mass-Spring with friction, Single Pendulum with friction, Double Pendulum with friction, and a continuum soft robot. Panel (b) illustrates how the proposed model-based control system works, showing how observations are encoded into a latent space, where a CON model predicts future states, and the control input is calculated based on this prediction and then decoded back into the physical system. It also shows the integral saturated PID with potential force compensation used for control.
The figure compares the performance of three different methods for approximating the dynamics of a coupled oscillator network: the ground truth, the CFA-CON method with a time step of 0.1 seconds, and the Euler method with a time step of 0.05 seconds. The plots show the positions and velocities of the oscillators over time. The CFA-CON method provides a reasonable approximation, especially for the positions, whereas the Euler method shows larger errors, particularly in the velocities.
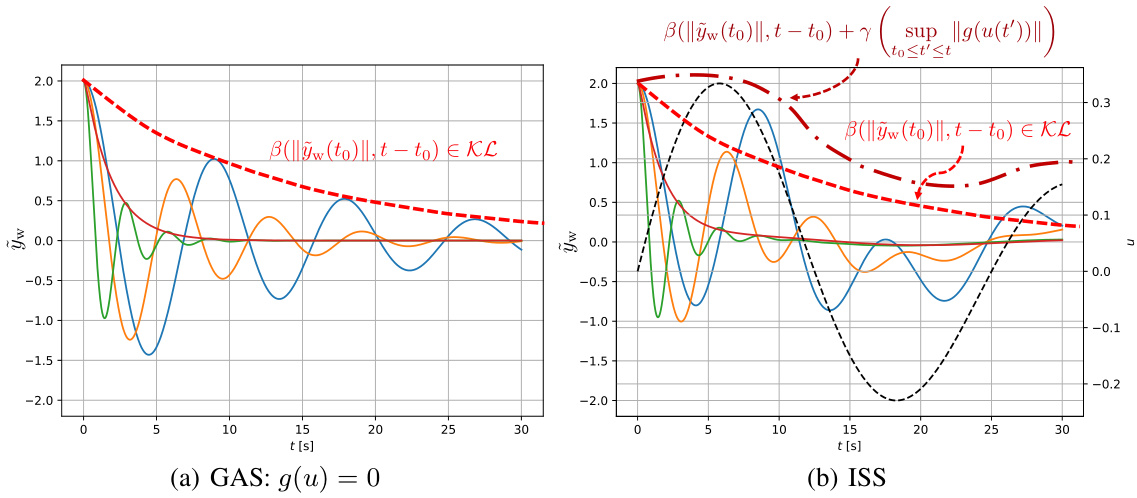
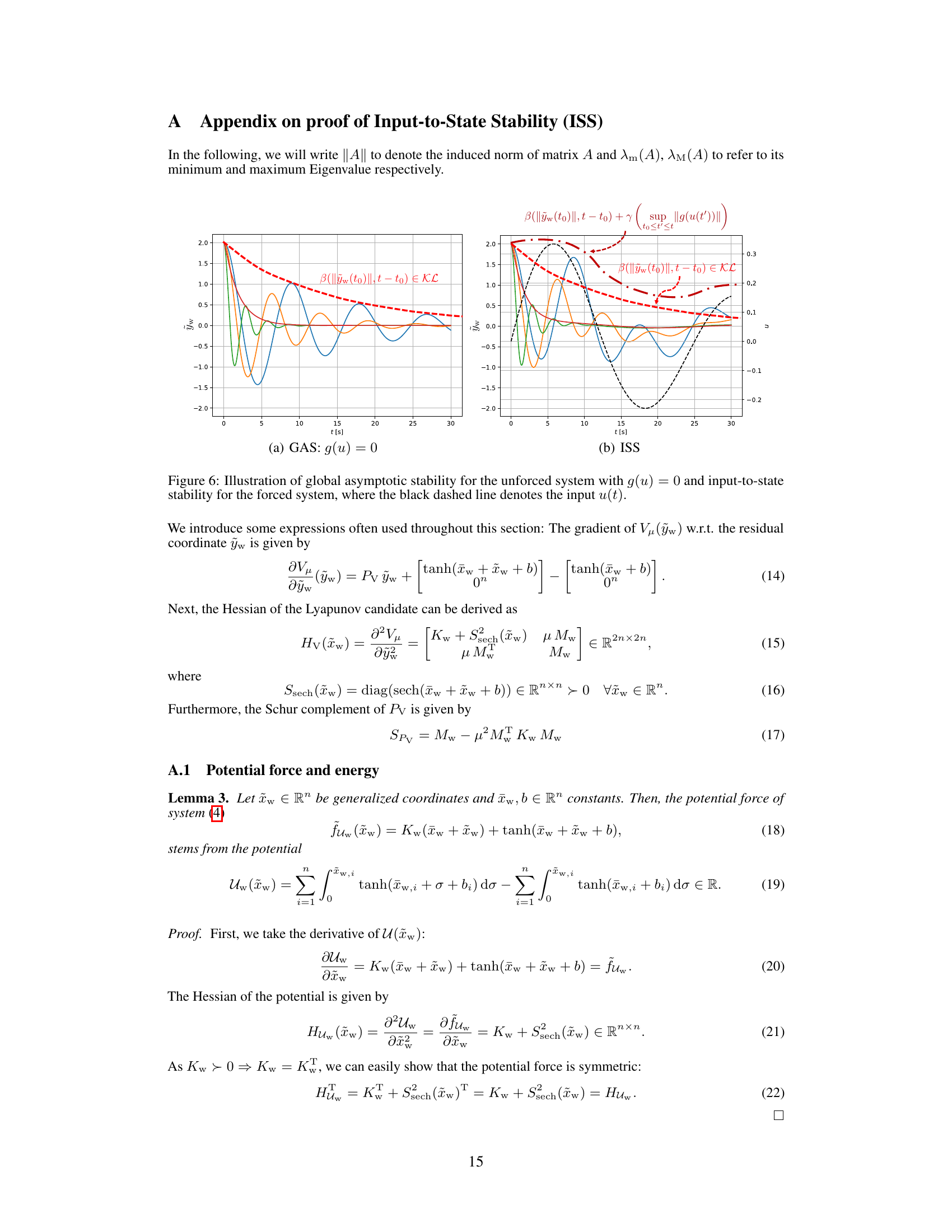
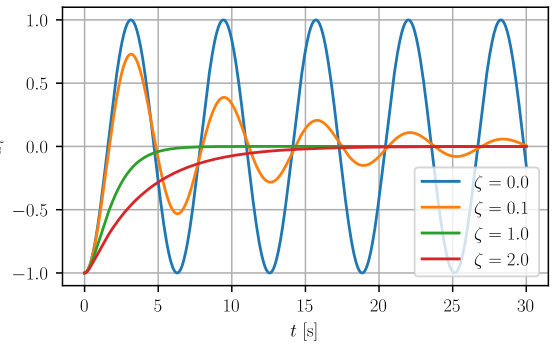
The figure consists of two subfigures: (a) GAS and (b) ISS. Subfigure (a) shows the decay of the residual dynamics for the unforced system (g(u) = 0). It illustrates that the system converges to the equilibrium point asymptotically. Subfigure (b) demonstrates the input-to-state stability (ISS) property for the forced system. Here, the system’s state remains bounded in proportion to the input, as shown by the red dashed line representing the upper bound. The black dashed line represents the input u(t).
The figure shows the architecture of the Coupled Oscillator Network (CON) model and how it’s used for learning latent dynamics from image pixels. Panel (a) details the CON’s structure: a network of coupled damped harmonic oscillators with a nonlinear coupling term and external input. Panel (b) illustrates the CON’s role in a system that learns latent dynamics from images, using an encoder, CON for dynamics prediction, and a decoder to reconstruct inputs and observations from the latent space.
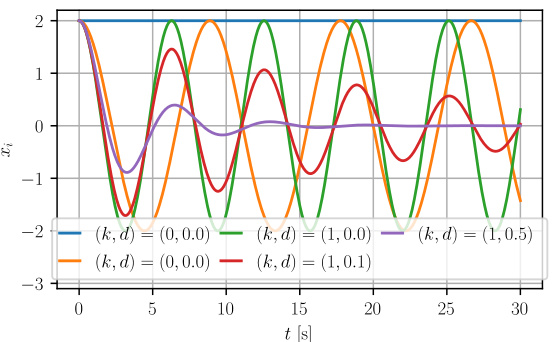
The figure compares the performance of three different methods for integrating the dynamics of a Coupled Oscillator Network (CON). The ground truth is obtained using a high-precision method. One approximation uses a larger time step of 0.1s, and the other uses a smaller time step of 0.05s with the Euler method. The plots show the positions and velocities of the oscillators over time, illustrating the differences in accuracy between the approximation methods and the ground truth. The results demonstrate the trade-off between computational efficiency and accuracy when using different approximation methods.
The figure compares the performance of the proposed closed-form approximation of the Coupled Oscillator Network (CFA-CON) with the ground truth solution obtained by numerically integrating the Ordinary Differential Equation (ODE) using the Euler method. It shows the positions and velocities over a 40-second time period. The CFA-CON is run with a time step of 0.1 seconds, whereas the Euler method uses a smaller time step of 0.05 seconds. The goal is to assess the accuracy of the CFA-CON approximation against the more accurate (but computationally more expensive) numerical integration.
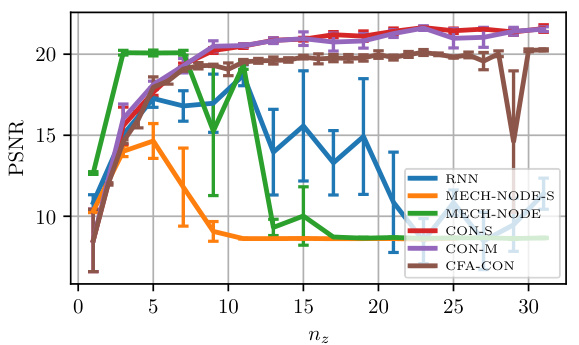
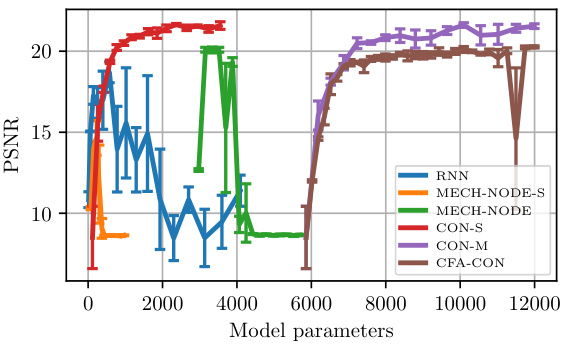
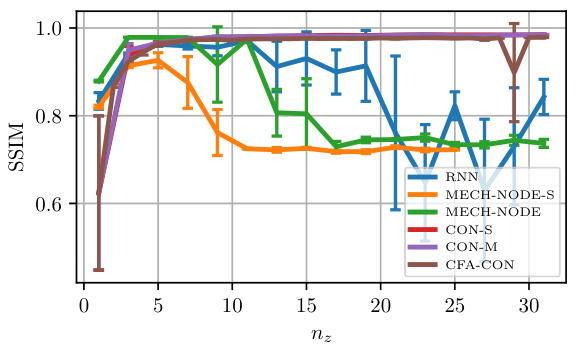
This figure analyzes the performance of various models for predicting future states based on latent representations. It shows how the root mean squared error (RMSE), peak signal-to-noise ratio (PSNR), and structural similarity index (SSIM) change with varying latent dimensions (nz) and model parameters. The hyperparameters were tuned separately for each model and dataset, with a fixed latent dimension of 8 for parameter tuning.
The figure shows the RMSE error for different latent dynamic models trained on the PCC-NS-2 dataset. The left plot shows how the RMSE changes with the latent dimension nz. The right plot shows how the RMSE changes with the number of trainable parameters. The error bars represent the standard deviation across three random seeds.
This figure compares the prediction performance (RMSE) of several models (RNN, GRU, coRNN, NODE, MECH-NODE, CON-S, CON-M, CFA-CON) against the latent dimension (nz) and the number of trainable parameters. The PCC-NS-2 dataset is used for this evaluation. The hyperparameters for all models were tuned for a latent dimension of 8, and the error bars show the standard deviation across three trials with different random seeds.
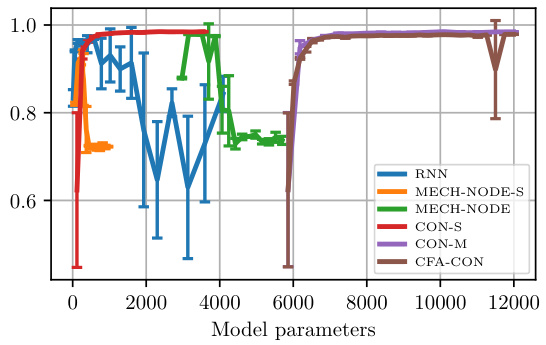
This figure compares the performance of different latent dynamic models in terms of RMSE (Root Mean Squared Error) against the dimension of the latent space (nz) and the number of trainable parameters. The PCC-NS-2 dataset is used, and hyperparameters are tuned for each model separately (nz = 8). Error bars represent the standard deviation across three different random seeds, showcasing the consistency and reliability of the results.
The figure shows the RMSE (Root Mean Square Error) of different models in predicting the dynamics of a continuum soft robot. The x-axis represents the latent dimension (nz) and the number of model parameters. The plot demonstrates the performance of various models (RNN, GRU, coRNN, NODE, MECH-NODE, CON-S, CON-M, CFA-CON) as latent dimension and model parameters increase. The error bars represent the standard deviation from three different trials.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) model. Panel (a) illustrates the CON’s structure: It consists of multiple coupled damped harmonic oscillators. The oscillators’ interactions are governed by a nonlinear coupling function and stiffness and damping terms. The input to the system is mapped to a forcing term that affects the oscillators. Panel (b) illustrates how the CON is used for learning latent dynamics: input and initial observation are encoded into a latent space. The CON predicts the future latent states, which are decoded to produce predicted observations and latent-space torques.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) and how it’s used for learning latent dynamics from image pixels. Panel (a) details the CON’s structure, which consists of interconnected damped harmonic oscillators whose dynamics are influenced by an input and nonlinear coupling. Panel (b) illustrates how the CON is integrated into a larger system for learning latent dynamics. The initial image and input are encoded into a latent space, where the CON predicts future latent states. These states are then decoded to reconstruct future images and control inputs.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) model and how it is used for learning latent dynamics from image pixels. Panel (a) details the CON’s structure, illustrating its composition of coupled damped harmonic oscillators with nonlinear coupling. Panel (b) illustrates the CON’s application in a latent-space learning framework, demonstrating how an encoder maps input and initial observations into a latent space, the CON predicts future latent states, and a decoder reconstructs the input and observations. This process allows for control in the latent space.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) and how it is used for learning latent dynamics from pixel data. Panel (a) details the CON architecture, highlighting its components such as coupled damped harmonic oscillators, the nonlinear coupling term, and the input-to-forcing mapping. Panel (b) illustrates the CON’s application in learning latent dynamics, showing how an encoder maps the initial observation and input into the latent space, and the decoder reconstructs future latent states and torques.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) and how it is used for learning latent dynamics from pixels. Panel (a) details the CON’s structure, illustrating its composition of coupled damped harmonic oscillators and the input-to-forcing mapping. Panel (b) outlines the process of latent-space dynamics learning, involving encoding initial observations and inputs, using the CON for prediction, and decoding the latent-space torques and states.

This figure compares the ground truth positions and velocities of a CON with three oscillators against those obtained using two approximation methods: the CFA-CON method with a larger time step (0.1s) and the Euler method with a smaller time step (0.05s). The comparison highlights the approximation errors introduced by the CFA-CON and Euler methods, demonstrating that CFA-CON’s error is comparable to that of the Euler method, albeit at a larger time step. This suggests that CFA-CON provides a computationally efficient alternative for approximating the CON dynamics.

This figure shows the architecture of the proposed Coupled Oscillator Network (CON) and how it’s used for learning latent dynamics from pixels. Panel (a) details the CON’s structure, illustrating n coupled damped harmonic oscillators whose state is determined by their positions and velocities. Input u(t) is mapped through g(u) to a forcing τ that acts on the oscillators. Panel (b) illustrates how CON learns from pixel data. An encoder maps initial observations o(to) and input u(t) into latent space, where CON predicts future states. A decoder then reconstructs both the latent torques τ(t) and the predicted latent states z(t).
This figure shows the architecture of the proposed Coupled Oscillator Network (CON) model. Panel (a) illustrates the network’s structure: n damped harmonic oscillators coupled through a nonlinear connection and external forcing. Panel (b) demonstrates how CON is used for learning latent dynamics from images. The initial observation and input are encoded into a latent space, CON predicts future latent states, and a decoder reconstructs inputs and observations.
This figure illustrates the architecture of the Coupled Oscillator Network (CON) and how it’s used for learning latent-space dynamics from image pixels. Panel (a) shows the CON’s structure: n coupled damped harmonic oscillators with connections influenced by a hyperbolic tangent function. Panel (b) details the CON’s application in learning dynamics. Initial observations and inputs are encoded into latent space. The CON then predicts future states in this low-dimensional space, before decoding back to the original high-dimensional space (e.g., image pixels).
This figure shows the architecture of the Coupled Oscillator Network (CON) and how it’s used for learning latent dynamics from image pixels. Panel (a) details the CON’s structure: interconnected damped harmonic oscillators influenced by an input and non-linear coupling. Panel (b) illustrates the CON’s application in a control system: image input and previous input are encoded, the CON predicts future latent states, and these are decoded to obtain predicted observations and control signals.
This figure compares three different methods for approximating the CON model’s dynamics: the ground truth solution (high accuracy, high computation cost), CFA-CON (approximation method, medium accuracy and computation cost), and Euler integration (low accuracy and computation cost). The plots show the position and velocity of the oscillators over time. The goal is to show that the CFA-CON method provides a good balance between accuracy and computational efficiency.
The figure compares the performance of three different methods for integrating the CON network dynamics: the ground truth solution (obtained by high-precision numerical integration), the CFA-CON method (an approximate closed-form solution), and the Euler method. The results are shown for both the positions and velocities of the oscillators over a 40-second time period. It demonstrates the accuracy of the CFA-CON approximation compared to the ground truth, highlighting its computational efficiency.
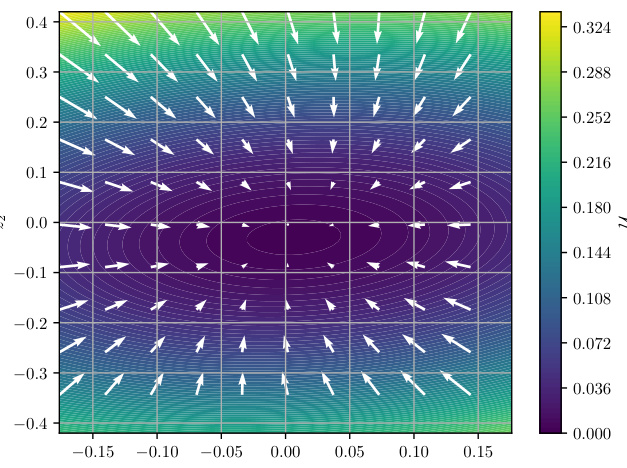
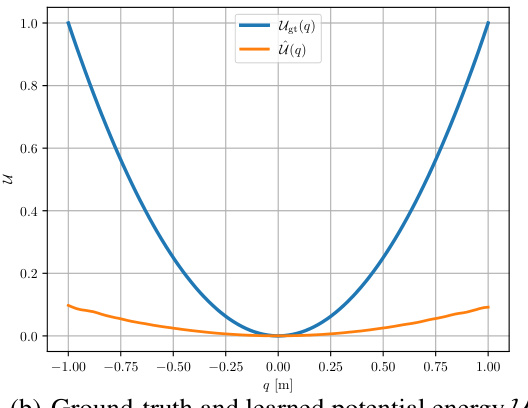
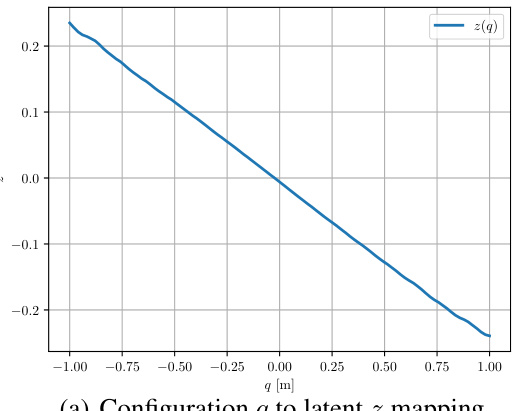
This figure visualizes the potential energy landscapes learned by the CON model for a two-segment continuum soft robot. It shows how the model learns the potential energy as a function of both the latent representation and the robot’s configuration. The visualizations aid in understanding the model’s ability to capture the system’s dynamics.
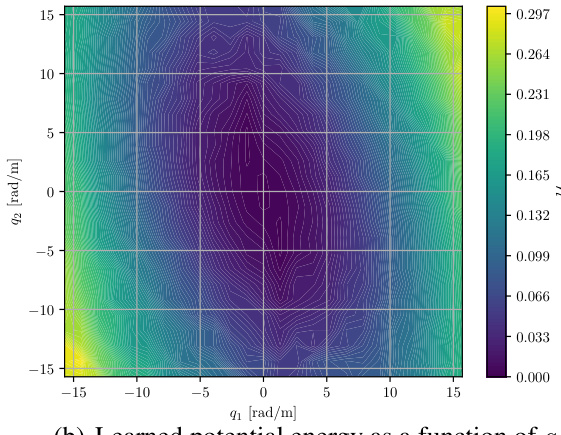
This figure visualizes the potential energy landscapes obtained from a CON model trained on a two-segment continuum soft robot, comparing it to the ground truth. It shows three panels. Panel (a) shows the potential energy as a function of the latent representation. Panel (b) shows the potential energy as a function of the robot’s configuration (which the model doesn’t directly observe). Panel (c) displays the ground truth potential energy for comparison. The color scales represent the potential energy, and the arrows show the direction and magnitude of the potential force.
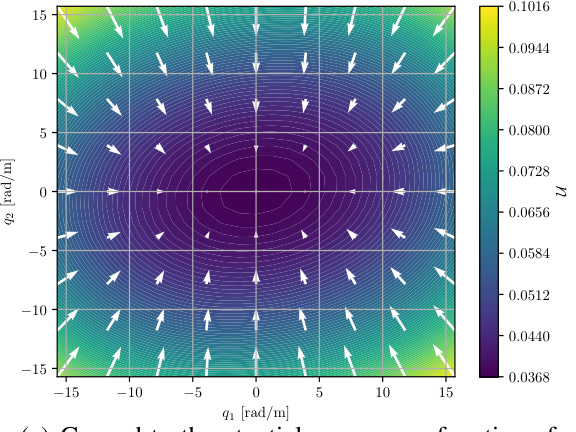
This figure visualizes the potential energy landscape learned by the CON model for a two-segment continuum soft robot. It compares the learned potential energy in latent space and configuration space with the ground truth potential energy. The arrows show the direction and magnitude of the potential forces.

The figure compares the performance of three different methods for integrating the dynamics of a Coupled Oscillator Network (CON). The ground truth is calculated by a high-precision numerical integration method. The second method uses the proposed closed-form approximation (CFA-CON) with a larger time step, and the third method uses a simpler Euler method with a smaller time step. The plots show position and velocity over time, demonstrating that CFA-CON provides a reasonable approximation of the ground truth with significantly improved computational efficiency.
The figure compares the performance of three different methods for approximating the dynamics of a coupled oscillator network. The ground truth is obtained by numerically integrating the network’s ordinary differential equations (ODEs) using a high-precision method (presumably a high-order numerical solver). Two approximation methods are compared against this ground truth: 1) CFA-CON (Closed-Form Approximation of the Coupled Oscillator Network) with a larger time step (dt = 0.1 s) and 2) a lower-order numerical solver (Euler method) with a smaller time step (dt = 0.05s). The plots show the positions and velocities of the oscillators over time for each method, illustrating the approximation error of the two approximate methods.
The figure compares the performance of three different methods for integrating the dynamics of a coupled oscillator network: ground truth, CFA-CON with a time step of 0.1s, and Euler method with a time step of 0.05s. The plot shows the positions and velocities of the oscillators over time, highlighting the approximation error introduced by CFA-CON and the Euler method compared to the ground truth.
The figure compares three methods for approximating the CON’s dynamics: the ground truth solution (obtained via high-accuracy numerical integration), CFA-CON (the proposed closed-form approximation), and Euler integration. It shows the position and velocity outputs over time and highlights the accuracy of CFA-CON in comparison to the other methods.
More on tables

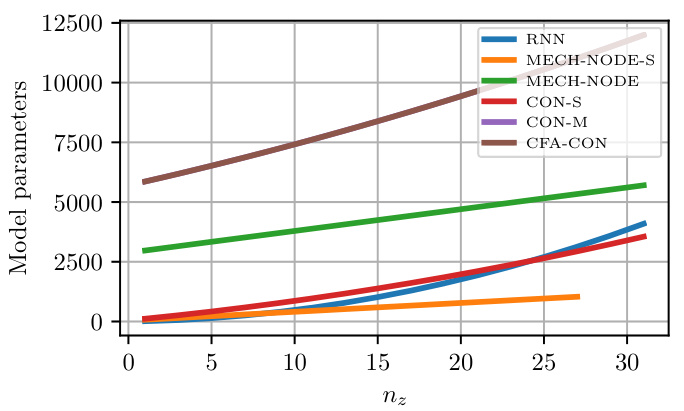
The table presents the number of trainable parameters for several latent dynamic models. It compares the parameter counts across different models (RNN, GRU, coRNN, NODE, MECH-NODE, CON-S, CON-M, CFA-CON) for three different datasets representing the complexity of the underlying dynamics. The datasets are: Mass-spring with friction (M-SP+F), Double pendulum with friction (D-P+F), and a continuum soft robot with two piecewise constant curvature segments (PCC-NS-2). The number of latent dimensions (nz) is also specified for each dataset.
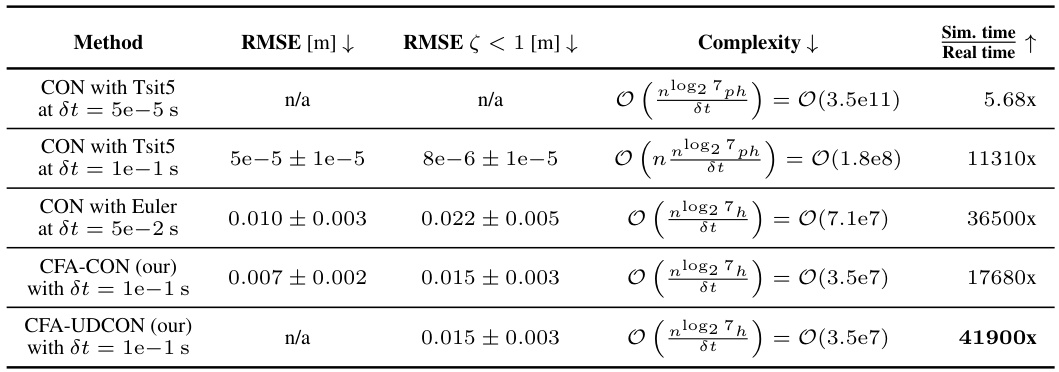
The table compares different methods for integrating the CON dynamics. It shows the root mean square error (RMSE) of each method compared to a high-accuracy baseline (Tsit5), the computational complexity, and the simulation time relative to real time. The methods compared include using Tsit5 and Euler methods at different time steps, as well as the proposed CFA-CON and CFA-UDCON methods. The RMSE is given for all data and for data containing only underdamped oscillators.
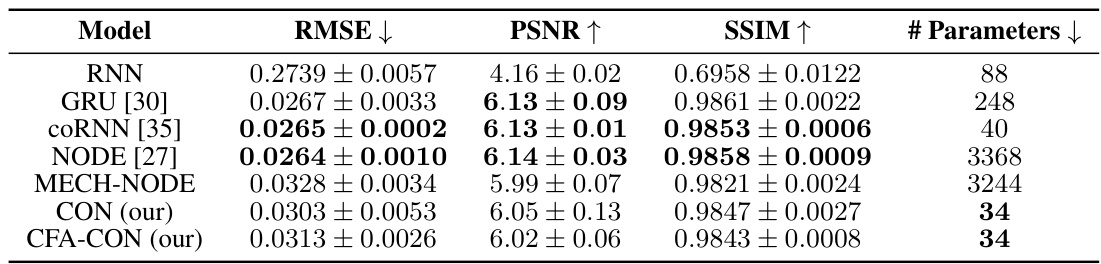
The table compares the performance of the proposed CON and CFA-CON models against several baseline methods on six different datasets. Three datasets involve simple mechanical systems (mass-spring, single pendulum, double pendulum), and three datasets involve a continuum soft robot with varying complexity (one segment, two segments, three segments). The table shows the RMSE (root mean square error), PCC (Pearson correlation coefficient), and the number of parameters for each model. The results are averaged over three different random seeds to demonstrate statistical significance.
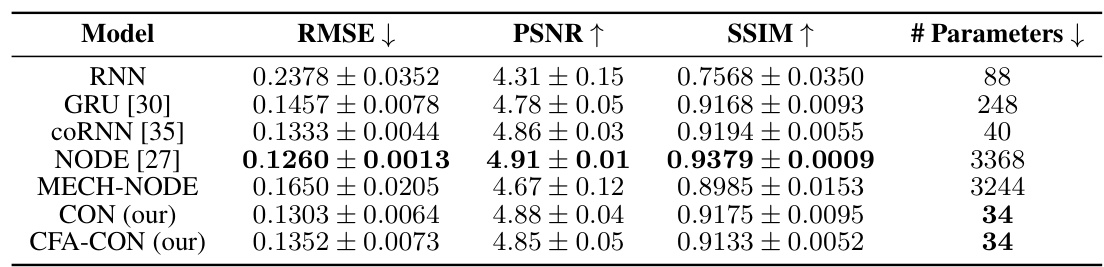
This table benchmarks the performance of the proposed CON and CFA-CON models against several other popular latent space model architectures for learning latent dynamics. It uses six datasets: three unactuated mechanical systems (mass-spring, single pendulum, and double pendulum) and three actuated continuum soft robots with varying complexity. The results show the RMSE, PCC (Pearson correlation coefficient), and the number of parameters for each model on each dataset, demonstrating the accuracy and efficiency of CON and CFA-CON compared to the baselines.
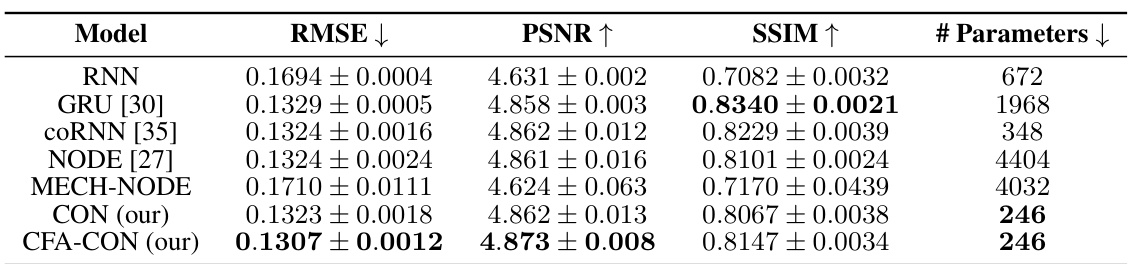
This table compares the performance of the proposed CON and CFA-CON models against various baseline methods (RNN, GRU, coRNN, NODE, MECH-NODE) on six different datasets. Three datasets involve simple unactuated mechanical systems (mass-spring, single pendulum, double pendulum), while the remaining three datasets involve a continuum soft robot with varying complexity (one segment with constant planar strains, two segments with piecewise constant curvature, three segments with piecewise constant curvature). The table reports the root mean squared error (RMSE) for each model on each dataset, along with the Pearson correlation coefficient (PCC) for the PCC-NS-2 and PCC-NS-3 datasets. Different latent dimensions (nz) are used for different datasets to optimize performance. The results are averaged over three different random seeds to account for variability.
This table benchmarks the performance of the proposed Coupled Oscillator Network (CON) and its closed-form approximation (CFA-CON) against other state-of-the-art methods for learning latent dynamics. It uses six datasets: three unactuated mechanical systems (mass-spring, single pendulum, double pendulum) and three actuated continuum soft robot systems with varying complexity (one, two, and three segments). The table shows RMSE, PCC (Pearson correlation coefficient), and the number of parameters for each model, highlighting the CON’s efficiency and competitive performance.
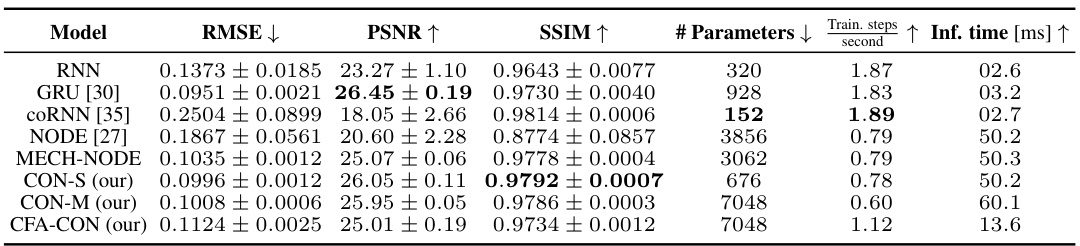
This table compares the performance of the proposed Coupled Oscillator Network (CON) and its closed-form approximation (CFA-CON) against other state-of-the-art methods for learning latent dynamics on six different datasets. The datasets include both unactuated simple mechanical systems (mass-spring, pendulum) and actuated continuum soft robots with varying complexity. The table shows the RMSE (root mean square error) for each model and dataset, providing a quantitative comparison of their prediction accuracy.
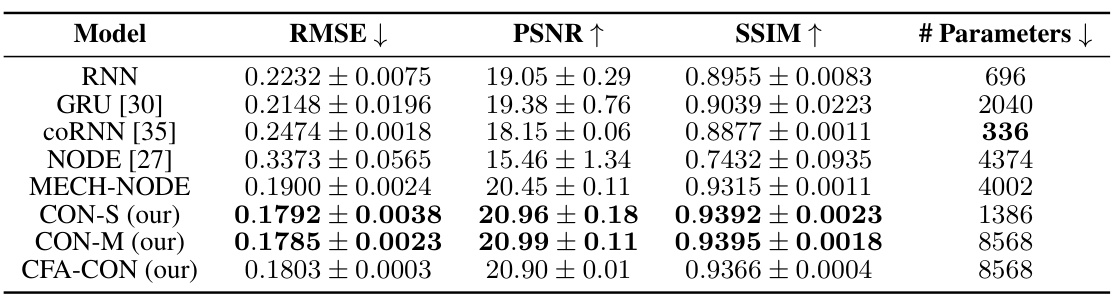
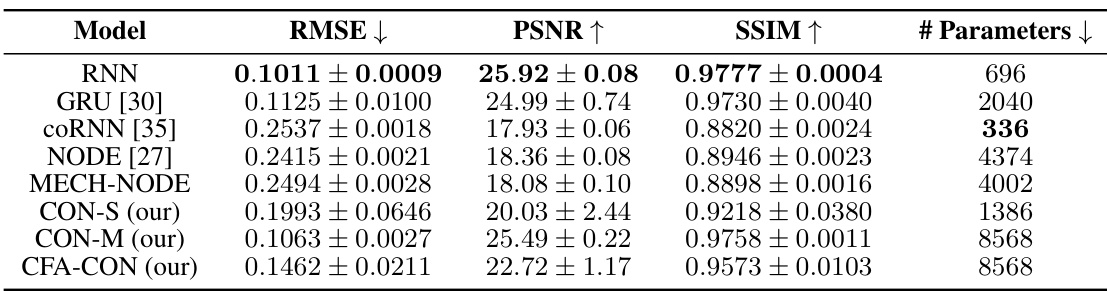
This table compares the performance of different models in learning latent dynamics, specifically focusing on a soft robot with three segments. It shows RMSE, PSNR, SSIM, and the number of parameters for each model. The CON models (CON-S and CON-M) demonstrate competitive performance compared to other models, including a NODE model with prior knowledge about the mechanical structure.
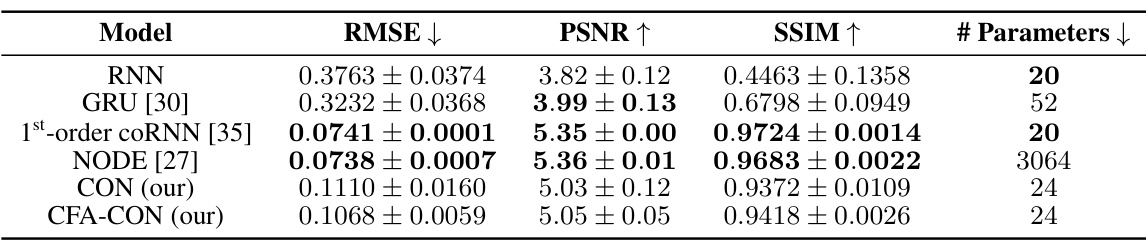
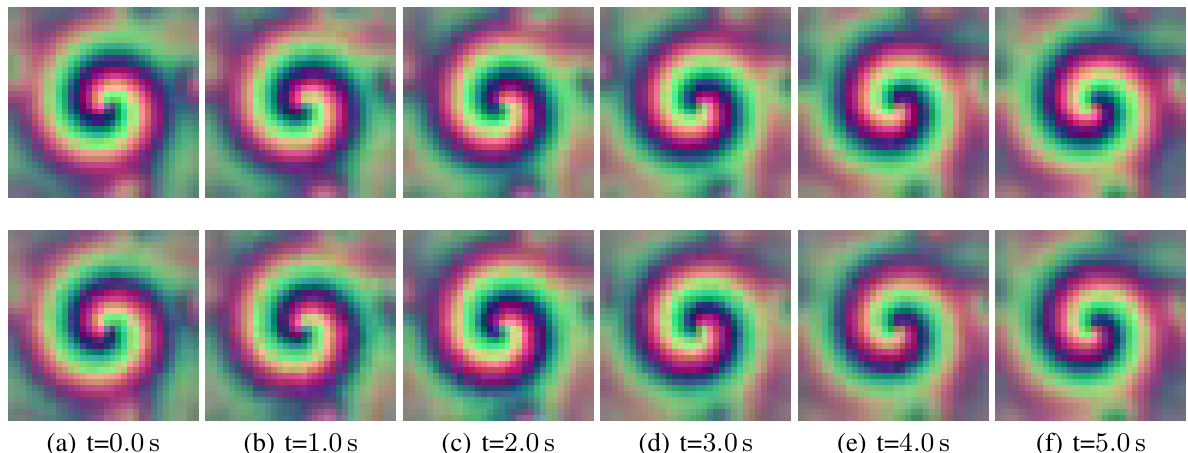
This table compares the performance of different latent dynamic models on the Reaction-Diffusion dataset. It highlights the RMSE, PSNR, and SSIM metrics, along with the number of parameters for each model. Notably, it uses 1st-order versions of the models due to the dataset’s 1st-order PDE dynamics and excludes input mapping parameters because the dataset lacks system inputs.
Full paper#