↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Solving complex Partial Differential Equations (PDEs) efficiently and accurately is a major challenge. Traditional mesh movement methods are computationally expensive and struggle with complex geometries. Learning-based approaches lack generalization, requiring retraining for each new PDE or geometry. They often suffer from robustness issues, such as inverted elements.
This research introduces Universal Mesh Movement Network (UM2N). UM2N uses a Graph Transformer encoder and Graph Attention Network decoder. Trained on a PDE-independent dataset, UM2N generalizes to unseen PDEs and geometries without retraining. Evaluation shows UM2N outperforms existing methods in accuracy and speed, even handling cases where traditional methods fail. The method also exhibits enhanced robustness to mesh tangling.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computational fluid dynamics and numerical methods due to its introduction of a novel, universal mesh movement network (UM2N). UM2N addresses limitations of existing methods by enabling zero-shot adaptation to various PDEs and geometries, significantly accelerating simulations while improving accuracy. It opens avenues for research into efficient, generalizable mesh adaptation techniques across diverse applications, potentially enhancing simulations of complex physical phenomena and pushing the boundaries of current simulation capabilities.
Visual Insights#

This figure shows a schematic of the Universal Mesh Movement Network (UM2N) architecture. The input consists of an original mesh, its vertices, edges, and a monitor function representing the desired mesh density. The vertices and monitor values, along with positional encoding, are fed into a graph transformer encoder which extracts embeddings. These embeddings, concatenated with edge features, are then processed by a graph attention network (GAT) decoder, which outputs the adapted mesh. The decoder uses multiple GAT blocks to refine the mesh movement iteratively.

This table presents a quantitative comparison of three different mesh movement methods: Monge-Ampere (MA), M2N, and the proposed UM2N. The comparison is done across three different scenarios: Swirl, Cylinder, and Helmholtz. For each scenario and method, the table shows the PDE error reduction ratio (ER) and the computation time in milliseconds. ‘Fail’ indicates cases where mesh tangling occurred, preventing successful simulation.
In-depth insights#
Universal Mesh Movement#
The concept of “Universal Mesh Movement” in the context of numerical PDE solving is intriguing. It suggests a single, trained model capable of adapting meshes across diverse PDE types and complex geometries, eliminating the need for extensive retraining with each new problem. This universality is achieved through sophisticated neural network architectures (like Graph Transformers and Graph Attention Networks) that learn underlying patterns in mesh movement rather than being explicitly trained on specific PDE solutions. The implications are significant: faster and more efficient mesh adaptation, reduced computational costs, and improved accessibility for researchers lacking substantial computational resources. However, the true universality remains a key challenge. While the method demonstrates impressive zero-shot performance in several experiments, limitations exist regarding mesh tangling and reliance on suitable monitor functions. Future work will likely involve further enhancements in robustness and generalization, potentially through more sophisticated loss functions or incorporating other mesh adaptation techniques.
Graph Neural Approach#
A graph neural approach leverages the power of graph theory and neural networks to model complex relationships within data. Its strength lies in handling non-Euclidean data, such as social networks, molecular structures, or citation networks, where traditional machine learning methods struggle. By representing data as graphs with nodes and edges, the approach captures inherent relational information. Neural networks then learn node embeddings or graph representations, enabling tasks like node classification, link prediction, or graph classification. The choice of graph neural network architecture (e.g., Graph Convolutional Networks, Graph Attention Networks) impacts performance and efficiency, depending on the specific application and data characteristics. Key advantages include scalability, interpretability (to an extent), and the ability to incorporate various types of node and edge features. However, challenges remain in handling large graphs efficiently, addressing over-smoothing issues in deeper networks, and ensuring generalization to unseen graph structures. Future developments are likely to focus on improved scalability and efficiency, enhanced explainability, and development of robust training methods.
PDE-Independent Training#
The concept of “PDE-Independent Training” in the context of mesh movement networks represents a significant advancement. Traditional methods often require retraining for each new partial differential equation (PDE), hindering efficiency and scalability. PDE-independent training aims to overcome this limitation by learning a universal mesh movement strategy applicable across various PDEs. This is achieved by decoupling the mesh movement process from the specific PDE being solved. Instead of training on PDE solutions directly, the model learns to move meshes based on features extracted from a monitor function, a measure that indicates desired mesh density. This function, which may reflect solution characteristics like curvature or gradients, provides supervision signals without explicit knowledge of the underlying PDE. This approach significantly enhances the generalization ability of the mesh movement network, making it applicable to different PDE types and boundary conditions without requiring extensive retraining. The key is generating a diverse dataset of monitor functions that effectively capture the diverse characteristics of various PDE solutions. The success of this technique hinges on the ability of the model to effectively learn and generalize from these data-driven features, and thus to disentangle features that are generally useful across multiple equations.
Zero-Shot Generalization#
Zero-shot generalization, in the context of mesh movement networks for solving partial differential equations, is a significant advancement. It implies that a model, trained on a diverse set of mesh configurations and PDE types, can directly and accurately adapt to completely unseen mesh structures and PDEs without any further training or fine-tuning. This capability is highly desirable as it significantly reduces the computational burden and expertise required for solving PDEs in various domains. The key to achieving zero-shot generalization lies in the model’s ability to learn underlying, transferable features and relationships rather than memorizing specific examples. This likely involves architectures designed to handle variations in mesh topology and size distribution, as well as PDE-invariant loss functions that focus on the fundamental principles of mesh adaptation. The success of such a method would mean a more robust and generalizable approach to numerical simulation, transcending the limitations of previous methods requiring extensive retraining for each new problem. However, challenges remain in designing architectures and training procedures that effectively capture the underlying physics of PDEs while maintaining generalization ability. It also raises questions regarding the boundaries of the applicability and potential limitations of this zero-shot approach in handling extremely complex or highly irregular meshes and PDEs, which merit further investigation.
Mesh Tangling Mitigation#
Mesh tangling, a significant challenge in mesh-based numerical simulations, arises when mesh elements overlap or invert, compromising solution accuracy and potentially causing solver crashes. Mitigation strategies are crucial for robust and reliable simulations, particularly in complex scenarios with dynamic boundaries or large deformations. The paper likely explores various approaches, possibly including the use of loss functions that penalize inverted elements during the training of a mesh movement network. This could involve incorporating element volume constraints or employing techniques like optimal transport to guide mesh adaptation. Another potential avenue is the use of sophisticated regularization methods integrated within the mesh movement algorithm to prevent element inversion. The effectiveness of these methods depends on factors like mesh density, boundary conditions, and the specific numerical solver used. A robust mesh tangling mitigation strategy is essential for ensuring the wider applicability and reliability of mesh-based simulations.
More visual insights#
More on figures
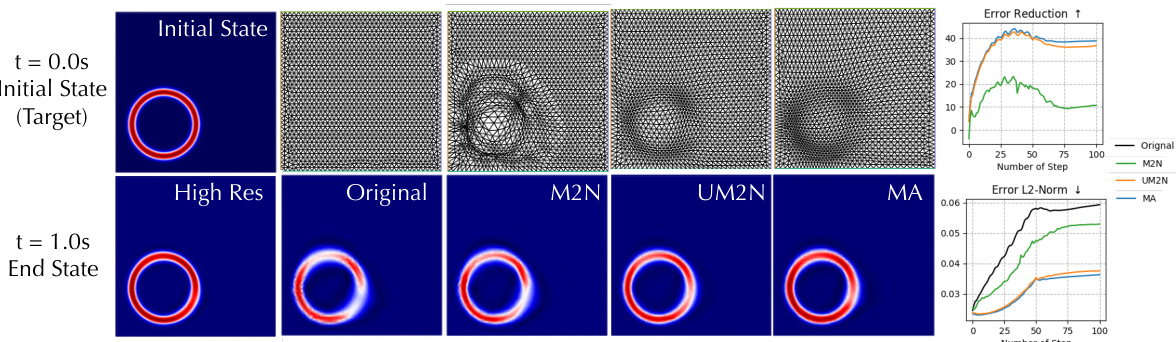
This figure presents a comparison of the results for a swirl case simulation using different methods: UM2N, M2N, and Monge-Ampere (MA). The top row shows the mesh at the end of the simulation and the bottom row shows the solution. The rightmost plot provides quantitative results comparing error accumulation over time steps for each method, highlighting the superior performance of UM2N and MA in suppressing error compared to M2N.
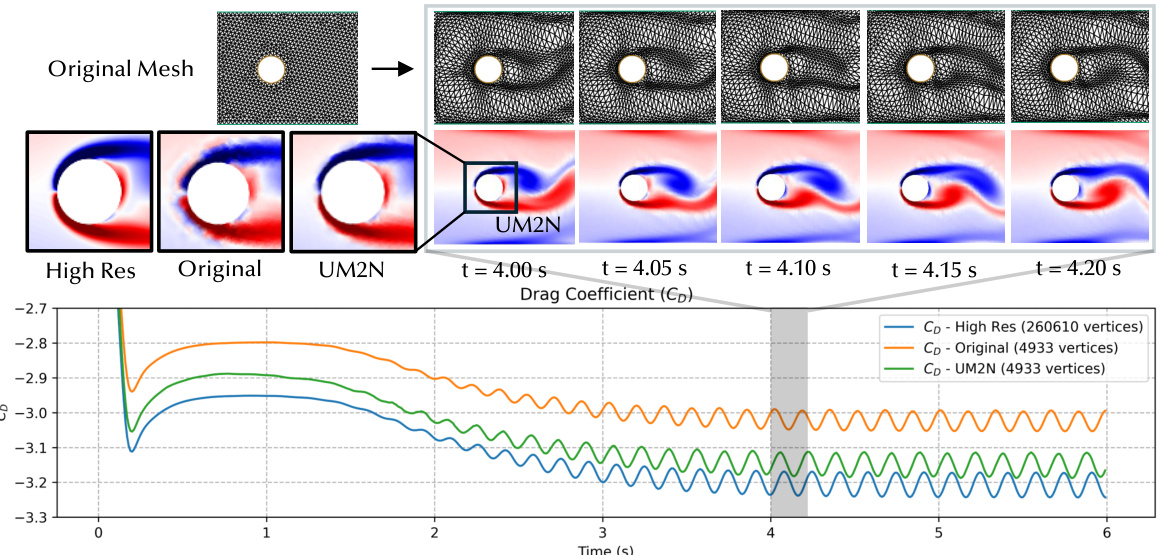
This figure shows the results of a flow past a cylinder simulation using the UM2N method. The top part displays snapshots of adapted meshes and vorticity intensity over time, showcasing the mesh’s ability to adapt to the complex fluid dynamics. The bottom part compares the drag coefficient (CD) obtained using high-resolution, original, and UM2N adapted meshes, demonstrating the improved accuracy and periodicity achieved by UM2N.

This figure analyzes the wake flow vorticity for the flow past cylinder simulation. It shows the adapted mesh generated by UM2N, vorticity error maps for both the original mesh and the UM2N mesh, and quantitative comparisons of vorticity at four cross-sections. The results demonstrate UM2N’s ability to reduce the vorticity difference compared to a high-resolution mesh, improving the accuracy of the simulation.
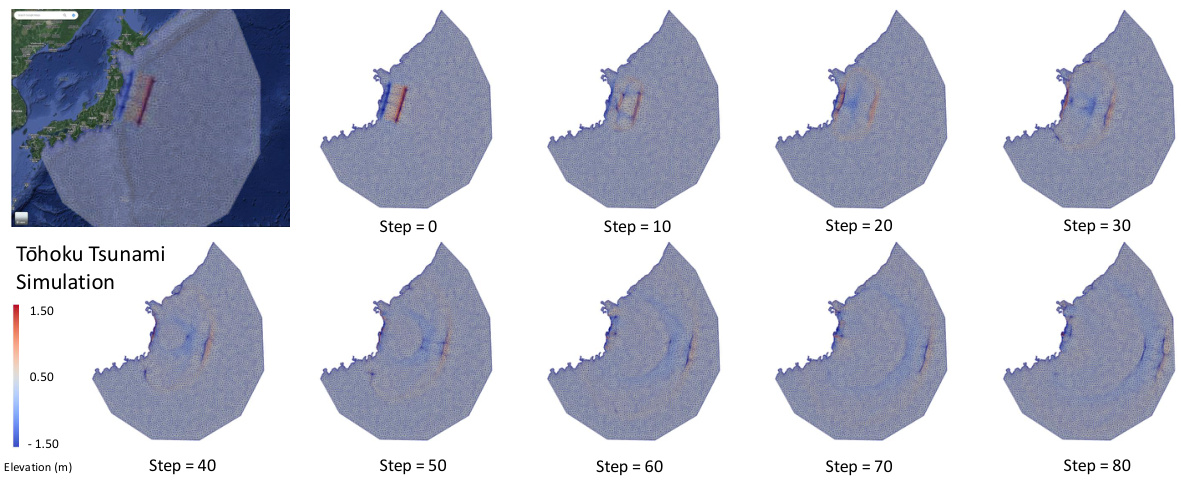
This figure shows the qualitative results of applying the UM2N model to a real-world Tohoku tsunami simulation. The model effectively tracks the wave propagation by dynamically adjusting the mesh resolution, particularly at the wave front where high resolution is needed for accurate simulation. The figure demonstrates the model’s ability to handle complex boundaries and real-world scenarios.
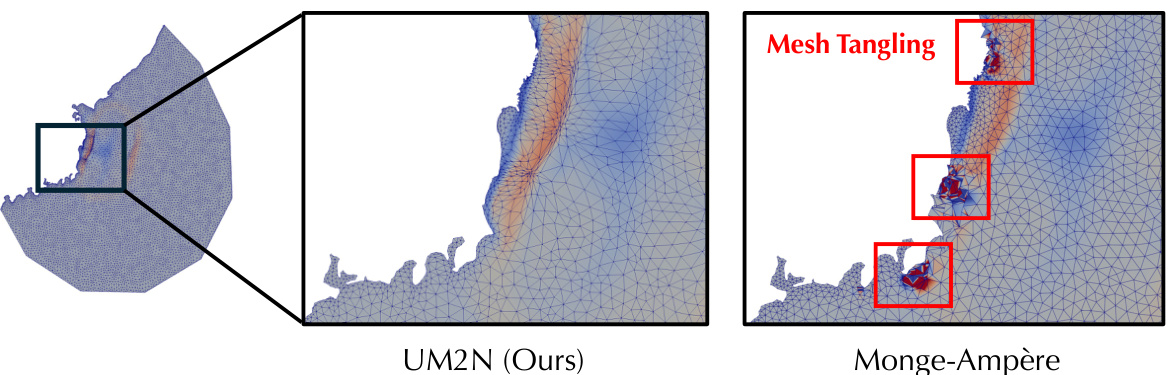
This figure compares the mesh generated by the proposed UM2N method and the Monge-Ampère method near a complex coastline. The Monge-Ampère method produces inverted elements (mesh tangling) in areas highlighted by red boxes. The UM2N, on the other hand, produces a smooth, untangled mesh, demonstrating its robustness in handling complex boundary conditions.
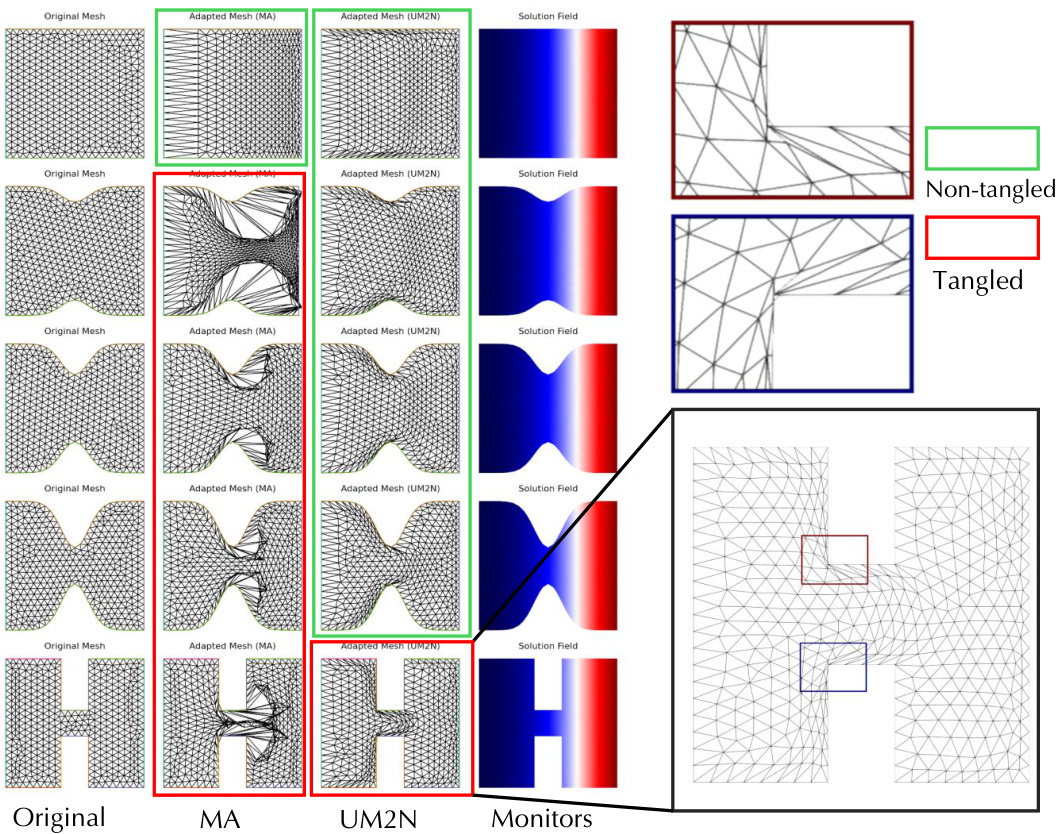
This figure demonstrates a comparison of mesh adaptation results between the proposed Universal Mesh Movement Network (UM2N) and the Monge-Ampere (MA) method on increasingly challenging, non-convex geometries. Each row shows the original mesh, the mesh generated by the MA method, and the mesh generated by UM2N, along with the corresponding solution field. The results highlight the robustness of UM2N against mesh tangling (inverted elements) as the geometry complexity increases from top to bottom. While the MA method fails to produce valid meshes in the more complex cases (bottom rows), UM2N successfully generates non-tangled meshes. This demonstrates UM2N’s enhanced robustness in handling challenging mesh movement tasks.
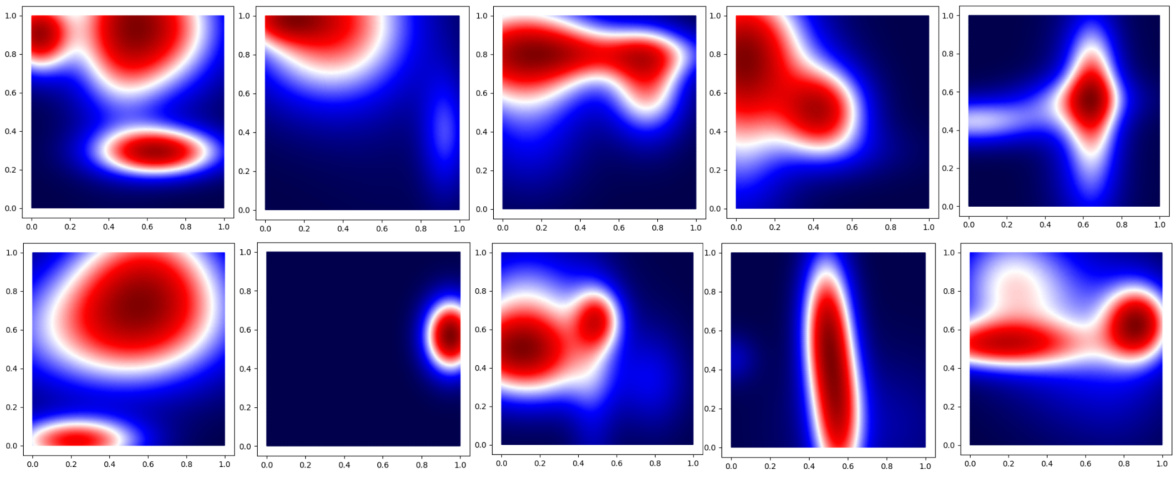
This figure shows ten example images of generated generic fields. These fields are created by summing multiple 2D Gaussian distributions with random parameters (mean, standard deviation, and orientation) to simulate a variety of solution fields, independent of any particular PDE. These fields are used to generate a PDE-independent training dataset for the Universal Mesh Movement Network (UM2N). The variation in these fields demonstrates the diversity that the training data can capture.

This figure compares the results of high-resolution simulation, UM2N, and M2N methods on a flow-past-a-cylinder case. It shows that both UM2N and M2N produce non-tangled meshes in a simplified setting with a lower Reynolds number and slip boundary conditions. UM2N better captures the dynamics and adapts to the PDE solution compared to M2N and High Resolution simulation.
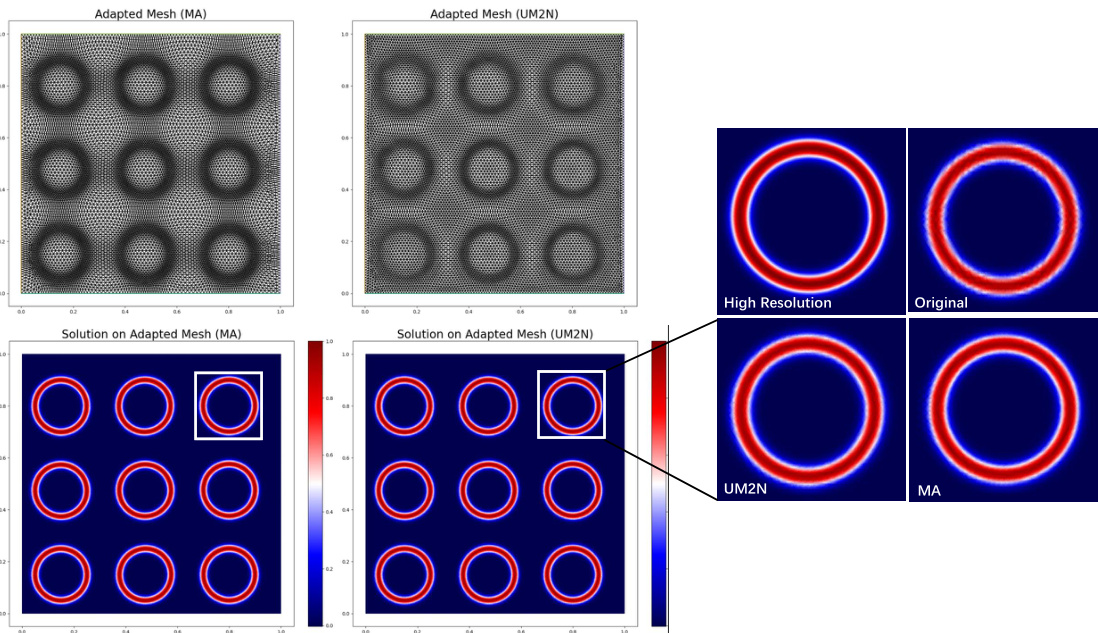
This figure compares the results of mesh adaptation using the Monge-Ampere method (MA) and the proposed Universal Mesh Movement Network (UM2N). The left side shows the adapted meshes generated by each method for a scenario with multiple cylindrical obstacles, alongside the high-resolution reference mesh. The right side presents a comparison of the solutions obtained on these meshes, highlighting the improved accuracy of UM2N compared to MA and the high-resolution reference.
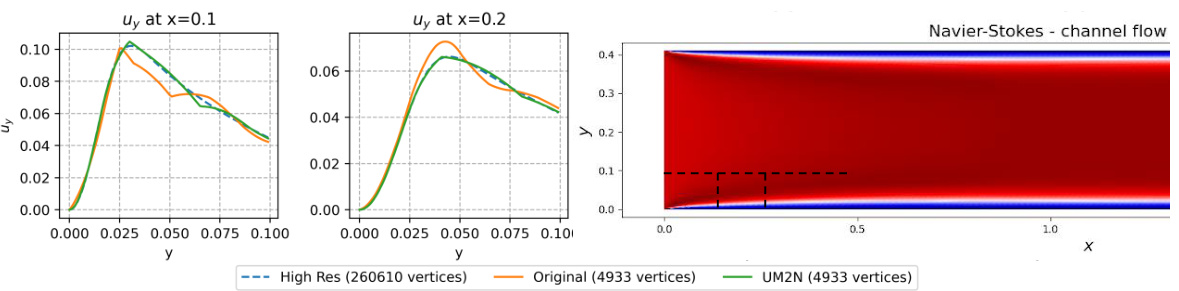
This figure compares the accuracy of velocity (uy) calculation at different y positions (0.1 and 0.2) using three different mesh approaches: high-resolution mesh, original mesh, and UM2N mesh. The results show that the UM2N mesh produces significantly more accurate velocity values, much closer to those obtained with the high-resolution mesh, than the original mesh. The improvement highlights the effectiveness of UM2N in refining mesh resolution where it matters most, leading to better accuracy in the solution. The figure also provides a visual representation of the Navier-Stokes channel flow to contextulize this boundary layer analysis.
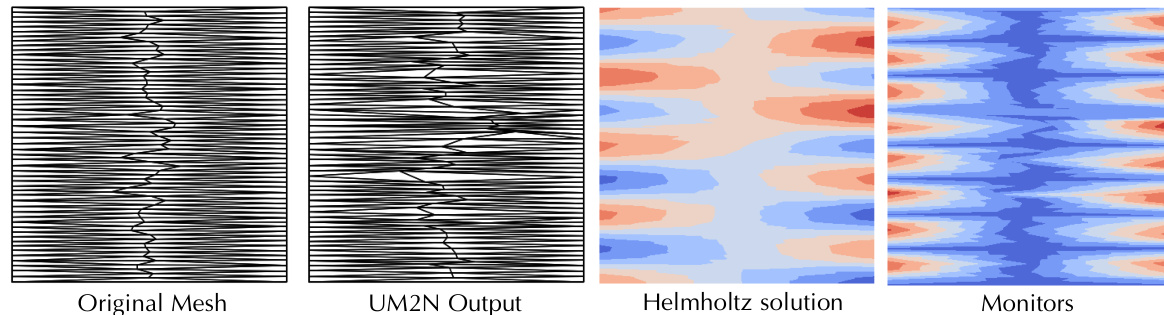
This figure shows the results of applying the UM2N model to a mesh with highly anisotropic elements and several vertices with valence 6, which is considered a low-quality mesh. The figure displays the original mesh, the UM2N output mesh after mesh movement, the solution of an anisotropic Helmholtz problem, and the monitor function used to guide the mesh adaptation. The results demonstrate that UM2N successfully adapts to the anisotropic solution without producing tangled meshes, unlike conventional MA methods that failed to converge or produced tangled meshes.

This figure presents an ablation study on the Swirl case, evaluating the impact of removing key components of the Universal Mesh Movement Network (UM2N) architecture. Three variants were tested: UM2N-w/o-Decoder (removing the GAT Decoder), UM2N-w/o-GT (removing the Graph Transformer), and the full UM2N. The results demonstrate that the complete UM2N model yields superior error reduction compared to the variants with components missing, highlighting the importance of both the decoder and the transformer for optimal performance. The figure shows the error reduction percentages for each model variant and a visual comparison of the resulting meshes.
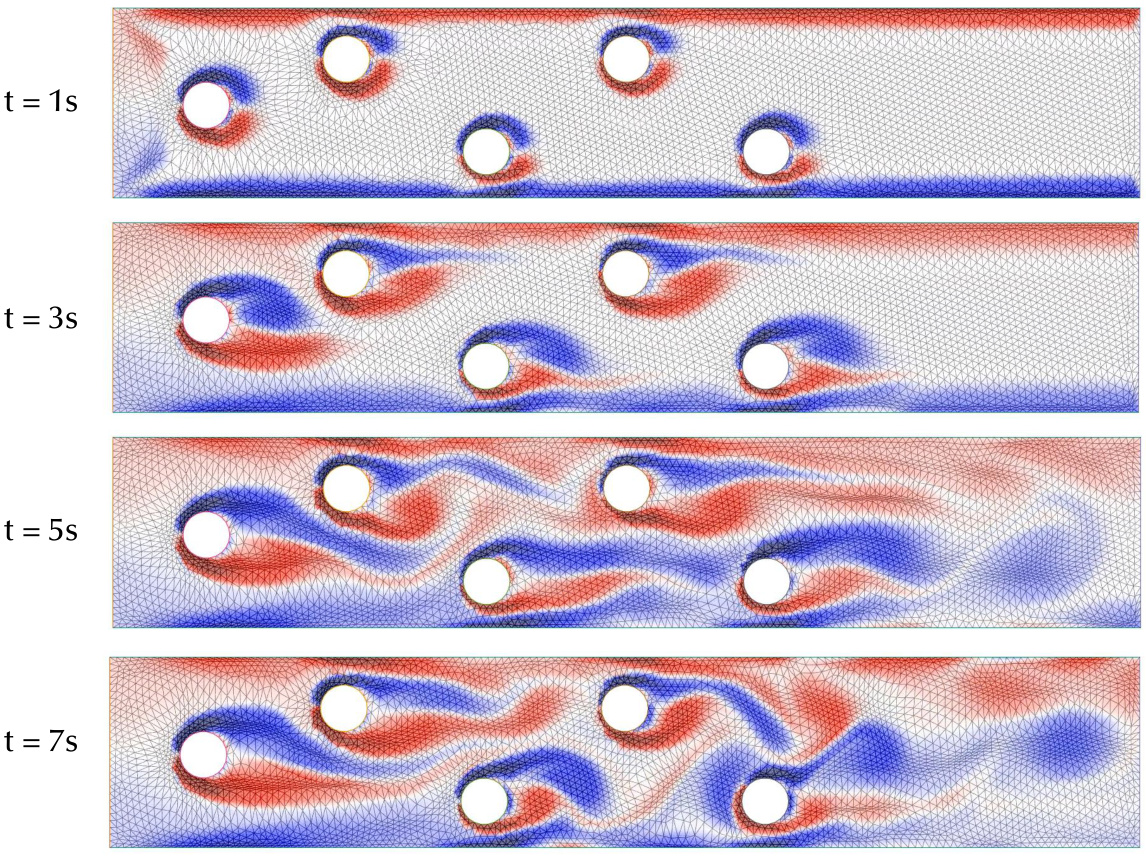
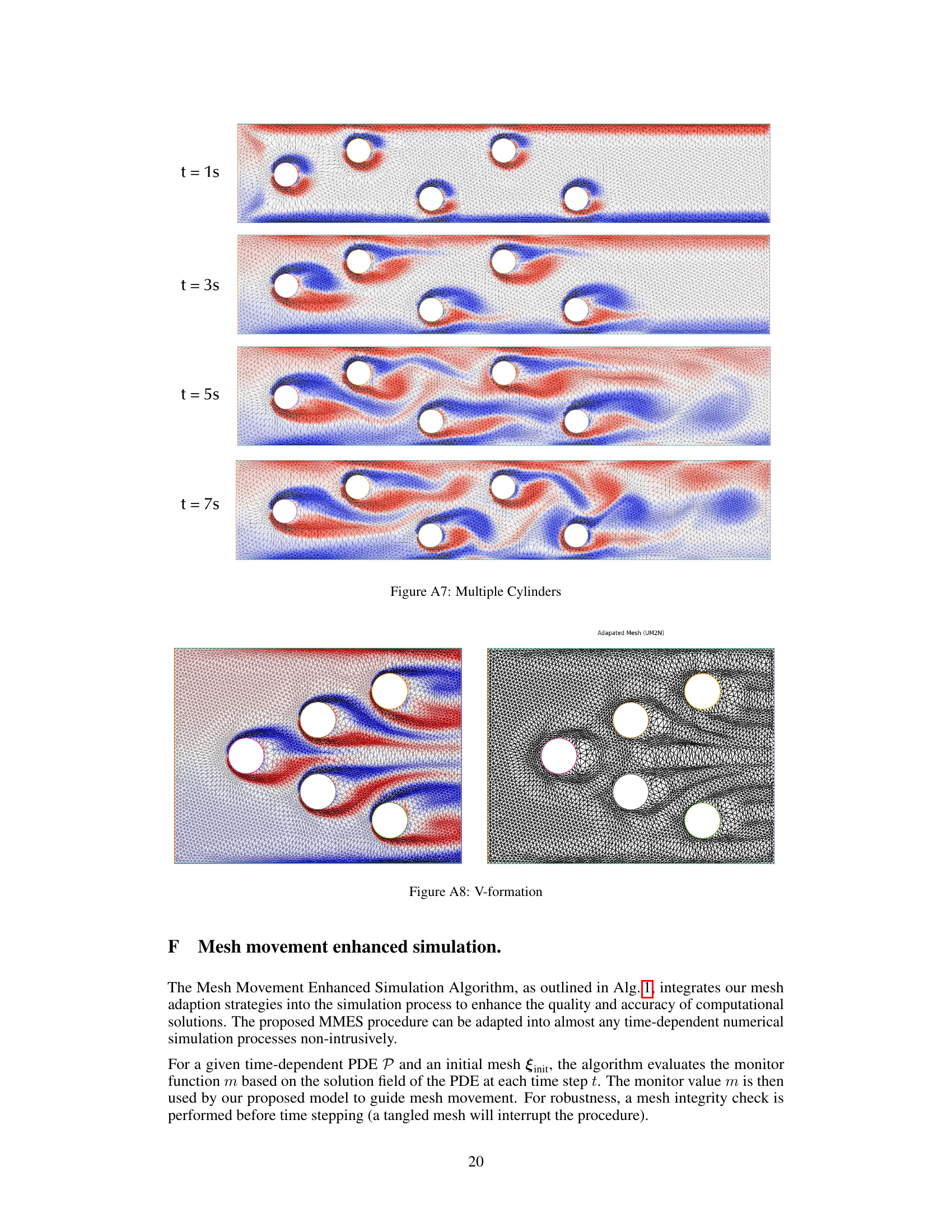
The figure shows a simulation of flow past multiple cylinders. The proposed UM2N can move the mesh, capturing the complex dynamics without mesh tangling. Four time steps are shown (t=1s, t=3s, t=5s, t=7s) illustrating the evolution of the flow patterns around the cylinders.

This figure visualizes the results of a simulation involving multiple cylinders in a channel flow. The images show the flow field (velocity) at different time steps (t=1s, t=3s, t=5s, t=7s). The flow field is colored according to velocity magnitude. The cylinders are represented as white circles. It demonstrates the complex flow patterns and wake formations that occur when multiple cylinders are present.

This figure shows the results of applying the UM2N method to a flow past multiple cylinders scenario. The images display the vorticity field at different times (t=1s, t=3s, t=5s, t=7s) showing the development of vortices and the movement of fluid around the cylinders. This demonstrates the algorithm’s ability to handle complex flow patterns and adapt the mesh accordingly.
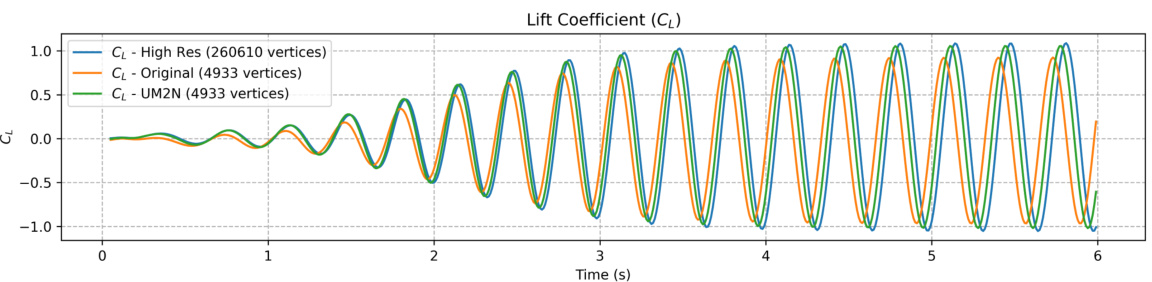
This figure shows the lift coefficient (CL) over time for a flow past a cylinder simulation. Three lines represent the CL calculated using a high-resolution mesh (260,610 vertices), the original mesh (4933 vertices), and the mesh adapted by the UM2N model (4933 vertices). The UM2N-adapted mesh significantly improves the accuracy of the CL calculation, demonstrating the model’s ability to enhance the accuracy of simulations by improving mesh resolution.
More on tables

This table presents the results of ablation studies conducted to evaluate the impact of different design choices on the Universal Mesh Movement Network (UM2N). Specifically, it compares the performance of three variants of UM2N: UM2N-coord (using coordinate loss), UM2N-sol (using PDE solutions as input), and the original UM2N (using element volume loss and monitor functions). The performance is measured by the PDE error reduction ratio (ER) for three different PDE types: Helmholtz, Swirl, and Cylinder. The results show that the original UM2N outperforms the other variants, highlighting the effectiveness of the chosen design choices.

This table quantitatively compares the performance of three mesh movement methods: Monge-Ampère (MA), M2N, and UM2N (the proposed method). The comparison is done across three different scenarios: Swirl, Cylinder, and Helmholtz. For each scenario, the table shows the PDE error reduction ratio (ER) and the computation time. The ER indicates how much the PDE solution error is reduced by using the method compared to a baseline solution on an original, unmodified mesh. ‘Fail’ indicates cases where the mesh movement method failed due to mesh tangling, preventing successful computation.
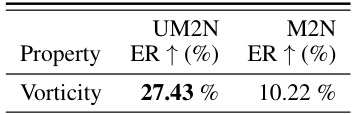
This table presents a quantitative comparison of the performance of the UM2N and M2N models in terms of error reduction (ER) for the vorticity property in a flow-past-a-cylinder simulation. The results show a significant improvement in error reduction by UM2N compared to M2N.
Full paper#