Unitary Convolutions for Learning on Graphs and Groups

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses the instability issues in deep group-convolutional architectures, a critical challenge in various machine learning applications. By proposing and analyzing unitary group convolutions, which enhance stability and prevent over-smoothing, the research opens new avenues for designing more robust and effective deep learning models for structured data. It also provides theoretical guarantees and practical implementation details, making it highly relevant for researchers working with graph neural networks and other group-equivariant models.

Visual Insights

#

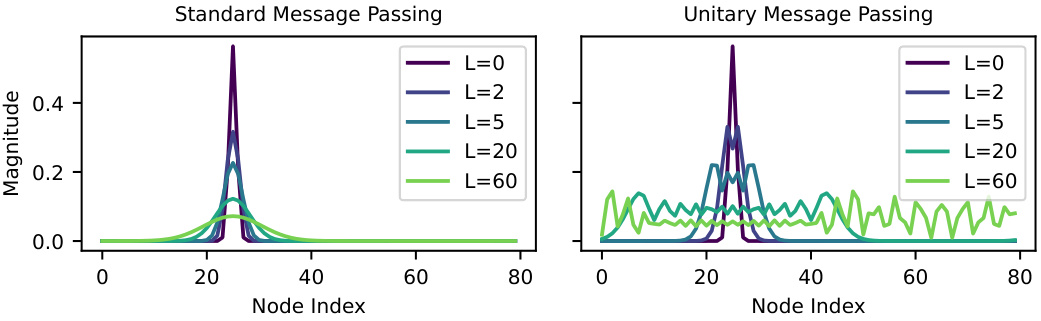
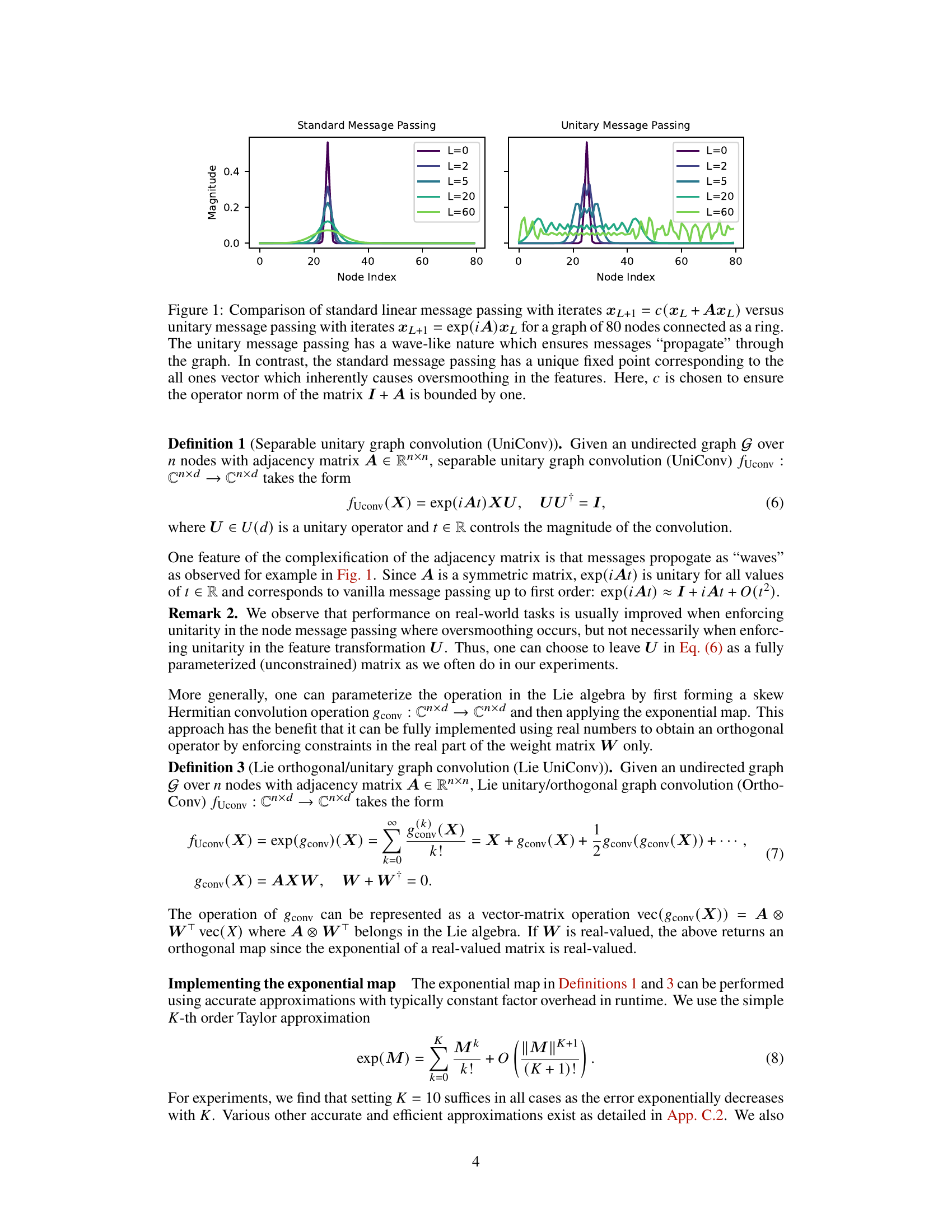
The figure compares standard message passing and unitary message passing on a ring graph with 80 nodes, showing the magnitude of node features after different numbers of iterations (layers). Standard message passing quickly converges to a fixed point (oversmoothing), while unitary message passing maintains wave-like propagation, avoiding this issue. This illustrates the benefit of using unitary convolutions for enhanced stability.

The table compares the performance of two unitary graph convolutional network (GCN) models (UniConv and Lie UniConv) with other state-of-the-art GCNs on three benchmark datasets from the Long Range Graph Benchmark (LRGB): Peptides, COCO, and Pascal VOC. The results show the test accuracy (AP) and mean absolute error (MAE) for the Peptides dataset, and the test F1-score for the COCO and Pascal VOC datasets. The table highlights that the unitary GCN models achieve competitive or superior performance compared to other methods, even with a parameter budget constraint.

In-depth insights

#

Unitary Convolutions

#

The concept of “Unitary Convolutions” in the context of graph neural networks (GNNs) centers on enhancing the stability and performance of deep learning models by using unitary matrices within the convolutional layers. Unitary matrices, by definition, preserve the norm of vectors and are invertible, which addresses the issues of over-smoothing and vanishing/exploding gradients that often plague deep GNNs. Over-smoothing, where node representations converge to a fixed point, is mitigated because unitary operations prevent the collapse of information. The authors propose two variants of unitary graph convolutions: Separable Unitary Convolution and Lie Orthogonal/Unitary Convolution, differing primarily in their parameterization techniques. The theoretical analysis proves that these convolutions avoid over-smoothing, and experimental results on benchmark datasets show competitive performance compared to state-of-the-art GNNs. The extension to general group convolutions further broadens the applicability and stability improvements offered by unitary convolutions beyond the graph domain.

Graph Stability

#

Graph stability, in the context of graph neural networks (GNNs), is a crucial concern because it directly affects the network’s ability to learn effectively. Over-smoothing, where node representations converge and lose their distinctiveness, is a significant challenge that impacts long-range dependency learning. This paper introduces unitary group convolutions to address this problem by ensuring that the linear transformations within the network are norm-preserving and invertible. The theoretical analysis demonstrates how these unitary convolutions prevent over-smoothing by maintaining representation diversity, leading to improved performance on downstream tasks. Unitary graph convolutions are shown to enhance stability during training by avoiding the convergence of node representations and enhancing the learning of long-range dependencies. Empirical results validate these findings with competitive performance against state-of-the-art GNNs, highlighting the importance of unitary transformations for achieving stable and accurate learning on graph-structured data.

GNN Over-smoothing

#

Graph Neural Networks (GNNs) are powerful tools for analyzing graph-structured data, but they suffer from a critical limitation known as over-smoothing. Over-smoothing arises from the iterative nature of GNN message passing: as the number of layers increases, node representations tend to converge, losing their individuality and the crucial distinctions that encode essential information. This convergence leads to homogeneous node embeddings, making it difficult for the network to discriminate between nodes and hindering downstream task performance, especially those involving long-range dependencies. The phenomenon is particularly acute in deep GNNs. Several mitigation strategies exist, including architectural modifications (skip connections, residual connections), and input graph perturbations. However, a principled and theoretically grounded approach is crucial. This often involves careful design of the message-passing mechanism or leveraging specific mathematical properties, such as the use of unitary transformations which preserve norms and distances, to maintain representational diversity and prevent the over-smoothing effect. Ultimately, understanding and addressing over-smoothing is pivotal for unlocking the full potential of deep GNNs in various applications.

Empirical Validation

#

An Empirical Validation section would rigorously assess the claims made about unitary group convolutions. It would present results on various benchmark graph datasets, comparing the performance of models using unitary convolutions against state-of-the-art baselines. Key metrics to include would be classification accuracy, runtime, and potential measures of stability (e.g., eigenvalue distributions, gradient norms). The experimental setup should be clearly described, including data preprocessing, model architecture details, hyperparameter tuning methods, and training procedures. A discussion of statistical significance would be essential, possibly including error bars, confidence intervals, or p-values. The results should be carefully analyzed and interpreted, paying attention to scenarios where unitary convolutions excel or fall short. Addressing potential limitations is crucial, such as the computational cost of unitary operations and the effects on model expressivity. The section should conclude by summarizing the key findings and their implications for advancing graph neural network architectures.

Future Directions

#

The “Future Directions” section of this research paper suggests several promising avenues for future work. Extending unitary graph convolutions to incorporate edge features would broaden their applicability and improve performance. Developing hybrid models that combine unitary and non-unitary layers could result in more robust and versatile GNN architectures. Improving the efficiency of parameterizations and implementations of the exponential map used in unitary operations is another key area for advancement. Approaches that only approximately enforce unitarity could achieve comparable performance gains with better computational efficiency. Finally, exploring the application of unitary convolutions to a wider range of tasks and data domains beyond graph classification and regression, such as tasks involving more general symmetries, and rigorously testing their robustness against adversarial attacks are crucial next steps.

More visual insights

#

More on figures

This figure compares standard message passing with unitary message passing on a ring graph with 80 nodes. It shows how standard message passing quickly converges to a fixed point (oversmoothing), while unitary message passing exhibits wave-like behavior, demonstrating its ability to avoid oversmoothing and propagate information more effectively.

This figure compares standard linear message passing and unitary message passing on a ring graph with 80 nodes. It illustrates how standard message passing converges quickly to a fixed point (oversmoothing), while unitary message passing exhibits a wave-like propagation of information, preventing oversmoothing.

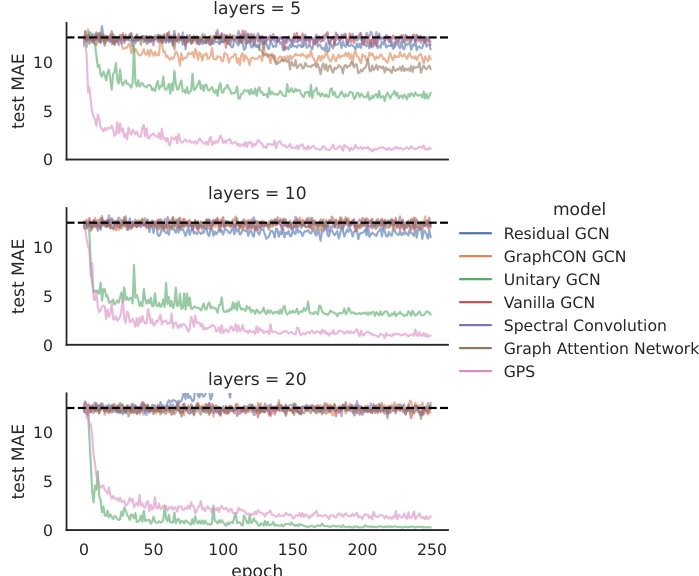
This figure compares the performance of various graph neural network architectures on the MUTAG dataset as the number of layers increases. The x-axis shows the number of layers, and the y-axis shows the test accuracy. The Unitary GCN (U-GCN) maintains its accuracy across the different numbers of layers, while the other architectures (GCN, GIN, GAT) show a significant drop in accuracy with increasing depth, indicating an over-smoothing phenomenon. This highlights the advantage of unitary convolutions in preventing over-smoothing in deep GNNs.

This figure compares standard linear message passing with unitary message passing. It uses a ring graph with 80 nodes to illustrate the difference in how messages propagate. The standard message passing converges to a fixed point (oversmoothing), while unitary message passing shows a wave-like propagation behavior which avoids oversmoothing.

More on tables

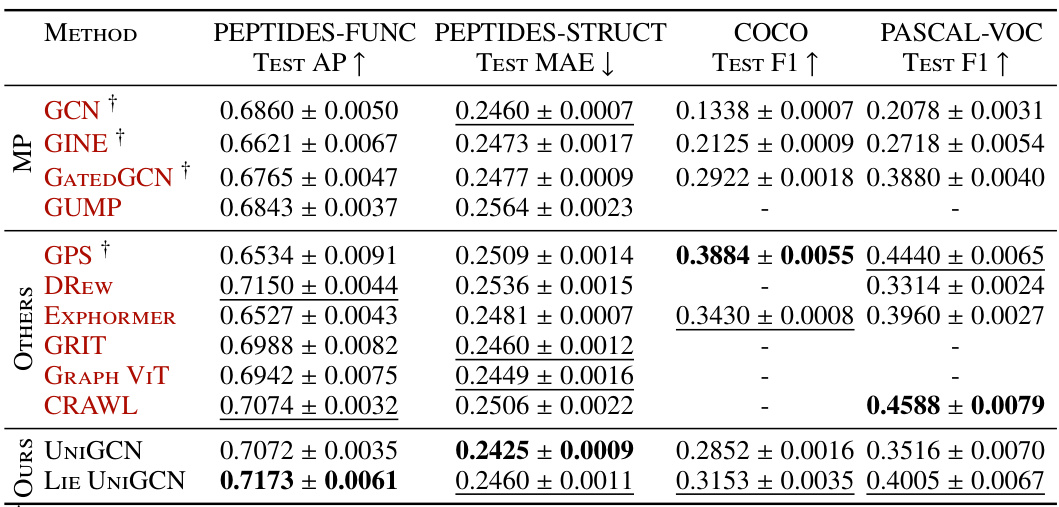
This table compares the performance of two proposed unitary graph convolutional network (GCN) models, UniGCN and Lie UniGCN, against several other state-of-the-art GCN models on four benchmark datasets from the Long Range Graph Benchmark (LRGB) [DRG+22]. The results show test accuracy (AP) and mean absolute error (MAE) for two peptide datasets (Peptides-Func and Peptides-Struct), and test F1 scores for COCO and PASCAL VOC datasets. The table highlights the competitive performance of the proposed unitary models and notes that the models are designed to have a maximum of 500,000 parameters. Details of hyperparameters and training procedures are provided in Appendix G.

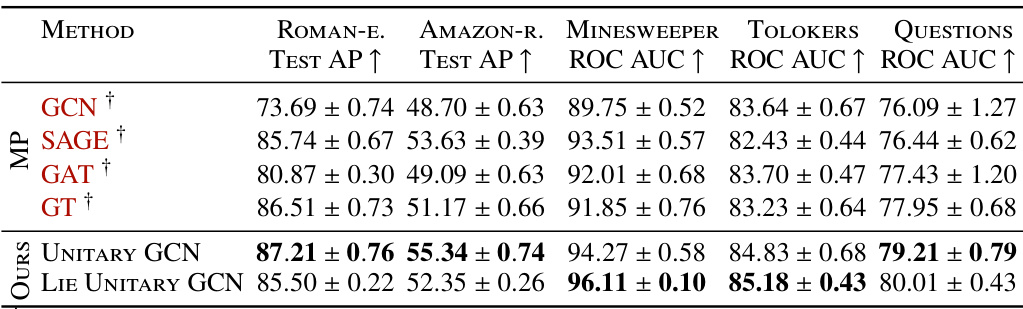
This table compares the performance of Unitary Graph Convolutional Networks (GCNs) using two different types of unitary convolutions (UniConv and Lie UniConv) against other state-of-the-art GNN architectures on several heterophilous graph datasets. Heterophilous datasets are characterized by the presence of nodes with dissimilar labels that are connected together. The table presents the test accuracy, along with confidence intervals, for each method on each dataset. The results demonstrate that the unitary GCN models achieve competitive performance compared to other methods.

The table compares the performance of two proposed unitary graph convolutional networks (UniGCN and LieUniGCN) with other state-of-the-art Graph Neural Networks (GNNs) on several benchmark datasets from the Long Range Graph Benchmark (LRGB). The results show that the proposed unitary GCN models perform competitively with or even surpass the existing methods across several evaluation metrics.

The table compares the performance of two variants of unitary graph convolutional networks (UniConv and Lie UniConv) against other state-of-the-art GNNs on benchmark datasets from the Long Range Graph Benchmark (LRGB). The metrics used are Test AP (Average Precision), Test MAE (Mean Absolute Error), and Test F1 (F1-score). The results highlight the competitive performance of the unitary GCN architectures, especially considering a parameter budget constraint.

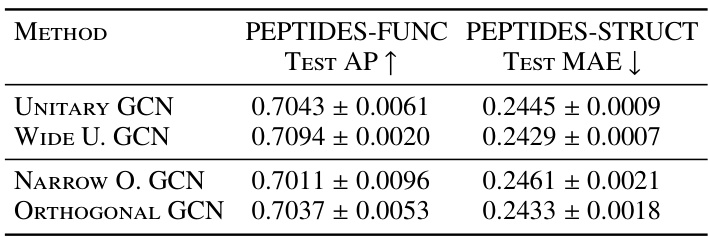
The table compares the performance of Unitary GCN (with Lie UniConv layers) against other Graph Neural Network (GNN) architectures on four datasets from the TUDataset benchmark. The performance metric is Test Average Precision (AP). A ‘Wide Unitary GCN’ is also included, where the number of parameters is adjusted to be comparable to standard GCNs.

This table compares the performance of two variants of unitary graph convolutional networks (UniConv and Lie UniConv) against other state-of-the-art Graph Neural Networks (GNNs) on several benchmark datasets from the Long Range Graph Benchmark (LRGB). The results show the test accuracy and mean absolute error for peptide function classification, peptide structure regression, and node classification tasks on COCO and Pascal VOC datasets. The table highlights the competitive performance of the unitary GCNs, especially considering a parameter budget constraint.

The table compares the performance of two variants of unitary graph convolutional networks (UniConv and LieUniConv) against other state-of-the-art Graph Neural Networks (GNNs) on benchmark datasets from the Long Range Graph Benchmark (LRGB). The results show the test accuracy (AP) and mean absolute error (MAE) for peptide function and structure prediction tasks, and test F1 scores for object detection tasks. The unitary GCN models achieve competitive performance, demonstrating the effectiveness of the proposed method in improving stability and long-range dependency learning.

This table compares the performance of Unitary Graph Convolutional Networks (GCNs) using two different types of unitary convolutions (UniConv and LieUniConv) against other state-of-the-art GCN architectures on four datasets from the Long Range Graph Benchmark (LRGB). The results are presented in terms of Test Average Precision (AP) and Test Mean Absolute Error (MAE) for the Peptides datasets and Test F1 score for the COCO and Pascal VOC datasets. The table highlights that the unitary GCNs achieve competitive performance with other models, while staying within a specified parameter budget.

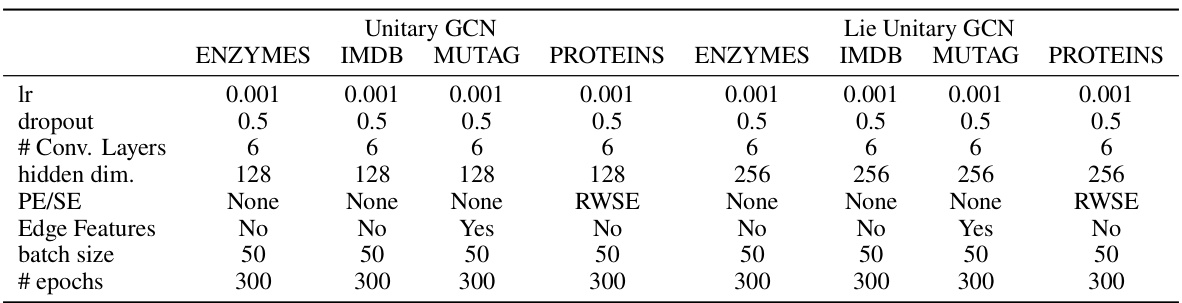
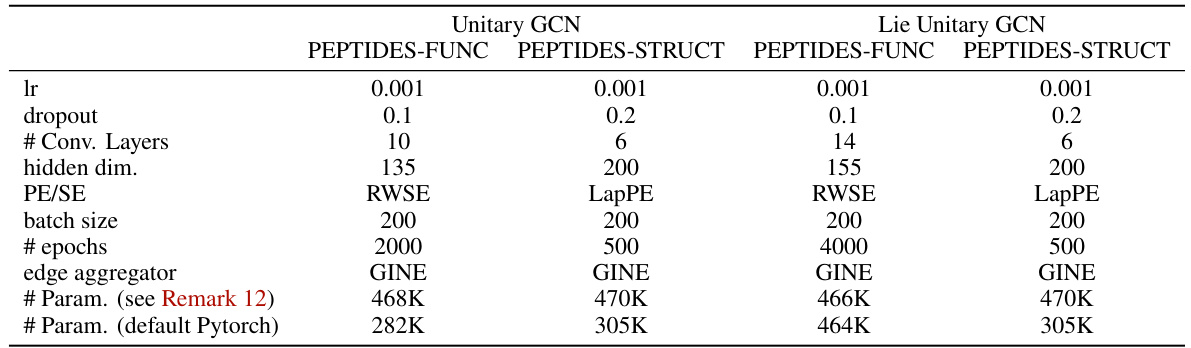
The table shows the hyperparameters used for training different models on the TU datasets. For each dataset (ENZYMES, IMDB-BINARY, MUTAG, PROTEINS), the table lists the learning rate, dropout rate, number of convolutional layers, hidden dimension, positional encoding scheme (PE/SE), whether edge features were used, batch size, and number of epochs. Different hyperparameter settings were used for the unitary GCN and Lie unitary GCN models.

The table compares the performance of Unitary GCN with two different convolution methods (UniConv and Lie UniConv) against other state-of-the-art Graph Neural Network (GNN) architectures on four datasets from the Long Range Graph Benchmark (LRGB). The results show the test accuracy and mean absolute error (MAE) for each model, demonstrating that the Unitary GCN performs competitively with existing models while remaining within a specified parameter budget.

This table compares the performance of Unitary Graph Convolutional Networks (GCNs) with two different types of unitary convolution layers (UniConv and Lie UniConv) against other state-of-the-art GCN architectures on the Long Range Graph Benchmark (LRGB) datasets. The results are presented in terms of test accuracy and mean absolute error (MAE). The table highlights that the Unitary GCN models achieve competitive or better performance than other models, emphasizing the effectiveness of the unitary convolutions in improving the stability and performance of GCNs.

Full paper

#