↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Current computer-aided synthesis planning (CASP) algorithms often struggle with real-world constraints, such as requiring specific starting materials. Existing methods assume the availability of arbitrary building blocks, limiting their practicality. This necessitates more sophisticated algorithms that can effectively navigate the search space while adhering to these constraints. This research addresses these limitations.
The proposed solution, Double-Ended Synthesis Planning (DESP), leverages a bidirectional graph search that interleaves expansions from both the target molecule and the goal starting materials. This ensures constraint satisfaction and improved efficiency. DESP incorporates a goal-conditioned cost network to guide the search, further enhancing its performance. Experiments on multiple benchmarks demonstrate DESP’s superiority over existing approaches, especially in constrained scenarios, highlighting its potential to revolutionize the field of CASP.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computer-aided synthesis planning (CASP) as it introduces a novel bidirectional search algorithm that significantly improves the efficiency and success rate of finding synthetic routes, particularly in constrained real-world scenarios. It also presents new benchmarks and offers insights into the design of goal-conditioned cost networks, paving the way for improved CASP systems.
Visual Insights#

This figure compares single-ended and double-ended search methods for synthesis planning. (a) shows a typical single-ended search where the algorithm explores from the target molecule to arbitrary building blocks until the termination criteria is met. (b) shows the double-ended search used by the DESP algorithm where the search is conducted bidirectionally from both the target molecule and the specified starting material, interleaving expansions to ensure constraint satisfiability, resulting in fewer node expansions.

This table summarizes the characteristics of three benchmark datasets used in the paper to evaluate different synthesis planning algorithms. It shows the number of routes in each dataset, the average percentage of reactions that are in-distribution (i.e., also present in the training set), the percentage of unique reactions (after deduplication), the average number of reactions per route, and the average depth (length of the longest branch) of the routes.
In-depth insights#
Bidirectional CASP#
Bidirectional computer-aided synthesis planning (CASP) represents a significant advancement in retrosynthetic analysis. Traditional CASP approaches often employ a unidirectional search, starting from the target molecule and working backward. A bidirectional approach, however, simultaneously explores pathways from both the target and potential starting materials. This strategy offers several key advantages. First, it can drastically reduce the search space, leading to faster computation times and higher success rates. Second, a bidirectional approach can be particularly beneficial when specific starting materials are preferred, a scenario common in industrial synthesis. By incorporating constraints and incorporating both forward and reverse reactions, bidirectional CASP algorithms are better equipped to navigate the complexity of real-world synthesis. This improvement in efficiency and feasibility makes bidirectional CASP a promising methodology for accelerating drug discovery, materials science and other chemical synthesis applications. The core challenge in implementing bidirectional CASP lies in efficiently integrating forward and backward synthesis models in a way that leverages the strengths of each approach, while effectively managing computational costs and memory constraints.
Goal-Conditioned Cost#
The concept of a ‘Goal-Conditioned Cost’ network within the context of computer-aided synthesis planning (CASP) is a significant advancement. It addresses limitations of traditional CASP methods by incorporating expert knowledge and biasing the search process towards desirable starting materials. Instead of solely relying on generic cost functions evaluating molecule synthesizability from readily available building blocks, this approach introduces a cost function specifically trained to estimate the cost (or distance) between molecules conditioned on a specific goal. This goal-conditioning allows the algorithm to prioritize pathways that leverage expert-specified starting points, improving efficiency and the likelihood of discovering preferred synthetic routes. The network’s learning process likely involves supervised learning, using expert-designed synthetic pathways as training data. This approach presents a powerful way to integrate domain expertise into algorithmic synthesis planning, opening the door to more efficient and effective solutions for complex molecular synthesis problems. The offline training nature offers scalability, making it applicable to large chemical reaction databases and various goal molecules, while maintaining the speed and efficiency of the search.
DESP Algorithm#
The Double-Ended Synthesis Planning (DESP) algorithm is a novel approach to computer-aided synthesis planning that addresses the limitations of traditional methods by incorporating starting material constraints. DESP employs a bidirectional search strategy, interleaving expansions from both the target molecule and the specified starting material(s). This bidirectional approach ensures constraint satisfiability and improves efficiency by guiding the search toward feasible solutions. A crucial component of DESP is the goal-conditioned cost network, which learns to estimate the synthetic distance between molecules, biasing the search toward expert goals. The algorithm’s effectiveness is demonstrated by its improved solve rates and reduced search expansions compared to single-ended methods on multiple benchmark datasets. DESP’s flexibility is showcased by its compatibility with existing one-step retrosynthesis models, leveraging their advances to enhance its performance. The algorithm’s two variations, F2E and F2F, explore different strategies for interleaving search directions, each exhibiting strengths and weaknesses in terms of solution length and computational efficiency.
Benchmark Datasets#
The selection and characteristics of benchmark datasets are crucial for evaluating the performance of computer-aided synthesis planning (CASP) algorithms. The USPTO-190 dataset, while widely used, suffers from redundancies and out-of-distribution reactions, limiting its effectiveness for rigorous evaluation. The authors address this limitation by introducing two new datasets, Pistachio Reachable and Pistachio Hard, derived from the Pistachio database. These datasets offer advantages by including reactions that are more representative of real-world synthesis scenarios and exhibiting a larger proportion of unique reactions compared to USPTO-190. This improved dataset composition allows for a more robust and reliable assessment of CASP algorithm performance, particularly in the context of starting material constraints, which is the primary focus of the proposed DESP algorithm. The authors’ thoughtful creation of these datasets serves as a significant contribution, setting a new standard for CASP benchmarking and enabling fairer comparisons of future algorithms.
Future Directions#
Future research could explore several promising avenues. Improving the accuracy and efficiency of the one-step retrosynthesis models is crucial, as DESP’s performance directly depends on them. Investigating alternative bidirectional search algorithms or incorporating reinforcement learning could enhance DESP’s ability to find optimal synthesis routes. Extending DESP to handle more complex reaction types (e.g., organometallic reactions, photochemical reactions) would expand its applicability. A deeper exploration of F2E vs. F2F search strategies, and their applicability to various problem instances, would provide valuable insights into algorithm design. Finally, applying DESP to specific domains such as sustainable chemistry or the synthesis of complex natural products, could showcase the algorithm’s versatility and impact.
More visual insights#
More on figures

This figure shows the DESP algorithm’s workflow. (a) illustrates the algorithm’s bidirectional search process between the target and starting material, using a combination of top-down retrosynthesis and bottom-up synthesis. Node evaluation considers both the traditional cost (Vm) and the newly introduced synthetic distance (Dm). Two variations, F2E and F2F, are depicted, differing in how the opposing graph is used to guide the search. (b) details the one-step expansion procedures for both retro and forward synthesis, highlighting the use of classifiers to rank reaction templates and k-NN search for building blocks.

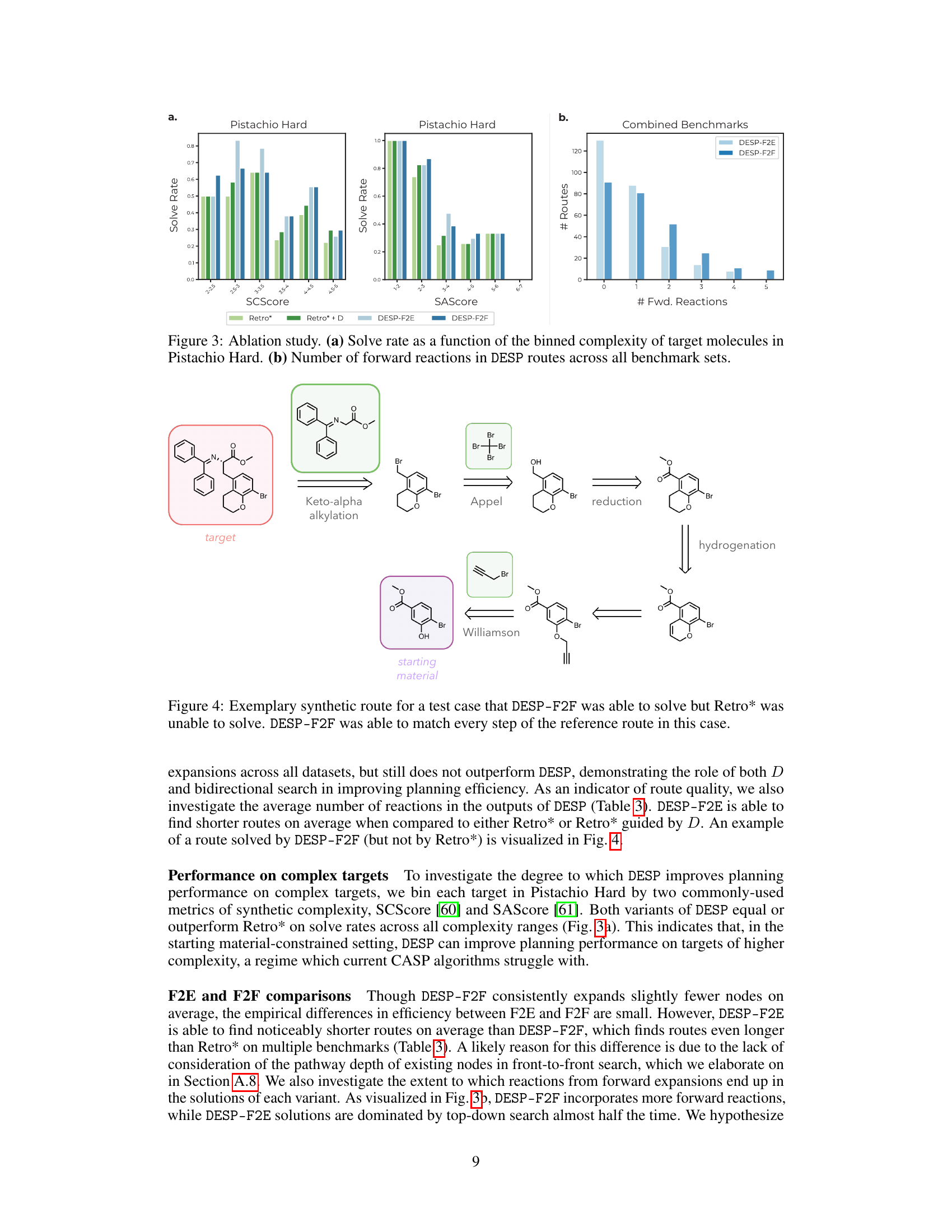
This figure presents the results of an ablation study to evaluate the impact of the synthetic distance (D) and bidirectional search on the performance of the proposed Double-Ended Synthesis Planning (DESP) algorithm. Panel (a) shows the solve rates of different methods (Retro*, Retro*+D, DESP-F2E, DESP-F2F) as a function of the target molecule’s complexity (binned SCScore and SAScore values) for the Pistachio Hard dataset. Panel (b) shows the distribution of the number of forward reactions across all benchmark datasets for DESP-F2E and DESP-F2F, illustrating how the two approaches differ in their utilization of forward reactions.
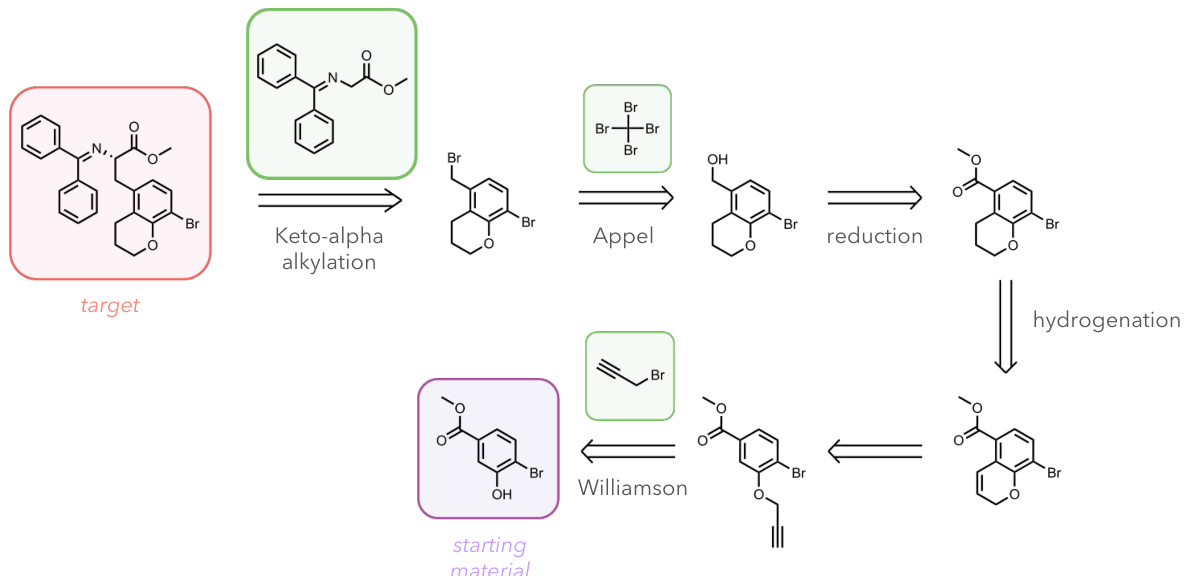
This figure shows an example of a synthetic route successfully found by DESP-F2F but not by Retro*. It highlights DESP’s ability to find a synthetic route that matches the expert’s route step-by-step by leveraging both forward and backward searches, which is a capability that Retro*, a single-ended search algorithm, lacks.
This figure compares single-ended and double-ended search methods in the context of synthesis planning. Panel (a) shows a typical single-ended approach, where the search starts from an arbitrary building block and aims to reach a target molecule. Panel (b) illustrates the double-ended approach of the DESP algorithm, which simultaneously searches forward from a specified starting material and backward from the target molecule, interleaving expansions from both ends to satisfy the constraints and often finding solutions more efficiently.

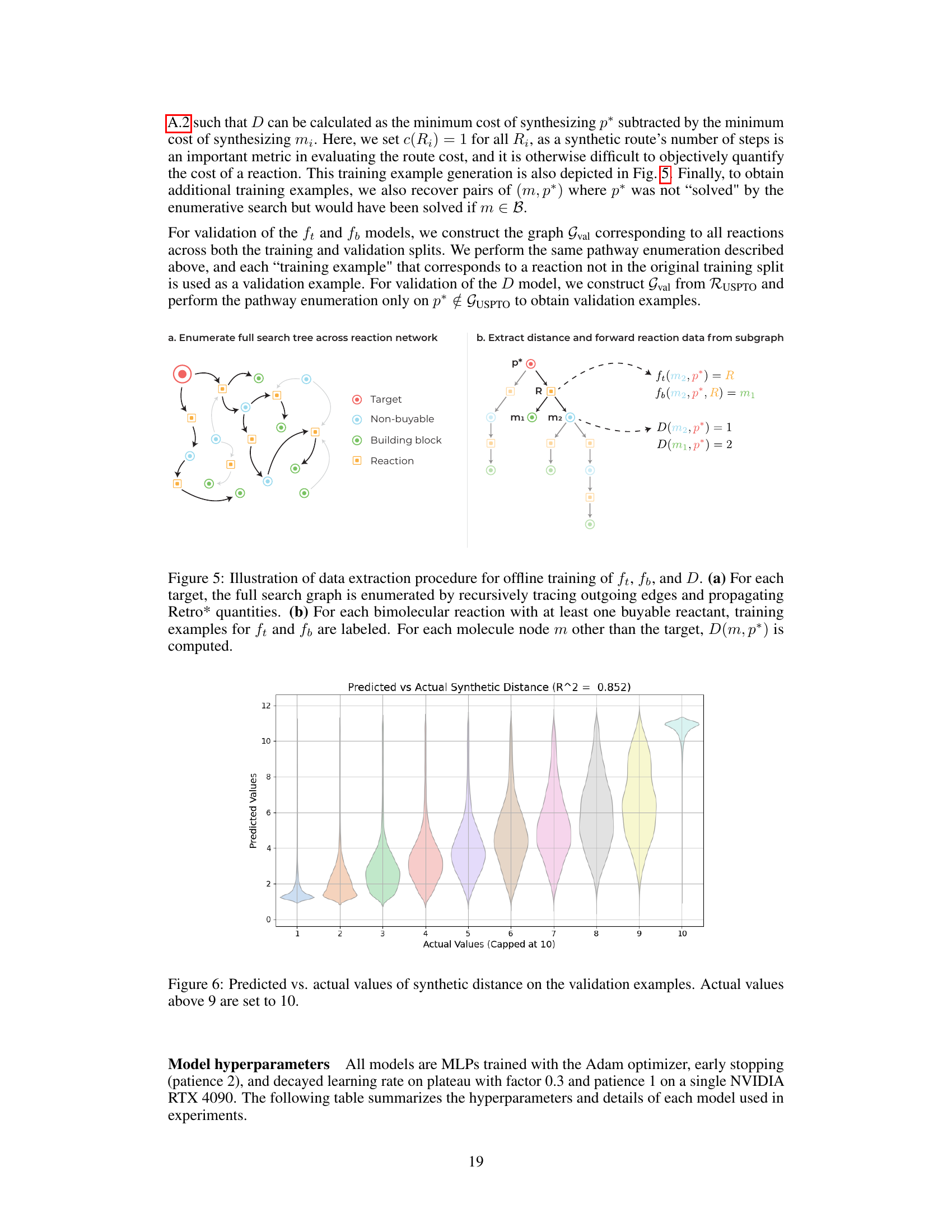
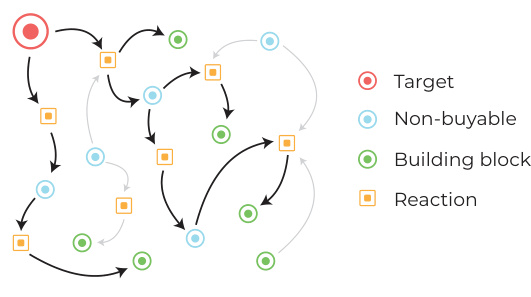
This figure illustrates the process of extracting training data for three different models (ft, fb, and D) used in the Double-Ended Synthesis Planning (DESP) algorithm. Panel (a) shows how the full search graph is traversed to find all possible pathways from the target molecule to building blocks. During this traversal, various metrics are calculated and stored. Panel (b) focuses on extracting training data specifically for bimolecular reactions, where the models learn to predict the reaction and resulting molecules, given starting materials and a reaction template. In both cases, crucial values for synthetic distance are also calculated and used as training labels to help the models improve their estimates of the cost and feasibility of reactions.
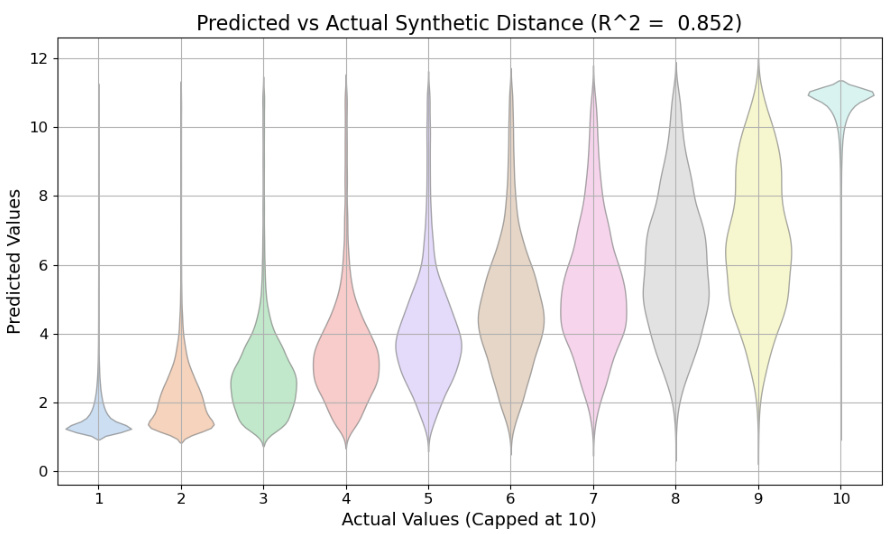
This figure shows a violin plot comparing the predicted synthetic distance values against the actual values on a validation set. The synthetic distance metric, calculated using a goal-conditioned cost network, estimates the cost of synthesizing a molecule from a specific starting material. The plot illustrates the distribution of predicted and actual values, demonstrating a strong correlation between the predicted and actual synthetic distances with an R-squared value of 0.852. The actual values exceeding 9 are capped at 10 to improve the visualization of the distribution.

This figure illustrates the DESP algorithm, showing the evaluation of top nodes and how synthetic distance is calculated for both F2E and F2F search strategies. It also provides a detailed overview of the one-step expansion procedures used in the algorithm.

This figure illustrates the DESP algorithm, showing how it evaluates top nodes based on both Vm and Dm. It also shows the one-step expansion procedures for both top-down and bottom-up search strategies.

This histogram shows the distribution of the number of reactions in the synthetic routes of the Pistachio Reachable dataset. The x-axis represents the number of reactions, and the y-axis represents the number of routes with that many reactions. The dataset consists of 150 synthetic routes that satisfy specific constraints, such as no reactions being present in the training set, no reactions being shared between any routes, and all reactions being within the top 50 proposals of a single-step retrosynthetic model. The data shows a relatively even distribution, with the most frequent number of reactions being around 7 or 8.
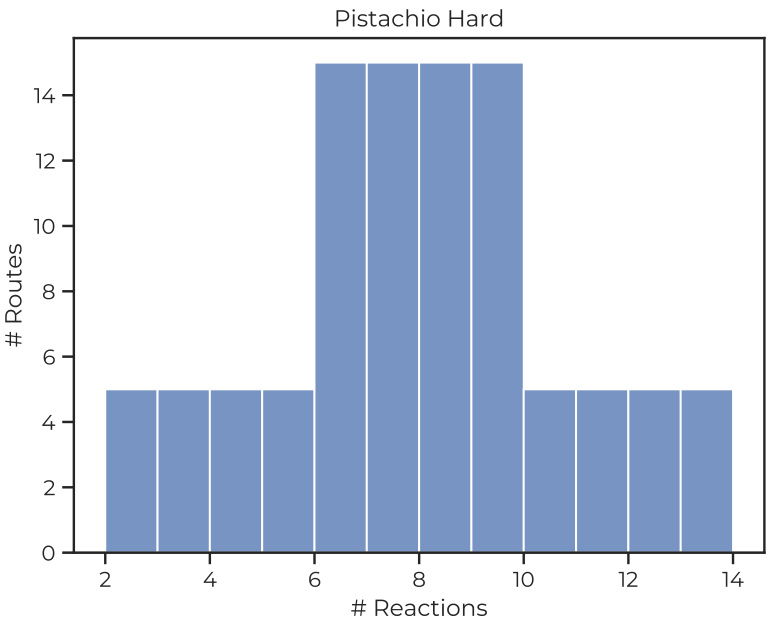
This histogram shows the distribution of the number of reactions in the synthetic routes of the Pistachio Reachable dataset. The x-axis represents the number of reactions, and the y-axis represents the number of routes with that many reactions. The distribution appears relatively uniform, with most routes having between 4 and 8 reactions.
More on tables

This table summarizes the performance of different synthesis planning algorithms on three benchmark datasets (USPTO-190, Pistachio Reachable, and Pistachio Hard) with starting material constraints. It shows the solve rate (percentage of successful synthesis plans) and the average number of search expansions (N) needed to find a solution for each algorithm at different expansion limits (100, 300, and 500). A lower N value indicates better efficiency. The algorithms compared include baseline methods (random search, BFS, MCTS, Retro*, GRASP, Bi-BFS) and variants of the proposed DESP algorithm (DESP-F2E, DESP-F2F).
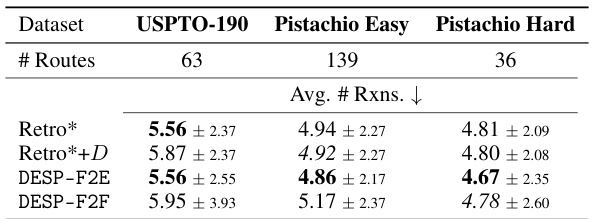
This table presents the average number of reactions (± standard deviation) in the synthetic routes generated by different algorithms. The comparison is made only across the (p*, r*) pairs that were successfully solved by all methods, providing a focused analysis of the route efficiency for comparable scenarios.

This table summarizes the characteristics of three benchmark datasets used in the paper to evaluate the performance of different synthesis planning algorithms. For each dataset, it provides the number of routes, the average percentage of reactions that are in-distribution (i.e., predicted by the retro model), the percentage of unique reactions (after deduplication), the average number of reactions per route, and the average depth of the longest path within each route. These metrics offer a comprehensive overview of the complexity and characteristics of the datasets used to assess the algorithms.

This table summarizes the characteristics of three benchmark datasets used in the paper to evaluate the performance of different synthesis planning algorithms. It shows the number of routes, the average percentage of reactions within the top 50 predictions of the retrosynthetic model that are also present in the ground truth, the percentage of unique reactions across all routes, the average number of reactions per route, and the average depth of the longest reaction path within each route for each dataset.

This table summarizes the characteristics of three benchmark datasets used in the paper to evaluate the performance of the proposed DESP algorithm and other baseline methods. It shows the number of routes, the average percentage of reactions that were already in the dataset’s retro-model’s top 50 predictions, the ratio of unique reactions to all reactions in the datasets, the average number of reactions per route and the average depth of each route. These metrics provide an overview of the complexity and characteristics of each dataset and helps to contextualize the results reported for the different algorithms.
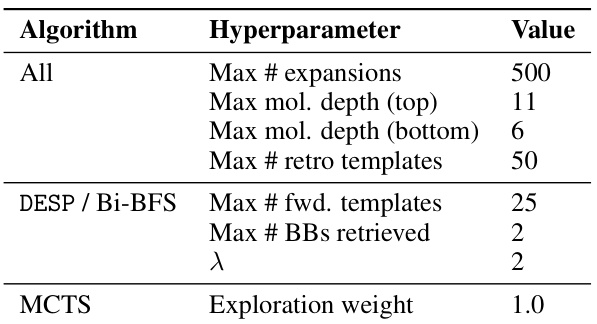
This table summarizes the hyperparameters used for all the different algorithms evaluated in the paper. These hyperparameters control various aspects of the search process, such as the maximum number of expansions allowed, the maximum depth of the search graphs, and the number of templates and building blocks considered during the search.

This table summarizes the performance of various synthesis planning algorithms on three benchmark datasets (USPTO-190, Pistachio Reachable, and Pistachio Hard) under starting material constraints. It shows the solve rate (percentage of target molecules successfully synthesized within a given expansion budget), and the average number of node expansions (N) required to achieve that solve rate for each algorithm. The maximum expansion budget was set to 500.
Full paper#