↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Traditional diffusion models rely on fixed diffusion processes, which may be suboptimal for specific datasets. This paper explores learning the diffusion process from data to improve log-likelihood estimation. A common belief was that the Evidence Lower Bound (ELBO) is invariant to the choice of the noise process in the model, however, this paper shows that this is false and introduces a new concept, the multivariate learned adaptive noise (MuLAN) which makes use of this.
MuLAN leverages Bayesian inference by viewing the diffusion process as an approximate variational posterior. It learns a multivariate noise schedule that is adaptive to the input data, applying different noise rates to various parts of an image. Empirical results on CIFAR-10 and ImageNet show that MuLAN achieves state-of-the-art density estimation and significantly reduces training steps, thereby demonstrating the effectiveness of the learned adaptive noise approach. It dispels a common belief in the field and achieves state-of-the-art results.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generative models and density estimation because it challenges existing assumptions, proposes a novel method for learning the diffusion process, and demonstrates significant performance gains. It opens new avenues for improving likelihood estimation and developing more efficient and adaptable diffusion models.
Visual Insights#
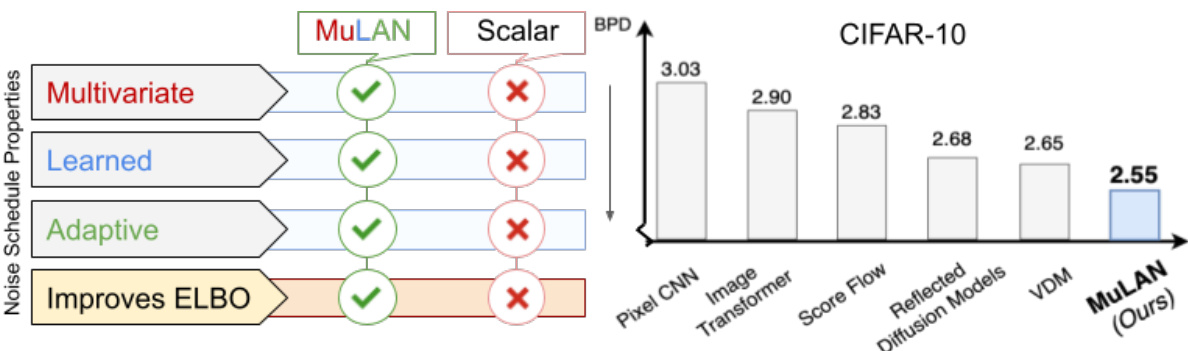
This figure compares the properties of different noise schedules, specifically focusing on the multivariate learned adaptive noise (MULAN) schedule. The left side shows a table summarizing the properties of different schedules like MULAN, scalar, learned, and adaptive, highlighting whether they are multivariate, learned, adaptive, and improve the evidence lower bound (ELBO). The right side presents a bar chart illustrating the likelihood (measured in bits per dimension or BPD) achieved by various diffusion models on the CIFAR-10 dataset without data augmentation. The chart shows that MULAN achieves a state-of-the-art likelihood compared to other models.

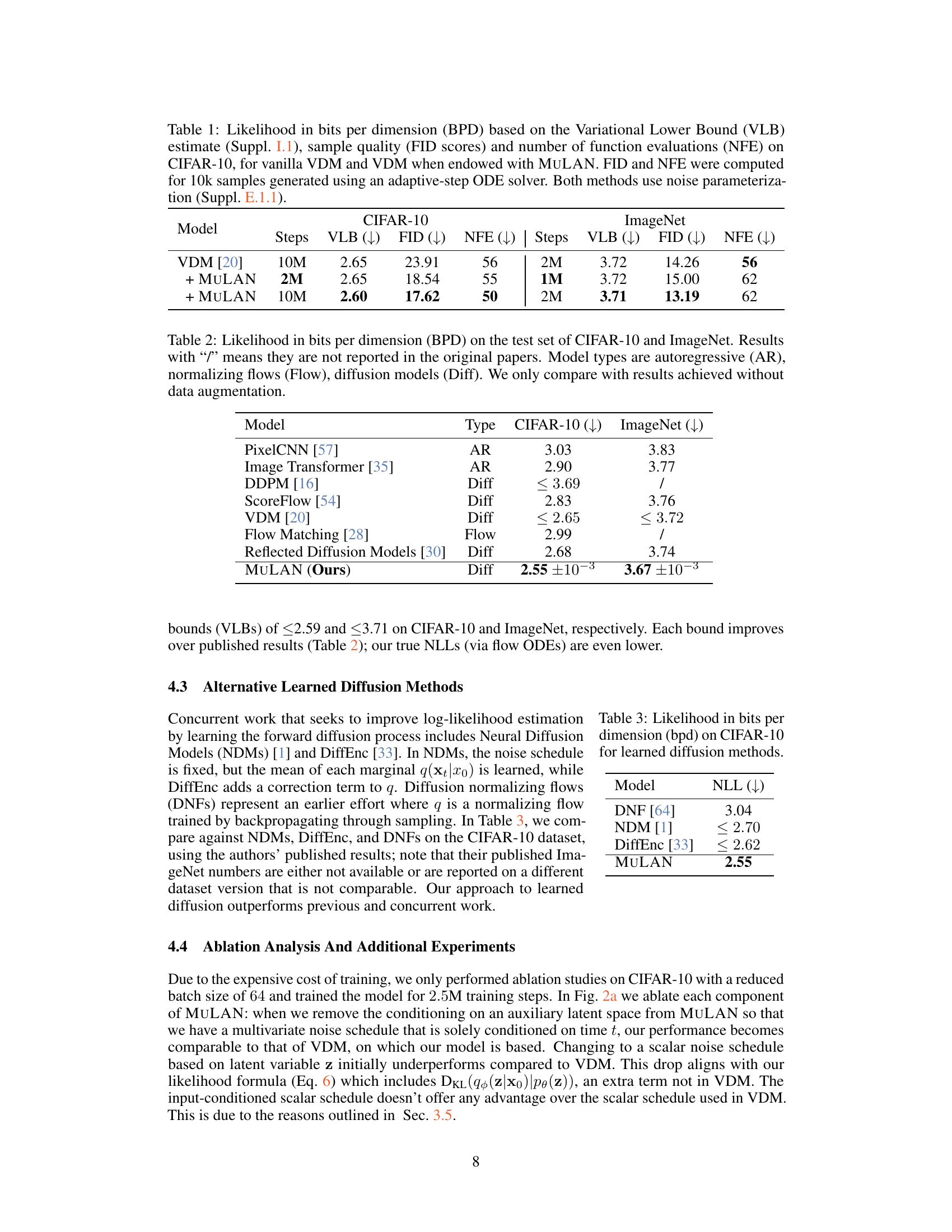
This table compares the performance of the vanilla VDM model with the VDM model enhanced by MULAN. It presents likelihood (VLB), sample quality (FID), and the number of function evaluations (NFE) for both models on the CIFAR-10 dataset. The results highlight the improvements in likelihood and sample quality achieved by incorporating MULAN, while showing the computational efficiency gains (fewer steps needed to reach similar performance).
In-depth insights#
Learned Diffusion#
The concept of “Learned Diffusion” in generative modeling represents a significant departure from traditional diffusion models. Instead of relying on pre-defined diffusion processes rooted in physics or mathematics, learned diffusion models leverage machine learning to optimize the diffusion process itself. This involves learning parameters that govern how data transitions to noise and back, enabling greater flexibility and potentially improved performance. The core advantage lies in the ability to adapt the diffusion process to specific datasets, leading to tighter lower bounds on the likelihood and more accurate density estimation. While this approach introduces challenges such as increased computational complexity and the need for careful regularization, the potential gains in terms of sample quality and model efficiency are substantial. The success of learned diffusion hinges on the ability to effectively learn a diffusion process that closely approximates the true data distribution, thereby making it a very active and promising area of research in generative AI.
Adaptive Noise#
The concept of ‘adaptive noise’ in diffusion models signifies a paradigm shift from traditional fixed noise schedules. Instead of applying noise uniformly across an image, adaptive noise adjusts the noise level based on the characteristics of the data itself. This context-awareness allows the model to better capture the nuances of the data distribution, leading to enhanced performance in tasks like density estimation and sample generation. The adaptive process, as explored in the research paper, likely involves a learned mechanism, possibly a neural network, that dynamically determines the appropriate noise level for each pixel or region based on its features or context. This data-driven approach contrasts with the fixed schedules that treat all pixels equally, thereby improving the efficiency and effectiveness of the learning process. Learning the noise schedule simultaneously with the denoising network is a key challenge, involving a delicate balance between optimizing the ELBO and preventing the model from overfitting the data’s specific noise characteristics. The success of the approach depends on the ability of the learned mechanism to generalize well and effectively adapt to unseen data.
ELBO Invariance#
The concept of ELBO invariance in diffusion models is a crucial one, and the paper challenges the widely held assumption that the evidence lower bound (ELBO) is invariant to the choice of the noise process. Previous works often assumed ELBO invariance, which simplifies optimization but potentially limits performance. This paper’s key contribution lies in demonstrating that this invariance only holds for simple, univariate Gaussian noise processes. By introducing multivariate learned adaptive noise (MULAN), which applies noise at different rates across an image, the authors show that the ELBO is no longer invariant, leading to improved log-likelihood estimation. This finding underscores the importance of carefully considering the noise schedule and the optimization objective in diffusion models. MULAN’s adaptive noise process effectively bypasses the limitations imposed by ELBO invariance, achieving state-of-the-art results in density estimation on benchmark datasets.
CIFAR-10/ImageNet#
The section ‘CIFAR-10/ImageNet’ in this research paper likely details the experimental evaluation of a proposed model on the CIFAR-10 and ImageNet datasets. These are standard benchmark datasets in image processing, offering diverse image content and complexities, making them ideal for assessing a model’s generalization capabilities. The results presented would likely compare the model’s performance (perhaps using metrics like bits-per-dimension (BPD) for density estimation and Fréchet Inception Distance (FID) for sample quality) against other state-of-the-art models. The choice of these datasets is crucial, indicating a focus on demonstrating the model’s effectiveness on widely-used and challenging visual data. High performance on both datasets would strongly support the paper’s claims of improved accuracy and efficiency. We can expect the authors to provide a detailed breakdown of the results, potentially showing variations in performance across different image classes or subsets of data. Detailed analysis of the results on CIFAR-10 and ImageNet would be a key element in evaluating the overall contribution of the research. The authors may also discuss the computational resources required for training and evaluation on these datasets, highlighting any improvements in efficiency achieved by their proposed method.
Future Work#
The paper’s lack of a dedicated ‘Future Work’ section is notable. However, implicit future directions are suggested. Improving sample quality is a clear next step, as the focus on density estimation sometimes sacrifices visual fidelity. Investigating the learned noise schedule’s interpretability is crucial; understanding why and how it produces improved likelihoods could reveal fundamental insights into the diffusion process itself. Extending MULAN to other modalities beyond images is also plausible, potentially through modifications to the underlying U-Net architecture. Exploring the impact of diverse training strategies and architectural improvements to enhance the computational efficiency, particularly given the method’s current limitations on training time, would be of value. Finally, application to downstream tasks needing high-quality density estimates such as compression and semi-supervised learning should be prioritized to showcase the algorithm’s practical benefits.
More visual insights#
More on figures
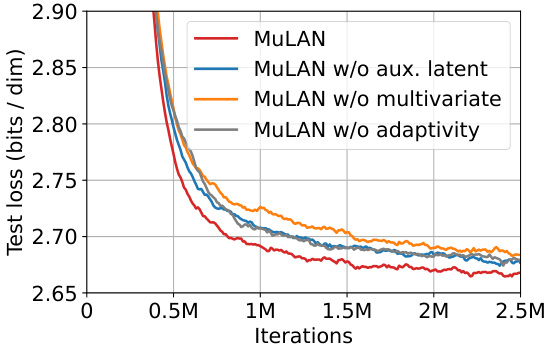
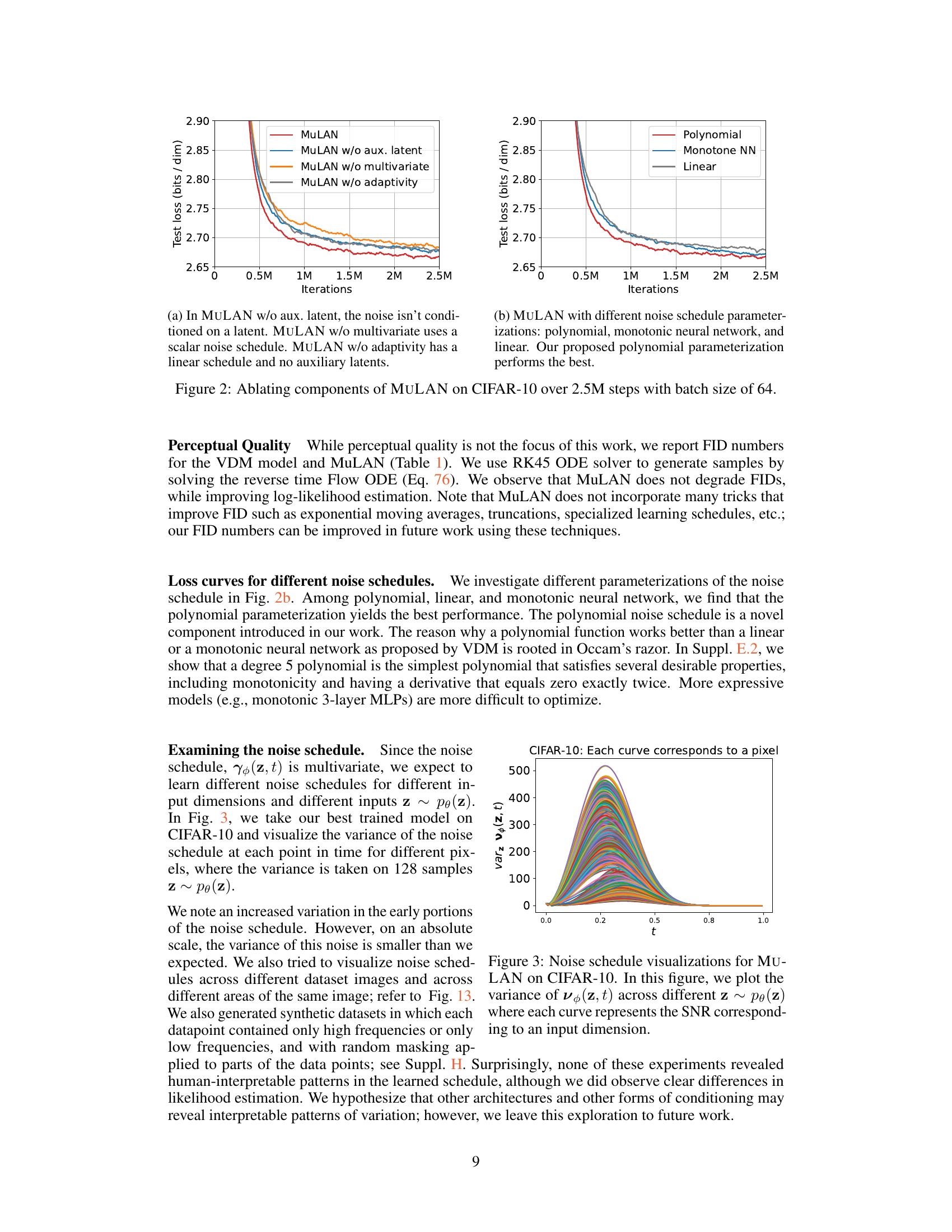
This figure shows the ablation study on CIFAR-10 dataset to evaluate the impact of different components of the MULAN model. Four variants of the model are compared: 1. MULAN: The full model with all components (multivariate, learned, adaptive). 2. MULAN w/o aux. latent: The model without auxiliary latent variables. 3. MULAN w/o multivariate: The model using a scalar noise schedule instead of multivariate. 4. MULAN w/o adaptivity: The model using a linear noise schedule instead of an adaptive noise schedule. The plot shows the test loss (in bits per dimension) over 2.5 million training iterations. It demonstrates that all components of MULAN contribute to its improved performance.
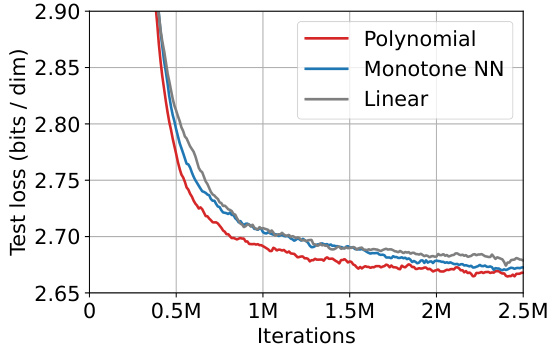
This figure shows the ablation study of MULAN on CIFAR-10 dataset. The left subplot shows the impact of removing different components of MULAN on the test loss. Removing the multivariate property, the adaptive property, or the auxiliary latent variable all lead to a significant increase in the test loss. The right subplot compares different noise schedule parameterizations (polynomial, monotonic neural network, and linear). The polynomial parameterization performs the best, showcasing the effectiveness of this specific design choice in improving performance.
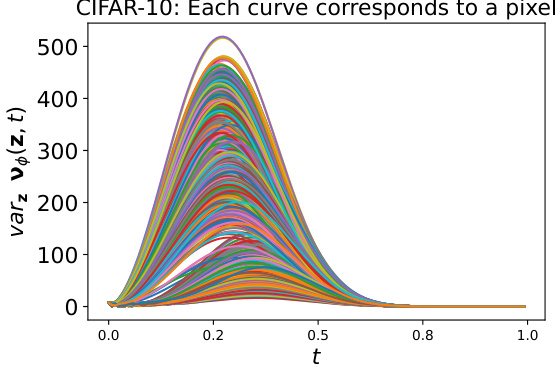
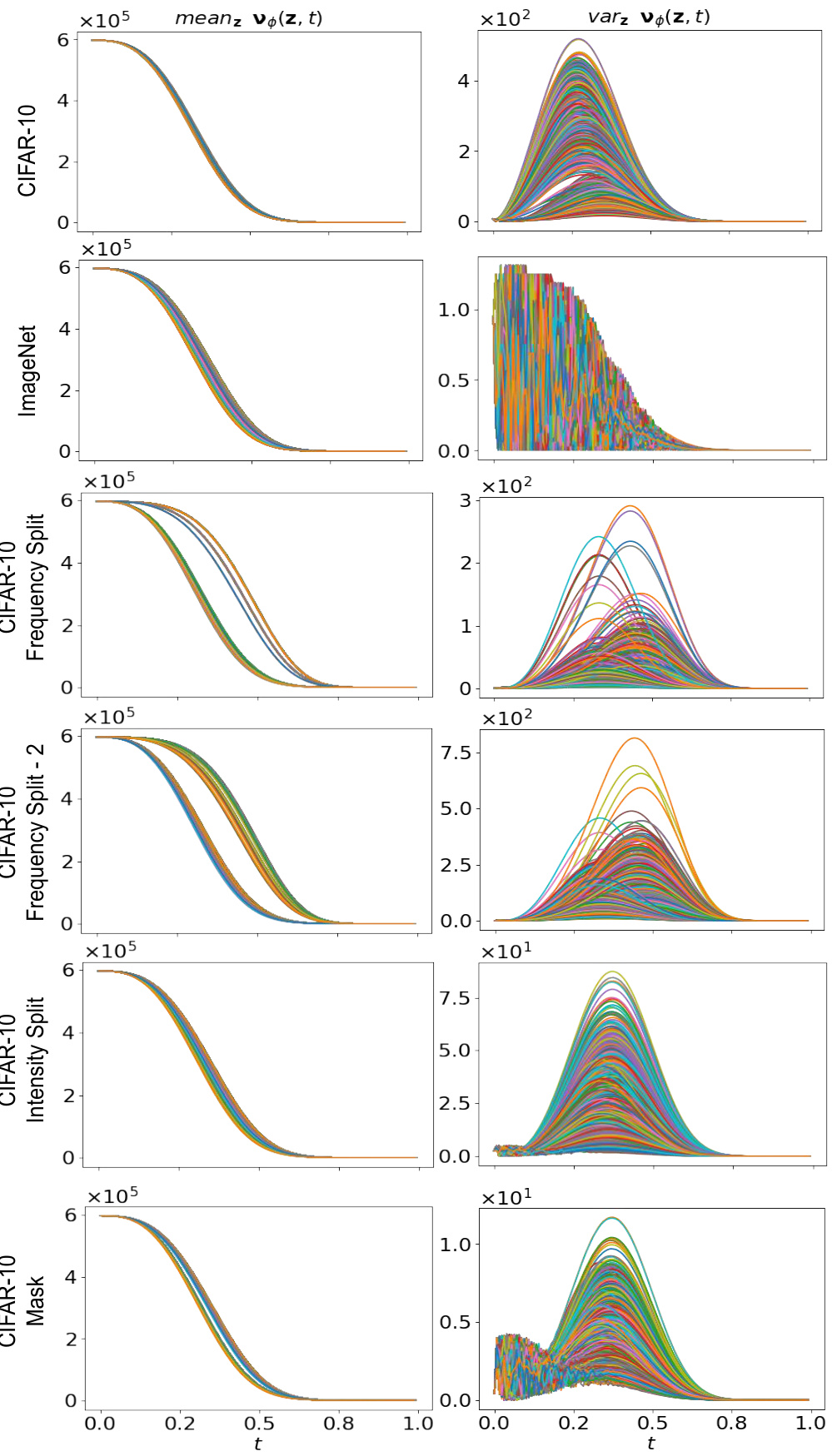
The figure visualizes the variance of the learned noise schedule (SNR) across different latent variables (z) and time steps (t) for MuLAN on the CIFAR-10 dataset. Each curve represents the variance of the SNR for a specific pixel across different latent variables. The plot shows how the variance changes over time, offering insights into the adaptive nature of the noise injection process in MuLAN. It helps illustrate how MuLAN injects noise at different rates across the image, adapting to spatial variations and influencing the model’s learning process.
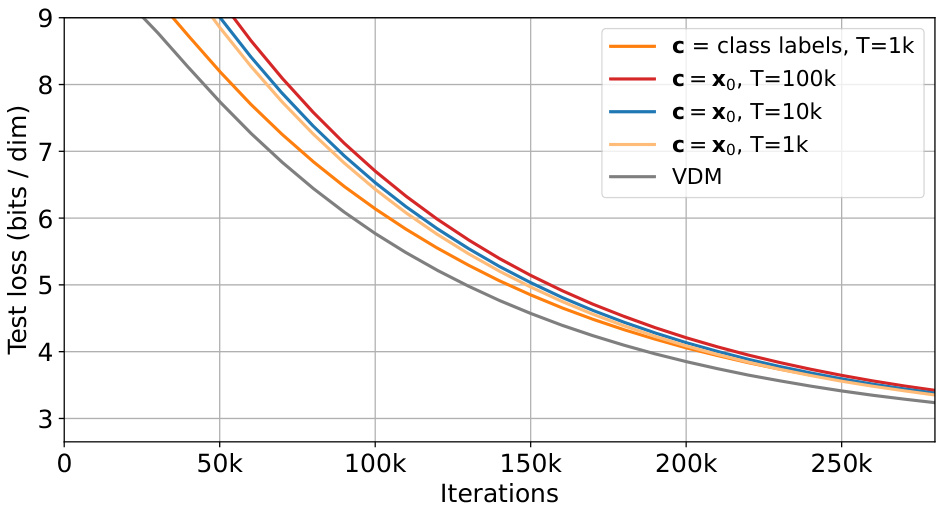
This figure shows the test loss (bits/dim) over iterations for different settings of the diffusion process. The settings include using class labels or the input image itself as context (c), and varying the number of timesteps (T). The results show that using the input image as context generally leads to worse performance compared to using class labels, especially when the number of timesteps is increased. This finding supports the claim that optimizing the ELBO is not invariant to complex forward processes, and that choosing an appropriate diffusion process significantly impacts performance.
This figure compares the properties of different noise schedules used in diffusion models. The left panel shows a table summarizing the properties of MULAN (the proposed method) and a typical scalar noise schedule. It highlights that MULAN is multivariate, learned, and adaptive, which are improvements over the standard scalar approach. The right panel shows a bar chart comparing the likelihood (measured in bits per dimension, or BPD) achieved by different diffusion models on the CIFAR-10 dataset without data augmentation. MULAN achieves the lowest BPD, indicating better performance in likelihood estimation.

The figure compares the properties of MULAN’s noise schedule to a typical scalar noise schedule. The left panel shows a table summarizing key properties: MULAN is multivariate, learned, and adaptive, resulting in improved ELBO (Evidence Lower Bound) estimates of the likelihood. The right panel shows that MULAN achieves state-of-the-art likelihood (measured in bits-per-dimension or BPD) on CIFAR-10 without data augmentation.

This figure compares the properties of MULAN and scalar noise schedules, highlighting MULAN’s improvements in likelihood estimation due to its multivariate and adaptive nature. The left panel presents a table summarizing the key properties of different noise schedules, showcasing MULAN’s unique features. The right panel shows the likelihood (BPD) achieved by various diffusion models on the CIFAR-10 dataset, demonstrating that MULAN obtains a new state-of-the-art.

The figure compares different noise schedule properties, highlighting the advantages of the proposed MULAN method over conventional scalar approaches. The left panel shows a table summarizing key properties of different noise schedules (MULAN, scalar, learned, adaptive), indicating whether each method is multivariate, learned, adaptive, and improves ELBO (Evidence Lower Bound). The right panel presents a bar chart visualizing the likelihood (in bits-per-dimension or BPD) achieved by various diffusion models on the CIFAR-10 dataset (without data augmentation). MULAN achieves the best likelihood.

This figure compares the properties of different noise schedules used in diffusion models. The left panel shows a table summarizing the key properties of MULAN (a multivariate, learned, and adaptive noise schedule) and scalar noise schedules. The right panel presents a bar chart showing the bits-per-dimension (BPD) achieved by various diffusion models (including MULAN) on the CIFAR-10 dataset. The results demonstrate the superior performance of MULAN in terms of likelihood estimation.

The figure compares MULAN and scalar noise schedules, highlighting MULAN’s advantages in improving likelihood due to its multivariate and adaptive nature. It also shows the BPD achieved by MULAN and other methods on CIFAR-10.

The figure compares the properties of different noise schedules used in diffusion models. The left panel shows a table summarizing the key properties of MULAN (a learned, multivariate, and adaptive noise schedule) and typical scalar noise schedules. The right panel displays a bar chart comparing likelihoods (in bits-per-dimension, or BPD) achieved by several diffusion models on CIFAR-10 dataset. MULAN achieves a state-of-the-art likelihood, highlighting the advantages of its adaptive noise schedule.

This figure compares the properties of MULAN’s noise schedule with a typical scalar noise schedule. The left panel shows a table summarizing key differences between the two approaches highlighting MULAN’s multivariate and adaptive nature, which lead to better likelihood. The right panel shows the likelihood (BPD) achieved by various models on CIFAR-10, demonstrating MULAN’s state-of-the-art performance.
This figure compares different noise schedules. The left panel shows a table summarizing the properties of different noise schedules, highlighting the advantages of MULAN (multivariate, learned, and adaptive) in improving the ELBO (evidence lower bound). The right panel presents a bar chart showing the likelihood (measured in bits per dimension or BPD) achieved by various methods on the CIFAR-10 dataset without data augmentation. MULAN achieves the lowest BPD (2.55), indicating superior performance in likelihood estimation.
More on tables
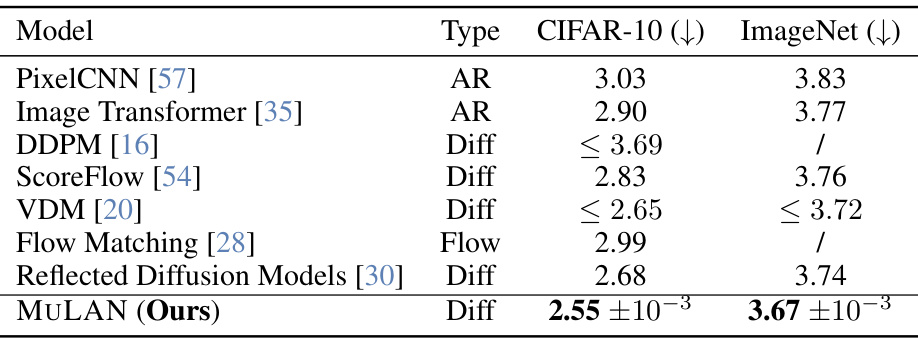
This table compares the likelihood (in bits per dimension or BPD) achieved by various generative models on the CIFAR-10 and ImageNet datasets. The models are categorized into autoregressive (AR), normalizing flow (Flow), and diffusion (Diff) models. The results shown are for the test sets and only include results from experiments performed without data augmentation. A slash (’/’) indicates that the original paper did not report the BPD for that specific dataset and model.
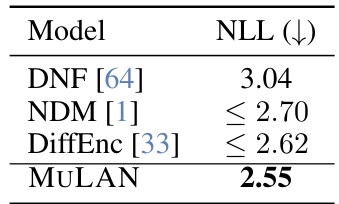
This table compares the negative log-likelihood (NLL) performance of MULAN against other state-of-the-art learned diffusion models on the CIFAR-10 dataset. It demonstrates that MULAN achieves a significantly lower NLL, indicating better density estimation compared to Diffusion Normalizing Flows (DNF), Neural Diffusion Models (NDM), and DiffEnc.

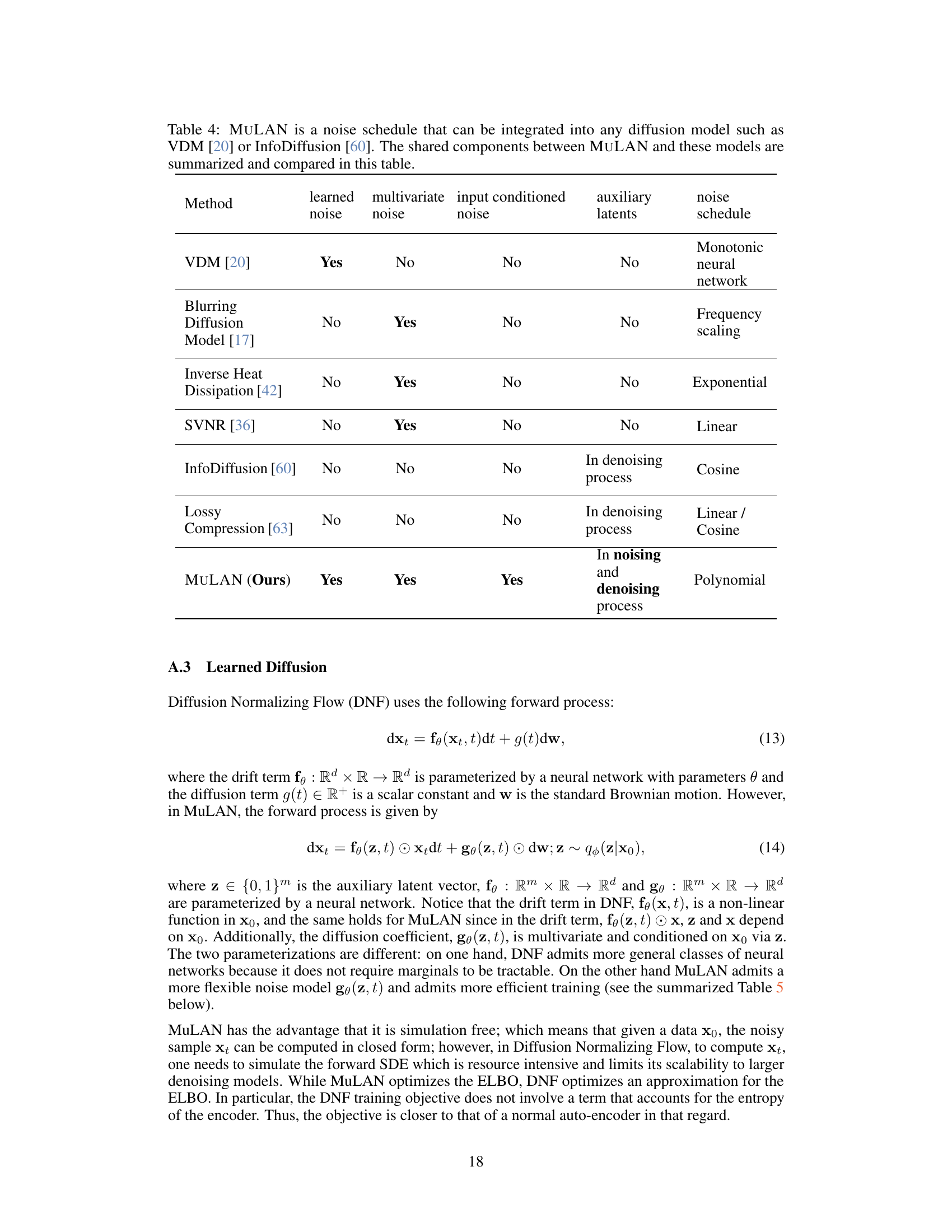
This table compares MULAN with other related methods that use custom noise schedules. It highlights key differences in terms of whether the noise process is learned, whether it is multivariate, whether it is input-conditioned, whether auxiliary latent variables are used, and the type of noise schedule employed. The table helps to demonstrate MULAN’s novelty and its improvements compared to prior work.
This table compares the negative log-likelihood (NLL) performance of MULAN against three other learned diffusion methods on the CIFAR-10 dataset. It highlights MULAN’s superior performance in terms of achieving a lower negative log-likelihood, indicating better density estimation compared to its competitors.
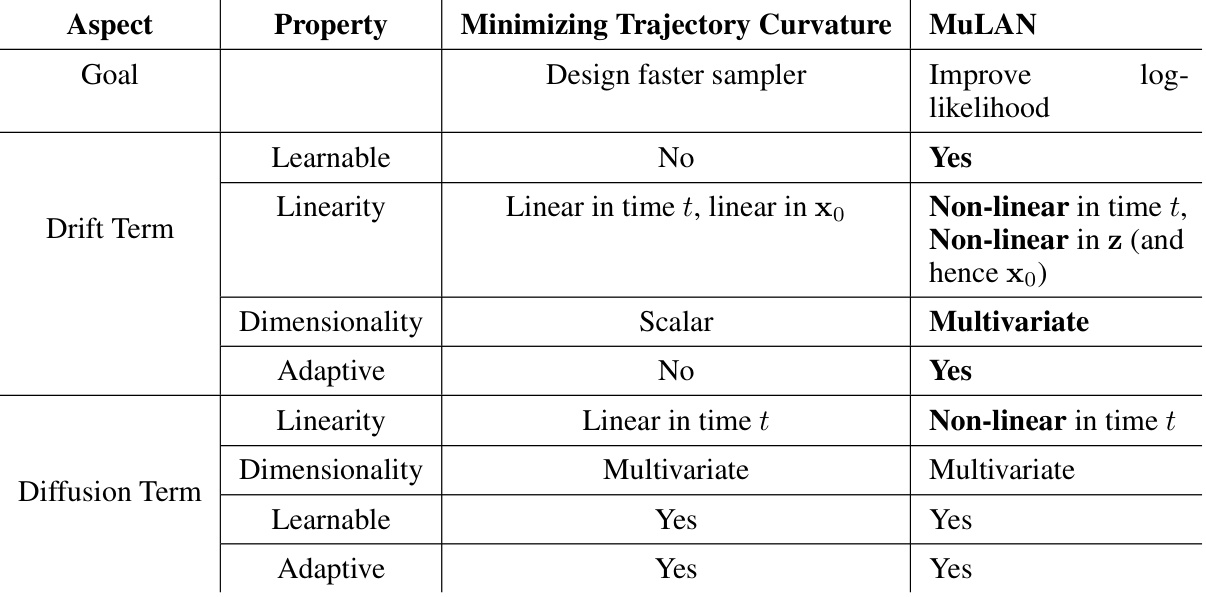
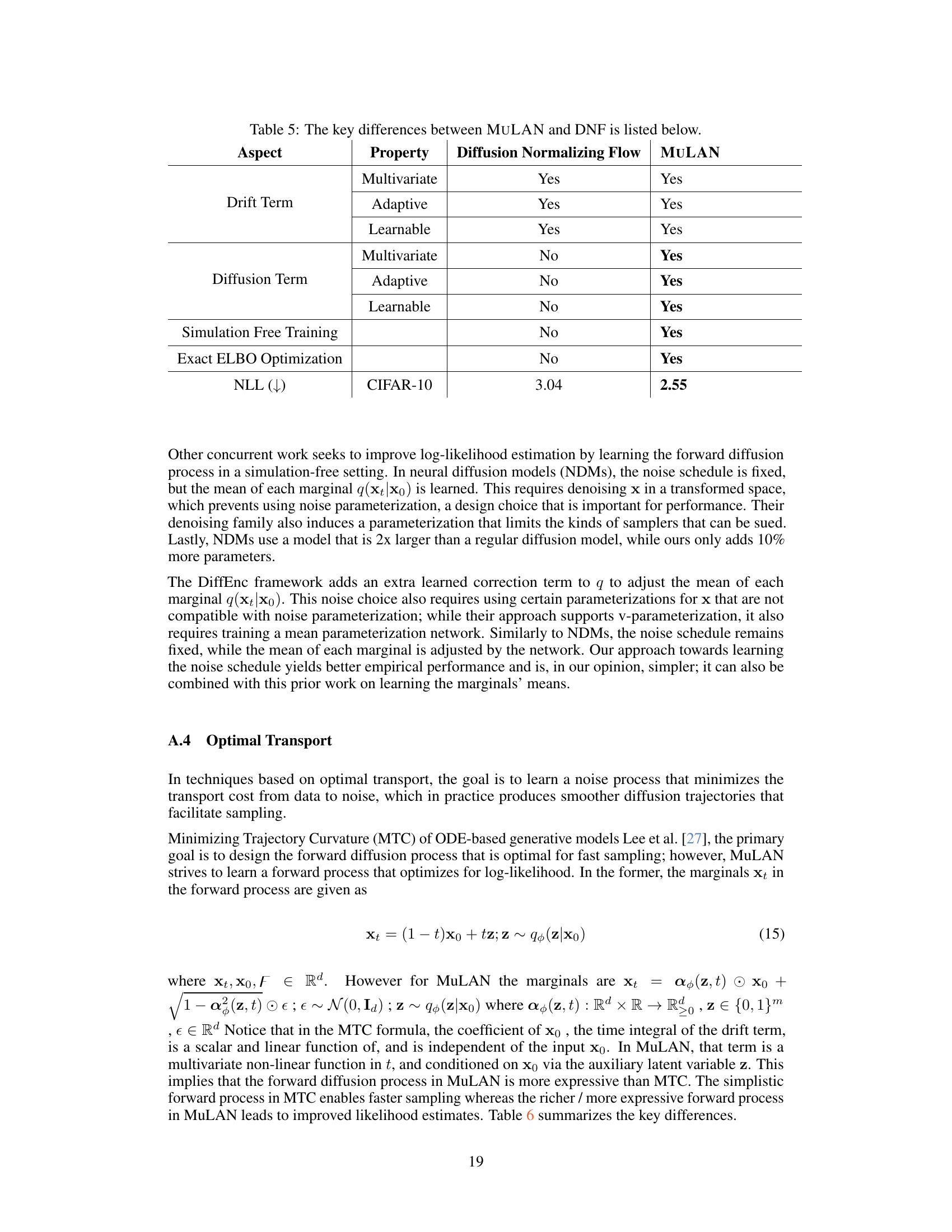
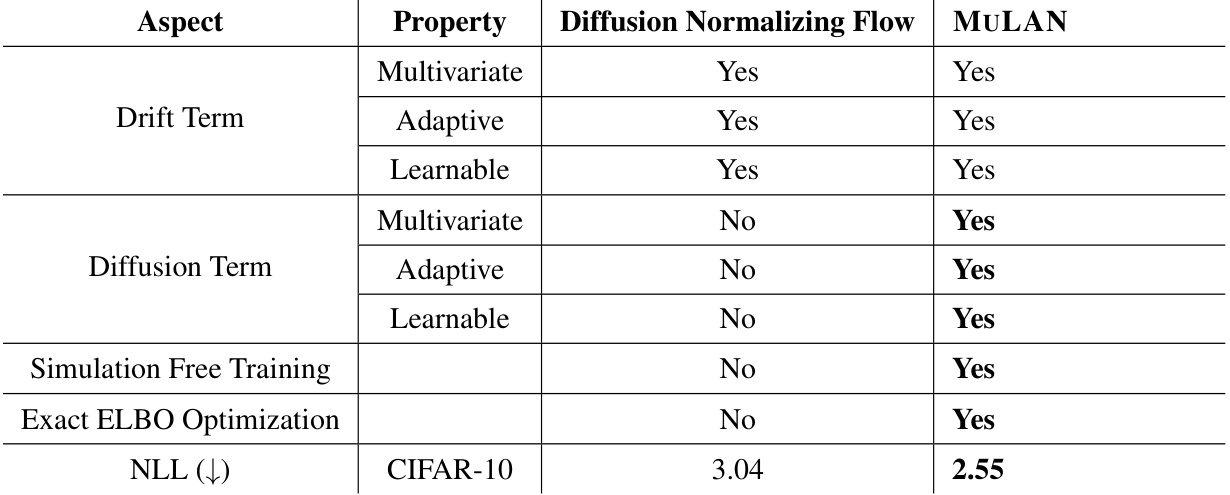
This table compares the key properties of the forward diffusion processes used in MULAN and Diffusion Normalizing Flow (DNF). It highlights differences in the drift and diffusion terms, specifically noting whether these components are multivariate, adaptive, and learnable. The table also points out that MULAN uses exact ELBO optimization, unlike DNF, and shows that MULAN achieves a superior negative log-likelihood (NLL) score on the CIFAR-10 dataset.
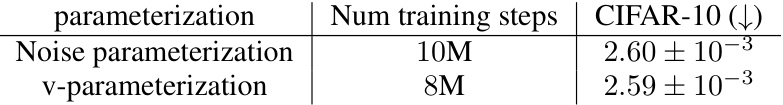
This table presents the test set likelihood in bits per dimension (BPD) on CIFAR-10 dataset. The results are computed using the Variational Lower Bound (VLB) estimation method. The table compares two parameterizations of the noise process in the MULAN model, namely, noise parameterization and v-parameterization, with different training steps. The mean and 95% confidence interval of the BPD values are reported for each parameterization and training step configuration.

This table compares the performance of the vanilla VDM model and the VDM model enhanced with MULAN on the CIFAR-10 dataset. It presents the VLB estimate (a lower bound on the likelihood), FID score (a measure of sample quality), and the number of function evaluations (NFE) required. The results are shown for different numbers of training steps and highlight the improvement in likelihood and sample quality achieved by MULAN, even with significantly fewer training steps.
Full paper#