Neglected Hessian component explains mysteries in sharpness regularization

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on sharpness regularization and second-order optimization in deep learning. It challenges existing assumptions by highlighting the significance of the often-neglected Nonlinear Modeling Error (NME) component of the Hessian. The findings provide valuable insights for designing better activation functions, interpreting the behavior of gradient penalties and weight noise, and developing improved regularization techniques. This work directly addresses current limitations in understanding sharpness, offers new avenues for research into activation function design and optimizers, and has direct implications for improving the generalization of deep learning models.

Visual Insights

#

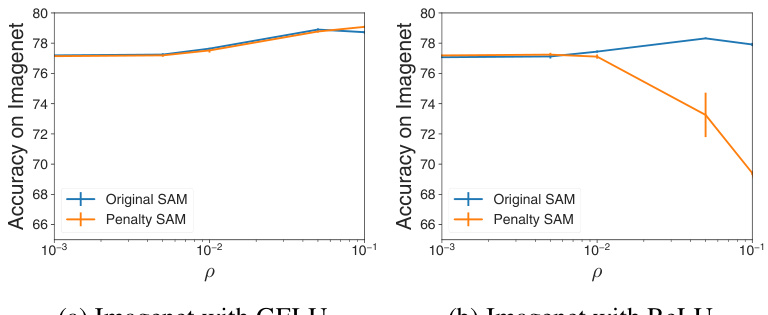
This figure compares the test accuracy of the original SAM algorithm and Penalty SAM (PSAM) across different datasets and activation functions (GELU and ReLU). The x-axis represents the hyperparameter ρ, which controls the perturbation size in SAM. The y-axis shows the test accuracy. The figure demonstrates that PSAM with GELU activation functions behaves similarly to the original SAM algorithm, whereas PSAM with ReLU shows a significant performance degradation at larger values of ρ.

In-depth insights

#

Hessian’s Hidden Role

#

The concept of “Hessian’s Hidden Role” in a research paper likely centers on the often-overlooked contributions of the Hessian matrix’s less prominent components in machine learning optimization. While the Gauss-Newton approximation of the Hessian is frequently used due to its positive semi-definite nature, ignoring the Nonlinear Modeling Error (NME) matrix can lead to inaccurate conclusions. The NME, with its indefinite nature and sensitivity to activation function properties, can significantly impact generalization performance and algorithm stability. Understanding the NME’s influence on gradient penalties and weight noise regularization is crucial, as its role in these techniques is usually disregarded. The paper likely reveals how the NME impacts regularization effectiveness, explaining inconsistencies between seemingly similar methods like sharpness-aware minimization and gradient penalties. It is important to investigate whether the NME’s contribution is beneficial or detrimental depending on the specific algorithm and learning context. In essence, the paper emphasizes the necessity of a more complete Hessian analysis that incorporates the NME, leading to improved algorithm design and a deeper understanding of model optimization.

Activation Effects

#

The analysis of activation functions’ effects on the performance of sharpness regularization reveals crucial insights into the behavior of gradient penalties. The NME (Nonlinear Modeling Error) component of the Hessian is particularly sensitive to the choice of activation function, specifically its second derivative. Activation functions like ReLU, with poorly defined or numerically unstable second derivatives, hinder the effectiveness of gradient penalties, whereas functions like GELU, possessing smooth and numerically stable derivatives, exhibit improved performance. This sensitivity highlights the importance of the NME in second-order regularization, which is often overlooked. Understanding the NME’s intricate relationship with activation functions is critical for designing effective sharpness regularization methods. Moreover, it suggests the need for thoughtful activation function selection or modification to ensure compatibility with methods using second order information in training neural networks.

Penalty Pitfalls

#

The section on “Penalty Pitfalls” would likely explore the challenges and limitations of using gradient penalty methods for regularization in neural networks. A key insight would be the sensitivity of gradient penalties to the choice of activation function, particularly highlighting the impact of the second derivative of the activation function on the performance. The analysis would likely demonstrate how activation functions like ReLU, with their discontinuous derivatives, lead to poor performance, while smoother functions like GELU yield better results. The core issue is linked to the Hessian’s structure: gradient penalties implicitly rely on the nonlinear modeling error (NME) component of the Hessian, and this component is highly sensitive to the second derivative of the activation function. The analysis would delve into the mathematical relationship between gradient penalties, SAM, and the NME, demonstrating the conditions under which gradient penalties approximate SAM and the situations where they fail. Finally, the section would probably propose potential solutions or mitigations, possibly including strategies to modify or replace activation functions to improve gradient penalty performance and design interventions to handle poorly behaved second derivatives.

NME’s Importance

#

The research highlights the often-overlooked Nonlinear Modeling Error (NME) matrix, a component of the Hessian matrix in deep learning models. The NME’s significance lies in its encoding of second-order information related to the model’s features, unlike the Gauss-Newton matrix which primarily reflects second-order information about the loss function itself. This distinction is crucial because the NME’s properties influence the effectiveness of sharpness regularization techniques. The paper demonstrates empirically that the NME’s sensitivity to activation function derivatives explains the varied success of methods like gradient penalties, which fail to generalize well when NME-related numerical issues arise. Conversely, the NME plays a crucial role in methods like weight noise, and simply minimizing it proves detrimental. The study advocates for considering the NME in both theoretical analysis and experimental design for a more comprehensive understanding of sharpness regularization in deep learning, ultimately leading to more robust and generalizable models.

Future Directions

#

Future research could explore the impact of activation function choice on the NME’s contribution to sharpness regularization, designing activation functions specifically optimized for compatibility with second-order methods. Investigating how different optimizers interact with the NME, including those that implicitly incorporate second-order information, is crucial. Further exploration of the relationship between NME and generalization is needed beyond trace-based measures, exploring a wider array of geometric quantities and activation functions. Developing new sharpness regularization techniques that directly incorporate and leverage the NME could significantly advance the field. Finally, extending the analysis to more complex network architectures such as transformers and exploring the interplay between the NME and inherent inductive biases of these models would be highly valuable.

More visual insights

#

More on figures

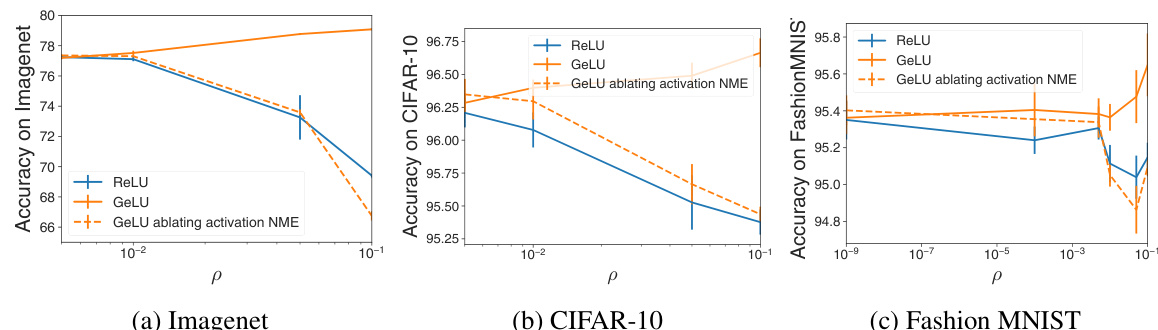
This figure shows the test accuracy as the hyperparameter p increases for three different datasets (Imagenet, CIFAR-10, and Fashion MNIST). Three different activation functions are used: ReLU, GELU, and GELU with the activation NME ablated. The results demonstrate that removing information from the NME reduces the effectiveness of the gradient penalty, particularly for ReLU and GELU with ablated NME. This supports the paper’s claim that the NME is crucial for understanding the performance of gradient penalty regularization.

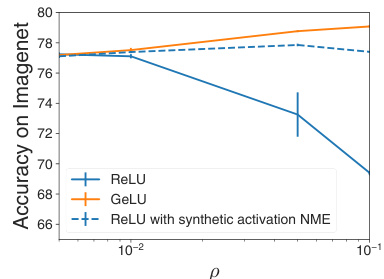
This figure shows the test accuracy on the ImageNet dataset as the hyperparameter p increases for different activation functions. The experiment involves adding synthetic information to the Nonlinear Modeling Error (NME) component of the Hessian, specifically for the ReLU activation function. The results indicate that adding synthetic NME improves the performance of the gradient penalty regularization method as p gets larger. The control groups using ReLU and GeLU without synthetic NME are shown for comparison.

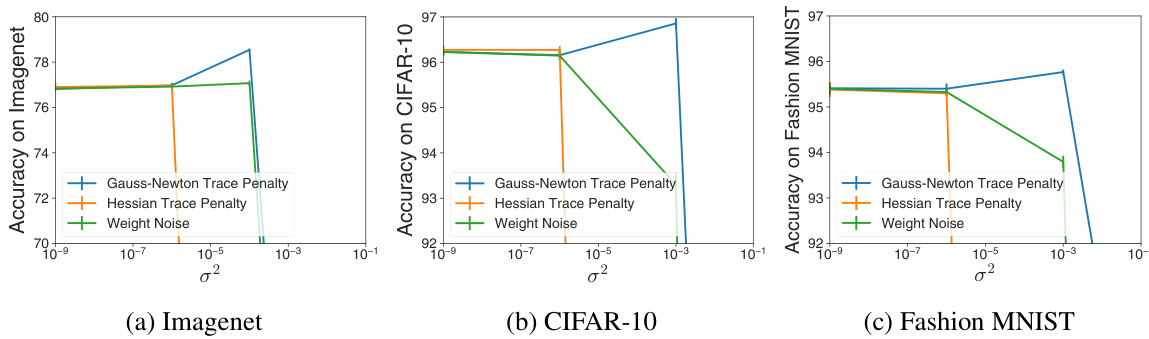
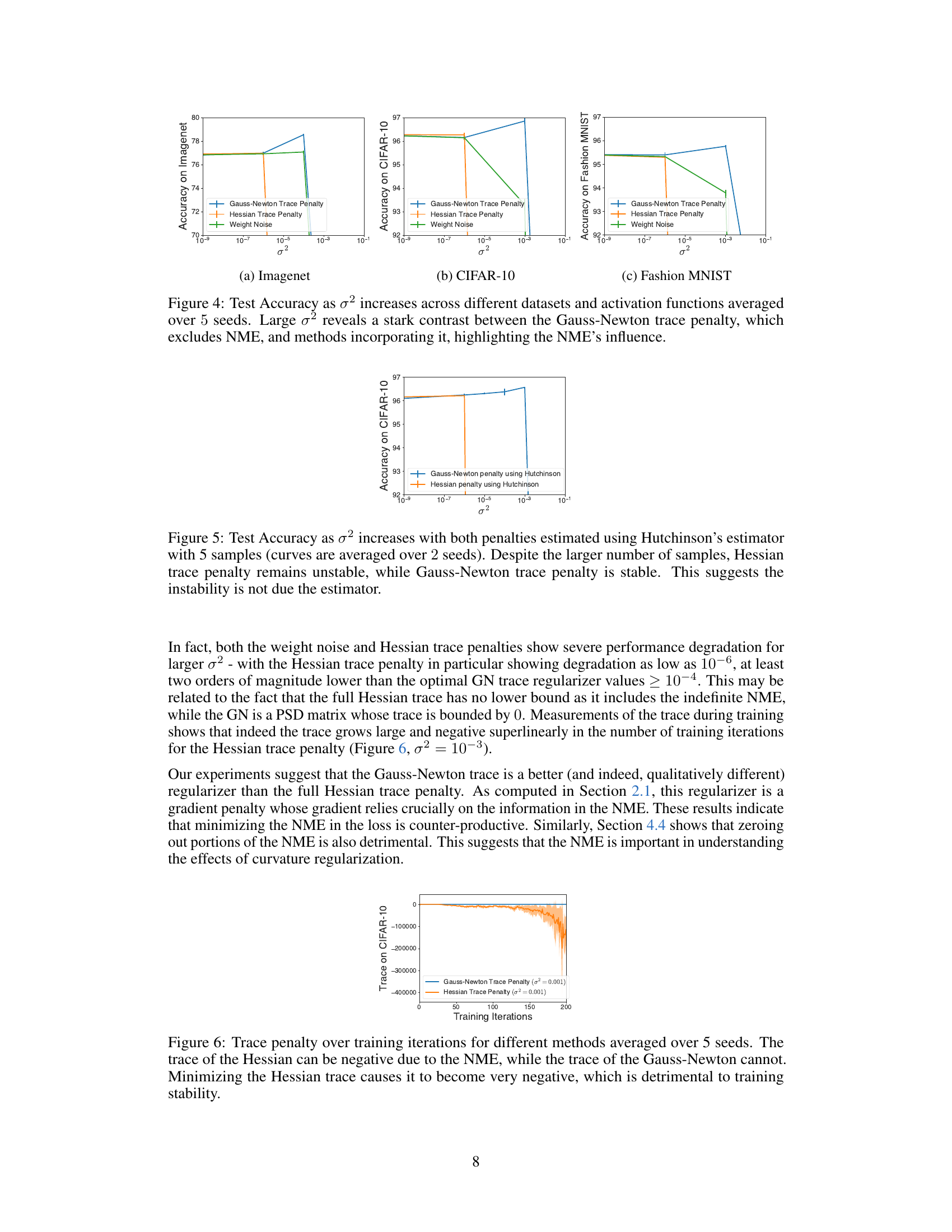
This figure compares the test accuracy of three different methods (Gauss-Newton Trace Penalty, Hessian Trace Penalty, and Weight Noise) across three datasets (Imagenet, CIFAR-10, and Fashion MNIST) as the hyperparameter σ² increases. The Gauss-Newton Trace Penalty, which ignores the Nonlinear Modeling Error (NME) component of the Hessian, shows consistently better performance than the Hessian Trace Penalty and Weight Noise, both of which include the NME. This highlights the detrimental effect of minimizing the NME during training and the importance of considering the NME in sharpness regularization.

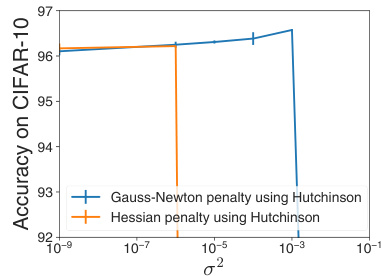
The figure compares the test accuracy of two different penalty methods (Gauss-Newton and Hessian trace penalty) against the noise parameter (σ²) in weight noise experiments. The Gauss-Newton penalty shows stable and consistent performance across various noise levels. In contrast, the Hessian penalty shows significantly unstable performance, exhibiting large fluctuations in accuracy. Despite increasing the number of samples used in the Hutchinson estimator (from one in Figure 4 to five here), the instability of the Hessian penalty persists. This suggests that the instability is not solely due to the limitations of the estimation method, but rather inherent in the nature of the Hessian penalty itself.

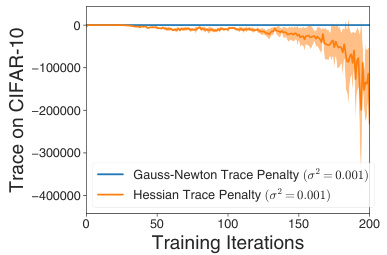
This figure shows the trace of the Hessian and Gauss-Newton matrices over training iterations for two different methods: Hessian Trace Penalty and Gauss-Newton Trace Penalty. The key takeaway is that minimizing the Hessian trace, which includes the Nonlinear Modeling Error (NME), leads to increasingly negative values and instability. In contrast, the Gauss-Newton trace remains stable and close to zero. This illustrates the detrimental impact of minimizing the NME during training.

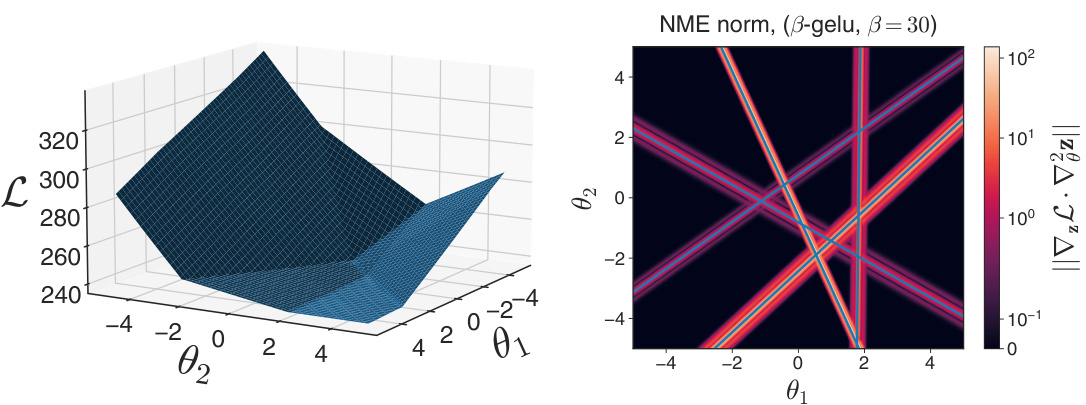
The figure shows the loss landscape and the norm of the Nonlinear Modeling Error (NME) for a two-parameter model with ReLU and β-GELU activations. The left panel shows that the ReLU activation results in a piecewise quadratic loss landscape, whereas β-GELU produces a smoother surface. The right panel visualizes the NME, illustrating how it highlights the boundaries between different linear regions in the ReLU case, providing information about the model’s ability to switch between these regions, whereas the β-GELU NME is largely concentrated near these boundaries.

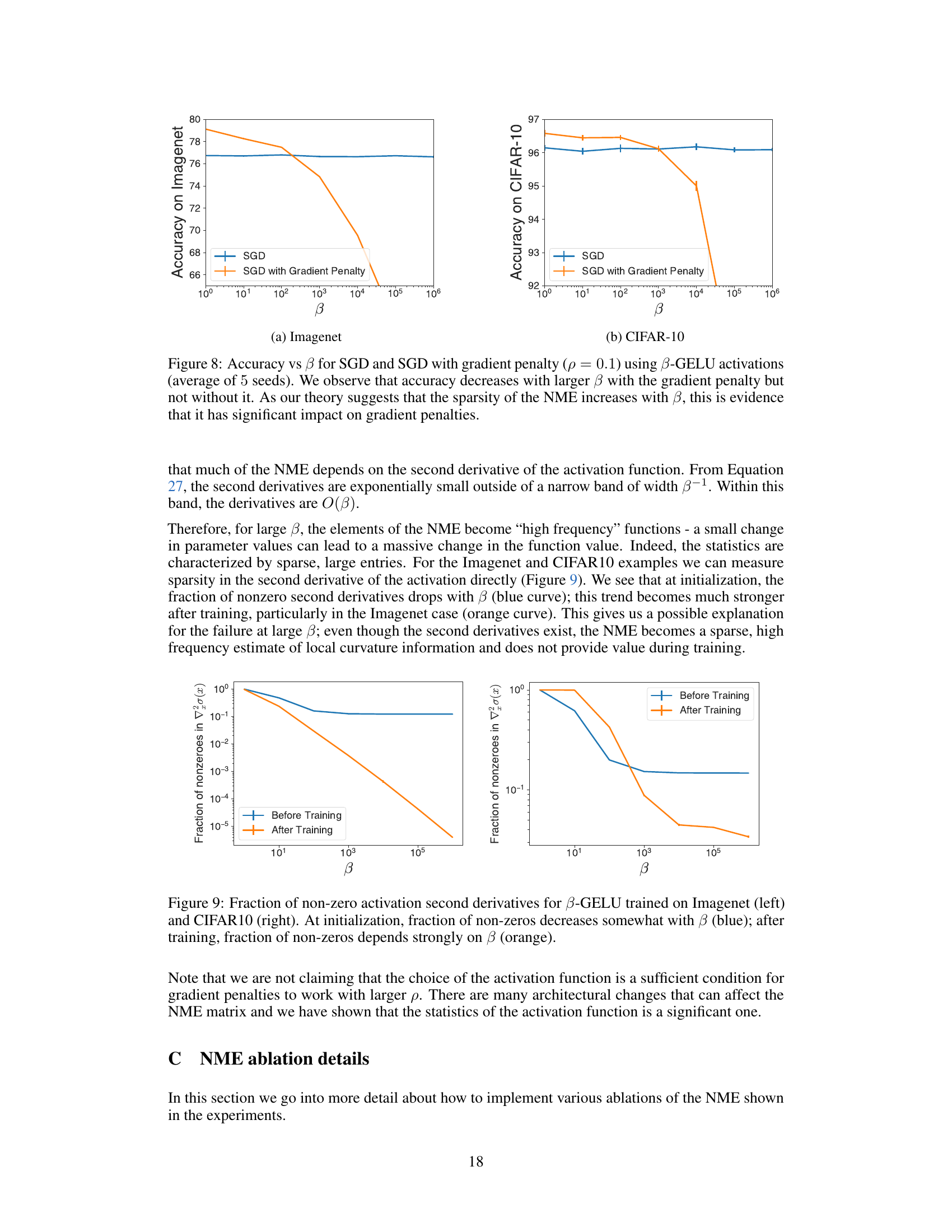
This figure compares the test accuracy of models trained using standard SGD and SGD with a gradient penalty, as the parameter β in the β-GELU activation function is varied. The results are shown for both the Imagenet and CIFAR-10 datasets. As β increases, the β-GELU activation function approaches the ReLU function. The figure shows that the gradient penalty significantly improves accuracy for smaller β, but as β increases and approaches ReLU, the benefit of the gradient penalty diminishes and even becomes detrimental, highlighting the importance of the NME (Nonlinear Modeling Error) component of the Hessian. The Gauss-Newton trace penalty, which excludes the NME, shows more stable performance across the range of β values.

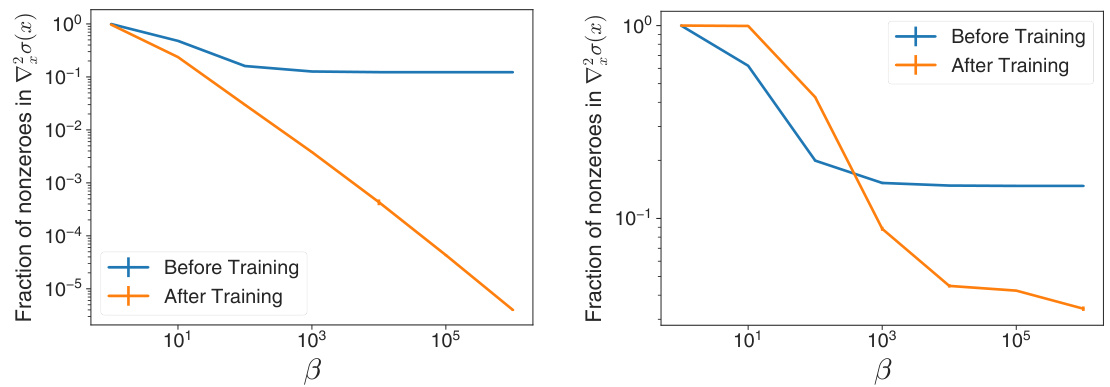
The figure shows the fraction of non-zero second derivatives of the β-GELU activation function before and after training on the ImageNet and CIFAR-10 datasets. It illustrates how the sparsity of the second derivative changes with the β parameter, especially after training. The high sparsity for large β values contributes to the failure of gradient penalties with ReLU-like activations.

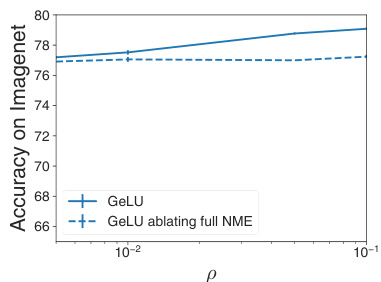
This figure shows the impact of ablating the full Nonlinear Modeling Error (NME) from the gradient penalty update rule on the test accuracy. The experiment uses GELU activation functions. Two lines are shown: one for the standard GELU activation, and one for GELU with the NME component removed from its gradient penalty calculations. The results demonstrate that removing the NME significantly reduces performance across all values of the hyperparameter p.

Full paper

#