↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Scene flow estimation, crucial for autonomous systems, struggles with real-world noise and occlusion. Existing methods often lack reliability measures. This creates a significant challenge, as inaccurate estimations can have serious consequences in safety-critical applications.
DiffSF tackles this issue by ingeniously integrating transformer-based scene flow estimation with denoising diffusion models. This approach not only improves accuracy and robustness, but also provides uncertainty estimates through multiple hypotheses generation. The results demonstrate significant improvements over the state-of-the-art on various benchmarks, confirming the effectiveness of the approach in handling noisy data and occlusions. The uncertainty estimates further enhance the reliability of predictions, making DiffSF a highly promising solution for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is important because it presents DiffSF, a novel approach to scene flow estimation that significantly improves accuracy and robustness while also providing uncertainty estimates. This addresses a critical need in real-world applications and opens new avenues for research in uncertainty quantification and robust model design. The integration of diffusion models enhances the reliability and trustworthiness of scene flow predictions, making it highly relevant to autonomous driving, robotics, and other safety-critical applications.
Visual Insights#

This figure illustrates the diffusion process used in the DiffSF model. The forward diffusion process starts with the ground truth scene flow (Vo) and iteratively adds Gaussian noise until a completely noisy state (VT) is reached. The reverse process, used during training and inference, learns to reconstruct the original scene flow (Vo) from the noisy state (VT), conditioned on the source and target point clouds. This process allows the model to handle noisy data and estimate uncertainty.

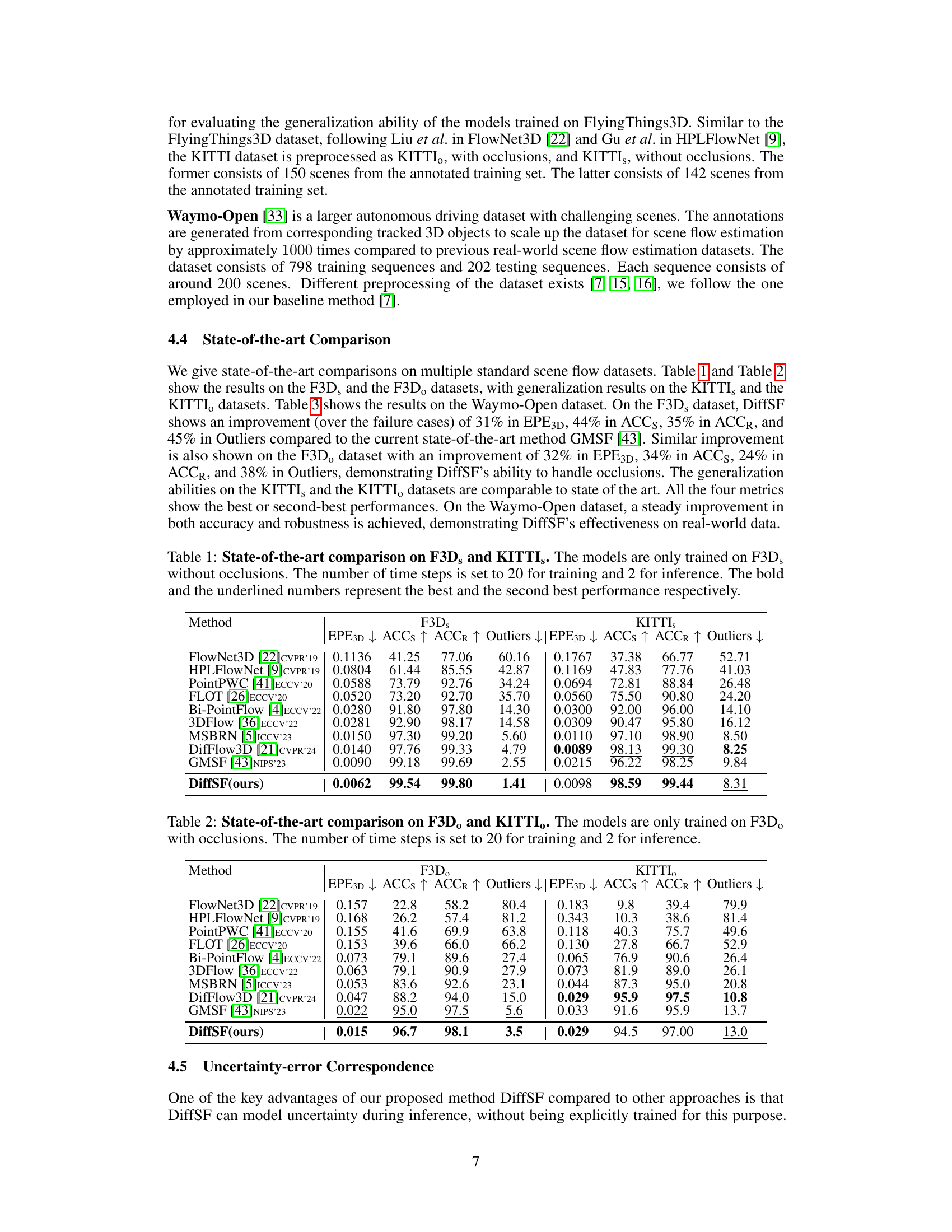
This table compares the proposed DiffSF model’s performance against other state-of-the-art methods on the F3Ds and KITTIs datasets. The models were trained only on the F3Ds dataset (without occlusions) and evaluated using four metrics: EPE3D, ACCs, ACCR, and Outliers. The number of diffusion time steps used for training and inference is specified. Bold and underlined values indicate the best and second-best performance, respectively. This demonstrates the model’s accuracy and robustness, especially considering that it wasn’t trained on the KITTIs dataset.
In-depth insights#
DiffSF: Scene Flow#
DiffSF, a novel scene flow estimation method, leverages denoising diffusion probabilistic models to enhance accuracy and robustness. By framing scene flow estimation as a diffusion process, DiffSF addresses challenges posed by noisy inputs and occlusions in real-world data, surpassing previous state-of-the-art methods. The diffusion process’s inherent noise filtering capability improves robustness, while the introduction of randomness provides a measure of uncertainty in predictions. This is a significant advantage, particularly in safety-critical applications. Furthermore, DiffSF employs a transformer-based architecture, which significantly improves the model’s ability to capture complex relationships in the data. The combination of diffusion models and transformers offers a unique and powerful approach to scene flow estimation, opening up exciting opportunities for future research. The experimental results, including the uncertainty-error correspondence, further validate DiffSF’s efficacy and contribute to the field’s progress in handling real-world scenarios.
Diffusion Model Use#
This research leverages diffusion models in a novel way for scene flow estimation. Instead of using them for generation, the core idea is to frame scene flow prediction as a reverse diffusion process. This approach starts with noisy data representing the scene flow and progressively refines it to obtain an accurate and robust estimation. The beauty of this method lies in its ability to handle noisy inputs and occlusions inherently, which are common challenges in real-world applications. By sampling multiple times with varied initial states, the model provides uncertainty estimates along with the predictions, thus enhancing its reliability for downstream safety-critical tasks. This addresses a crucial limitation of many existing methods which output solely deterministic scene flow estimations without associated confidence levels. The combination of diffusion models with transformer-based architectures represents a significant advancement, allowing for the learning of complex relationships between source and target point clouds for precise and uncertainty-aware scene flow prediction.
Uncertainty Modeling#
This research paper explores uncertainty modeling within the context of scene flow estimation, a challenging computer vision task. The core idea revolves around leveraging the inherent stochasticity of diffusion models to quantify and incorporate uncertainty directly into the scene flow prediction process. Unlike traditional methods that primarily focus on point estimates, this approach generates multiple hypotheses by sampling from the diffusion model’s posterior distribution. This results in robustness to noisy inputs and occlusions, a significant improvement over existing approaches. The uncertainty estimates are not an afterthought; they are intrinsically linked to the prediction process, providing valuable information about the confidence of the model’s output. Importantly, experimental results demonstrate a strong correlation between predicted uncertainty and the actual prediction error, showcasing the practical utility of this approach for safety-critical applications. This innovative method offers a crucial step towards more reliable and trustworthy scene flow estimation, particularly relevant in domains where accurate uncertainty quantification is essential.
Robustness to Noise#
The concept of ‘Robustness to Noise’ in the context of scene flow estimation is crucial, as real-world data is inherently noisy due to sensor limitations and environmental factors. A robust model should effectively filter out irrelevant noise while accurately capturing the underlying scene flow. The paper likely addresses this by showcasing how the chosen approach, possibly leveraging denoising diffusion probabilistic models (DDPMs), mitigates the impact of noisy inputs. The diffusion process, by progressively adding and removing Gaussian noise, implicitly learns to distinguish between signal and noise. This characteristic is vital for enhancing accuracy in challenging conditions. Moreover, the ability to sample multiple hypotheses through the DDPM framework provides a mechanism for assessing prediction uncertainty. This uncertainty measure is not only valuable for identifying potentially unreliable predictions but can also improve the overall system’s robustness. Higher uncertainty often correlates with higher prediction error, thereby allowing the model to flag uncertain regions for potential refinement or alternative processing strategies. Ultimately, demonstrating strong performance on benchmarks with noisy datasets strongly supports the claim of enhanced robustness to noise.
Future Improvements#
Future improvements for scene flow estimation using diffusion models could focus on several key areas. Addressing limitations in handling highly dynamic scenes and severe occlusions remains crucial, potentially through incorporating more advanced motion models or exploring alternative diffusion architectures better suited for noisy or incomplete data. Improving efficiency is another major aspect; current diffusion models can be computationally expensive, hindering real-time applications. Investigating more efficient diffusion processes or hardware acceleration techniques is therefore vital. Enhancing uncertainty quantification is also key. While the presented method provides uncertainty estimates, further refinement is needed to ensure reliability and better calibration of uncertainty across various scenarios. Finally, extending the approach to more complex data modalities like incorporating color or semantic information would significantly increase the robustness and applicability of the system in real-world settings. Research into these areas would significantly advance the field of scene flow estimation.
More visual insights#
More on figures
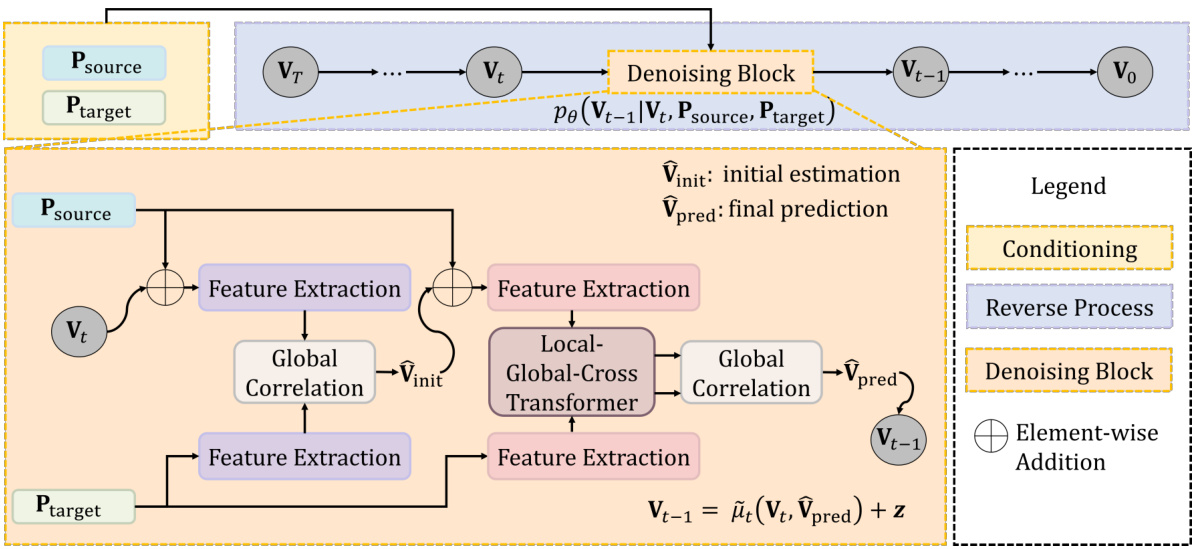
This figure shows the detailed architecture of the denoising block used in the reverse diffusion process for scene flow estimation. It illustrates how the noisy input (Vt), source point cloud (Psource), and target point cloud (Ptarget) are processed to produce the final scene flow prediction (Vpred). The process involves feature extraction, global correlation, and local-global-cross transformers to refine the prediction iteratively. The use of shared weights for feature extraction is also highlighted.

This figure analyzes the uncertainty estimation of the proposed method. The left panel shows the correlation between the endpoint error (EPE) and the estimated uncertainty, demonstrating an almost linear relationship, indicating that higher uncertainty values correspond to higher errors. The right panel presents a precision-recall curve for outlier prediction (EPE > 0.30 meters), showing the effectiveness of uncertainty as a measure for identifying outliers.

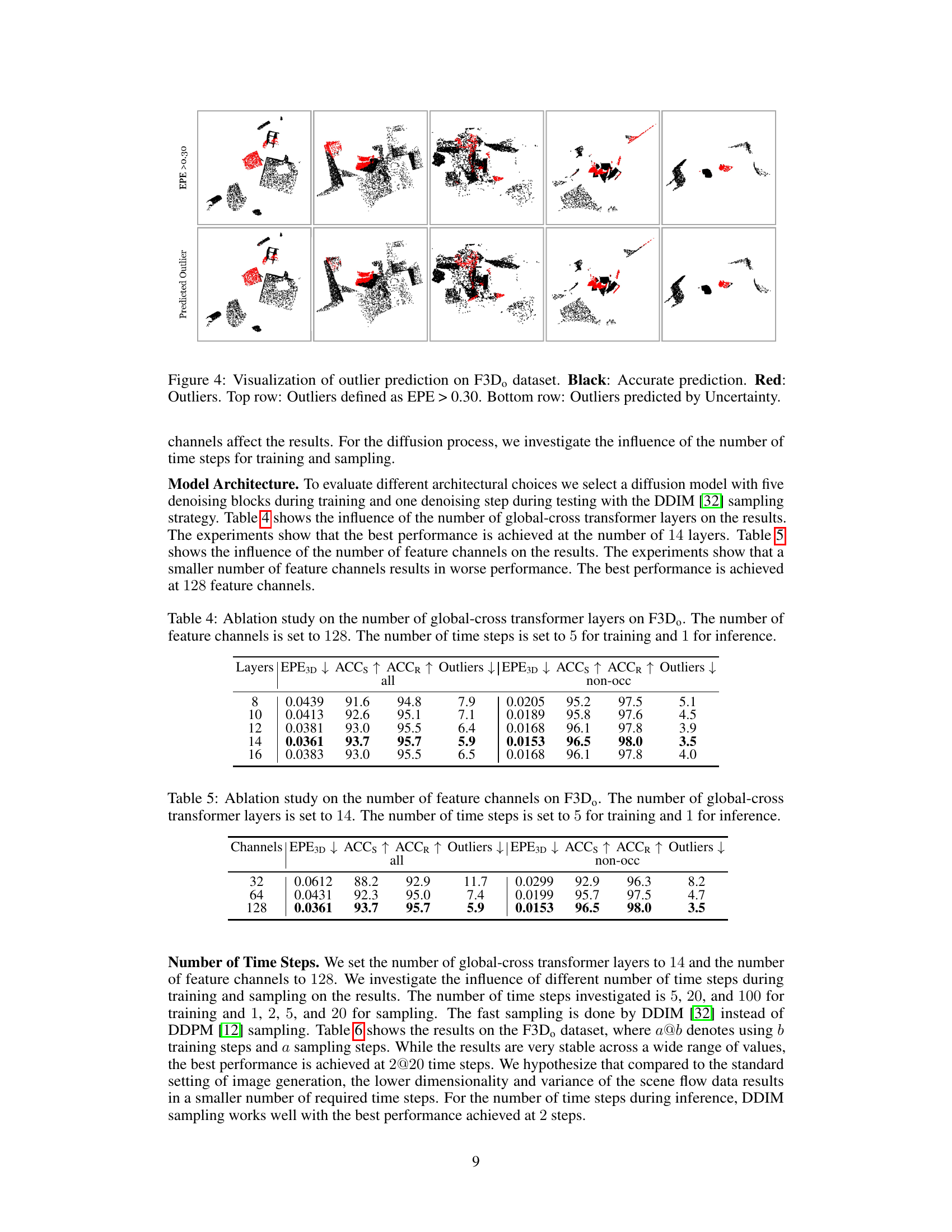
This figure visualizes the outlier prediction results on the F3D dataset. The top row shows the actual outliers, identified as having an Endpoint Error (EPE) greater than 0.30. The bottom row displays the outliers predicted by the model’s uncertainty estimation. Black points represent accurate predictions, while red points indicate outliers. The comparison between the two rows demonstrates the model’s capability to identify inaccurate predictions based on its estimated uncertainty.
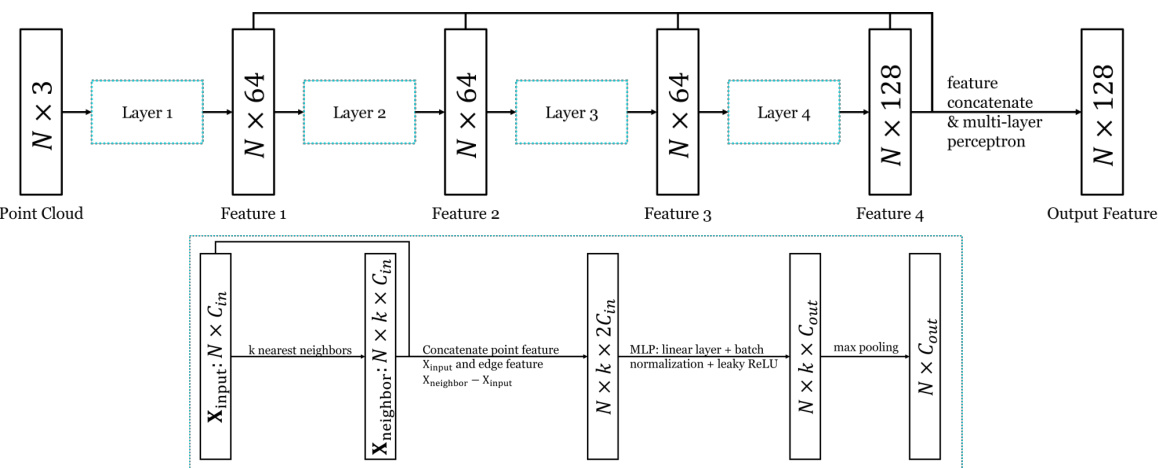
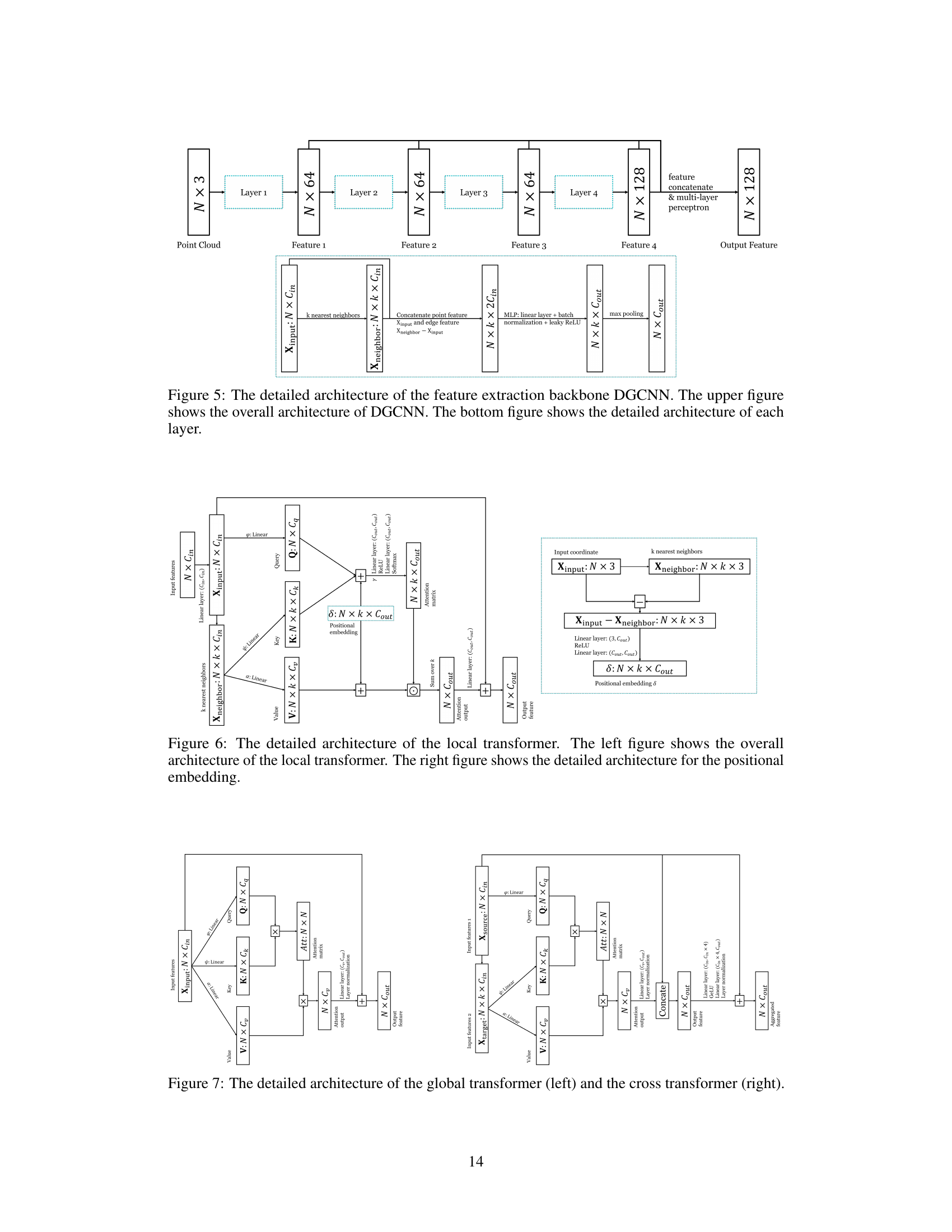
This figure shows the detailed architecture of the feature extraction backbone DGCNN used in the DiffSF model. The upper part illustrates the overall structure, showing how four layers of processing (Layer 1 to Layer 4) are connected sequentially. Each layer increases the feature dimension from the input point cloud, eventually culminating in an output feature with a dimension of 128. The lower part shows the inner workings of a single layer, detailing how the k-nearest neighbors of each point are identified, feature concatenation, multi-layer perceptron (MLP) application, and max pooling are performed to achieve the final features.

This figure shows the detailed architecture of the local transformer used in the DiffSF model for scene flow estimation. The left side illustrates the overall process, showing how the input features are processed through linear layers to generate queries, keys, and values for an attention mechanism. The keys and values are derived from k-nearest-neighbors of the input points. Positional embeddings are incorporated to improve the model’s ability to handle spatial relationships. The right side provides a detailed breakdown of how these positional embeddings are calculated, using a multi-layer perceptron (MLP) on the input coordinates and their k-nearest neighbors.

This figure illustrates the architecture of the denoising block used in the reverse diffusion process of DiffSF. The denoising block takes as input the noisy scene flow vector (Vt), the source point cloud (Psource), and the target point cloud (Ptarget). It processes these inputs through several components: Feature Extraction (to extract higher-dimensional features), Local-Global-Cross Transformer (to capture local, global, and cross-point relationships), and Global Correlation (to generate an initial scene flow estimation). Finally, a Denoising Block refines the initial estimation and outputs the denoised scene flow prediction (Vpred). The color-coding highlights the shared weights used within the Feature Extraction blocks.

This figure visualizes the denoising process of the diffusion model on the KITTI dataset. It shows four different steps in the reverse diffusion process, where the model iteratively refines its prediction of the scene flow starting from pure noise. Orange points represent the source point cloud warped according to the current prediction. Green points represent the target point cloud. The progression shows how the model gradually recovers the accurate scene flow from noise, indicating the denoising capability of the diffusion model.

This figure compares the performance of GMSF and DiffSF on the FlyingThings3D dataset by visualizing the warped source point clouds. Points are colored based on their endpoint error (EPE3D): green for low error and orange for high error. Blue points represent the target point cloud.

This figure compares the performance of GMSF and DiffSF on the FlyingThings3D dataset by visualizing the warped source points. Blue points represent the target point cloud, green points represent accurately warped source points (low EPE3D), and orange points represent inaccurately warped points (high EPE3D). It highlights the improved accuracy of DiffSF in handling challenging cases.
More on tables
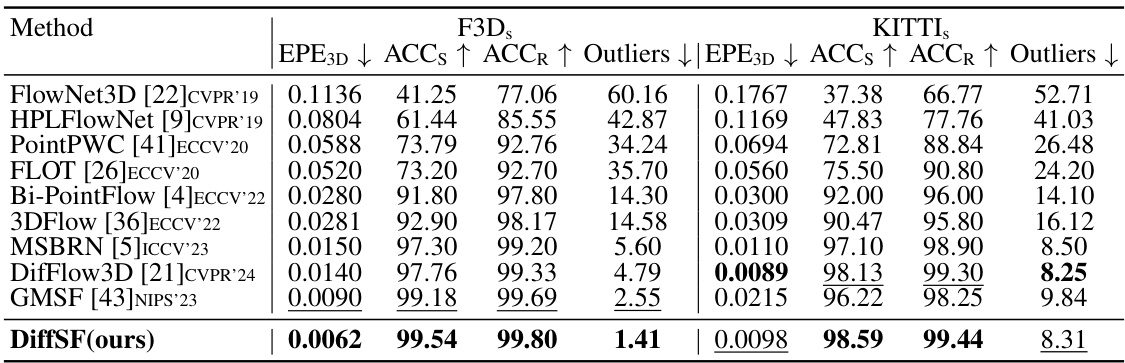
This table compares the proposed DiffSF model to other state-of-the-art scene flow estimation methods on the FlyingThings3D (F3Dₛ) and KITTI (KITTIs) datasets. The models were trained only on the F3Dₛ dataset (without occlusions), making it a generalization test on the KITTI dataset. The metrics used are Endpoint Error (EPE3D), Accuracy within 5cm (ACCS), Accuracy within 10cm (ACCR), and the percentage of outliers. The number of diffusion time steps used during training and inference are specified.
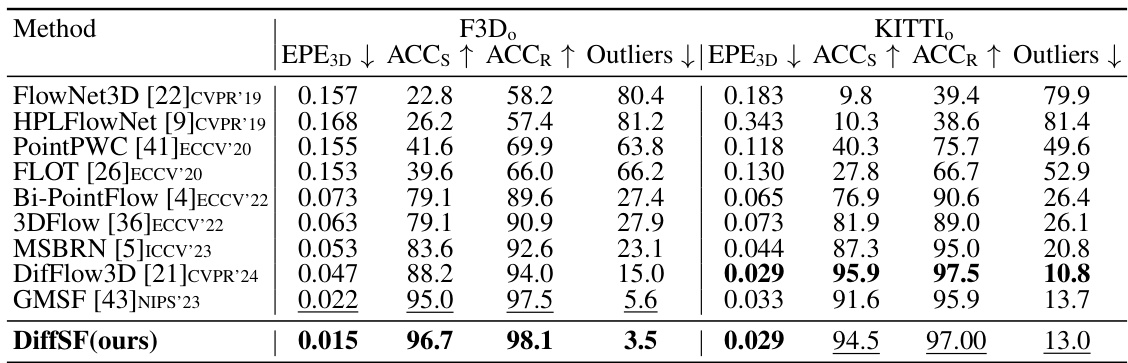
This table compares the performance of DiffSF against other state-of-the-art methods on the F3D dataset with occlusions and KITTI dataset. The metrics used are End Point Error 3D (EPE3D), Accuracy within 5cm (ACCs), Accuracy within 10cm (ACCR), and Outliers. It highlights DiffSF’s performance when trained only on data with occlusions and its generalization ability on the KITTI dataset.
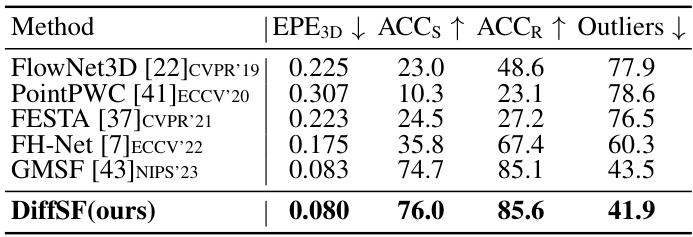
This table compares the performance of DiffSF against other state-of-the-art methods on the Waymo-Open dataset. It shows that DiffSF achieves better performance in terms of EPE3D, ACCs, ACCR, and Outliers, demonstrating its effectiveness in handling challenging real-world scenarios.

This table presents the ablation study on the number of global-cross transformer layers used in the model. The study was conducted on the F3D dataset with 128 feature channels and 5 training steps, 1 inference step. The results (EPE3D, ACCs, ACCR, Outliers) are shown for both the complete dataset and the non-occluded subset. The table shows how different numbers of layers (8, 10, 12, 14, 16) affect the model’s performance.

This table presents the ablation study on the number of feature channels used in the model’s architecture for scene flow estimation on the F3D dataset. The results show how the model’s performance (EPE3D, ACCs, ACCR, and Outliers) varies with different numbers of feature channels (32, 64, and 128) while keeping the number of global-cross transformer layers and time steps constant. It aims to determine the optimal number of feature channels for achieving the best performance.
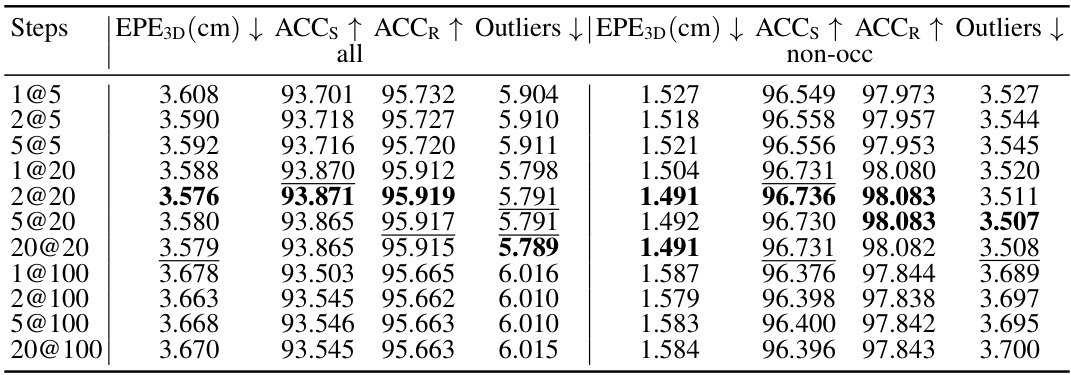
This table presents a comparison of the proposed DiffSF model against state-of-the-art methods on two scene flow datasets: F3Dₛ (FlyingThings3D without occlusions) and KITTIₛ (KITTI without occlusions). The models were trained only on the F3Dₛ dataset. The evaluation metrics used are EPE3D (Endpoint Error), ACCs (percentage of points with an endpoint error smaller than 5cm or relative error less than 5%), ACCr (percentage of points with an endpoint error smaller than 10cm or relative error less than 10%), and Outliers (percentage of points with an endpoint error larger than 30cm or relative error larger than 10%). The number of diffusion steps used during training was 20 and during inference was 2. Bold values indicate the best performance, while underlined values indicate second-best.

This table presents an ablation study comparing the performance of the proposed DiffSF method against the baseline GMSF method on the F3D dataset. It analyzes the impact of incorporating improved architecture and the diffusion process on the overall performance, showing improvement in accuracy and robustness metrics when both improvements are included.
Full paper#