Diffusion Priors for Variational Likelihood Estimation and Image Denoising

OuKW8cUiuY

Jun Cheng et el.

TL;DR
#

Real-world image denoising is hampered by complex, signal-dependent noise, which current methods struggle to model accurately. Existing diffusion-based approaches either simplify noise types or rely on approximate posterior estimation, limiting effectiveness. This restricts their use in scenarios with structured or signal-dependent noise.

This paper introduces a novel approach that uses adaptive likelihood estimation and maximum a posteriori (MAP) inference during reverse diffusion. By combining a non-identically distributed likelihood with noise precision, it dynamically infers precision posterior using variational Bayes and refines the likelihood. A local Gaussian convolution further rectifies estimated noise variance, leading to improved denoising. The use of low-resolution diffusion models directly handles high-resolution images, enhancing efficiency. Experiments show that this method outperforms existing techniques on various real-world datasets.

Key Takeaways
#

Why does it matter?
#

This paper is important because it offers a novel approach to real-world image denoising, a crucial task in computer vision. By integrating adaptive likelihood estimation and MAP inference within the reverse diffusion process, it surpasses existing methods in handling complex, signal-dependent noise. Its data efficiency and applicability to high-resolution images make it particularly relevant for real-world applications where data acquisition is expensive or limited. The exploration of local diffusion priors from low-resolution models opens up new avenues for efficient processing of high-resolution imagery.

Visual Insights
#

This figure shows the results of generating high-resolution (HR) images from low-resolution (LR) diffusion models. The left side displays 256x256 images sampled from a 128x128 diffusion model, highlighting the local nature of the generated textures. The right side shows 512x512 images sampled from a 256x256 diffusion model, further emphasizing this locality. This demonstrates that the pre-trained LR diffusion model can be used to directly handle high-resolution noisy images by leveraging the inherent local diffusion prior.

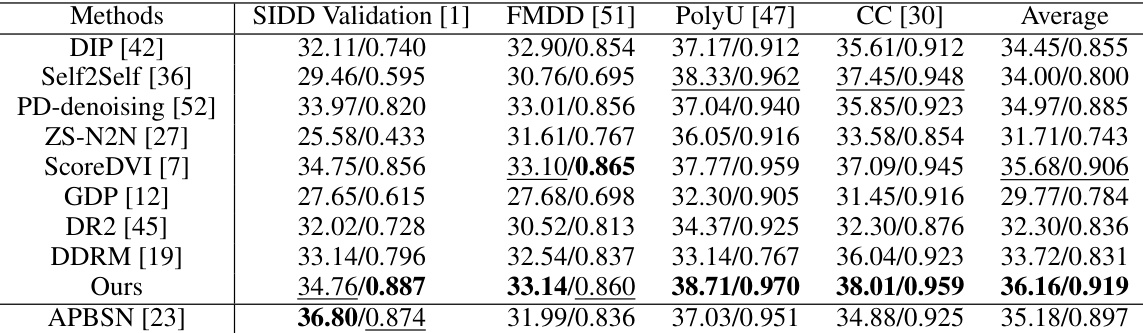
This table presents a quantitative comparison of different image denoising methods on four real-world datasets (SIDD, FMDD, PolyU, CC). The comparison uses two metrics: Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM). The best and second-best results for each dataset are highlighted in bold and underlined respectively, allowing for easy identification of top-performing methods.

In-depth insights
#

Diffusion Priors
#

Diffusion models, known for their exceptional generative capabilities, have recently emerged as powerful priors for image restoration tasks. Leveraging diffusion priors involves integrating the degraded image into the generation process of a pre-trained diffusion model, effectively guiding the model towards a clean reconstruction. This approach offers several advantages over traditional methods: it avoids the need for large paired datasets and can handle complex, real-world noise patterns more effectively. However, challenges remain. Many existing methods based on diffusion priors oversimplify the noise model (e.g., assuming simple Gaussian noise), limiting their applicability to complex real-world scenarios. Others rely on approximate posterior inference, potentially sacrificing accuracy for computational efficiency. Future research should focus on improving the accuracy of likelihood modeling, handling structured and signal-dependent noise, and developing more efficient inference techniques. The integration of variational Bayes offers a promising avenue for addressing the limitations of approximate inference, allowing for adaptive likelihood estimation and more accurate posterior inference during the reverse diffusion process. This, combined with clever techniques such as employing local diffusion priors from low-resolution models, represents a significant advancement in real-world image denoising.

Variational Bayes
#

Variational Bayes (VB) is a crucial technique in Bayesian inference, particularly useful when dealing with intractable posterior distributions. Its core idea is to approximate a complex, true posterior distribution with a simpler, tractable variational distribution. This approximation is optimized by minimizing the Kullback-Leibler (KL) divergence between the true and variational posteriors. In the context of the research paper, VB likely plays a vital role in estimating the precision (inverse variance) of the noise model. This is particularly challenging in real-world image denoising due to the complex, non-independent nature of noise. By using VB, the algorithm can effectively approximate the posterior distribution of the precision parameter without resorting to computationally expensive methods. The dynamic inference of this precision throughout the reverse diffusion process allows the algorithm to adapt to the spatial variability of real-world noise, increasing its robustness. The choice of a tractable variational distribution (e.g., Gamma distribution for precision) is also critical for the computational efficiency and scalability of VB within the overall framework.

MAP Inference
#

Maximum a Posteriori (MAP) inference is a crucial Bayesian method for estimating the most probable value of a parameter given observed data. In the context of image denoising, MAP inference aims to find the clean image that maximizes the posterior probability, considering both the likelihood of observing the noisy image given the clean image and the prior probability of the clean image itself. This prior encodes assumptions about the nature of clean images, often leveraging learned representations from deep generative models. The effectiveness of MAP inference hinges on accurately modeling the noise, which can be complex and signal-dependent in real-world scenarios. Furthermore, efficient inference algorithms are essential, especially when dealing with high-dimensional image data. The challenges often involve balancing the fidelity to the noisy observation with the regularization provided by the prior. Variational methods can provide tractable approximations to complex posterior distributions, enabling more efficient MAP estimation in these challenging situations.

Real-world Noise
#

Real-world noise in image data presents a significant challenge for computer vision tasks. Unlike idealized Gaussian noise, real-world noise is complex, exhibiting characteristics such as signal dependency and spatial correlation. This means the noise level and patterns often change depending on the underlying image content, and noise in adjacent pixels is not independent. Standard denoising techniques often struggle with such intricate noise structures. Methods relying on assumptions of simple noise models may yield suboptimal results, failing to accurately capture the nuances of real-world image degradation. Effective denoising in real-world settings necessitates advanced modeling techniques that can adapt to the unique characteristics of each image and its associated noise. This might include incorporating statistical priors or using complex deep learning models that are capable of learning non-linear relationships between the image and the noise itself. Successfully addressing real-world noise is critical for improving the accuracy and robustness of various computer vision applications.

Local Diffusion
#

The concept of ‘Local Diffusion’ in the context of image restoration using diffusion models is a significant advancement. It leverages the observation that low-resolution (LR) diffusion models, when used to generate high-resolution (HR) images, exhibit a localized behavior. This means that the generated texture and details primarily focus on smaller regions rather than globally impacting the entire image. This localized effect serves as a powerful advantage in denoising HR images because it avoids the computational burden and potential information loss associated with patch-based or resizing techniques that are frequently employed with HR images and pre-trained LR models. This locality inherent in LR models can be seen as a form of implicit spatial regularization, simplifying the denoising process significantly and making it more efficient. By directly applying this LR diffusion prior to HR noisy images, the method bypasses the need for complex pre-processing steps and directly handles the high-resolution data. This approach is both efficient and preserves image details effectively, thus highlighting the potential of exploiting localized properties within diffusion models for improved image restoration.

More visual insights
#

More on figures

This figure shows a visual comparison of different denoising methods applied to images from the SIDD validation dataset. The results demonstrate the visual quality of denoising using several different methods. The denoised images are compared to the ground truth (GT) images to illustrate the performance of each method. It is a visual representation of the quantitative results reported in Table 2 of the paper.

This figure compares the visual results of different denoising methods on the SIDD validation dataset. It shows a section of a noisy image alongside the results obtained by several methods: DIP, Self2Self, PD-denoising, ZS-N2N, ScoreDVI, GDP, DR2, DDRM, APBSN, and the proposed method. The comparison allows for a visual assessment of the effectiveness of each method in removing noise while preserving image details and textures. The ground truth (GT) image is also included for reference.

This figure consists of two subfigures. Subfigure (a) shows visual results of the estimated noise variance β₀/α₀. The brighter the color is, the larger the value of β₀/α₀ will be, representing higher noise variance. Subfigure (b) shows the relationship between PSNR and the average β₀/α₀ over the entire SIDD dataset. It demonstrates an inverse correlation; images with higher average β₀/α₀ tend to have lower PSNR values.

This figure shows a visual comparison of different denoising methods applied to images from the SIDD validation dataset. It provides a qualitative assessment of the results by visually comparing the denoised images produced by different methods against the ground truth. This allows for a direct visual comparison of the effectiveness of different techniques in removing noise from real-world images.

This figure shows a visual comparison of different denoising methods applied to a real-world image from the PolyU dataset. The image depicts a close-up of some electronic components and wires. It highlights the differences in denoising performance across various methods, including the proposed approach, showing improvements in noise reduction and detail preservation. The comparison visually demonstrates that the proposed approach performs superior denoising while preserving image details.

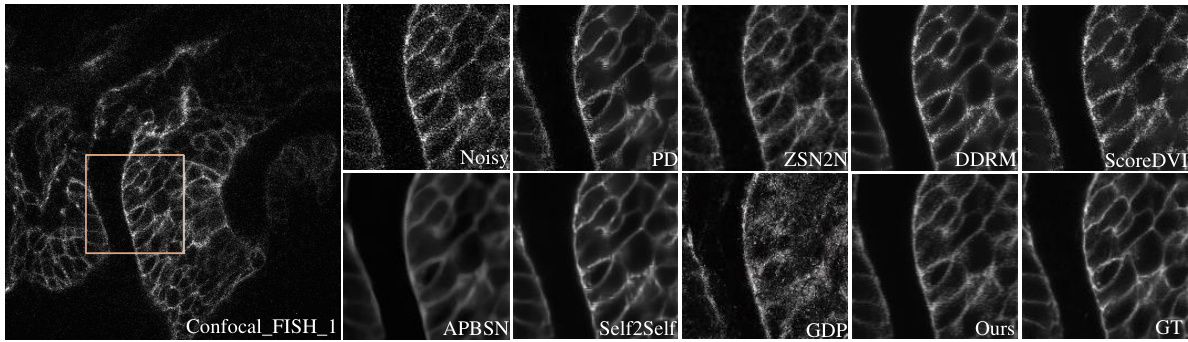
This figure shows the visual comparison of different denoising methods on the FMDD dataset. The methods compared include Noisy (original noisy image), PD, ZS-N2N, DDRM, ScoreDVI, APBSN, Self2Self, GDP, Ours (the proposed method), and GT (ground truth). The zoomed-in section highlights the differences in detail preservation and noise removal between the methods. The figure demonstrates the superior performance of the proposed method in restoring fine details and reducing noise effectively compared to other existing methods.

This figure compares different image denoising methods on the PolyU dataset, showing visual results and PSNR/SSIM values for each method. The methods compared include: PD-denoising, APBSN, DR2, Self2Self, ZS-N2N, GDP, DDRM, ScoreDVI, and the proposed method. The figure highlights the visual quality differences between methods and shows that the proposed method achieves the highest PSNR/SSIM scores.

This figure compares the denoising results of different methods on Bernoulli noise with p=0.2. It shows two example images and their denoised versions using ZS-N2N and the proposed method, along with the ground truth. The figure visually demonstrates the effectiveness of the proposed method in reducing noise while preserving image details and textures, especially compared to ZS-N2N which leaves noticeable artifacts.