↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Transformer-based models often struggle with handling structural information in data due to the inherent permutation invariance of dot-product attention. Existing positional encoding techniques are often ad-hoc and lack theoretical grounding, hindering their generalizability and interpretability. This paper addresses these limitations by introducing a new framework called Algebraic Positional Encodings (APE). APE leverages group theory to map algebraic specifications of different data structures (sequences, trees, grids) to orthogonal operators, preserving the algebraic characteristics of the source domain.
The APE method is shown to significantly improve performance across various tasks, including sequence transduction, tree transduction, and image recognition. Unlike existing methods, APE achieves this without task-specific hyperparameter optimization, showcasing its adaptability and robustness. The results demonstrate that APE’s group theoretic foundation leads to more interpretable and generalizable models, providing insights into the role of structural biases in Transformer architectures. The code for APE is also publicly available.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with Transformers because it introduces a novel positional encoding strategy that significantly improves model performance across various tasks and data structures. It addresses the limitations of existing ad-hoc methods by providing a flexible, theoretically grounded framework, opening avenues for improved model interpretability and generalizability. Its focus on group theory offers a new perspective on positional encoding, valuable for advancing research in various areas.
Visual Insights#
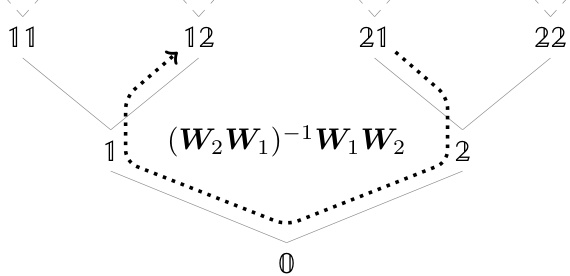
This figure visualizes example paths and their corresponding interpretations (matrix multiplications) for sequences, trees, and grids. It illustrates how the algebraic positional encoding (APE) method maps paths to matrix operations, highlighting the relative positions between tokens in each structure.
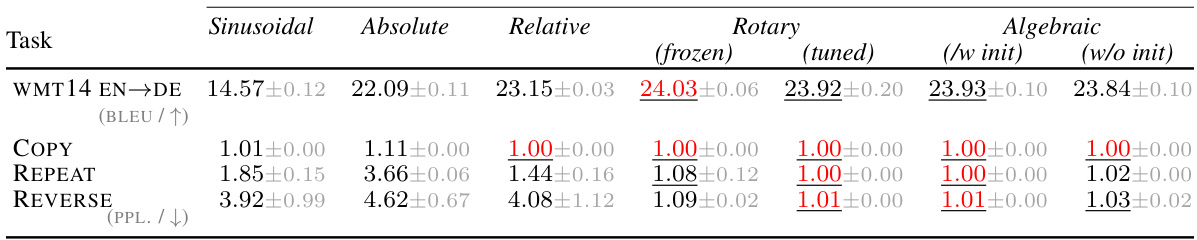
This table presents a comparison of the performance of different positional encoding schemes across various tasks, including machine translation, synthetic sequence transduction, tree transduction, and image recognition. It shows the BLEU score for machine translation, perplexity scores (PPL) for sequence tasks, and accuracy scores for image recognition. The results are broken down by positional encoding method (Sinusoidal, Absolute, Relative, Rotary, Algebraic) and, in some cases, further by initialization method (with or without initialization) and trainability of parameters (frozen or tuned). The table highlights the best performing method for each task and indicates when the confidence intervals overlap with the top performer. The results demonstrate that algebraic positional encodings consistently outperform or match the state-of-the-art, even without hyperparameter optimization.
In-depth insights#
APE: Positional Encoding#
Algebraic Positional Encodings (APE) offer a novel approach to positional encoding in Transformer-style models, addressing limitations of existing methods. APE leverages group theory to map algebraic structures (sequences, grids, trees) into orthogonal operators, preserving structural properties and avoiding ad-hoc designs. This theoretically grounded approach allows for a unified framework applicable across diverse data types. Empirical results demonstrate performance comparable to or exceeding state-of-the-art methods, without hyperparameter tuning, highlighting the efficiency and generalizability of APE. The connection to Rotary Positional Embeddings (ROPE) is established, showing APE as a more flexible and theoretically sound generalization. Overall, APE provides a strong foundation for future advancements in positional encoding, promoting both interpretability and performance in various neural network architectures.
Algebraic Framework#
An algebraic framework for positional encoding offers a rigorous and generalizable approach to handling positional information in transformer-style models. Unlike ad-hoc methods, it leverages group theory to represent various data structures (sequences, trees, grids) algebraically. This allows for the consistent application of the encoding across different data types, preserving structural properties. By interpreting these structures as subgroups of orthogonal operators, the framework produces attention-compatible vector operations. This approach is theoretically grounded, leading to a better understanding of the encoding’s behavior and facilitating the design of novel and improved positional encoding methods. The key advantage lies in the framework’s ability to move beyond empirical approaches and provide a unified foundation for positional encodings, opening up avenues for future exploration and innovation in this field.
Group Theory Lens#
A ‘Group Theory Lens’ applied to positional encoding in Transformer models offers a powerful framework for understanding and designing these encodings. By viewing positional information through the lens of group theory, the inherent structure and relationships within various data types (sequences, trees, grids) become explicit. This approach moves beyond ad-hoc methods, enabling a more principled and generalizable construction of positional encodings. The algebraic properties of groups provide a robust mathematical foundation, ensuring that the resulting encodings maintain desirable structural characteristics. This allows for a more systematic and less empirically driven approach compared to traditional techniques. The homomorphism between syntactic specifications of data structures and their semantic interpretation as orthogonal operators is particularly insightful. This ensures that the model’s behavior faithfully reflects the underlying data structure. This framework is not just theoretically elegant; it also produces highly effective positional encodings, showing competitive or superior performance on various tasks, suggesting its practical utility. The unification and generalization across different data types—from sequences to trees and grids—are significant advantages, suggesting that this framework could simplify and streamline the development of domain-specific Transformer models.
Empirical Evaluation#
An empirical evaluation section in a research paper should thoroughly investigate the proposed method’s performance. It needs to clearly define the metrics used to assess performance, detail the experimental setup, including datasets, training parameters, and comparison methods. The results should be presented transparently, often with statistical significance tests to support claims of improvement. Robustness analysis is crucial, exploring sensitivity to parameter changes and evaluating performance across various scenarios or datasets. A strong empirical evaluation should demonstrate not only the effectiveness of the proposed method but also its limitations and areas for future improvement. Careful consideration of baselines is needed for a fair comparison. The evaluation must be reproducible with sufficient details provided to allow others to replicate the experiments. Finally, the implications of the findings should be discussed in the context of the research problem and future research directions.
Future Extensions#
Future extensions of algebraic positional encodings (APE) could explore several promising avenues. Extending APE to handle more complex group structures beyond those already considered (sequences, trees, grids) is a key area. This might involve investigating how to represent and encode positions in graphs, manifolds, or other non-Euclidean spaces using group-theoretic tools. Incorporating inductive biases beyond structural properties is another important direction. For instance, the current framework could be enhanced to incorporate domain-specific knowledge or constraints, such as symmetries in physics or linguistic structures. Investigating the interplay between APE and different attention mechanisms is crucial. While the paper focuses on dot-product attention, exploring compatibility and potential benefits with other attention schemes (e.g., linear attention, sparse attention) could yield significant improvements. Finally, developing more efficient computational methods for large-scale applications is vital. The quadratic complexity of the current implementation could limit applicability to very large datasets. Exploring alternative matrix representations or approximation techniques could be key for scaling APE to real-world problems.
More visual insights#
More on tables
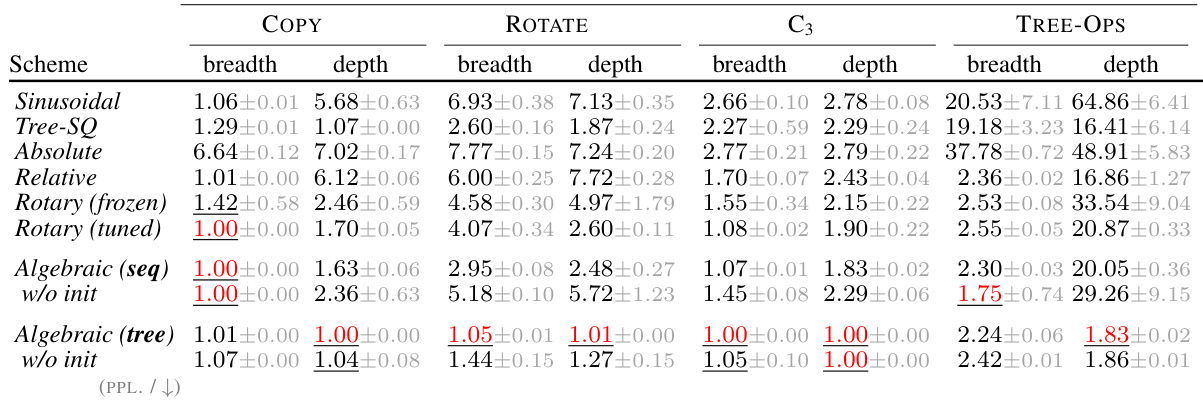
This table presents the quantitative results of the experiments conducted in the paper, comparing the performance of Algebraic Positional Encodings (APE) against several strong baselines across various tasks involving sequences, trees, and images. For each task and method, the table reports the performance metric (BLEU for machine translation and sequence transduction tasks, perplexity for algorithmic tree manipulation, and accuracy for image recognition). The results show APE achieving competitive or superior performance in most cases, highlighting its robustness and generalizability.
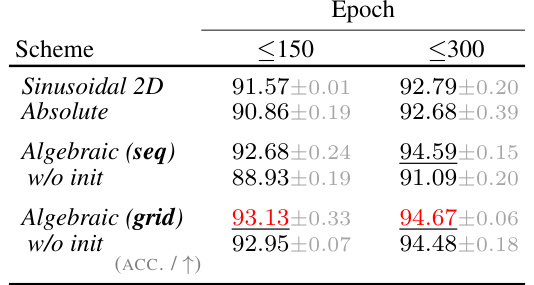
This table presents a comparison of the performance of different positional encoding methods across various tasks, including machine translation, synthetic sequence transduction, tree transduction, and image recognition. For each task, multiple metrics (BLEU score for machine translation, perplexity for synthetic tasks, and accuracy for image recognition) and methods (Sinusoidal, Absolute, Relative, Rotary, Algebraic with and without initialization) are shown, with their performance and confidence intervals. The best-performing model for each task is highlighted.

This table lists the hyperparameters used in the experiments described in the paper, broken down by experiment type (NMT, Transduction, Image). It shows the specific values used for parameters such as convolution size, embedding size, feedforward size (for encoder and decoder), activation function, number of layers and heads, normalization method, and the position of normalization (pre or post). These settings were chosen to enable a fair and comparable evaluation across the different tasks.
Full paper#



















