↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Training recurrent neural networks (RNNs) for neuroscience applications poses significant challenges due to ill-conditioned loss surfaces, limited GPU memory, and inherent sequential operations in many second-order optimization algorithms. These issues severely hinder the investigation of brain dynamics underlying complex tasks, especially those requiring long time horizons. Existing optimization methods like Adam often struggle with these issues, leading to slow convergence or failure to find a solution.
This research introduces SOFO, a novel second-order optimization method that addresses these limitations. SOFO leverages batched forward-mode differentiation, resulting in constant memory usage over time, unlike backpropagation. Its efficient use of GPU parallelism makes it faster than many other second-order optimizers, while achieving vastly superior performance than Adam in various RNN tasks, including double-reaching motor tasks and adaptive Kalman filter learning over long horizons. The results indicate that SOFO is a promising technique for tackling complex RNN training problems, facilitating progress in computational neuroscience and beyond.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computational neuroscience and machine learning. It introduces SOFO, a novel second-order optimization method that significantly improves training of recurrent neural networks (RNNs) for complex tasks. Its superior performance over existing methods, especially for long time horizons and noisy systems, opens exciting avenues for modeling brain dynamics and advancing AI.
Visual Insights#
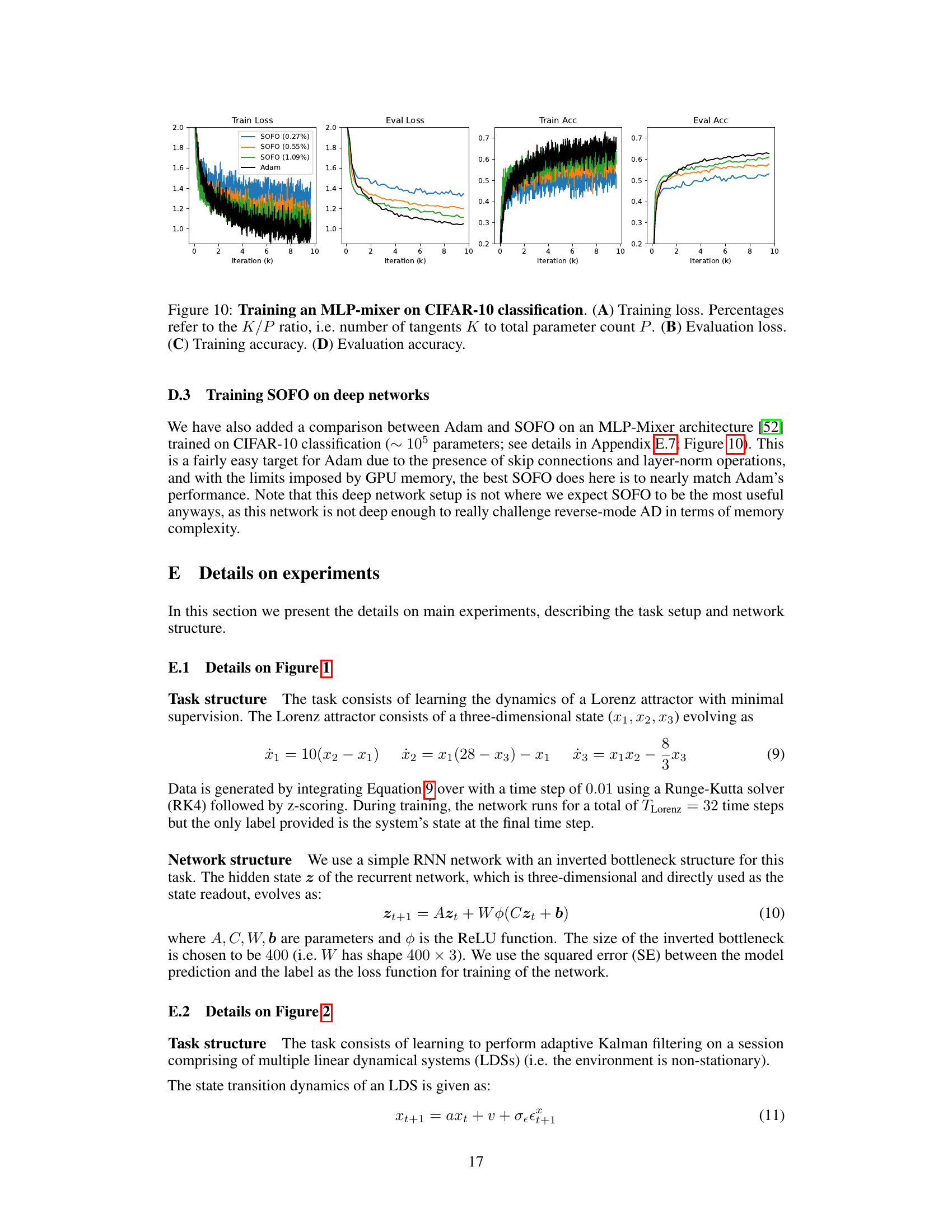
This figure shows the results of training a recurrent neural network (RNN) to learn the dynamics of a Lorenz attractor using only sparse supervision. Panel A illustrates the training paradigm, where the RNN is initialized at a random point on the Lorenz manifold and only the final state of a 32-step trajectory is used as a target. Panel B compares the learning curves of Adam, SOFO, a first-order gradient method (FGD), and a first-order version of SOFO on this task. SOFO shows faster convergence and a lower minimum loss than Adam. Panel C presents an example trajectory generated by the trained RNN, demonstrating its ability to accurately reproduce the Lorenz attractor dynamics.

This table shows the parameters used to generate the data for the adaptive Kalman filter task in Section 4.2 of the paper. It specifies the values for the time horizon (T), the fixed duration before context switches (Tfix), the survival time of each context (d), and the probability distributions for the parameters of the linear dynamical systems (LDSs) used in the task. Specifically, it details the uniform distributions from which the mean (b), the survival time (τ), the observation noise variance (σβ), and the process noise variance (σ) are sampled.
In-depth insights#
SOFO Optimizer#
The SOFO optimizer, a novel second-order method for training recurrent neural networks (RNNs), presents a compelling alternative to traditional gradient-based approaches. SOFO’s core innovation lies in its use of forward-mode automatic differentiation, enabling efficient computation of Generalized Gauss-Newton updates within randomly sampled low-dimensional subspaces. This strategy avoids the memory limitations associated with backpropagation through time (BPTT), making it particularly well-suited for tasks involving long temporal dependencies. By avoiding BPTT, SOFO is highly parallelizable, offering a significant speed advantage, especially on GPUs. Experimental results demonstrate SOFO’s superior performance on several challenging RNN tasks compared to Adam, a popular first-order optimizer, notably in tasks involving long horizons and sparse supervision. However, the algorithm’s performance is dependent on the dimensionality of the parameter space and the size of the randomly sampled subspace. While efficient for low-dimensional models, scaling to significantly larger networks may require further optimization. Despite this limitation, SOFO’s ability to handle long-range dependencies and its inherent parallelizability makes it a promising tool for applications where memory constraints and computational efficiency are paramount.
RNN Training#
Recurrent Neural Networks (RNNs), while powerful for modeling sequential data, present significant training challenges. Standard backpropagation through time (BPTT), though effective for shorter sequences, suffers from vanishing/exploding gradients and memory limitations when applied to long sequences, common in neuroscience applications. This necessitates the exploration of alternative optimization strategies. The paper investigates second-order optimization methods, particularly focusing on a novel approach called SOFO (Second-order Forward-mode Optimization). SOFO cleverly addresses memory constraints by leveraging forward-mode automatic differentiation, enabling efficient parallel computation and a constant memory footprint irrespective of sequence length. SOFO’s efficacy is demonstrated across diverse neuroscience tasks, showcasing superior performance compared to Adam, a widely used first-order optimizer. The results highlight the potential of SOFO in unlocking the modeling capabilities of RNNs for complex and long-horizon neural dynamics, particularly where traditional methods struggle.
Neuroscience Tasks#
The paper investigates the application of a novel second-order optimization algorithm, SOFO, to various neuroscience tasks. These tasks are specifically designed to push the boundaries of RNN training, addressing challenges like long time horizons and complex temporal dependencies. The focus is on RNNs as models of brain dynamics, which imposes biological plausibility constraints on the model structure, unlike in machine learning. SOFO’s performance is compared to Adam, showcasing significant improvements across several challenging neuroscience benchmarks: inferring dynamics from sparse observations, learning an adaptive Kalman filter, and a 3-bit flip-flop task. Furthermore, the algorithm excels at demanding motor tasks, including single and double-reaching paradigms which require precise temporal control and integration of sensory feedback. The superior performance is attributed to SOFO’s efficient use of parallel processing and its ability to navigate complex loss surfaces without reliance on backpropagation, which is memory-intensive. The results demonstrate SOFO’s promise in advancing research on biologically realistic neural network models for neuroscience applications.
Forward-Mode AD#
Forward-mode Automatic Differentiation (AD) offers a compelling alternative to the traditional reverse-mode AD (backpropagation) prevalent in training neural networks. Forward-mode AD computes the Jacobian-vector product (JVP), providing the sensitivity of the network’s output to changes in each parameter. Unlike reverse-mode AD, which accumulates gradients backward through the computational graph, forward-mode AD directly calculates the derivative in a single forward pass. This characteristic makes it particularly attractive for scenarios such as training recurrent neural networks (RNNs) over long time horizons where memory constraints imposed by reverse-mode AD become prohibitive. The inherent parallelizability of forward-mode AD allows for efficient computation on GPUs, leveraging the inherent parallelism of modern hardware to accelerate the training process. While the computational cost of forward-mode AD scales linearly with the number of parameters, unlike reverse-mode AD which scales with the number of outputs, this disadvantage is mitigated by employing subspace optimization techniques. By targeting only a small subset of parameters at each iteration, the computational burden is reduced to a manageable level, while retaining the benefits of second-order information obtained from the JVP computation. The ability to utilize batching of Jacobian-vector products further enhances the efficiency and scalability of forward-mode AD, making it a powerful tool for training complex models and potentially overcoming the limitations of traditional backpropagation.
Future Research#
Future research directions stemming from this work on SOFO (Second-order Forward-mode Optimization) for recurrent neural networks (RNNs) are plentiful. Extending SOFO to handle larger networks and datasets is crucial for broader applicability in machine learning, beyond the neuroscience-focused tasks examined here. Investigating adaptive damping strategies could further enhance SOFO’s robustness and efficiency, particularly in dealing with ill-conditioned loss surfaces. A deeper exploration of the algorithm’s theoretical properties is needed to fully understand its convergence behavior and potential limitations. Furthermore, applying SOFO to other challenging machine learning tasks, such as those involving complex temporal dependencies or high-dimensional data, would showcase its versatility. Finally, analyzing the biological plausibility of SOFO in light of recent neuroscience findings on synaptic plasticity could lead to valuable insights into brain function, enhancing its utility as a computational model of the brain.
More visual insights#
More on figures
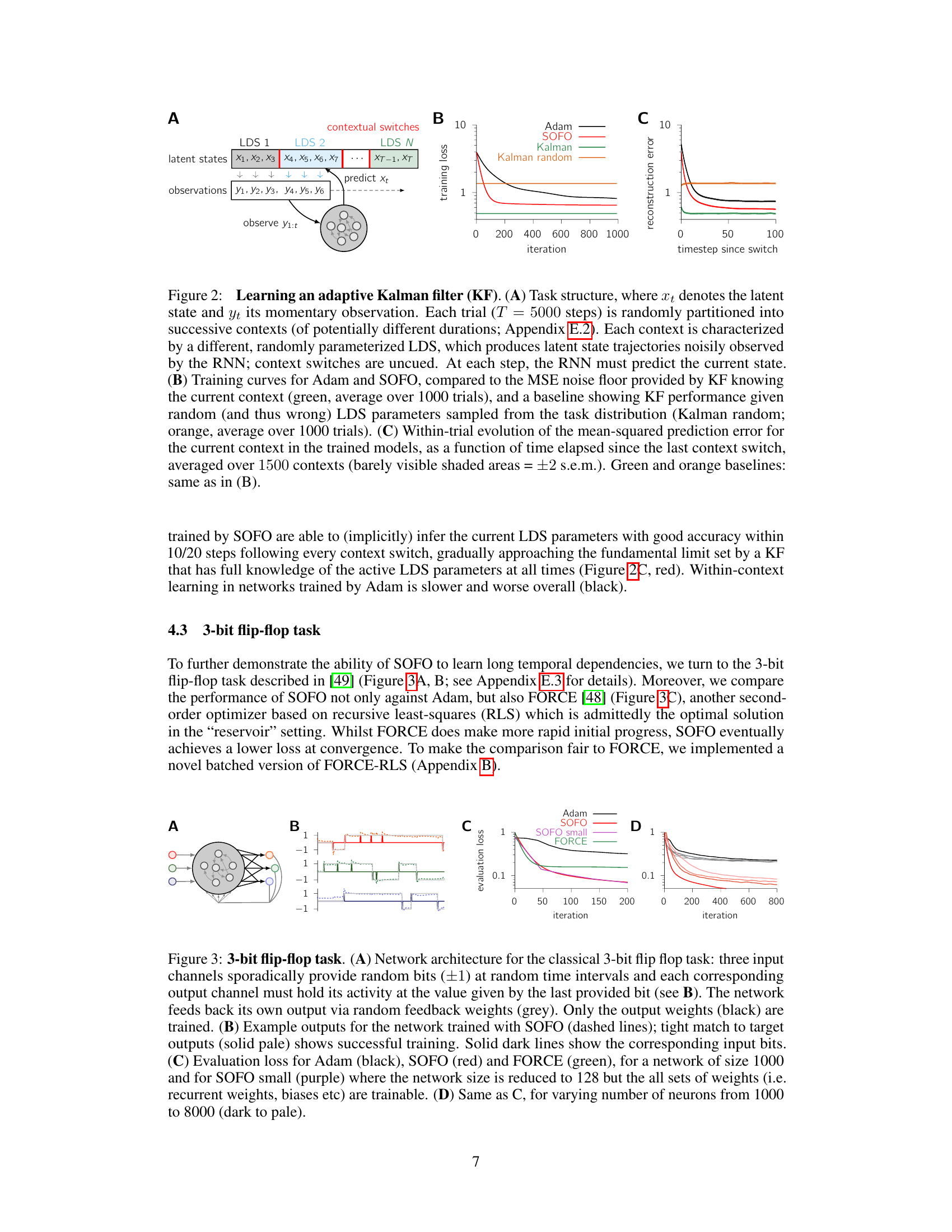
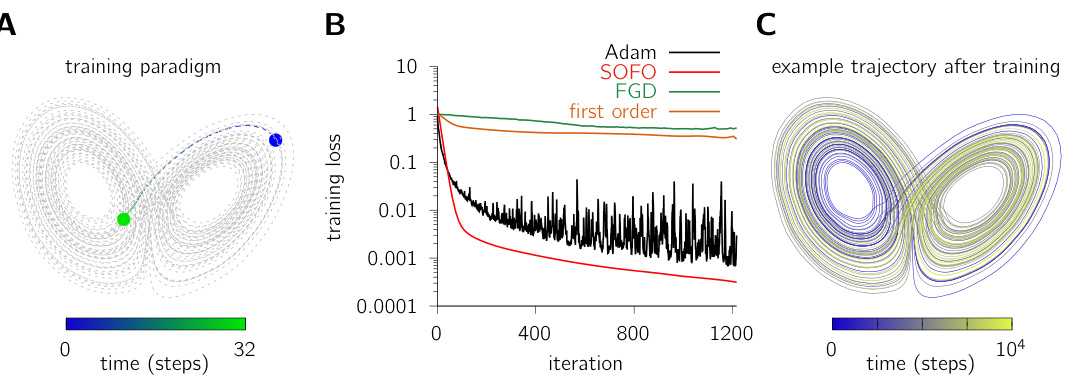
This figure shows the results of training RNNs to perform adaptive Kalman filtering in a non-stationary environment. Panel A illustrates the task structure, showing an RNN receiving noisy observations from a linear dynamical system (LDS) whose parameters change over time. Panel B compares the training loss curves for Adam and SOFO optimizers against baselines. Panel C shows the mean squared prediction error over time after a context switch, demonstrating that SOFO leads to faster learning and better performance.

Figure 3 demonstrates the performance of SOFO on the 3-bit flip-flop task, comparing it against Adam and FORCE. Panel A shows the network architecture. Panel B shows example outputs illustrating successful training with SOFO. Panels C and D display loss curves across various network sizes, demonstrating SOFO’s superior performance and ability to handle smaller networks.
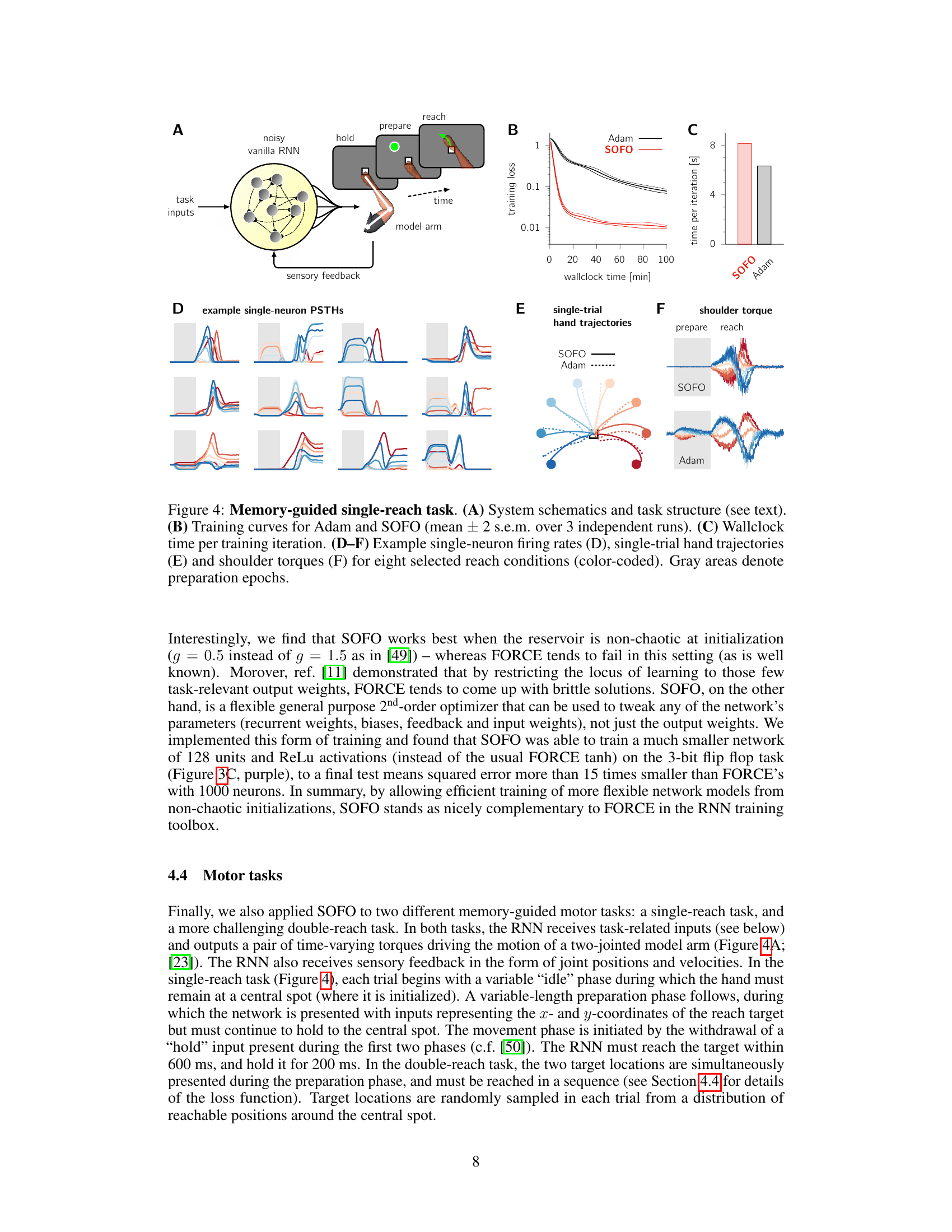
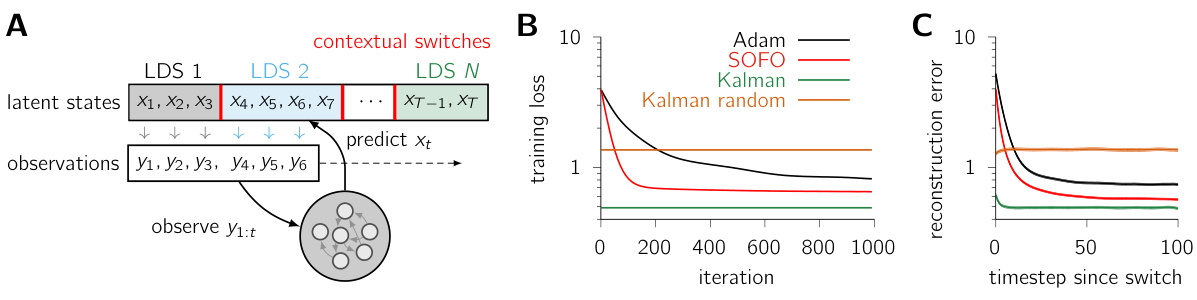
This figure shows the results of applying SOFO and Adam to a single-reach task. Panel A provides a schematic of the experimental setup, illustrating a recurrent neural network controlling a simulated two-jointed arm. Panel B displays learning curves, demonstrating that SOFO converges significantly faster than Adam. Panel C shows the wall-clock time per iteration, highlighting SOFO’s efficiency. Panels D-F present example data from a successful SOFO training run: (D) shows single-neuron peristimulus time histograms (PSTHs) for eight different reach conditions. (E) displays single-trial hand trajectories, and (F) shows the shoulder torques during a single trial. Gray shaded areas in (D) and (F) indicate the preparation phase, while the reach phase is marked in (E).

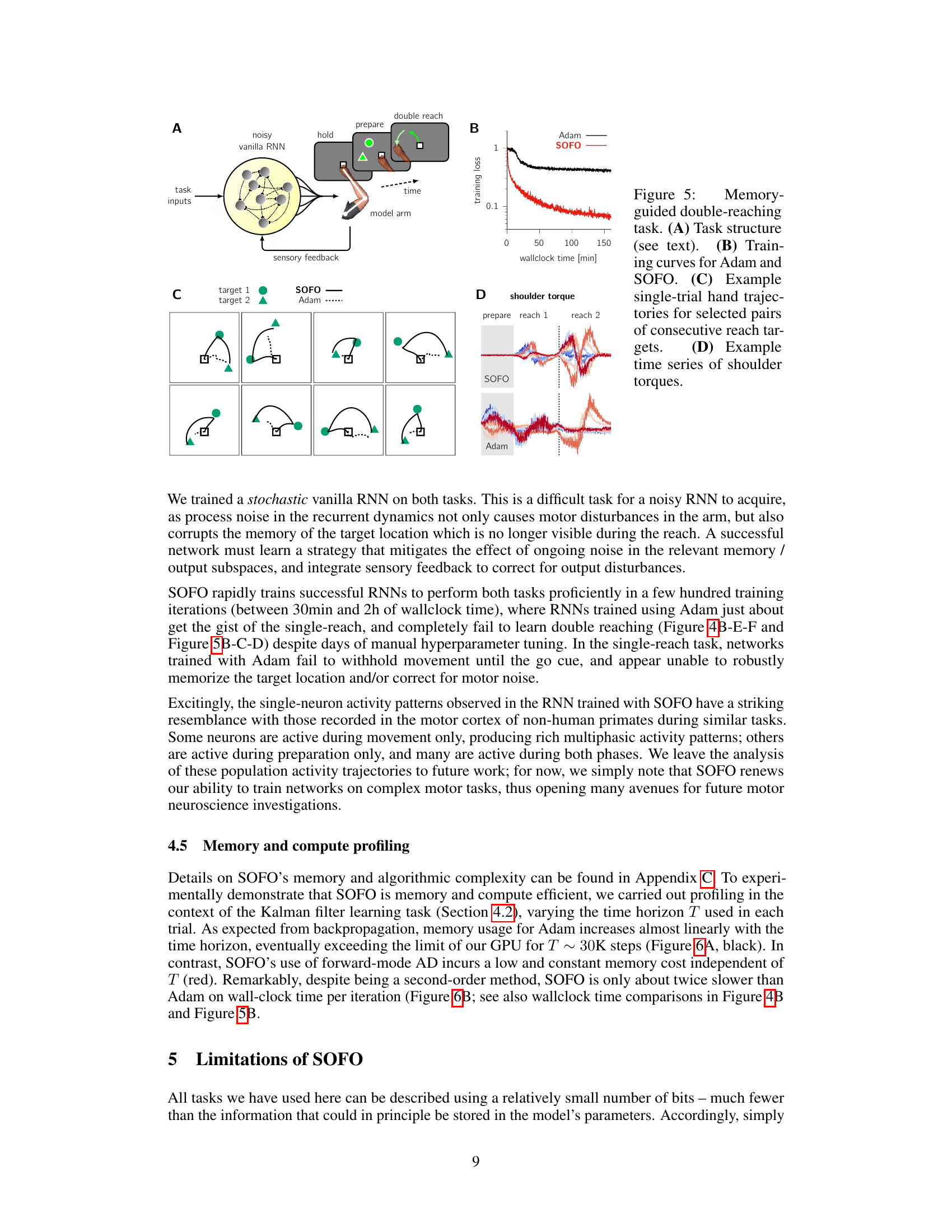
This figure demonstrates the results of applying SOFO and Adam to a memory-guided double-reaching task. Panel A shows a schematic of the task setup, where a robotic arm must reach two targets in sequence after a preparation period. Panel B presents the training curves showing SOFO’s superior performance over Adam. Panel C shows example hand trajectories generated by both optimizers highlighting SOFO’s better accuracy and smoother movements. Finally, panel D displays shoulder torques to illustrate the difference in motor control strategies.

This figure shows the results of an experiment comparing the memory usage and wall-clock time per iteration of the Adam and SOFO optimizers. The experiment used the Kalman filter task from Section 4.2 of the paper with different time horizons (T). The figure shows that the SOFO optimizer is more memory-efficient than Adam and has comparable wall-clock time per iteration.

Figure 7 shows the results of a one-shot classification task. Panel A illustrates the task structure, which involves a learning phase where the network is exposed to a set of three input/output pairs, followed by an exploitation phase where the network is tested on three new inputs. Panel B displays the learning curve of one-shot classification accuracy for both Adam and SOFO optimizers during training, demonstrating SOFO’s superior performance.

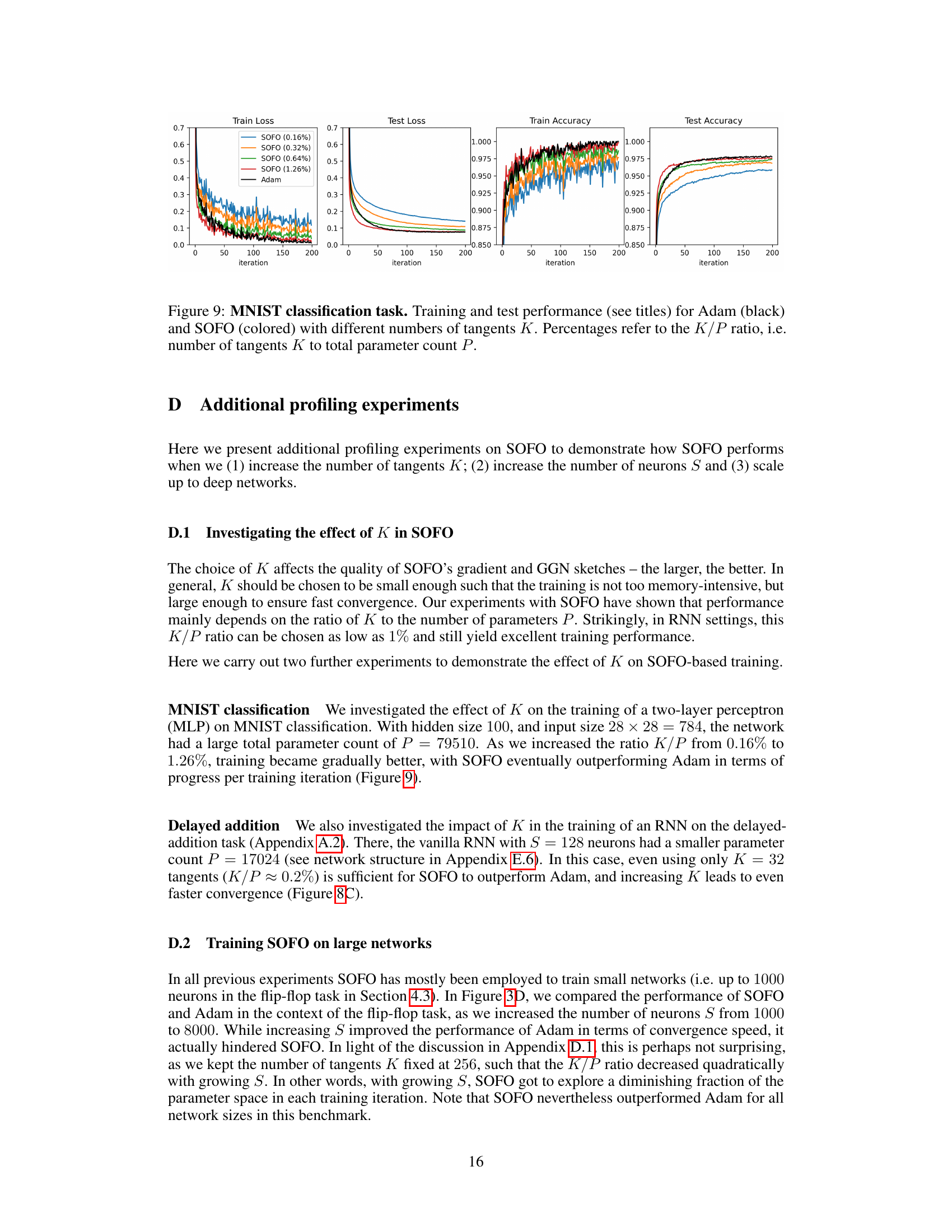
This figure shows the training and testing performance of Adam and SOFO optimizers on the MNIST classification task. Different lines represent SOFO with varying numbers of tangents (K), expressed as a percentage of the total number of parameters (P). The plots show training and testing loss, as well as training and testing accuracy over 200 training iterations. The figure demonstrates that SOFO, even with a relatively small number of tangents, can achieve comparable or better performance than Adam on this classification task.
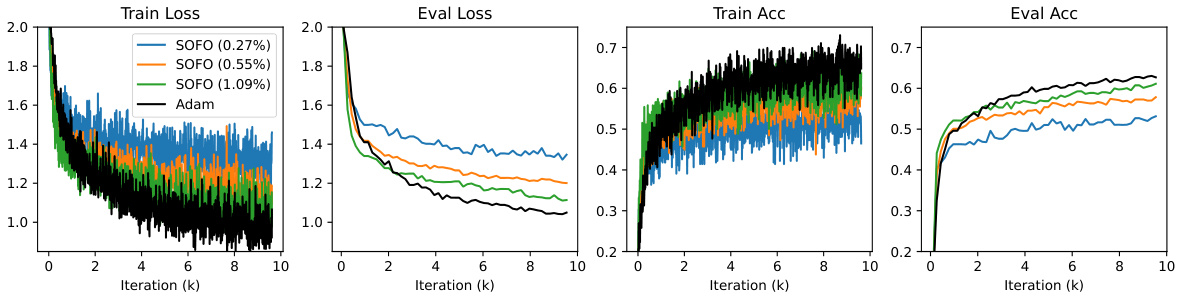
The figure shows the training and test performance of Adam and SOFO on the MNIST classification task with different numbers of tangents K. The left two panels display training and test loss, while the right two panels show training and test accuracy. The results show that SOFO outperforms Adam, particularly as the number of tangents (K) increases. The K/P ratio (number of tangents K to total parameter count P) is also shown in the legend, indicating the fraction of parameters updated at each step. This experiment demonstrates the impact of the number of tangents on the performance of SOFO.
More on tables
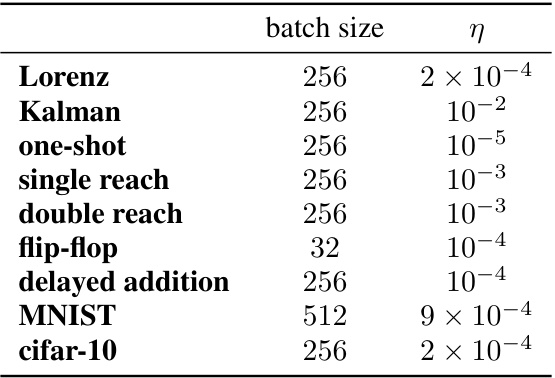
This table shows the hyperparameter settings used for the Adam optimizer across different tasks in the paper. It lists the batch size and learning rate (η) used for each task. The learning rate is a crucial hyperparameter that controls the step size during the optimization process.
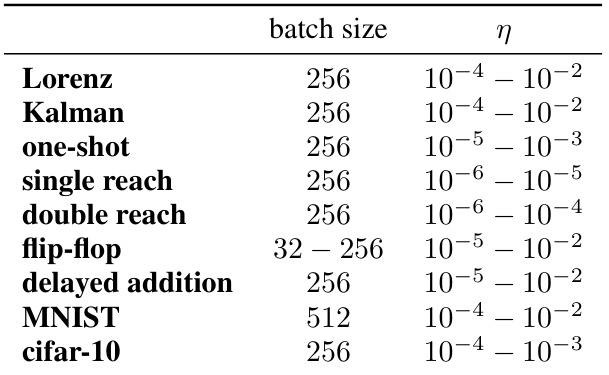
This table shows the ranges of hyperparameter values explored for the Adam optimizer across various tasks in the paper. The hyperparameters include the batch size and the learning rate (η). The table provides the ranges tested for each task, allowing for a better understanding of the parameter search space explored during the experiments.

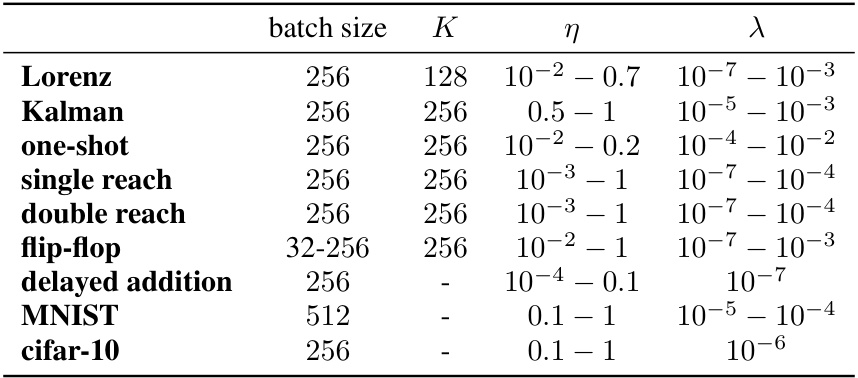
This table presents the hyperparameters used for the SOFO optimizer in various experiments presented in the paper. It shows the batch size, the number of tangents (K), the ratio of K to the total number of parameters (K/P), the learning rate (η), and the relative damping parameter (λ). Note that for some experiments, a range of K values were tested, hence the empty entries.
This table shows the ranges of hyperparameters used in the experiments for the SOFO optimizer. The hyperparameters include batch size, the number of tangents (K), the learning rate (η), and the relative damping parameter (λ). Each row represents a different task used in the experiments, showing the range of values explored for each hyperparameter in that specific task. The table is crucial for understanding the range of parameter settings used to find the optimal configurations for SOFO across various experiments.

This table shows the hyperparameters used for three different optimizers: FGD, first-order SOFO, and batched FORCE. It indicates the batch size, the number of tangents (K, relevant only to SOFO), the learning rate (η), the range of learning rates explored during hyperparameter search, and the range of α values (only for batched FORCE). The optimizers are applied to two different tasks: the Lorenz task and the 3-bit flip-flop task. The table helps clarify the settings used in the experiments for each optimizer and task.
Full paper#