↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
PAC-Bayesian analysis, a frequentist approach incorporating prior knowledge into learning, has been hindered by the inability to sequentially update priors without losing confidence information. Existing methods lose confidence information accumulated in prior updates, limiting the benefits of sequential processing and resulting in looser final bounds. This is because confidence intervals rely solely on data points not used in prior construction, ignoring valuable information contained within the prior itself.
This paper introduces Recursive PAC-Bayes, a novel approach that overcomes this limitation. It uses a novel decomposition of the expected loss of randomized classifiers, enabling sequential prior updates without information loss. The method recursively bounds prior losses, incorporating data used to build the prior for improved accuracy and tighter bounds. Empirical results show that this new approach substantially outperforms existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with PAC-Bayes bounds and sequential learning. It directly addresses the long-standing challenge of sequentially updating priors without information loss, offering significant improvements in bound tightness and empirical performance. This opens avenues for improved generalization bounds in various machine learning settings.
Visual Insights#
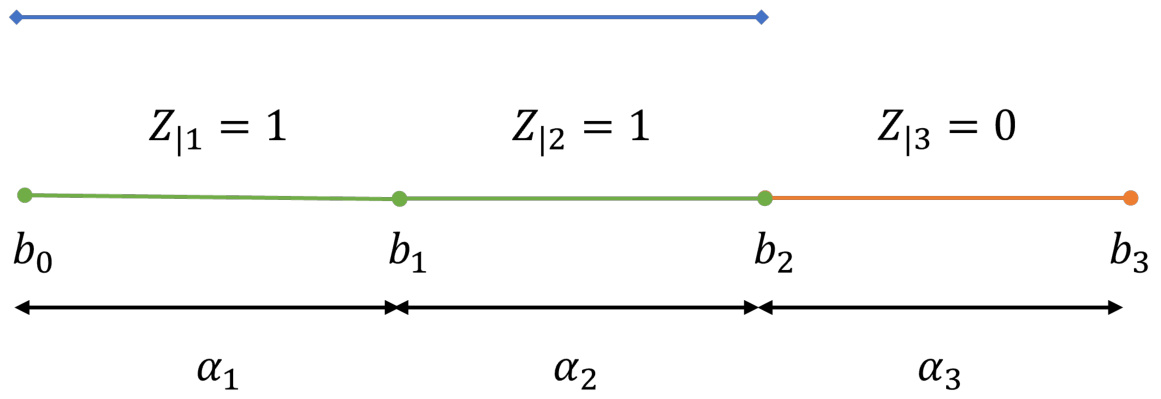
This figure illustrates how a discrete random variable Z can be decomposed into a sum of binary random variables. The decomposition is analogous to a progress bar, where each segment represents a binary variable indicating whether the value is above a certain threshold. The sum of these binary variables weighted by the length of each segment equals the value of the discrete random variable. This decomposition is useful for deriving tighter concentration inequalities.
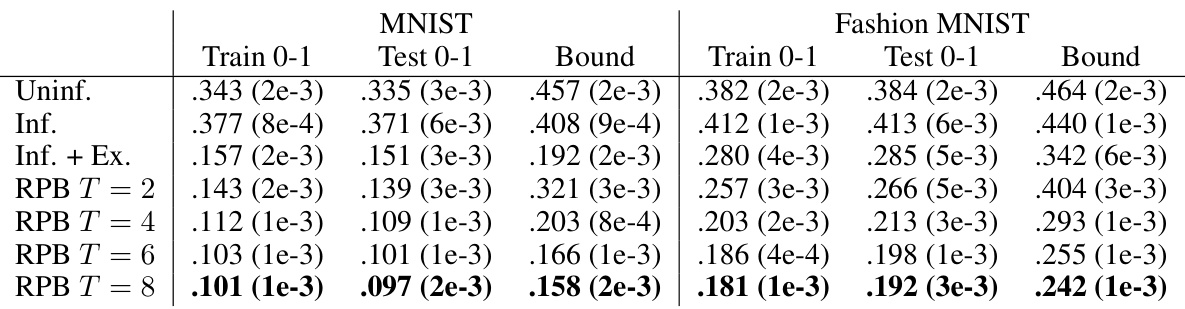
This table presents a comparison of different PAC-Bayes approaches on MNIST and Fashion MNIST datasets. It shows the training and testing classification error (0-1 loss) for each method, along with the corresponding generalization bounds. The methods compared are Uninformed priors, Data-informed priors, Data-informed priors with excess loss, and the proposed Recursive PAC-Bayes method with varying recursion depths (T). The results are averaged over 5 repetitions, with standard deviations reported.
In-depth insights#
PAC-Bayes Evolution#
The evolution of PAC-Bayes bounds reflects a continuous effort to tighten generalization guarantees by incorporating prior knowledge more effectively. Early methods used uninformed priors, leading to loose bounds. The introduction of data-informed priors improved the bounds’ tightness by using part of the data to shape the prior, but this came at the cost of reduced sample size for the final bound. Subsequent work addressed this by incorporating excess loss, which further refines the bound and utilizes data more efficiently. The crucial contribution of Recursive PAC-Bayes lies in its ability to achieve sequential prior updates without information loss, thus fully leveraging data and providing significantly tighter bounds than previous methods. This represents a fundamental shift in how prior information is integrated, making sequential learning with PAC-Bayes significantly more efficient and effective.
Recursive PAC-Bayes#
Recursive PAC-Bayes presents a novel frequentist approach to sequentially update prior knowledge in machine learning without information loss. Unlike previous methods, it avoids the problem of confidence intervals depending solely on the final data batch, retaining information from prior updates. This is achieved through a novel decomposition of the expected loss, recursively bounding prior losses and excess posterior losses, preserving information along the way. The method’s effectiveness is demonstrated empirically, outperforming existing techniques. A key contribution is a generalization of split-kl inequalities to discrete random variables, crucial for its theoretical grounding and performance. This recursive framework fundamentally shifts the PAC-Bayes paradigm, enabling more efficient and powerful learning with data-informed priors.
Loss Decomposition#
The core idea of the paper hinges on a novel loss decomposition technique. Instead of directly bounding the posterior’s expected loss, the authors cleverly decompose it into two components: an excess loss term and a prior loss term. This decomposition is crucial because it allows for recursive bounding. The excess loss represents the difference between the posterior’s loss and a scaled-down version of the prior’s loss, while the prior loss itself is recursively bounded, using previously accumulated information. This recursive bounding prevents information loss in sequential prior updates, which is a significant improvement over existing PAC-Bayes approaches. The efficacy of this decomposition is demonstrated empirically and theoretically by improved generalization bounds. This strategic breakdown enables the introduction of a powerful recursive bound and constitutes a major theoretical contribution of the paper.
Empirical Evaluation#
An empirical evaluation section in a research paper should rigorously assess the proposed method’s performance. It needs to compare the novel approach against relevant baselines using appropriate metrics. The evaluation should be conducted on diverse datasets to demonstrate generalizability. The section must include details on the experimental setup (datasets, hyperparameters, etc.) to ensure reproducibility. Statistical significance testing is critical to confirm observed performance differences aren’t due to chance. Furthermore, clear visualization of results, such as graphs and tables, aids comprehension. A thoughtful discussion section interpreting the results and addressing any limitations in the experimental design is crucial for a robust evaluation. Finally, the presentation must be concise and well-structured, focusing on the most relevant findings and supporting them with strong evidence. A well-executed empirical evaluation section provides a strong foundation for validating the paper’s claims.
Future Directions#
The research on Recursive PAC-Bayes opens exciting avenues. Extending the framework to handle unbounded losses would broaden its applicability to a wider range of machine learning tasks. Investigating alternative data splitting strategies beyond the geometric approach used in the experiments could lead to improved performance and efficiency. A key area for future work is developing more efficient optimization techniques for the recursive bounds, potentially leveraging advances in convex optimization or approximation methods. Finally, applying Recursive PAC-Bayes to more complex learning settings, such as online learning or reinforcement learning, presents a significant challenge and opportunity to advance the state-of-the-art in generalization bounds. Exploring the theoretical connections between the Recursive PAC-Bayes approach and other sequential learning frameworks could unlock further insights and provide a more unified perspective on sequential learning theory.
More visual insights#
More on tables

This table compares the performance of four different PAC-Bayes approaches (Uninformed, Informed, Informed + Excess Loss, and Recursive PAC-Bayes) on MNIST and Fashion MNIST datasets. For each method and dataset, it shows the training and testing classification error rates (0-1 loss), along with the corresponding generalization bounds. The results are averaged over five independent runs, with standard deviations reported. The table highlights the improved performance and tighter bounds achieved by the Recursive PAC-Bayes method, particularly as the number of recursive steps increases.

This table presents a comparison of different PAC-Bayes approaches on MNIST and Fashion-MNIST datasets. It shows the training and test classification error (0-1 loss) for each method, along with the corresponding generalization bounds. The methods compared include uninformed priors, data-informed priors, data-informed priors with excess loss, and the novel recursive PAC-Bayes approach with varying recursion depths (T). The results are averaged over 5 repetitions, with standard deviations reported.

This table compares the performance of four different PAC-Bayes approaches (Uninformed, Informed, Informed + Excess Loss, and Recursive PAC-Bayes) on MNIST and Fashion MNIST datasets. For each method, it shows the training and testing classification error (0-1 loss), and the corresponding generalization bound. The results are averaged over five repetitions, with standard deviations reported.

This table compares the performance of four different PAC-Bayes methods on MNIST and Fashion MNIST datasets. The methods are Uninformed Priors, Data-Informed Priors, Data-Informed Priors + Excess Loss, and Recursive PAC-Bayes. The table shows the training and testing 0-1 loss for each method, along with the corresponding generalization bound. The Recursive PAC-Bayes method is tested with different recursion depths (T=2,4,6,8). The results are averaged over 5 repetitions, with standard deviations reported.
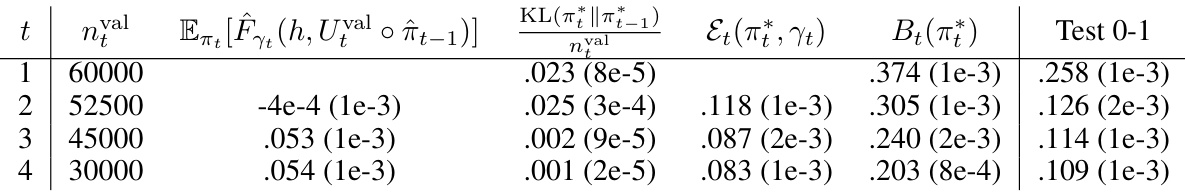
This table compares the performance of four different PAC-Bayes approaches on MNIST and Fashion MNIST datasets. It shows the training and testing classification error (0-1 loss) for each method, as well as the corresponding generalization bounds. The methods compared are Uninformed priors, Data-informed priors, Data-informed priors + excess loss, and the novel Recursive PAC-Bayes method with varying recursion depths (T=2,4,6,8). The results demonstrate the improved performance and tighter bounds of the Recursive PAC-Bayes approach, particularly as the recursion depth increases.

This table compares the performance of four different PAC-Bayes approaches on MNIST and Fashion MNIST datasets. The methods compared are: Uninformed priors, Data-informed priors, Data-informed priors + excess loss, and Recursive PAC-Bayes. The table shows the training and testing error rates (0-1 loss) and the corresponding generalization bounds for each method, averaged over five repetitions, allowing for a comparison of accuracy and the tightness of the bounds produced by each approach.
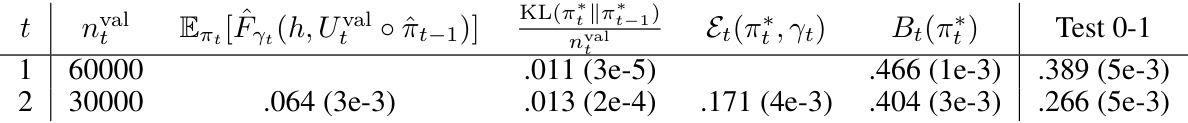
This table compares the performance of four different PAC-Bayes approaches (Uninformed, Informed, Informed+Excess Loss, and Recursive PAC-Bayes) on MNIST and Fashion MNIST datasets. For each method, it shows the training and testing classification error rates (0-1 loss) and the corresponding generalization bounds. The Recursive PAC-Bayes results are shown for different recursion depths (T). The table aims to demonstrate the improvement in accuracy and tighter bounds achieved by the Recursive PAC-Bayes method compared to existing approaches.
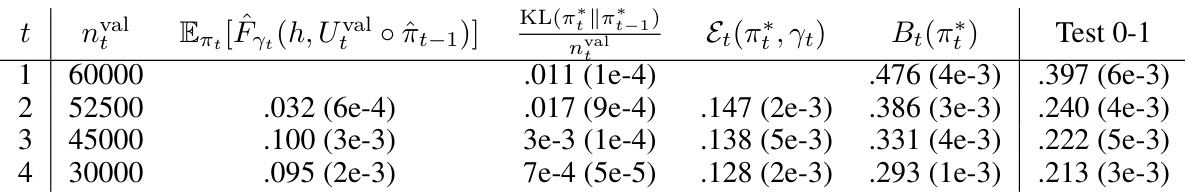
This table compares the performance of four different PAC-Bayes approaches on MNIST and Fashion MNIST datasets. It shows the training and testing classification error (0-1 loss) for each method, along with the corresponding generalization bounds. The methods compared include the uninformed prior approach, data-informed priors, data-informed priors with excess loss, and the proposed recursive PAC-Bayes approach with varying recursion depths (T=2, 4, 6, 8). The results are averaged over five repetitions and include standard deviations.

This table compares the performance of four different PAC-Bayes approaches on MNIST and Fashion MNIST datasets. It shows the training and testing classification error rates (0-1 loss) achieved by each method, along with their corresponding generalization bounds. The methods compared are Uninformed priors, Data-informed priors, Data-informed priors + excess loss, and the novel Recursive PAC-Bayes method with varying recursion depths (T). The table presents the mean and standard deviation of these metrics across five repetitions.

This table compares the performance of four different methods for classification on the MNIST and Fashion MNIST datasets. It shows the training and testing error rates (0-1 loss) for each method, along with the corresponding PAC-Bayes bounds. The methods compared are Uninformed priors, Data-informed priors, Data-informed priors + excess loss, and the Recursive PAC-Bayes approach with different recursion depths (T=2,4,6,8).

This table presents a comparison of different PAC-Bayes approaches (Uninformed, Informed, Informed + Excess Loss, and Recursive PAC-Bayes) on MNIST and Fashion MNIST datasets. It shows the training and testing classification error rates (0-1 loss) and the corresponding generalization bounds obtained by each method. The results are averaged over 5 repetitions, and standard deviations are provided. Recursive PAC-Bayes is tested with varying recursion depths (T).
Full paper#