Geodesic Optimization for Predictive Shift Adaptation on EEG data

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with EEG data, particularly in multi-center studies. GOPSA offers a novel solution to a significant challenge in EEG analysis: handling distribution shifts in both data and prediction targets. This method not only improves the accuracy of EEG-based predictions but also opens doors for new research on adaptive machine learning for biological signals.

Visual Insights

#

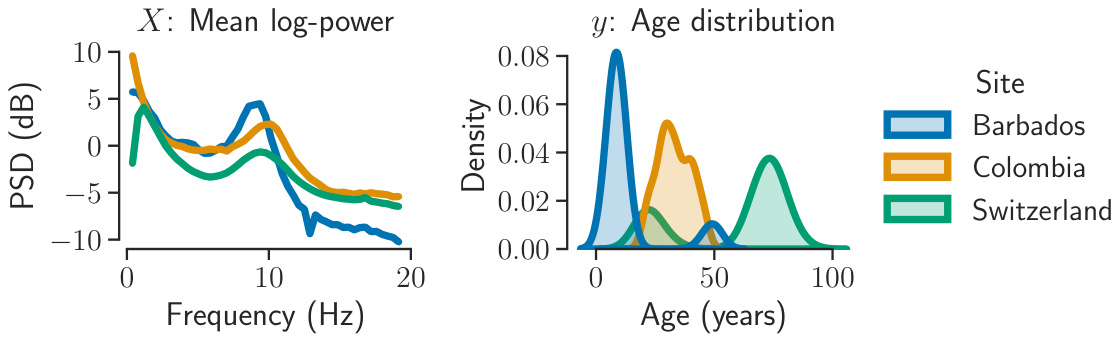
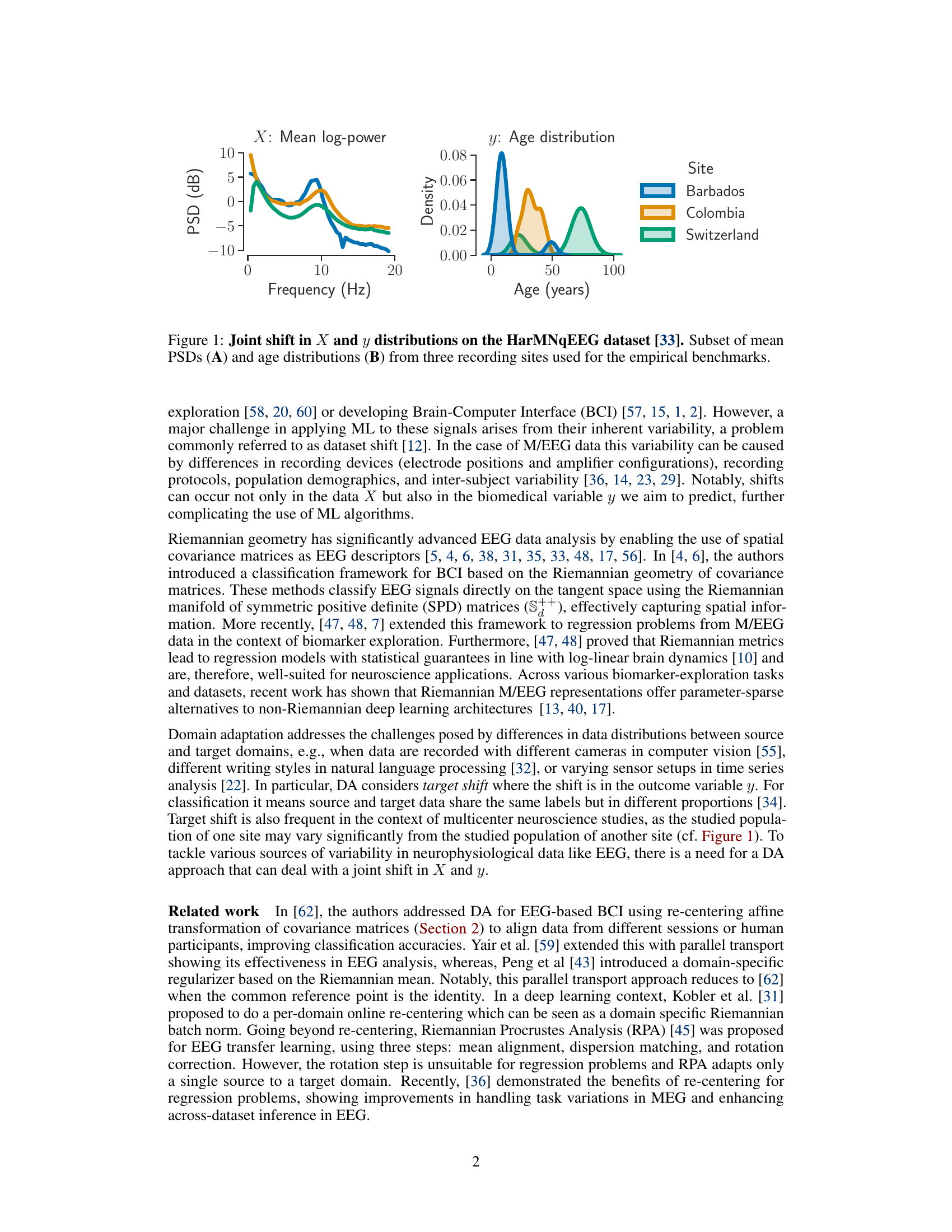
This figure shows the joint shift in data (X) and the variable of interest (y) distributions across different recording sites. The left panel displays the mean power spectral densities (PSDs) for three sites (Barbados, Colombia, and Switzerland). The right panel shows the age distributions for the same three sites. The figure illustrates how different recording sites can result in variations in both the EEG data itself and the age distribution of the participants within each site, highlighting the challenge of applying machine learning algorithms to this type of data without considering these shifts.

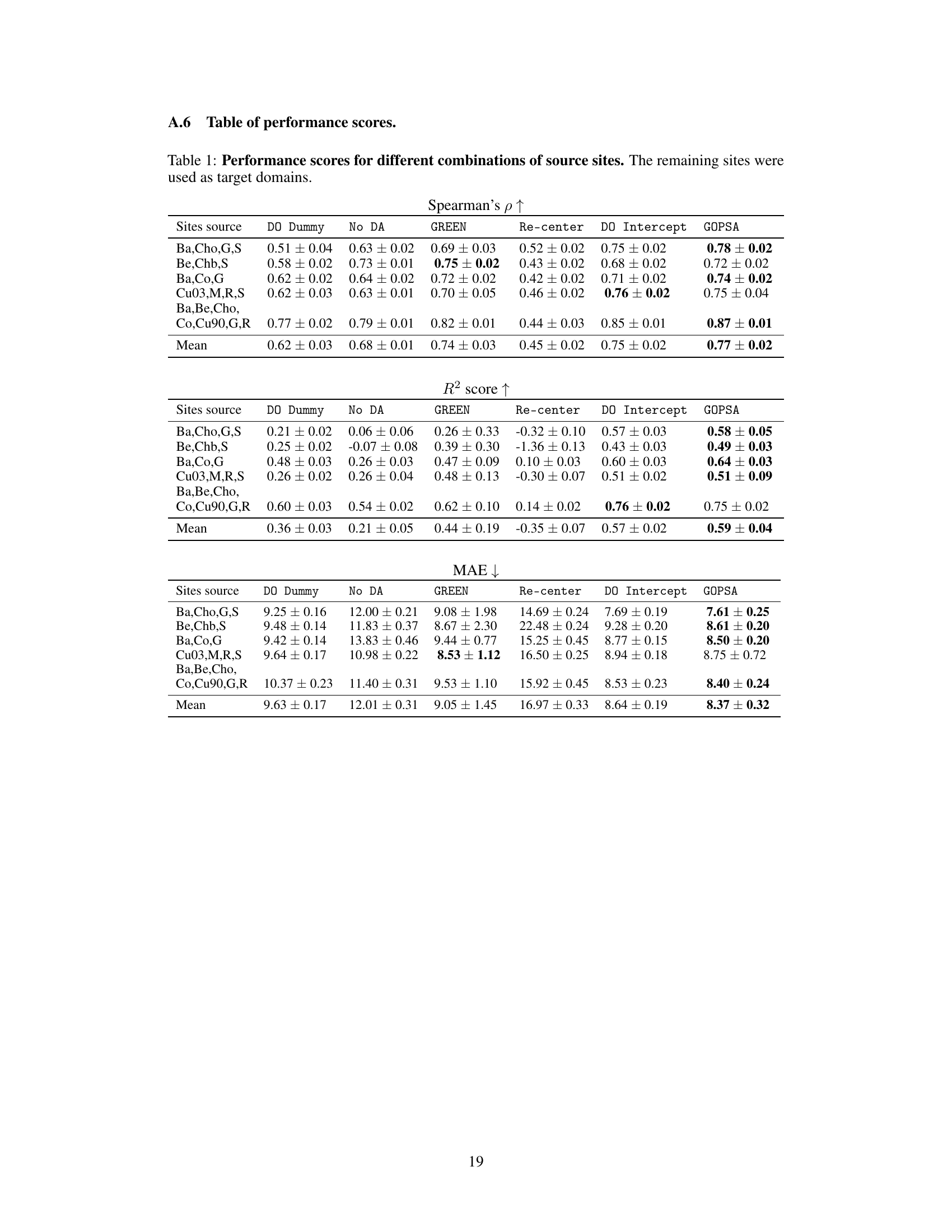
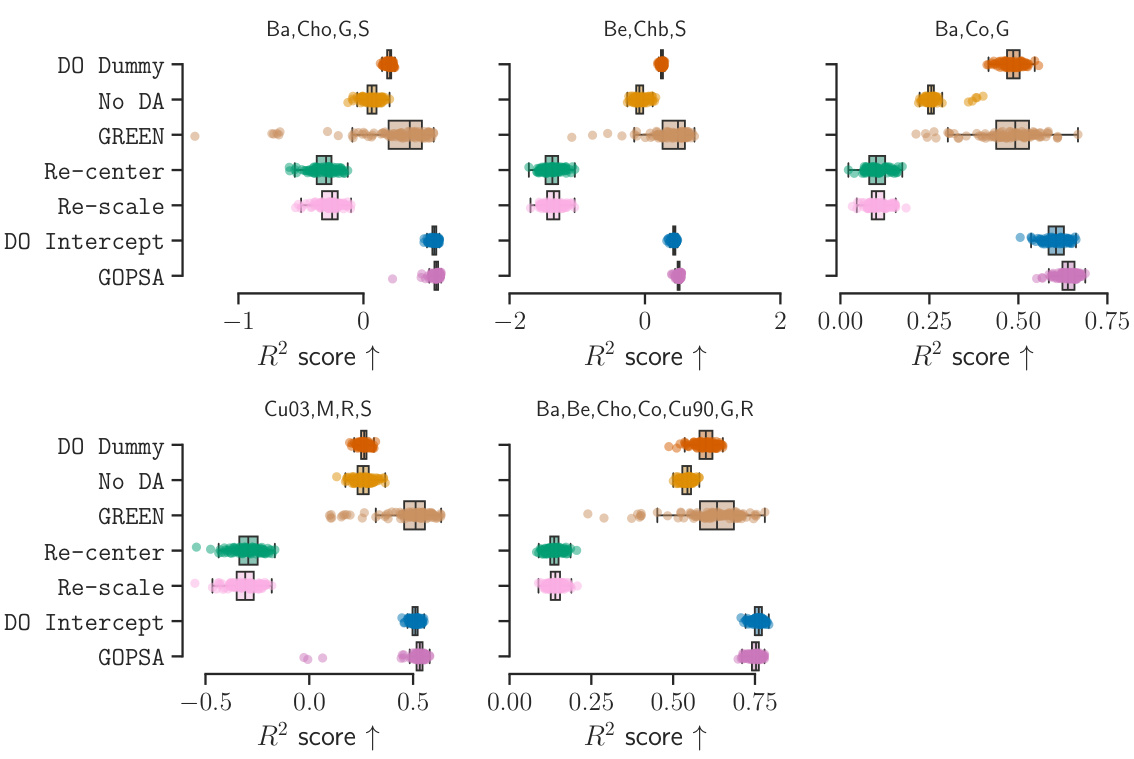
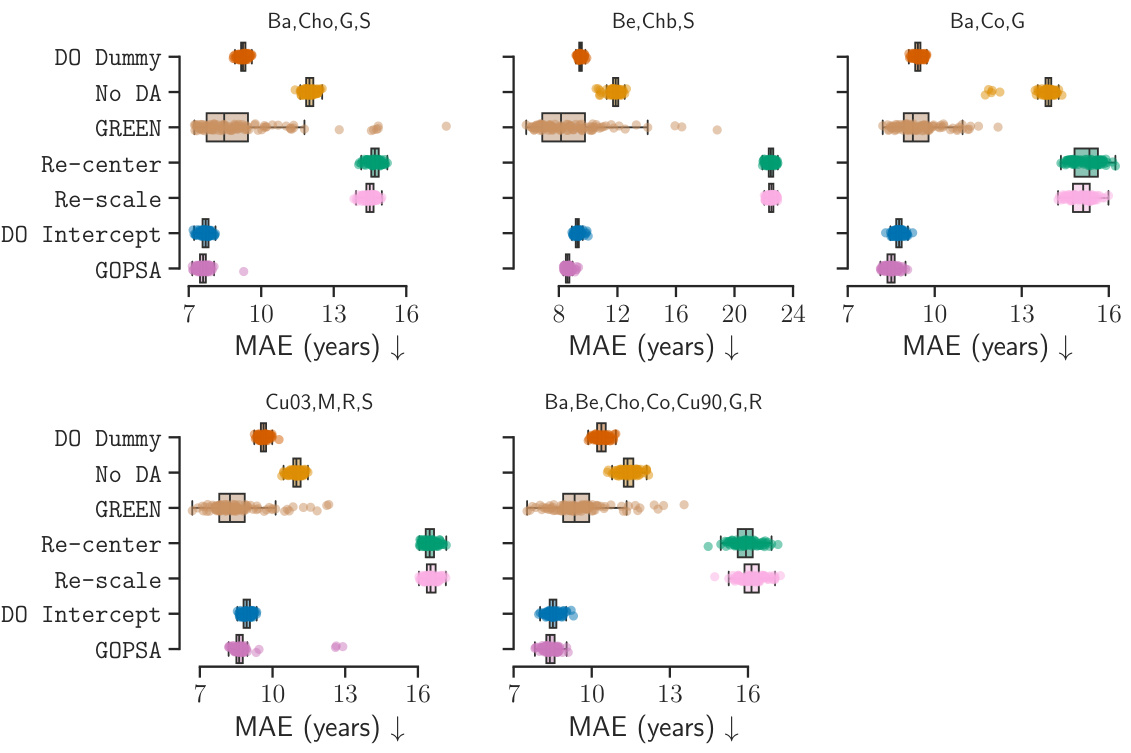
This table presents the performance scores (Spearman’s ρ, R², and MAE) for different methods (DO Dummy, No DA, GREEN, Re-center, DO Intercept, and GOPSA) across various source-target site combinations in the HarMNqEEG dataset. Each row represents a specific combination of source sites used to train the models, while the remaining sites served as target domains for evaluating the models. The table shows the mean performance and standard deviation across 100 stratified shuffle splits for each metric and method. The results are useful for comparing the effectiveness of each method in generalizing across different recording sites in the HarMNqEEG dataset.

In-depth insights

#

SPD Manifold DA

#

The concept of “SPD Manifold DA” integrates two significant areas: the Riemannian geometry of Symmetric Positive Definite (SPD) matrices and Domain Adaptation (DA) techniques. SPD matrices are particularly useful in representing covariance matrices of data, such as those found in electroencephalography (EEG). Leveraging the SPD manifold’s unique geometric structure offers advantages for DA, as traditional Euclidean-based methods often struggle with the complex relationships within covariance data. Domain adaptation becomes crucial when working with data from various sources (domains) which may exhibit differing distributions, impacting model performance. By utilizing geodesic distances and parallel transport within the SPD manifold, DA algorithms can effectively align and integrate these disparate data distributions. This approach offers a powerful framework for handling distribution shifts in EEG or other similar data where covariance information is central to analysis and prediction. The effectiveness of such methods hinges on the ability to effectively capture and model the underlying non-Euclidean geometry while simultaneously mitigating the domain shift’s influence on prediction.

GOPSA Method

#

The GOPSA method, a novel approach to predictive shift adaptation in EEG data analysis, stands out for its ability to handle simultaneous distribution shifts in both the input data (X) and the variable to predict (y). It leverages the Riemannian geometry of symmetric positive definite (SPD) matrices, representing spatial covariance structures, to tackle this complex challenge. GOPSA’s key innovation lies in its joint learning of a domain-specific re-centering operator and a global regression model. This strategy effectively addresses site-specific intercepts while maintaining a shared underlying model across diverse datasets. By using parallel transport along geodesics on the SPD manifold, GOPSA elegantly incorporates domain-specific adjustments. This results in improved prediction accuracy and enhanced generalization capabilities, particularly valuable in multi-center studies where data from different recording sites exhibits substantial variability. The method’s effectiveness has been demonstrated across multiple regression metrics (R2, MAE, Spearman’s ρ) and diverse datasets, showcasing its potential as a robust solution for test-time domain adaptation in EEG research.

HarMN-qEEG Test

#

A hypothetical ‘HarMN-qEEG Test’ section in a research paper would likely detail the empirical evaluation of a method for predictive shift adaptation on the HarMN-qEEG dataset. This would involve a rigorous experimental design, describing the chosen source and target domains, the metrics used to evaluate performance (e.g., R-squared, MAE, Spearman’s correlation), and how the results were statistically analyzed. Benchmarking against existing methods would be crucial, showing the proposed approach’s improvements or limitations compared to state-of-the-art techniques. The evaluation might also explore how performance varies under different levels of simulated or naturally occurring distribution shifts. Robustness checks, potentially involving sensitivity analysis to hyperparameter choices, would add to the credibility of the findings. Finally, the discussion might consider the generalizability of the results and implications for broader applications in real-world settings, including the practical significance for multicenter clinical trials.

Joint Shift Issue

#

The “Joint Shift Issue” in machine learning, particularly within the context of EEG data analysis, highlights the challenges posed by simultaneous distribution shifts in both the input features (X) and the target variable (y). Traditional domain adaptation methods often struggle with this scenario because they typically address shifts in either X or y independently. A joint shift implies that the relationship between X and y also changes across domains, rendering methods that only adjust for marginal distribution discrepancies ineffective. This necessitates more sophisticated techniques that can jointly model and adapt to the complex interplay between these shifts. The difficulty is compounded in EEG analysis where the data often resides on a Riemannian manifold, adding further complexity to the adaptation process. Addressing the joint shift issue effectively is critical for robust and reliable predictive models in applications like age prediction from EEG data, which involves analyzing data from diverse populations and recording settings. Developing algorithms that leverage the geometric structure of the data while simultaneously accounting for both types of shifts remains a crucial research direction for improving the generalizability and effectiveness of machine learning models for EEG data analysis.

Future works

#

Future research directions stemming from this work could explore several promising avenues. Extending GOPSA to handle more complex data structures, such as tensors or graphs, would broaden its applicability. Investigating alternative Riemannian metrics and their impact on GOPSA’s performance is crucial for optimization and robustness. Incorporating additional covariates beyond age into the prediction model would enhance its predictive power and clinical relevance. Finally, a comprehensive evaluation of GOPSA across diverse neurological conditions and datasets would further validate its efficacy and establish generalizability.

More visual insights

#

More on figures

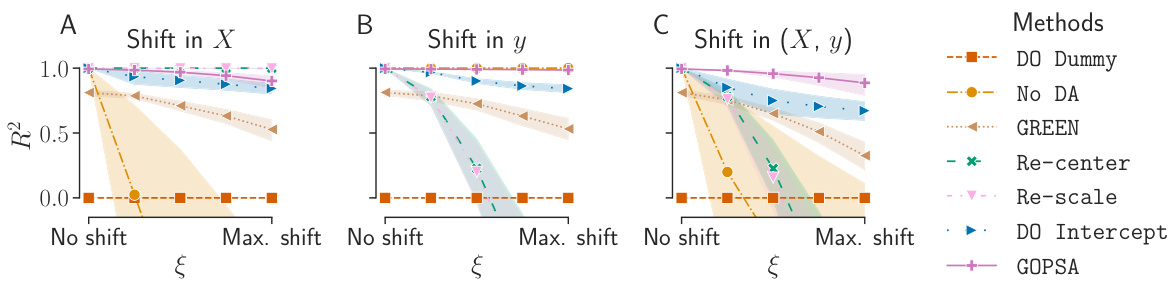
This figure displays the performance (R-squared) of different domain adaptation methods on simulated data under various conditions of data shift. The x-axis represents the magnitude of the shift (ξ), ranging from no shift to a maximum shift. The three subfigures (A, B, C) show results for shifts applied to the covariance matrices (X), the variances of the underlying signal (y), and both simultaneously (X, y), respectively. The y-axis shows the R-squared values, a metric representing the goodness of fit of the models. The different colored lines represent different domain adaptation methods. The figure demonstrates how the performance of each method changes as the shift increases, illustrating the effects of various types of data shifts.

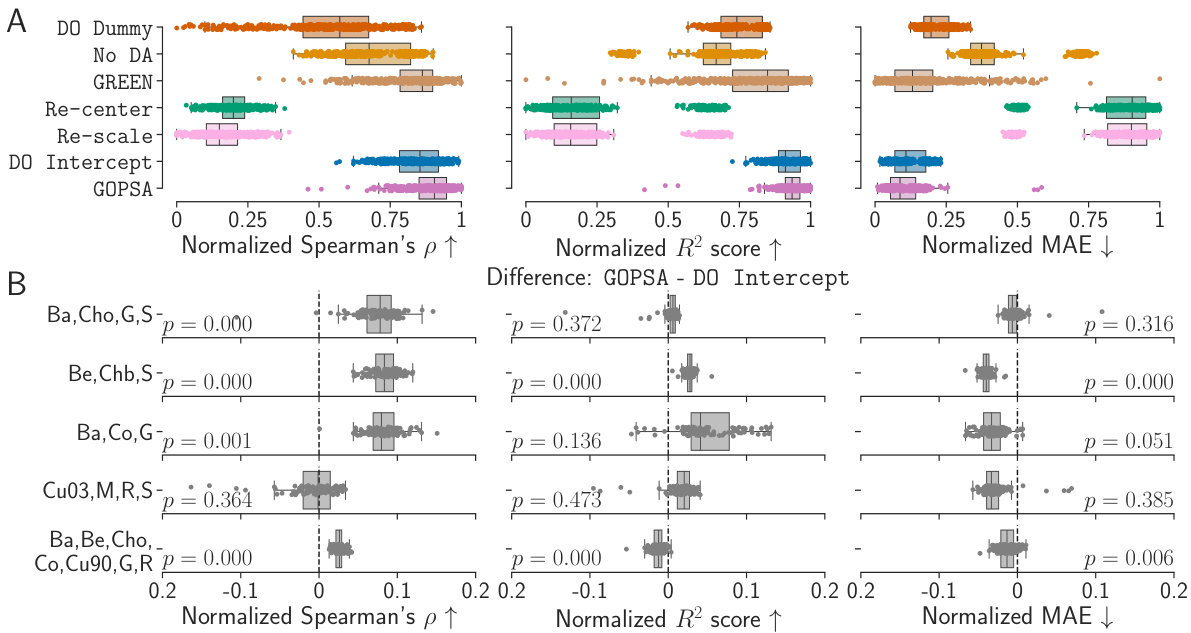
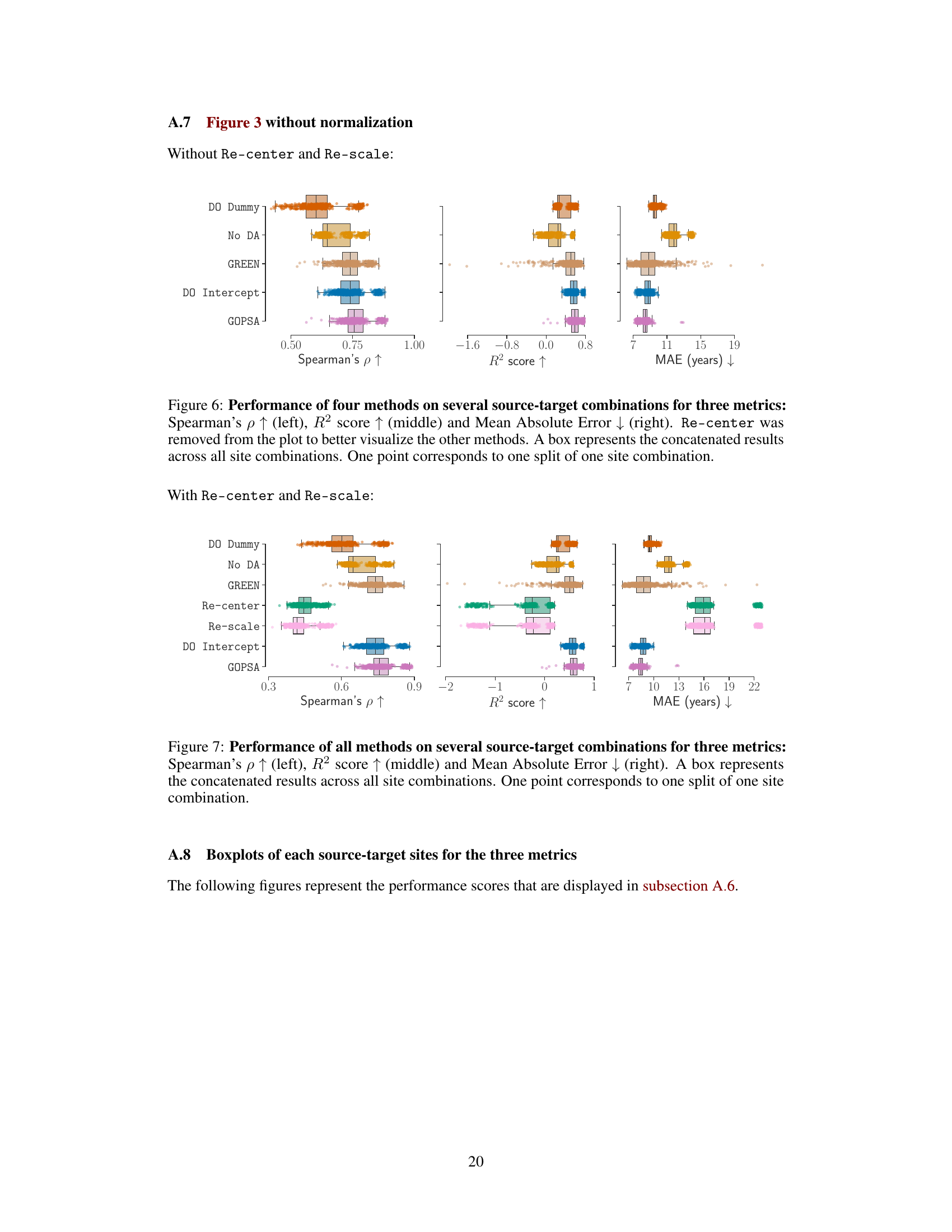
This figure displays the results of the empirical benchmarks of GOPSA on the HarMNqEEG dataset. It shows the performance of GOPSA and other baseline methods across several source-target site combinations, using three evaluation metrics: Spearman’s ρ, R², and MAE. The results are normalized using min-max scaling for better comparison. Panel A presents boxplots of the normalized scores for all methods. Panel B shows the difference between GOPSA and DO Intercept, highlighting statistically significant differences.

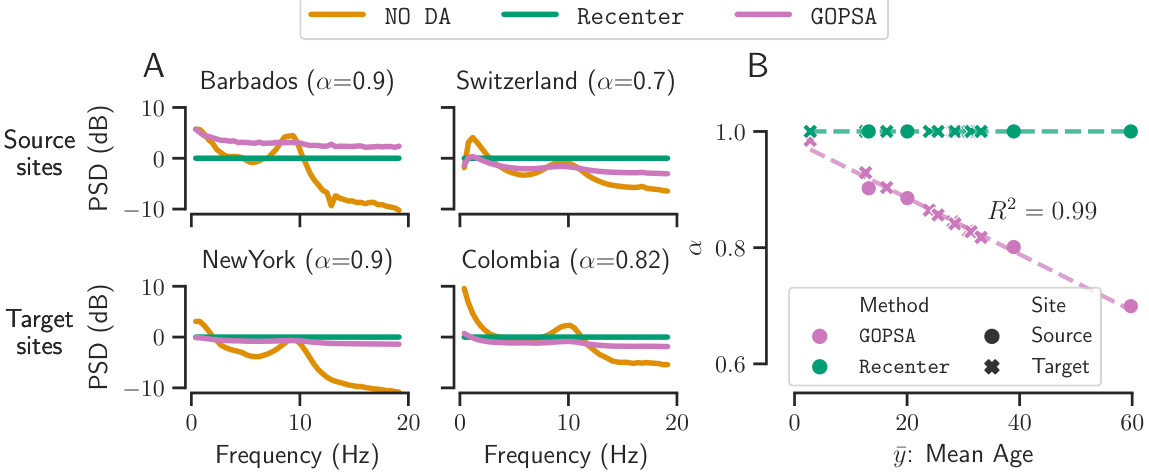
This figure displays a model inspection comparing GOPSA against No DA and Re-center methods. Panel A shows the mean power spectral densities (PSDs) across sensors for four sites (two source, two target) using the three different methods. It demonstrates how GOPSA maintains relevant frequency information compared to No DA and Re-center, which show significant differences. Panel B illustrates the relationship between the alpha values learned by GOPSA and the mean age of the sites. It visually confirms the relationship and model interpretability of GOPSA’s re-centering.

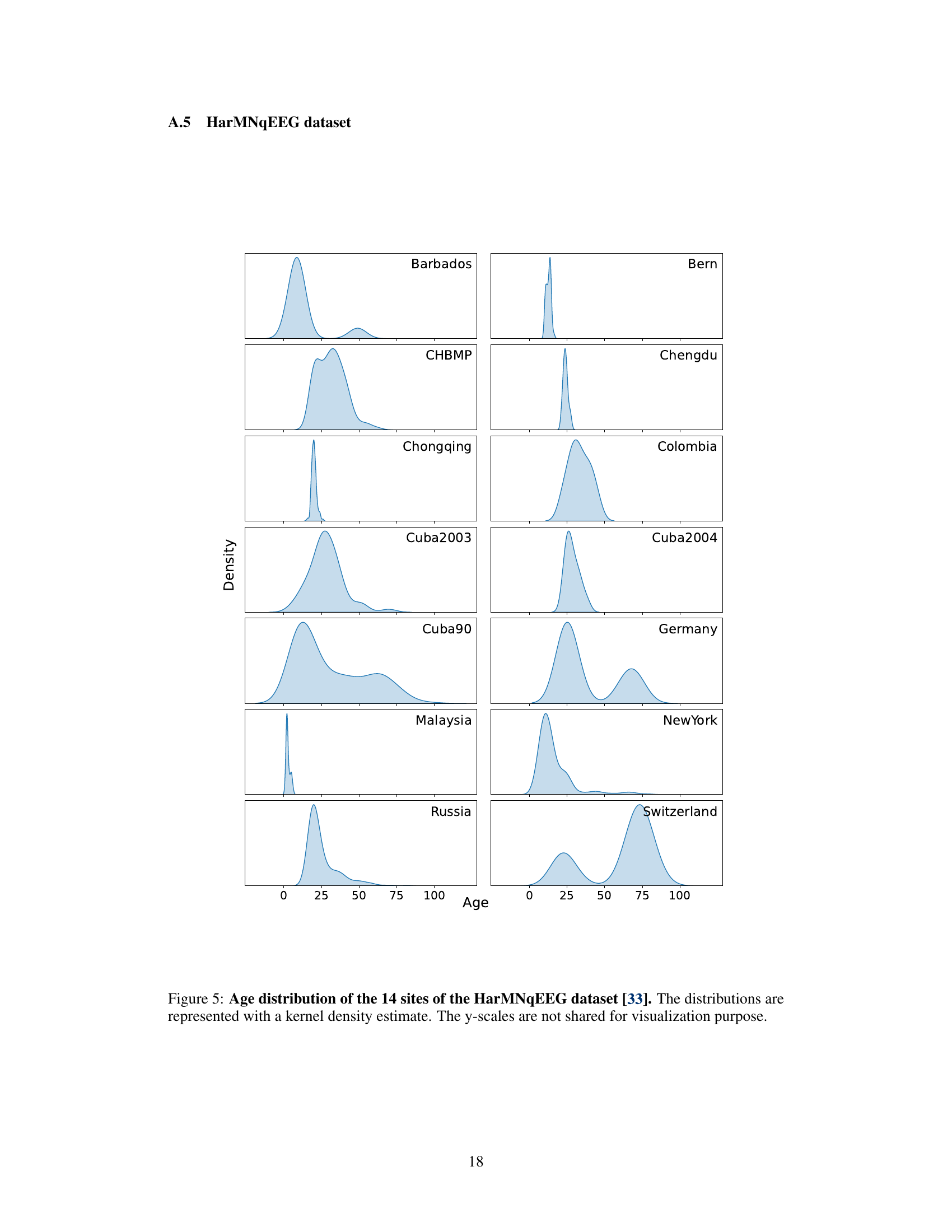
This figure shows the age distribution for each of the 14 sites in the HarMNqEEG dataset. Each site’s age distribution is represented as a kernel density estimate, allowing for visualization of the distribution’s shape and spread. The y-axis scales are not consistent across all sites for better visualization of individual distributions.

This figure displays the R-squared scores for different domain adaptation methods on simulated data with varying degrees of distribution shifts in both input features (X) and the target variable (y). Three scenarios are presented: (A) shift in X only, (B) shift in y only, and (C) joint shift in X and y. The performance of each method is evaluated across 5 source domains and 1 target domain, with 100 repetitions for each scenario. The results demonstrate the effectiveness of GOPSA in handling joint shifts and show its superiority to other methods in scenarios involving either a shift in X or y or a combination of both.

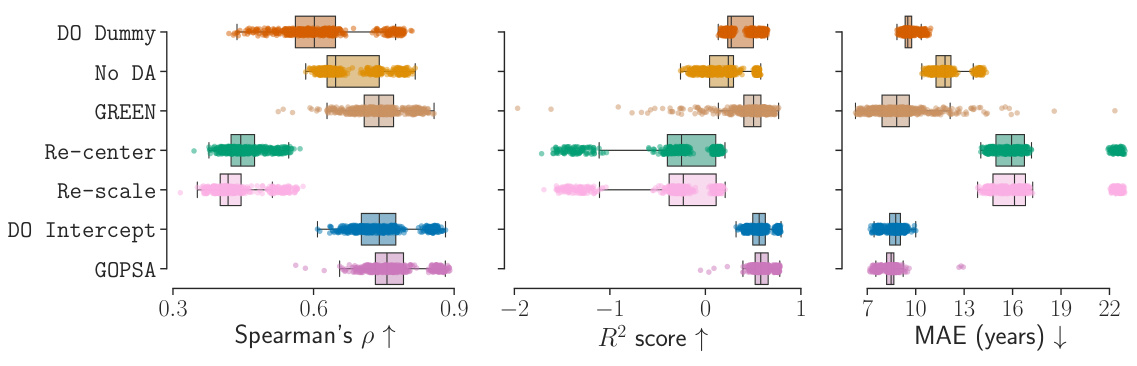
This figure displays the performance comparison of different domain adaptation methods (GOPSA, DO Dummy, No DA, GREEN, Re-center, Re-scale, DO Intercept) on the HarMNqEEG dataset. The performance is evaluated using three metrics: Spearman’s ρ (correlation), R² score (coefficient of determination), and MAE (mean absolute error). The results are normalized and presented as boxplots, showing the distribution of performance across multiple source-target site combinations. Part (A) shows the overall comparison of all methods, while Part (B) focuses on the pairwise comparison between GOPSA and DO Intercept, highlighting statistically significant differences.

This figure displays the R-squared scores for several methods on simulated data with varying degrees of shifts in the data (X) and the outcome variable (y). The experiment compares the performance of GOPSA against other methods (DO Dummy, No DA, GREEN, Re-center, Re-scale, DO Intercept) across three scenarios: shift in X only, shift in y only, and joint shifts in both X and y. The x-axis represents the magnitude of the shift (ξ), while the y-axis represents the R-squared scores. Each bar represents the average performance with error bars. The results show that GOPSA demonstrates the best performance overall, especially when both X and y are shifted, highlighting its effectiveness in handling predictive shifts in multi-source domain adaptation on the Riemannian manifold.

This figure displays the R-squared scores for various methods on simulated data, illustrating the impact of shifts in the data (X) and/or the outcome variable (y). Three scenarios are shown: shifts in X only, shifts in y only, and joint shifts in both X and y. The intensity of the shift is controlled by ξ. Each bar represents the average R-squared score across 100 simulations, comparing GOPSA to multiple baseline methods. The results showcase GOPSA’s superiority in handling shifts, especially joint shifts in X and y.

This figure compares the performance of different domain adaptation methods (DO Dummy, No DA, GREEN, Re-center, Re-scale, DO Intercept, and GOPSA) on simulated EEG data with varying levels of distribution shifts. The shifts are controlled by the parameter ξ, affecting either the covariance matrices (X), the variances of the underlying signal (y), or both simultaneously. The results are shown in terms of R2 scores, with higher scores indicating better performance. The figure demonstrates GOPSA’s effectiveness in handling various types and levels of distribution shifts in data and labels.

Full paper

#