Non-Asymptotic Uncertainty Quantification in High-Dimensional Learning

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on uncertainty quantification in high-dimensional settings and deep learning. It provides a novel, data-driven method that addresses limitations of existing techniques, offering more reliable confidence intervals and broader applicability to various models. This work opens new avenues for improving the reliability and trustworthiness of high-dimensional learning models, particularly in safety-critical applications, and bridges the gap between established theory and practical applications. The method extends beyond sparse regression to data-driven predictors like neural networks, improving the reliability of deep learning.

Visual Insights

#

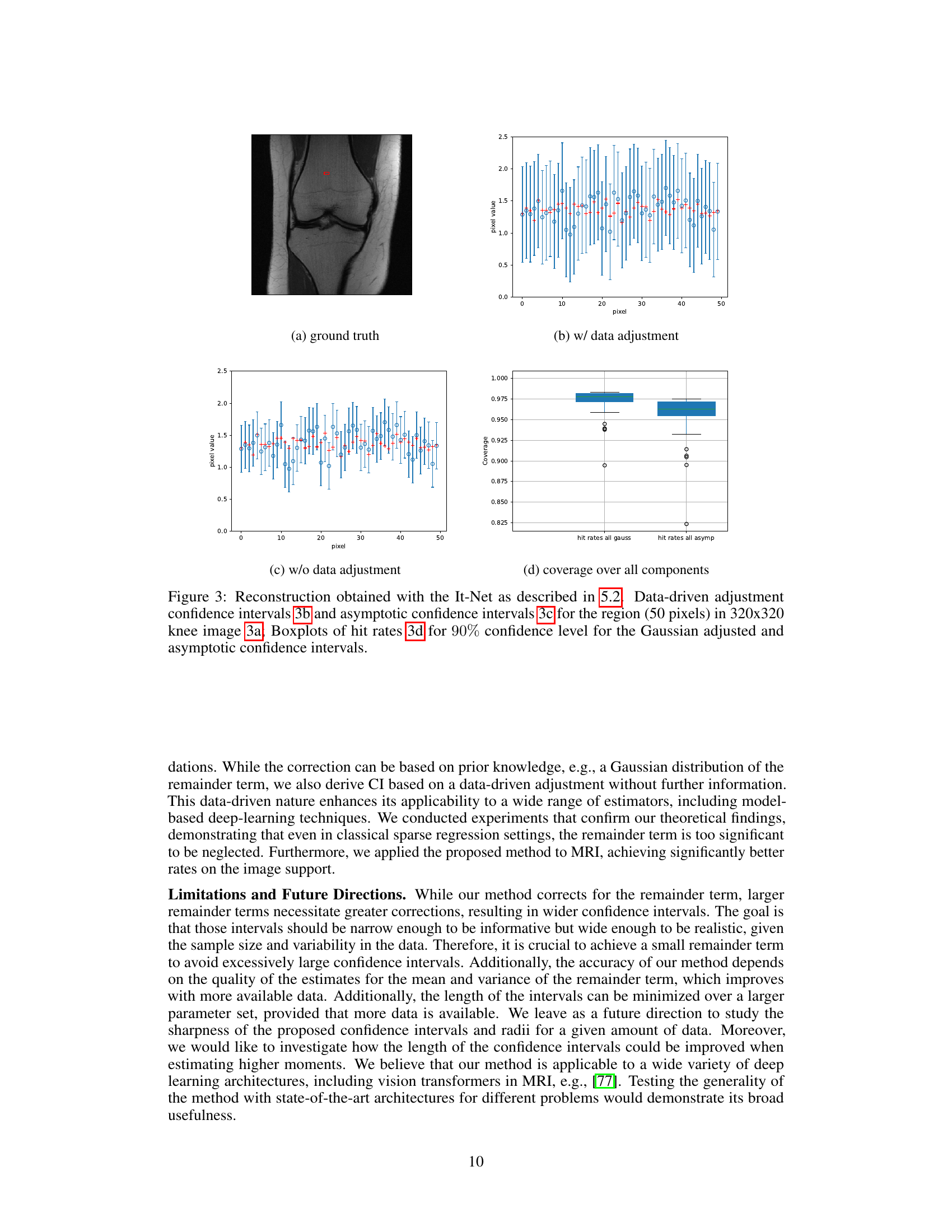
This figure illustrates the confidence interval correction methods proposed in the paper. It compares the construction of confidence intervals (CIs) using standard debiased techniques, a Gaussian adjustment, and a data-driven adjustment. The figure visually demonstrates the improved coverage achieved by the proposed methods, particularly in capturing entries not covered by the asymptotic CIs. The results are shown both for all components and for the support (non-zero entries) of the vectors.

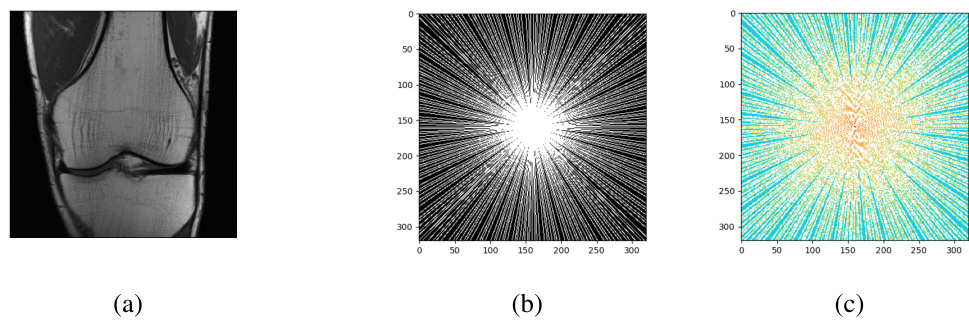
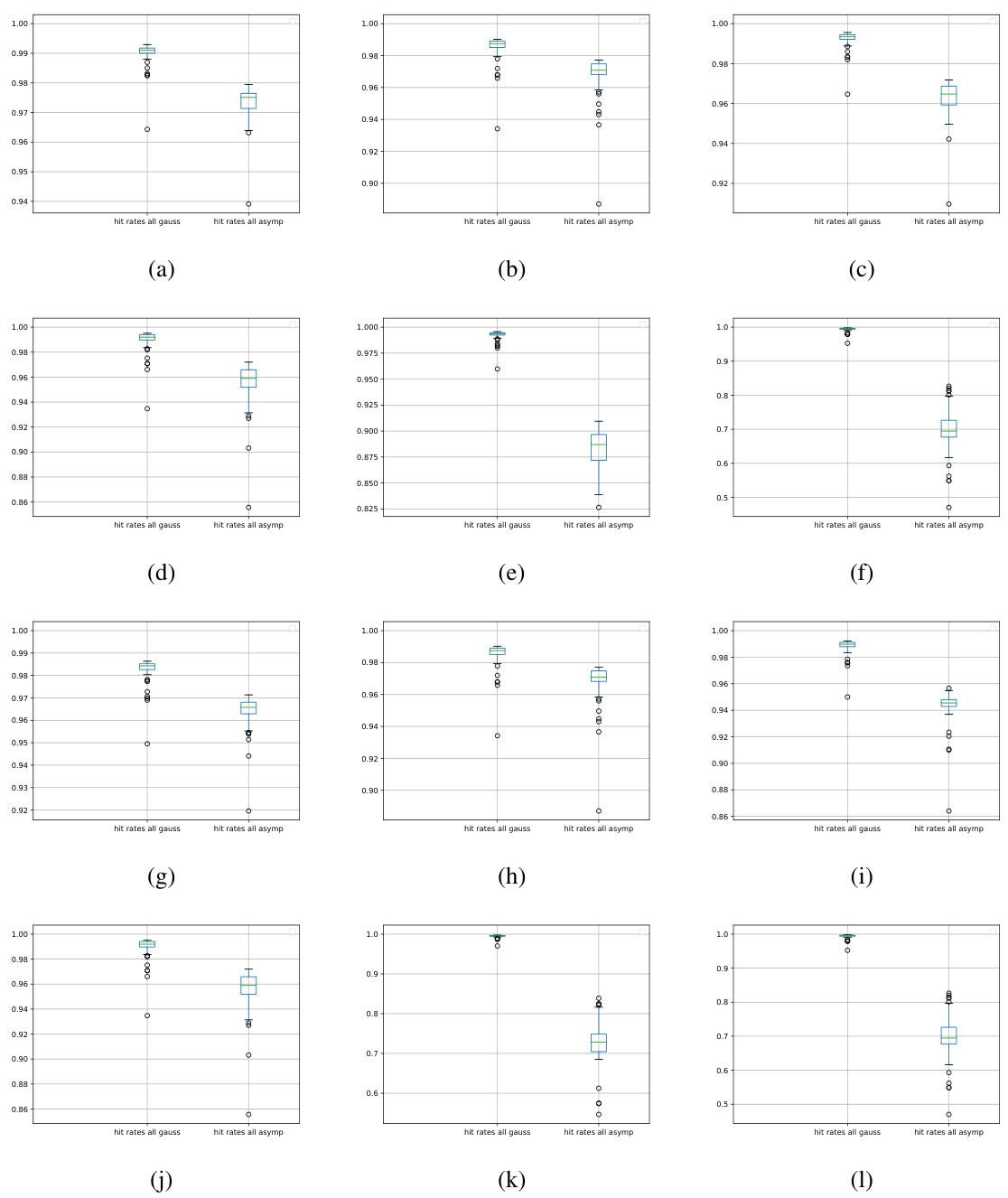
This table presents the results of experiments on sparse regression using both Gaussian and Fourier measurement matrices. It compares the performance of different methods for uncertainty quantification. The table shows the settings used (feature dimension, undersampling, sparsity, relative noise) and the results obtained by various methods, including the asymptotic method, Gaussian adjustment, and the data-driven adjustment proposed in the paper. The metrics used for evaluating performance are the ratio of remainder to Gaussian terms (both l2 and l-infinity norms), average radius for asymptotic and adjusted confidence intervals, and finally the hit rates for both overall and on support (non-zero pixels).

In-depth insights

#

Non-Asymptotic UQ

#

The concept of “Non-Asymptotic Uncertainty Quantification (UQ)” signifies a crucial advancement in statistical inference, especially within high-dimensional settings. Traditional asymptotic UQ methods often rely on assumptions that become unreliable with finite datasets, common in real-world applications. Non-asymptotic UQ directly addresses this limitation by providing uncertainty quantification guarantees without relying on asymptotic limits. This is achieved by explicitly incorporating and quantifying the impact of bias terms, often neglected in asymptotic frameworks, which becomes critical when dealing with finite-dimensional data. This approach leads to more reliable confidence intervals and uncertainty estimates. The data-driven nature of non-asymptotic UQ, estimating bias terms from the training data, enhances its practical applicability and robustness in various scenarios, especially model-based deep learning where asymptotic analysis can be difficult to apply. A key advantage is its applicability across different predictor types, from classical methods like LASSO to complex machine learning models, improving overall reliability and confidence in model predictions.

Debiased LASSO UQ

#

Debiased LASSO UQ addresses the challenge of uncertainty quantification (UQ) in high-dimensional regression. Standard LASSO, while effective for variable selection, introduces bias, hindering precise uncertainty estimation. The debiasing technique modifies the LASSO estimator to decompose the error into Gaussian and bias components. Asymptotic confidence intervals, based on the Gaussian component, are then constructed. However, the finite-sample bias often significantly impacts the accuracy of asymptotic UQ. This is where the proposed data-driven approach excels by explicitly modeling and estimating the bias, which leads to more reliable non-asymptotic confidence intervals that better reflect uncertainty in real-world data settings. Furthermore, this method extends to complex models beyond sparse regression, proving particularly useful for model-based deep learning techniques. The data-driven adjustment of confidence intervals effectively addresses the limitations of existing asymptotic methods, paving the way for improved reliability in high-stakes applications where accurate uncertainty quantification is critical.

Data-Driven Approach

#

A data-driven approach in this context likely refers to a methodology that leverages empirical evidence and real-world data to inform and improve a model or technique. This contrasts with traditional methods that primarily rely on theoretical assumptions or simulations. A key advantage is its ability to handle complex real-world scenarios where simplifying assumptions may not hold. The approach likely involves using data to estimate model parameters, assess performance, and guide refinements. This data-driven nature allows for better adaptation to specific datasets and problem domains, enhancing accuracy and reliability. The process may involve iterative steps of data collection, analysis, model building, and evaluation. The emphasis would be on the use of data to inform the development and tuning of models, rather than purely theoretical or heuristic methods. This approach is particularly valuable in high-dimensional settings or those with complex relationships where traditional methods might be less effective. However, challenges could include potential biases in the data, the need for large datasets, and the computational demands of processing large datasets. The success of a data-driven approach also hinges on careful design and interpretation to avoid overfitting and bias.

Gaussian Remainders

#

The concept of “Gaussian Remainders” in high-dimensional statistics is crucial for refining uncertainty quantification. It addresses the limitations of asymptotic confidence intervals by acknowledging that the remainder term in the error decomposition of debiased estimators doesn’t always vanish in finite-sample scenarios. The core idea is to model this remainder term, often non-negligible, using a Gaussian distribution. This approximation allows for a more accurate calculation of confidence intervals. While convenient, this Gaussian assumption needs careful consideration and validation, potentially requiring empirical verification to ensure its appropriateness for the specific data and model used. The validity of the Gaussian assumption significantly impacts the accuracy and reliability of the resulting confidence intervals, especially in high-stakes applications where precise uncertainty estimates are critical. Furthermore, the efficacy of this approach hinges on the ability to accurately estimate the mean and variance of the Gaussian remainder; consequently, sufficient data and appropriate estimation techniques are essential for successful implementation.

Future Directions

#

The paper’s “Future Directions” section would ideally delve into several key areas. Firstly, it should address the limitations of the current approach, specifically focusing on improving the estimation of the remainder term in non-asymptotic regimes. More refined methods for this estimation, perhaps incorporating advanced statistical techniques or machine learning models, could significantly enhance the accuracy and precision of the confidence intervals. Secondly, extending the theoretical framework to encompass a broader range of high-dimensional learning models beyond the LASSO and neural networks is crucial. This could involve exploring applications in other model classes, and potentially adapting the methodology to different types of data and loss functions. Thirdly, future work might focus on developing adaptive methods that automatically determine optimal parameters, thereby enhancing the practical usability of the uncertainty quantification techniques. Finally, investigating the effects of model complexity and data size on the accuracy of the confidence intervals would further solidify the theoretical understanding and guide the development of more robust and reliable methods. Thorough investigation of these areas will significantly increase the impact and relevance of the presented work.

More visual insights

#

More on figures

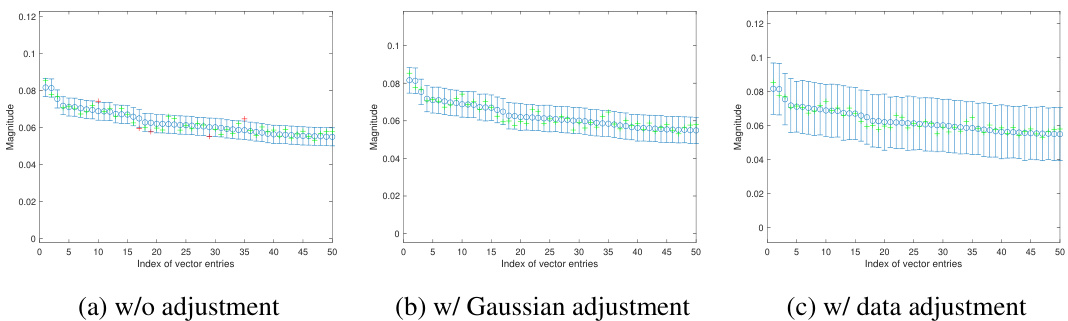
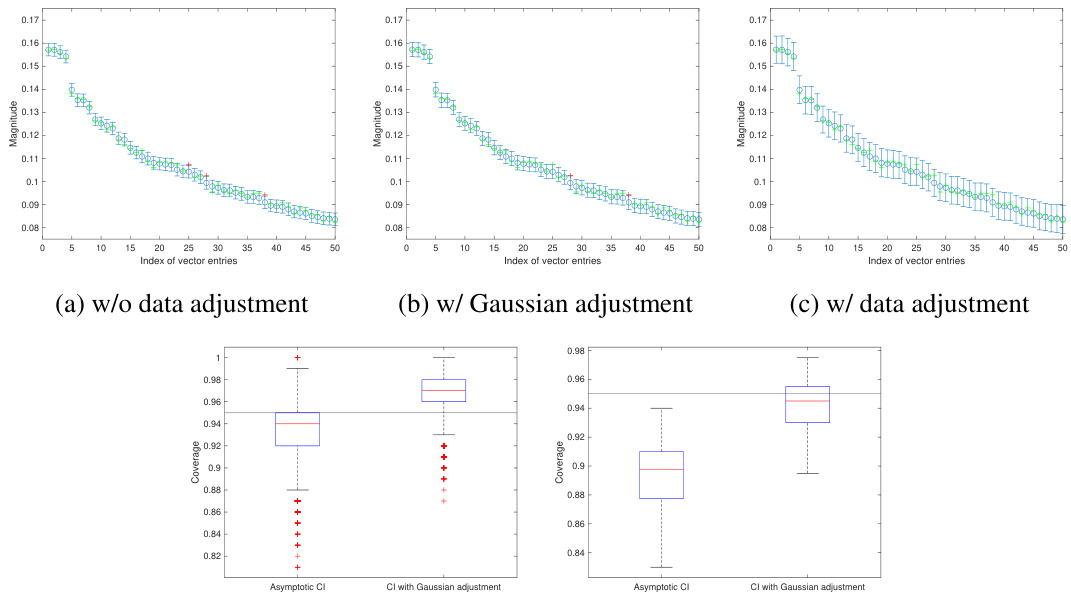
This figure illustrates the confidence interval correction methods. It compares standard debiased techniques to the proposed method, showing how the new method improves coverage, particularly on the support (non-zero entries). The plots visualize the construction of confidence intervals and show the effect of the proposed adjustments (Gaussian and data-driven) on the coverage rate for sparse regression problems solved using the LASSO.

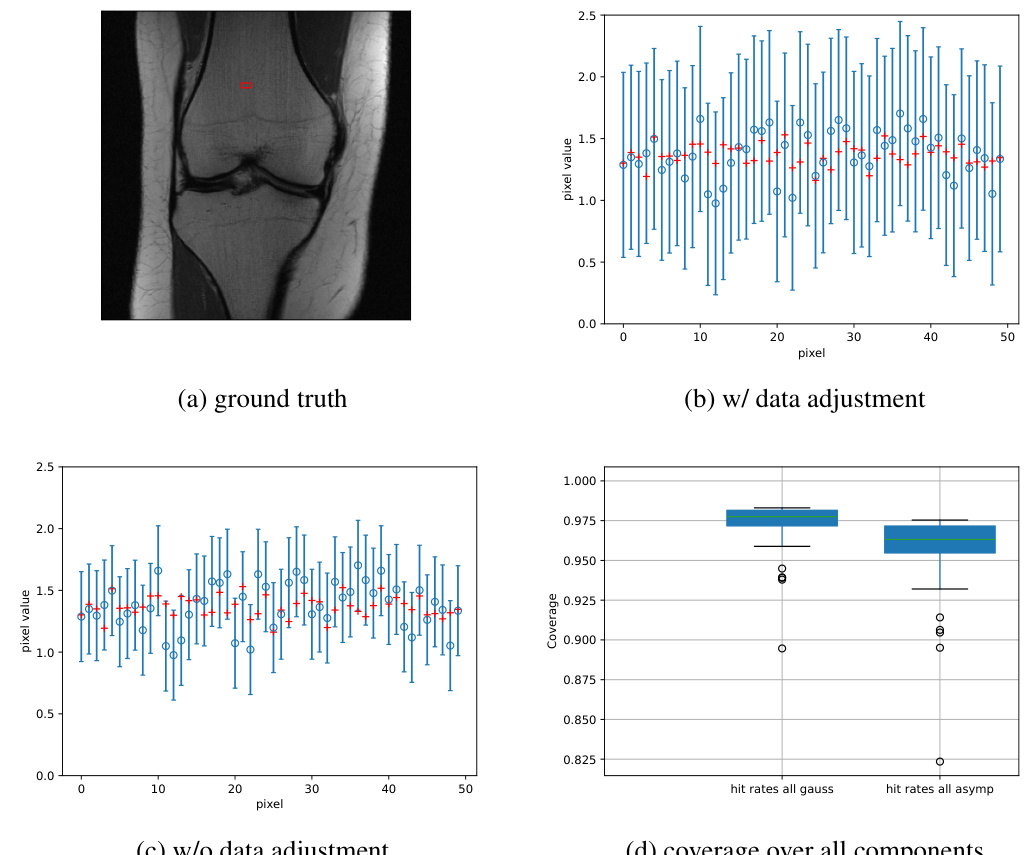
This figure illustrates the effectiveness of the proposed method for constructing confidence intervals (CIs) by comparing it to standard debiased techniques. It shows that the proposed method provides more accurate CIs, especially on the support of the sparse regression problem, even in finite-sample scenarios, and corrects for the bias term.

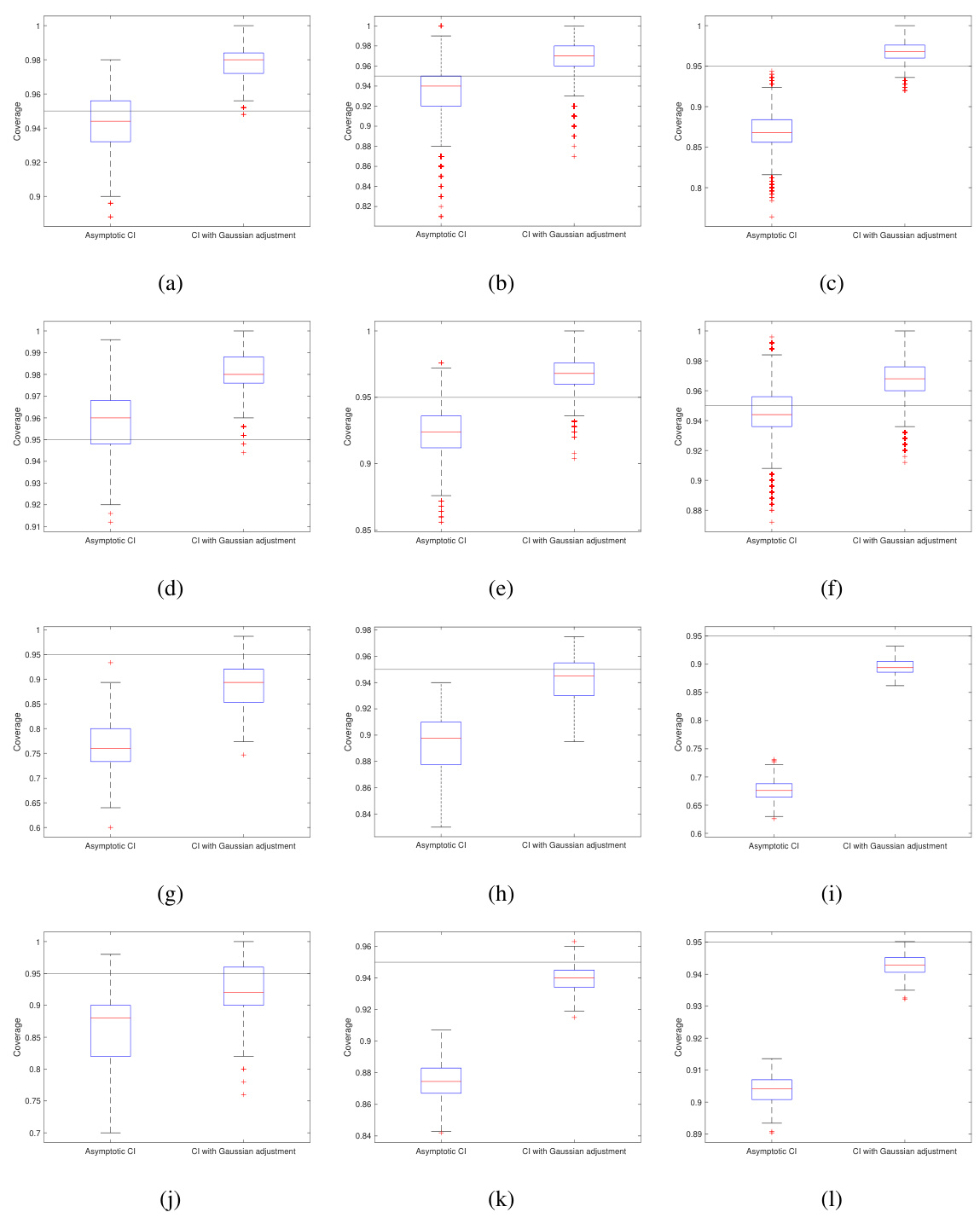
This figure illustrates the construction of confidence intervals (CIs) using three different methods: standard debiased techniques, Gaussian adjustment, and data-driven adjustment. It compares the performance of these methods in capturing true values, particularly focusing on the coverage on the support (non-zero values). The figure highlights how the proposed data-driven approach leads to significantly improved coverage, correcting for issues with the asymptotic CI method that are especially problematic in real-world finite-sample scenarios.

The figure illustrates the confidence interval correction methods. It compares the construction of confidence intervals (CIs) using standard debiased techniques, Gaussian adjustment, and data adjustment methods. The plots show the effectiveness of the proposed methods in capturing the true values and avoiding overestimation of certainty. Key features illustrated include the impact of bias correction on CI width and coverage, particularly for sparse regression problems.

This figure illustrates the confidence interval correction methods. It compares standard debiased techniques with the proposed methods, showing how the proposed methods improve coverage, particularly for non-captured entries. The plots visualize coverage across all components and only on the support (non-zero entries), comparing asymptotic and non-asymptotic confidence intervals. A sparse regression problem is used to generate the data.

This figure illustrates the construction of confidence intervals using three different methods: asymptotic, Gaussian adjustment, and data-driven adjustment. It shows how each method handles the construction of confidence intervals for a single feature vector in a sparse regression setting, highlighting the impact of accounting for the remainder term in non-asymptotic regimes. The plot shows that the data-driven adjustment method provides the most accurate confidence intervals.

This figure illustrates the proposed method for correcting confidence intervals in high-dimensional regression. It compares standard debiased techniques with the proposed method, showing how the proposed method improves the coverage of confidence intervals, especially on the support (non-zero entries). Subfigures (a), (b), and (c) show individual examples, while (d) and (e) show boxplots summarizing the results.

This figure illustrates the confidence interval correction methods proposed in the paper. It compares standard debiased techniques to the proposed method, highlighting the impact of data and Gaussian adjustments on coverage. The plots showcase the construction of confidence intervals (CIs), showing how the proposed method addresses the limitations of asymptotic CIs by improving coverage, especially on the support (non-zero elements).

More on tables

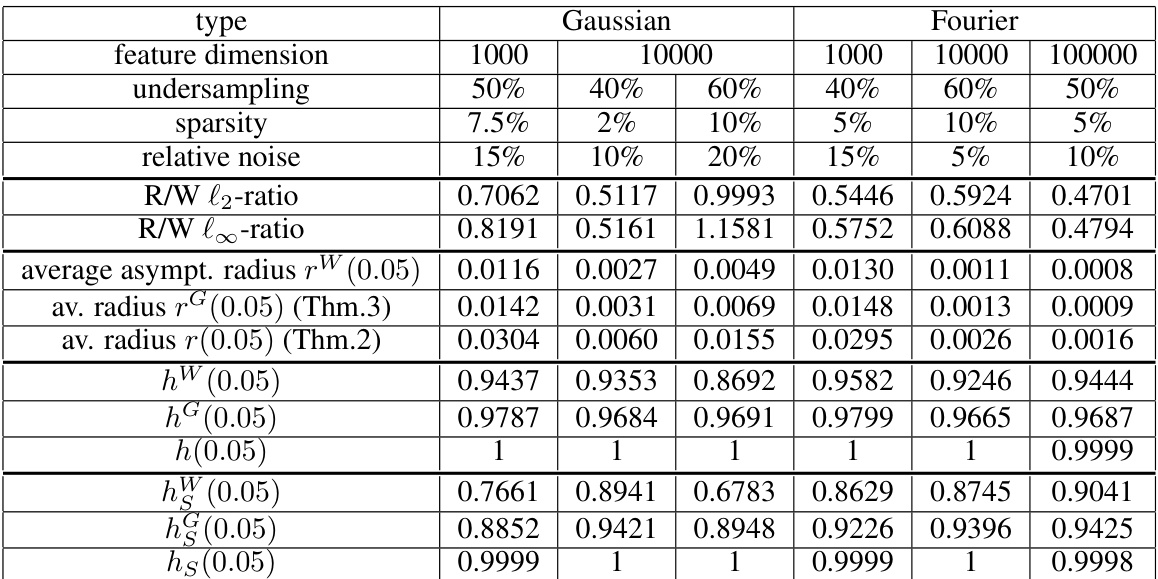
This table presents the results of experiments conducted for sparse regression using both Gaussian and Fourier matrices. Each experiment uses 500 data points for estimation and 250 for evaluation. The table shows various metrics to assess the performance of different methods, including hit rates and radii calculations. These metrics are compared for asymptotic, Gaussian adjusted, and data driven adjusted confidence intervals, providing insights into the accuracy and efficiency of each method under different conditions.

This table presents the results of experiments conducted for sparse regression using both Gaussian and Fourier matrices as measurement matrices. The table shows the impact of different experimental settings (dimensionality, undersampling rate, sparsity, noise level) on the performance of the debiased Lasso and the proposed methods for uncertainty quantification. It compares several metrics such as the ratio of remainder term to Gaussian term (both L2 and L-infinity norms), the average radius of asymptotic and adjusted confidence intervals, and various hit rates (coverage rates of the confidence intervals, both overall and on the support). The results demonstrate that in a high-dimensional setting the bias term is often too significant to disregard.

Full paper

#