Doob's Lagrangian: A Sample-Efficient Variational Approach to Transition Path Sampling

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on rare event sampling, particularly in molecular dynamics. It offers a significant advancement over existing methods by improving efficiency and reducing computational costs. This work opens doors for future research focusing on optimizing the model’s expressiveness further and extending it to handle even more complex systems.

Visual Insights

#

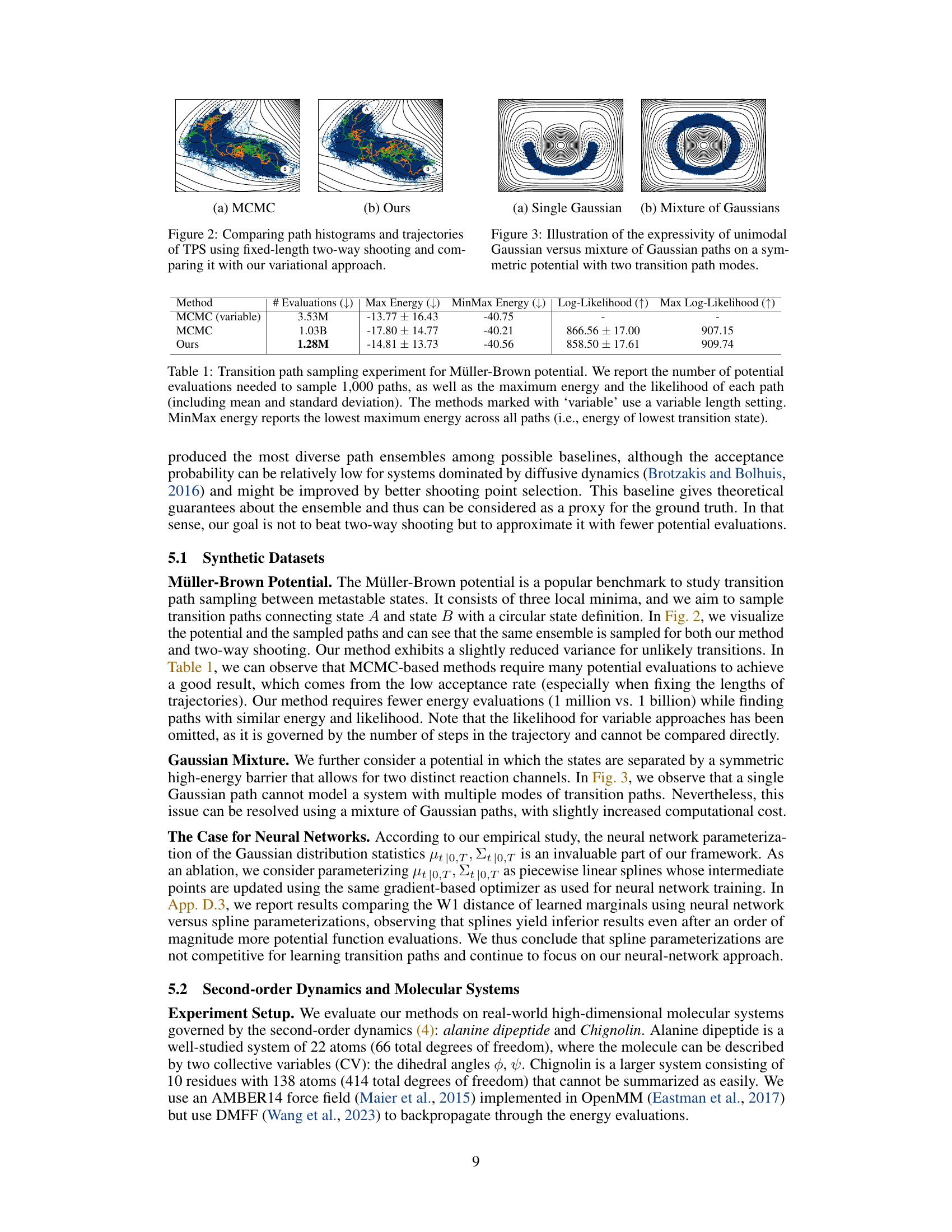
This figure compares the results of transition path sampling using two different methods: Markov Chain Monte Carlo (MCMC) with fixed-length two-way shooting and the proposed variational approach. The left panel (a) shows the results from the MCMC method, while the right panel (b) shows the results from the proposed method. Both panels show histograms and representative trajectories (paths) generated by the respective methods. The figure visually demonstrates that the variational method can achieve comparable performance to the MCMC method, especially in terms of sampling trajectories that successfully transition between the initial and final states.

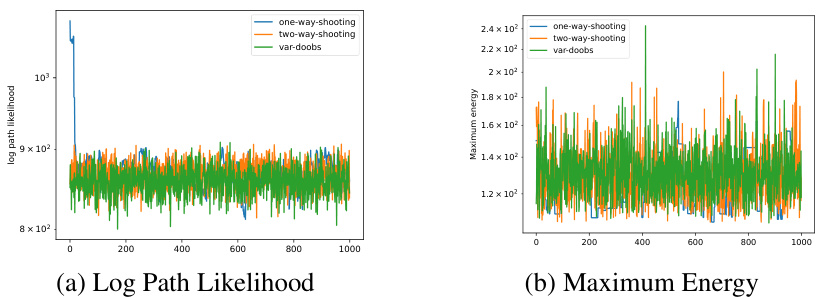
This table presents a comparison of the performance of different transition path sampling methods on the Müller-Brown potential. The metrics used are the number of potential energy evaluations required, the maximum energy along sampled paths, the minimum of maximum energies across all paths, the average log-likelihood of paths, and the maximum log-likelihood.

In-depth insights

#

Doob’s Lagrangian

#

The conceptualization of a ‘Doob’s Lagrangian’ within the context of transition path sampling presents a novel and powerful approach. By framing the problem of conditioning stochastic processes as a variational optimization problem, the authors elegantly leverage Doob’s h-transform. This reformulation offers significant computational advantages over traditional methods like importance sampling. The use of a Lagrangian allows for an intuitive description of the system’s dynamics and its constraints, leading to a more efficient and principled method for determining feasible transition paths. The central idea involves minimizing an action functional, a direct consequence of the underlying Brownian motion dynamics, leading to an optimal control formulation. This approach promises sample efficiency and avoids expensive trajectory simulations inherent in existing methods, particularly benefiting rare event studies. The successful application to molecular simulations and protein folding problems further supports the potential of this novel ‘Doob’s Lagrangian’ framework.

Variational TPS

#

Variational Transition Path Sampling (TPS) offers a novel approach to tackle the computational challenges inherent in traditional TPS methods. By framing TPS as a variational inference problem, it significantly reduces the search space by directly optimizing over a parameterized family of probability distributions, rather than relying on expensive Monte Carlo sampling of trajectories. This variational perspective allows for the incorporation of prior knowledge and boundary conditions, further enhancing efficiency. Simulation-free training eliminates the need for computationally expensive trajectory simulations, making it particularly advantageous for systems with high dimensionality and rare events. The use of neural networks for parameterization allows for flexibility and scalability, offering the potential for application to complex real-world problems. Sample efficiency is a key benefit, drastically improving upon the computational cost of conventional methods. However, careful consideration of parameterization choices is necessary for accurate representation and to avoid oversimplification of complex transition path dynamics. The expressiveness of the variational family also needs careful management to balance tractability and accuracy.

Gaussian Paths

#

The concept of Gaussian paths in the context of transition path sampling offers a powerful and efficient approach to approximate the complex, high-dimensional probability distributions of trajectories. By parameterizing the paths using Gaussian distributions, the method simplifies the problem significantly, making it computationally tractable. The Gaussian assumption provides a balance between model expressiveness and analytical tractability. The choice of Gaussian distributions is particularly advantageous because of their mathematical properties, which enable efficient sampling and optimization. This contrasts sharply with methods relying on brute-force sampling or less efficient importance sampling. The use of neural networks to further parameterize the mean and covariance of the Gaussian paths allows for learning complex relationships between the initial and final states, leading to accurate approximations. Furthermore, the ability to directly sample trajectories from the learned Gaussian distribution avoids the need for time-consuming simulations, significantly improving the sample efficiency of the method. While the Gaussian assumption may not perfectly capture the true path distribution in all scenarios, its efficiency and accuracy demonstrate that it is a valuable contribution to the transition path sampling field.

Sample Efficiency

#

The concept of sample efficiency in the context of transition path sampling is crucial. The paper highlights the computational cost of traditional methods like Monte Carlo, which necessitate simulating numerous trajectories to accurately estimate rare event probabilities. The proposed variational approach significantly enhances sample efficiency by avoiding expensive trajectory simulations. Instead, it directly optimizes a variational distribution over trajectories, effectively reducing the search space and making every sampled point more valuable. This simulation-free training objective is a key aspect of the method’s efficiency. By design, the approach ensures that the optimized trajectories satisfy boundary conditions, which further improves sample efficiency by focusing the optimization on relevant trajectory space, thus minimizing wasteful exploration. The results demonstrate the sample efficiency on real-world applications, showcasing its practicality and potential to accelerate rare event sampling in complex systems like protein folding.

Future Directions

#

The paper’s ‘Future Directions’ section would ideally explore extending the variational approach to handle more complex systems. Addressing limitations such as the rigid boundary conditions and the Gaussian path parameterization would be crucial, perhaps through incorporating more flexible distributions or incorporating alternative methods. Investigating the scalability of the proposed method for significantly larger systems, especially those found in real-world molecular simulations, is vital. A direct comparison with alternative state-of-the-art transition path sampling techniques on a broader range of challenging problems would further strengthen the paper’s findings. Finally, exploring the method’s application to different stochastic processes beyond Brownian motion would open exciting avenues of research. The potential for integration with other machine learning approaches to further enhance sampling efficiency or improve the accuracy of rare event estimation should also be considered.

More visual insights

#

More on figures

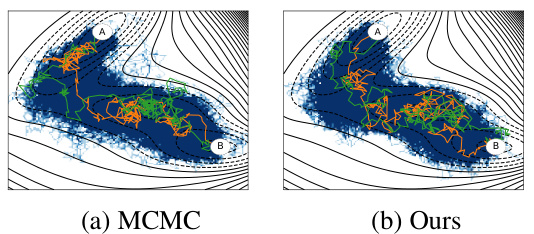
This figure compares the performance of unimodal Gaussian and mixture of Gaussian paths for modeling transition paths on a symmetric double-well potential. The left panel (a) shows the results obtained using a single Gaussian, highlighting its limitations in capturing the two distinct transition pathways. The right panel (b) demonstrates the improved expressiveness of using a mixture of Gaussians, effectively representing both pathways and showcasing its ability to handle more complex transition path scenarios.

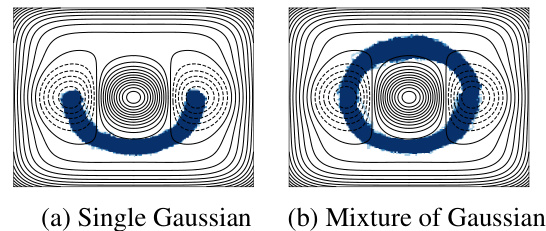
This figure shows a transition path for the protein Chignolin. The top panel displays the 3D structure of the protein at various points along the trajectory, illustrating its folding process. The bottom panel shows a plot of the potential energy (U(x)) of the protein as a function of time (fs), clearly indicating a high energy barrier around 460 fs before the protein reaches the final folded state at 1000 fs.

This figure compares the results of transition path sampling using two different methods: a traditional fixed-length two-way shooting method and the novel variational approach proposed in the paper. The left panel shows histograms of the paths generated by both methods, while the right panel displays example trajectories. The figure visually demonstrates that the variational approach produces a similar distribution of paths with fewer computational evaluations.

This figure compares the path histograms and trajectories generated by the proposed variational approach with those obtained using fixed-length two-way shooting. The left panel shows the histogram of paths, while the right panel displays example trajectories. This comparison highlights the efficiency and accuracy of the variational approach in capturing the conditional distribution over transition paths.

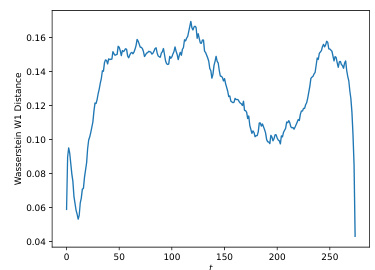
The figure compares three different parameterization techniques for the mean and covariance matrix of a Gaussian distribution used to approximate transition paths: linear spline, cubic spline, and a neural network. The Wasserstein W1 distance is used to measure the difference between the learned marginal distribution and the marginal distribution obtained from a fixed-length two-way shooting method (considered the ground truth). The plot shows that the neural network provides the best approximation, with the cubic spline performing better than the linear spline. This highlights the advantage of using neural networks for increased expressivity and accuracy in capturing complex probability distributions of transition paths.

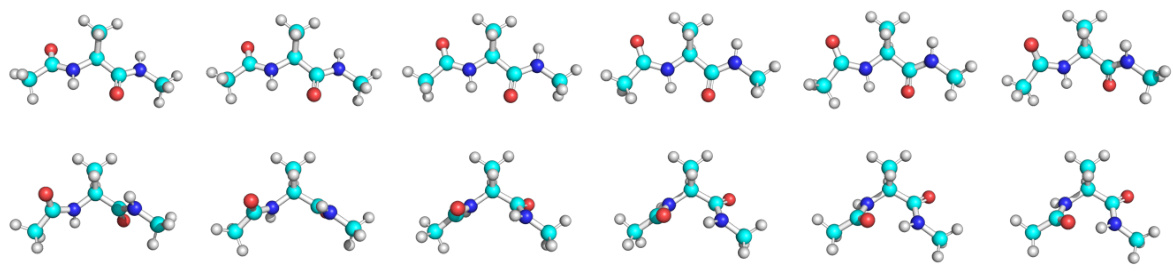
This figure visualizes a transition path for the alanine dipeptide molecule. It shows a sequence of molecular conformations along a transition path, highlighting the changes in the molecule’s structure as it transitions between states. The figure is part of a study using a novel variational approach to transition path sampling, and helps illustrate the ability of the method to generate plausible transition paths.

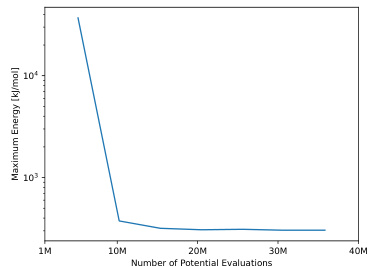
This figure shows the maximum energy of the sampled paths during training as a function of the number of potential energy evaluations. The plot demonstrates that as training progresses (more potential energy evaluations are performed), the maximum energy along the generated paths decreases. This indicates that the model is learning to generate more realistic and likely transition paths with lower energy barriers. The decreasing trend suggests improved sampling of low-energy paths.

This figure shows the training loss curves for different model configurations. The models use either Cartesian or internal coordinates, and with either a single Gaussian or a mixture of two Gaussians to represent the probability distribution of the transition paths. The plot shows that using a mixture of Gaussians can help decrease the overall loss, but all the variations converge to a similar loss value. This observation suggests that while mixture models show some benefit, there may be a limit to how much they improve the model’s performance.

Full paper

#