EigenVI: score-based variational inference with orthogonal function expansions

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is significant for researchers in Bayesian inference and machine learning because it introduces a novel, efficient approach for black-box variational inference. EigenVI offers a computationally advantageous alternative to traditional gradient-based methods, addressing challenges in optimization and hyperparameter tuning. Its flexibility in handling various probability distributions and its avoidance of iterative optimization opens exciting avenues for research, including scalable probabilistic modeling and complex posterior approximations.

Visual Insights

#

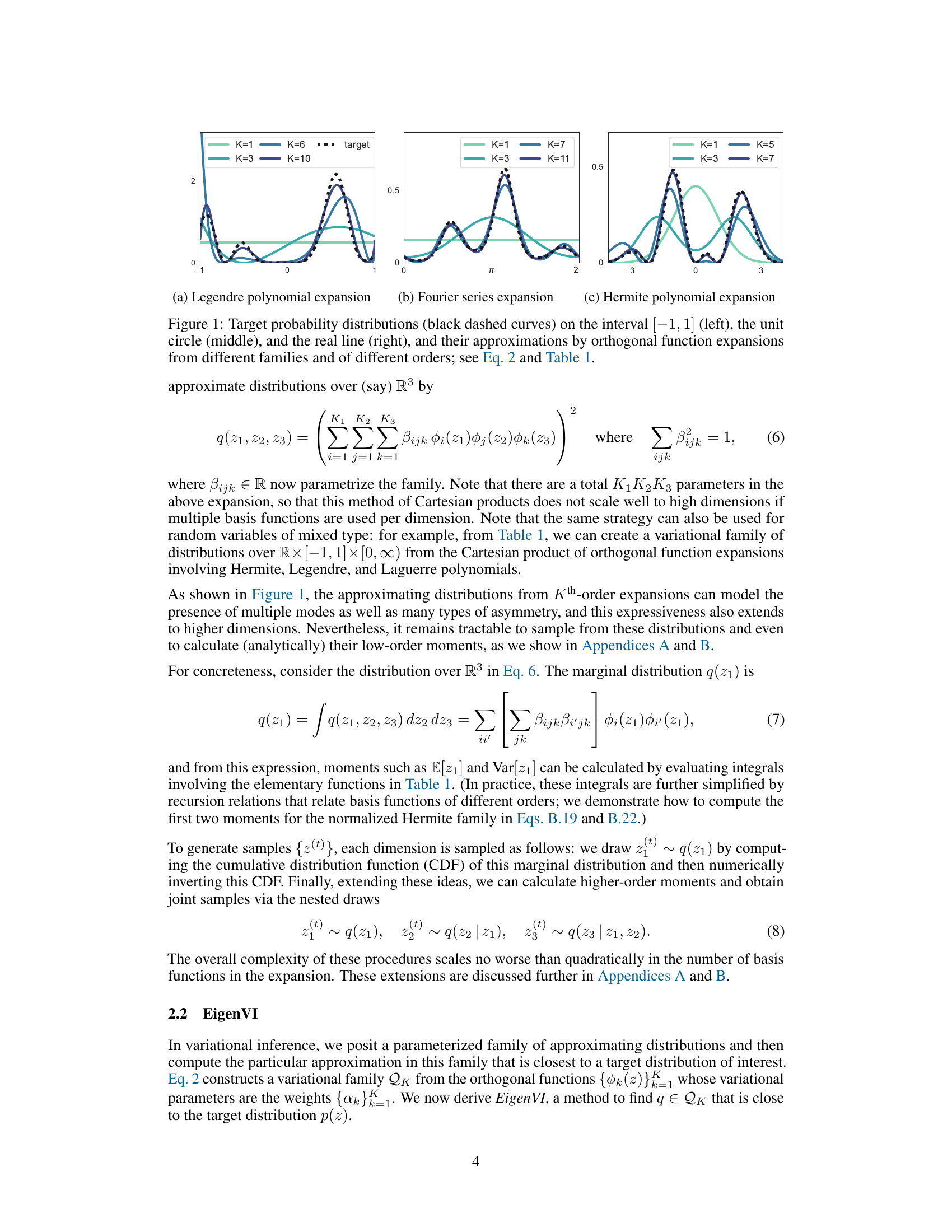
This figure shows how various probability distributions can be approximated using orthogonal function expansions. It demonstrates the flexibility of this approach by showing examples on three different types of support: the interval [-1,1], the unit circle, and the real line. Each example shows a target distribution (black dashed curve) and its approximations using different numbers of basis functions from different families (Legendre polynomials, Fourier series, and Hermite polynomials). The approximations become more accurate as the number of basis functions increases.

This table presents examples of orthogonal function expansions in one dimension. It shows four different families of orthogonal functions (Legendre polynomials, Fourier basis, weighted Laguerre polynomials, and weighted Hermite polynomials), each suitable for approximating functions over a specific support ([-1,1], the unit circle S¹, [0, ∞), and R, respectively). The table lists the support for each function family and their corresponding basis functions.

In-depth insights

#

EigenVI: Score-Matching

#

EigenVI leverages score-matching, a technique that bypasses direct density estimation, to perform black-box variational inference (BBVI). Instead of minimizing the Kullback-Leibler (KL) divergence, EigenVI directly matches the score functions (gradients of the log-densities) of the variational approximation and the target distribution. This avoids the need for iterative gradient-based optimization, a major advantage over traditional BBVI methods that often struggle with learning rates and convergence. EigenVI achieves score-matching by formulating the problem as a minimum eigenvalue problem, thus offering a closed-form solution and improved computational efficiency. The use of orthogonal function expansions allows EigenVI to model complex distributions with flexibility, going beyond the limitations of Gaussian approximations inherent in many score-matching approaches. The expressiveness of the method, along with its computational efficiency, makes EigenVI a promising alternative for BBVI in high dimensional spaces.

Orthogonal Expansions

#

Orthogonal expansions offer a powerful technique for approximating complex probability distributions within the framework of variational inference. The key advantage lies in their ability to systematically represent non-Gaussian features by combining simple basis functions. This contrasts with simpler Gaussian approximations, which often fail to capture the richness of real-world data. By constructing variational families from these expansions, the method facilitates efficient computation of low-order moments and sampling. This tractability is crucial for the success of the EigenVI algorithm, enabling it to avoid the iterative, gradient-based optimization that can plague other methods. The choice of basis functions (Hermite, Legendre, Fourier, etc.) is tailored to the support of the target distribution, allowing for flexibility in handling different data types and ensuring accurate representation of features. EigenVI’s reliance on score-matching further enhances the effectiveness of orthogonal expansions, as it directly targets the alignment of score functions between the approximation and the true distribution, leading to improved accuracy in the resulting inferences. The simplicity of the minimum eigenvalue problem that arises from this approach adds significant computational advantages over traditional gradient-based methods.

Eigenvalue Optimization

#

Eigenvalue optimization, in the context of a machine learning research paper, likely refers to a technique for finding the optimal parameters of a model by solving an eigenvalue problem. This approach offers several advantages. It avoids the iterative, gradient-based optimization often used in other machine learning methods, which can be sensitive to hyperparameters like learning rates and prone to getting stuck in local optima. Instead, an eigenvalue problem directly yields the optimal solution. The computational cost of this optimization is generally lower than iterative methods, especially when dealing with high-dimensional datasets. However, a critical point to consider is that the eigenvalue approach’s success depends heavily on the structure of the optimization problem, requiring the model and its objective function to be formulated appropriately to be cast as an eigenvalue problem. This method may not be universally applicable, limiting its use to specific classes of machine learning tasks and models.

BBVI Improvements

#

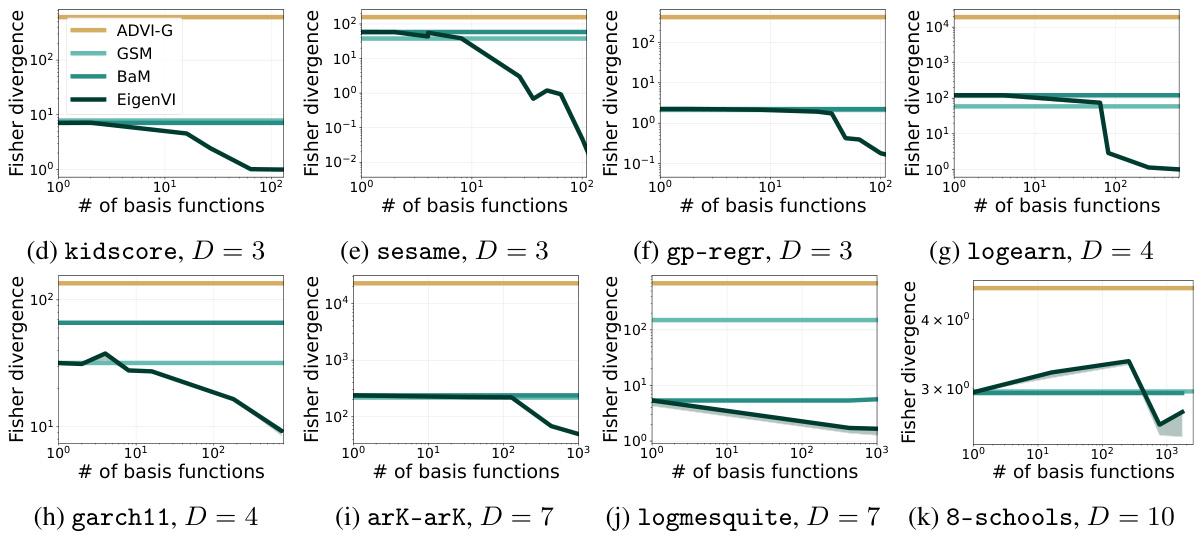
Black-box variational inference (BBVI) has seen significant advancements, addressing limitations in scalability and accuracy. EigenVI, for instance, offers a novel approach using orthogonal function expansions to create flexible variational families, effectively capturing complex target distributions. By minimizing Fisher divergence instead of KL divergence, EigenVI avoids the iterative gradient-based optimization typical in BBVI methods, thus sidestepping issues with learning rates and termination criteria. Another crucial improvement lies in the use of score-matching techniques, allowing for efficient computation of score functions. This approach shows promising results, particularly in the context of Bayesian hierarchical models, surpassing standard Gaussian BBVI in accuracy. Standardization of target distributions prior to applying EigenVI further enhances efficiency and accuracy, especially in higher dimensions. However, challenges remain regarding the sensitivity to hyperparameters like sample size and proposal distribution. Further research should focus on addressing these remaining challenges and exploring even more expressive variational families to expand the capabilities of BBVI.

Future Work Directions

#

Future research could explore several promising avenues. Extending EigenVI to higher dimensions is crucial, potentially by incorporating low-rank structures to mitigate the exponential scaling of the computational cost. Investigating alternative orthogonal function families, beyond Hermite polynomials, to better suit various data distributions and problem domains is also vital. Improving the efficiency of sampling from the high-dimensional variational distributions, perhaps via more advanced methods like Markov chain Monte Carlo or variance reduction techniques, would enhance practical applicability. Furthermore, a rigorous theoretical analysis of EigenVI’s convergence properties and error bounds would strengthen its foundation. Finally, investigating applications to diverse Bayesian models, including those with complex dependencies, and comparing EigenVI’s performance against a wider range of state-of-the-art BBVI methods in extensive benchmarks would solidify its position in the field.

More visual insights

#

More on figures

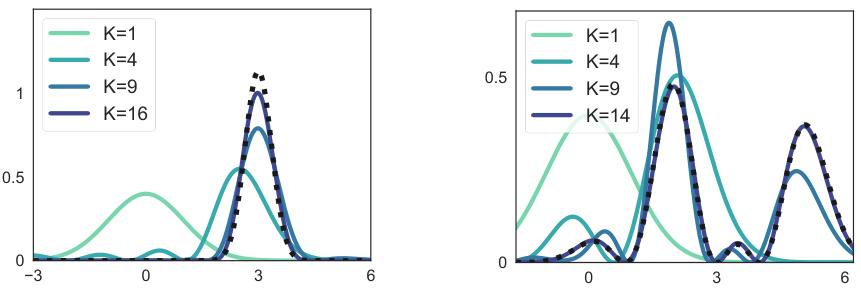
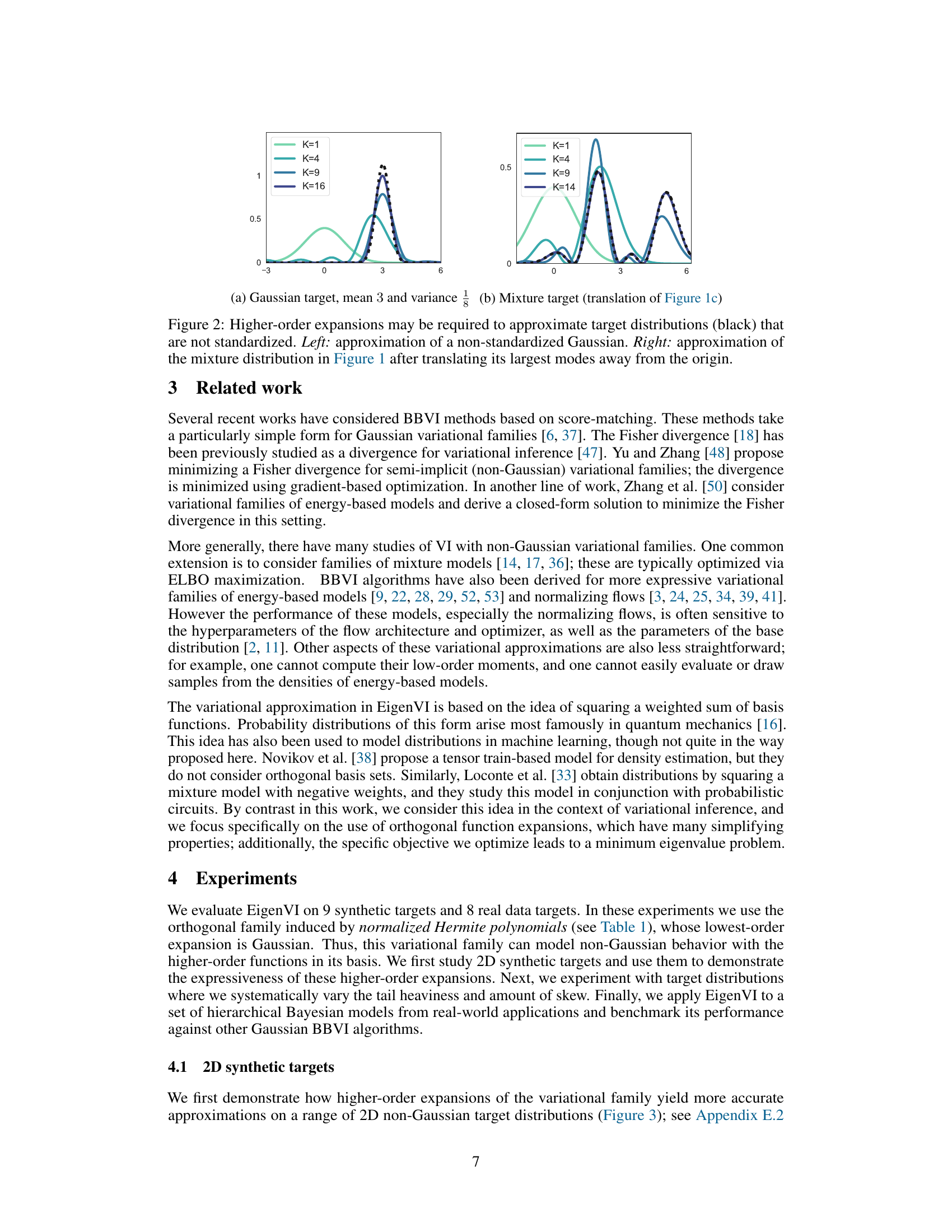
This figure demonstrates how orthogonal function expansions of various orders and from different families (Legendre polynomials, Fourier series, and Hermite polynomials) can approximate various target probability distributions. Each row presents a different target distribution and shows how the approximation improves as more terms are included in the expansion. The black dashed curves show the target distributions, while the colored curves illustrate approximations of increasing order (i.e., number of basis functions). This visualizes the expressiveness of the proposed method for approximating various types of distributions.

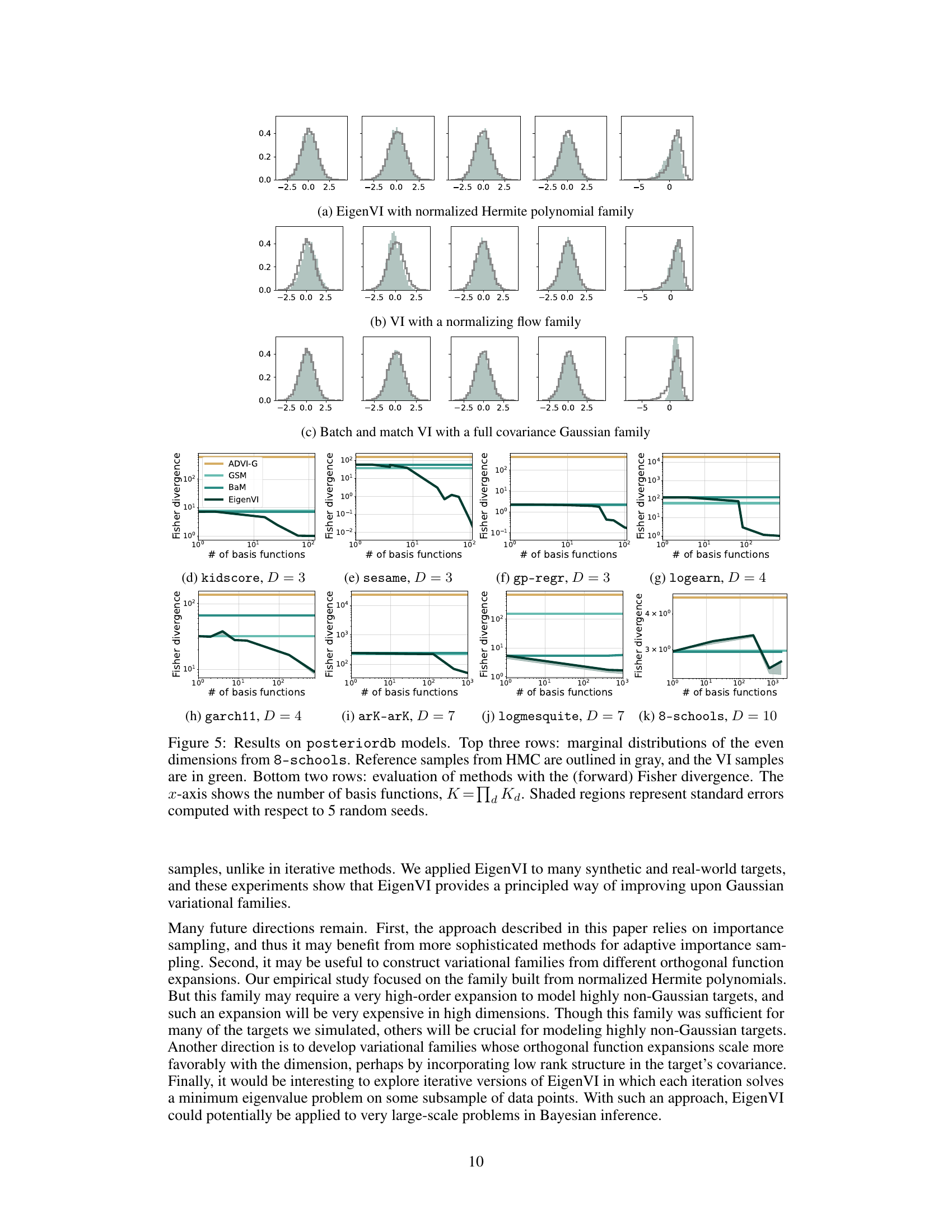
This figure compares the performance of EigenVI against a standard score-based VI method using Gaussian variational family for approximating three different 2D distributions: a 3-component Gaussian mixture, a funnel distribution, and a cross distribution. Each row represents a different target distribution. The first column shows the target distribution. The second column shows the approximation using score-based VI with a Gaussian variational family. The remaining columns (3-5) show the approximations obtained by EigenVI with increasing number of basis functions (K = K1K2). KL(p; q) values are provided for each approximation, quantifying the difference between the approximation and the target distribution. EigenVI demonstrates improved accuracy with a higher number of basis functions.

This figure presents a study on the performance of EigenVI on synthetic data generated using the sinh-arcsinh distribution, which allows for control over skewness and tail heaviness. Panel (a) visually displays three 2D target distributions and their corresponding EigenVI approximations. Panels (b) and (c) show the KL divergence (a measure of the difference between the true and approximated distributions) for different numbers of basis functions (K) used in EigenVI, comparing its performance to ADVI and BaM (both Gaussian-based methods), for dimensions 2 and 5 respectively. The results demonstrate EigenVI’s ability to accurately model distributions with varying degrees of non-Gaussianity.

This figure compares the performance of EigenVI and a Gaussian variational family for approximating various 2D probability distributions. The three rows show different target distributions: a three-component Gaussian mixture, a funnel shape, and a cross shape. The first column displays the target distributions, while the following columns present their approximations using a Gaussian variational family (score-based VI) and EigenVI with increasing numbers of basis functions (K = K1*K2). The KL divergence (KL(p;q)) is provided for each approximation to measure the closeness to the target distribution.

This figure compares the performance of EigenVI and a Gaussian variational family for approximating three different 2D target distributions: a 3-component Gaussian mixture, a funnel distribution, and a cross distribution. Each row represents one target distribution with its approximation by Gaussian score-based VI and EigenVI using increasing numbers of basis functions (K). KL divergence (KL(p; q)) is shown for each approximation, illustrating EigenVI’s ability to achieve lower KL values with more basis functions, indicating better approximation accuracy.

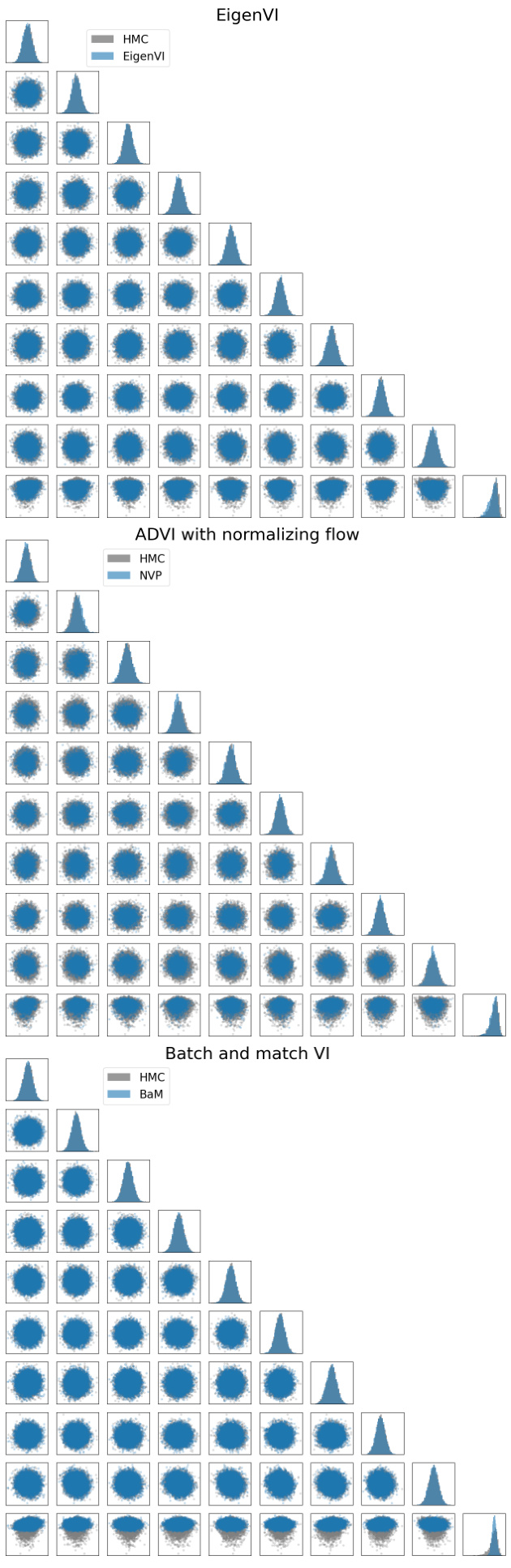
This figure demonstrates the performance of EigenVI on three 2D synthetic target distributions: a 3-component Gaussian mixture, a funnel distribution, and a cross distribution. Each row shows a different target distribution, with the first column displaying the true distribution. Subsequent columns illustrate the results of different variational inference methods, using both a Gaussian variational family and the EigenVI family with increasing numbers of basis functions (K). The KL divergence is reported for each approximation to quantify the closeness between the approximation and the true distribution. The results show that EigenVI, with sufficient basis functions, produces more accurate approximations compared to the Gaussian variational family.

This figure compares the performance of EigenVI and a Gaussian variational family on three different 2D target distributions: a Gaussian mixture, a funnel, and a cross. Each row shows the target distribution and then four different approximations: one from a Gaussian variational approximation using score-based VI and then three using EigenVI with an increasing number of basis functions (K). KL divergence is used to measure the closeness of approximation, with lower values indicating better performance. The results show that EigenVI yields better approximation compared to the Gaussian approach.

This figure visualizes the results of applying EigenVI to 5D sinh-arcsinh normal distributions with varying levels of skew and tail weight. The top row shows the true target distributions, demonstrating different degrees of non-Gaussianity. The bottom row displays the corresponding approximations generated by EigenVI, along with the Kullback-Leibler (KL) divergence values quantifying the difference between the true and approximated distributions. The figure illustrates EigenVI’s ability to model complex, non-Gaussian distributions in higher dimensions.

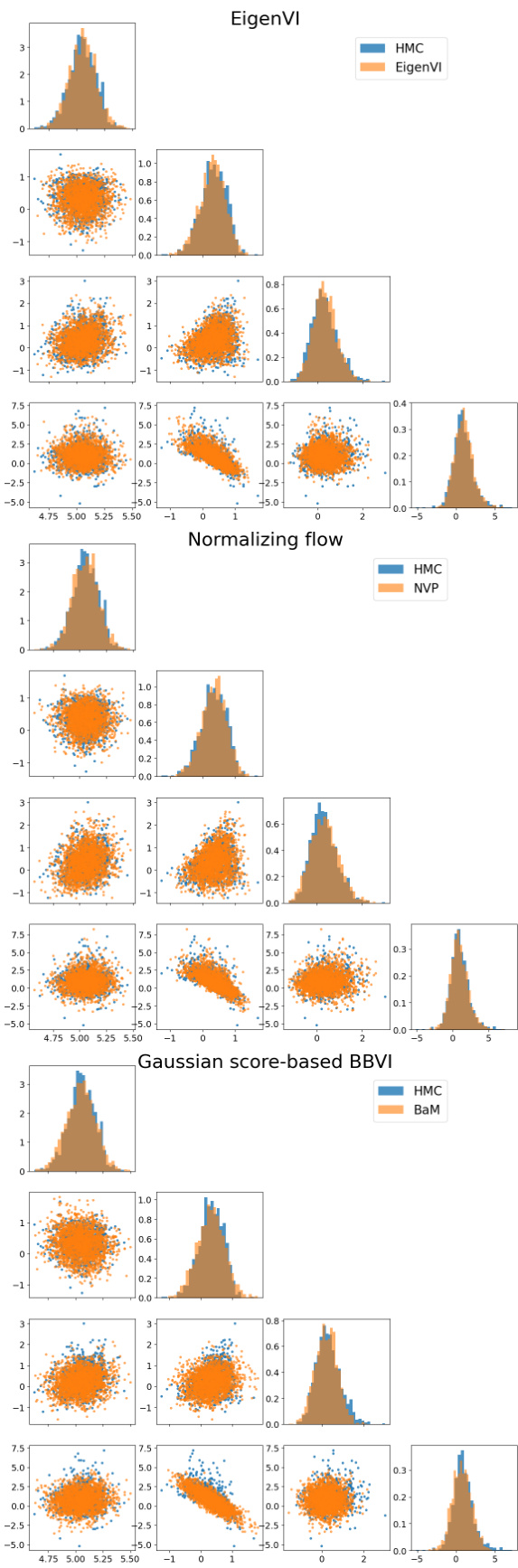
This figure compares the performance of EigenVI and score-based VI with a Gaussian variational family on three different 2D target distributions: a 3-component Gaussian mixture, a funnel distribution, and a cross distribution. For each target distribution and method, the figure shows the target distribution and several approximations from EigenVI at increasing values of K (K1 and K2 being the number of basis functions used in each dimension, such that K = K1K2). The Kullback-Leibler divergence (KL(p;q)) between the true distribution and the approximation is also given for each. The results show that EigenVI produces better approximations, particularly with increasing K.

This figure compares the performance of EigenVI and score-based VI with a Gaussian variational family on three different 2D target distributions: a 3-component Gaussian mixture, a funnel distribution, and a cross distribution. It demonstrates how increasing the number of basis functions (K) in EigenVI leads to progressively better approximations of the target distribution, as measured by the Kullback-Leibler (KL) divergence. The Gaussian variational family serves as a baseline, showing the advantage of EigenVI’s flexibility in handling complex, non-Gaussian distributions.

Full paper

#