Deep Submodular Peripteral Networks

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel and efficient method for learning submodular functions, a crucial problem in machine learning with many real-world applications. The proposed approach addresses the limitations of existing methods by leveraging graded pairwise comparisons and deep learning, opening new avenues for research in active learning, experimental design, and other areas that utilize submodular functions.

Visual Insights

#

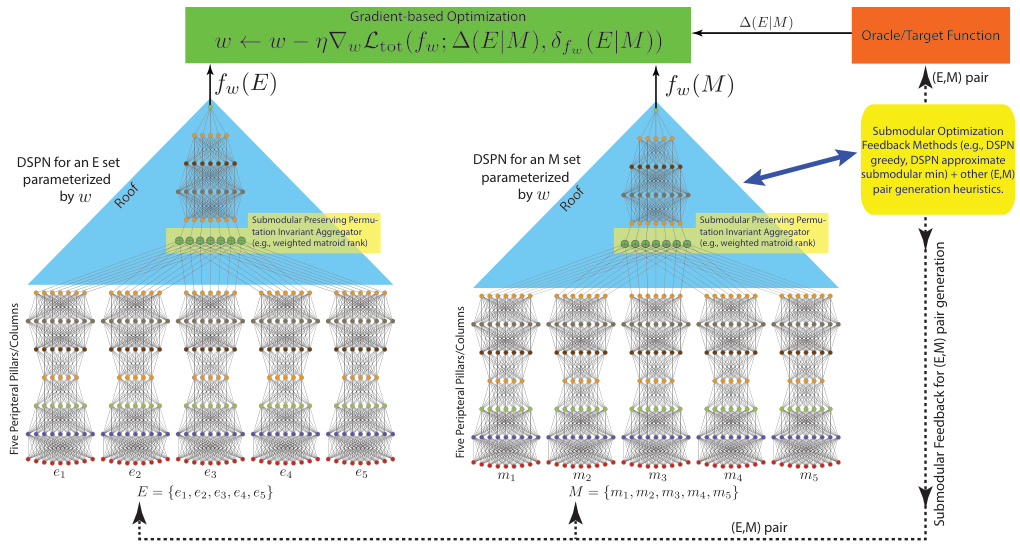
This figure illustrates the architecture of a Deep Submodular Peripteral Network (DSPN) and its training process. Two DSPNs, one for set E and one for set M, share the same parameters (w). Each DSPN consists of five peripteral pillars (input layer), a submodular-preserving permutation-invariant aggregator, and a roof (output layer). The E and M sets are input to their respective DSPNs. The output from each DSPN, fw(E) and fw(M), is used with the oracle/target function Δ(E|M) to calculate the peripteral loss. Gradient-based optimization adjusts the shared parameters (w) to minimize this loss. Submodular optimization feedback mechanisms are used for the sampling of E-M pairs, to guide the training process and ensure that information from the oracle/target is effectively transferred to the learner.

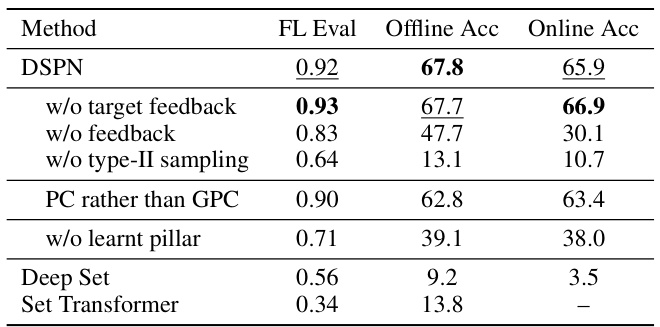
This table presents ablation studies on the Imagenet100 dataset to assess the impact of different components of the proposed DSPN framework. It compares the performance of the full DSPN model against variations that remove components such as feedback, type-II sampling, or the learnt pillar. It also contrasts using graded pairwise comparisons (GPC) against binary pairwise comparisons (PC) and compares the DSPN against other baseline models (Deep Sets and Set Transformers). The results highlight the importance of each component for optimal performance.

In-depth insights

#

Submodular Function Learning

#

Submodular function learning is a significant challenge in machine learning due to the complex nature of submodular functions and the computational difficulty in optimizing them. Many real-world applications benefit from submodularity, but acquiring a suitable submodular function for a given task remains a hurdle. This area is crucial because directly optimizing submodular functions is often computationally expensive, especially for large datasets. Existing methods often rely on assumptions about the function’s structure, limiting their applicability and scalability. Consequently, research focuses on efficient learning strategies that leverage data to directly estimate or approximate a submodular function or indirectly learn a function that satisfies submodularity properties. Recent advancements include using deep learning architectures combined with loss functions tailored to submodular properties, exploring graded pairwise comparisons and learning scalings from oracles, and investigating the use of active learning to reduce the cost of obtaining data. Developing scalable and generalizable learning methods for submodular functions is an active area of research as it has the potential to unlock new possibilities across various domains, including machine learning, computer vision, and natural language processing.

Deep Submodular Nets

#

Deep Submodular Nets represent a significant advancement in the field of machine learning, addressing the challenge of learning submodular functions efficiently and effectively. The core innovation lies in combining deep learning architectures with the properties of submodularity. This approach offers several key advantages. First, it leverages the power of deep learning to learn complex representations from data, effectively capturing intricate relationships between elements. Second, the submodularity constraint ensures that the learned function exhibits the desirable property of diminishing returns, leading to theoretically sound and practically efficient optimization algorithms. Third, the combination of deep learning and submodularity allows for the creation of highly scalable and expressive submodular functions applicable to large-scale real-world problems. Deep Submodular Nets show promise across various machine learning tasks where submodularity is beneficial, including summarization, active learning, and experimental design. The ability to learn such functions from data, rather than relying on handcrafted ones, is a major step forward. However, further research is needed to fully explore the capabilities of Deep Submodular Nets and their limitations. Areas for future investigation include improving the efficiency of training, exploring different architectural designs, and addressing the potential computational cost for very large datasets.

GPC-Style Loss

#

The proposed GPC-style loss function is a novel approach to training deep submodular peripteral networks (DSPNs). It leverages numerically graded pairwise comparisons, moving beyond binary preferences to incorporate the degree of preference between sets. This offers a significant advantage over traditional contrastive learning methods, as it captures more nuanced information. The key innovation lies in using a ratio of the learner’s score to the oracle’s score, resulting in a positive quantity for aligned preferences and a negative value otherwise. This ratio is then incorporated into a loss function that emphasizes large differences between learner and oracle preferences. This loss function is carefully designed to be numerically stable and handles cases of indifference efficiently, which is a notable improvement over methods solely relying on binary comparisons. The use of GPC-style feedback is crucial for efficient knowledge transfer from expensive oracles to the parametric learner, enabling the training of a powerful and scalable submodular function model. Finally, the methodology has broader applications beyond submodular function learning, such as in preference learning and RLHF.

Active Set Sampling

#

Active Set Sampling strategies in machine learning aim to intelligently select subsets of data for model training or other tasks, unlike passive methods that sample randomly or systematically. The core idea is to leverage feedback from the model or a target function to guide the selection process, focusing on subsets deemed most informative or beneficial. This often involves an iterative procedure where sets are evaluated, feedback is obtained (e.g., model performance, function value, human preferences), and then subsequent sets are chosen to maximize information gain or reduce uncertainty. Submodularity is often used to guide the selection process, thanks to its diminishing returns property, which makes it well-suited for efficiently optimizing subset selection. Different feedback mechanisms can be employed, including model predictions, function evaluations, or human annotations, depending on the problem and available resources. Active Set Sampling can be particularly useful in situations with high data costs or limitations, enabling efficient utilization of limited resources. The strategies must consider the balance between exploration (exploring diverse regions of the data space) and exploitation (focusing on promising areas identified via previous evaluations). Active sampling strategies enhance the efficiency and effectiveness of machine learning workflows in various applications.

Future Work

#

The paper’s ‘Future Work’ section presents exciting avenues for extending deep submodular peripteral networks (DSPNs). Scaling DSPNs to massive datasets is crucial, potentially leveraging techniques like coresets to manage computational cost and improve efficiency. Exploring the use of more sophisticated sampling strategies, beyond the heuristics and active learning techniques presented, could enhance performance and model generalization. A significant opportunity lies in applying DSPNs to diverse domains, such as online streaming applications, where real-time summarization or active learning is critical. Investigating alternative oracle queries and loss functions would broaden the applicability of the DSPNs framework, going beyond the graded pairwise comparisons to potentially more efficient or more informative alternatives. Further theoretical research, addressing the representational capacity of DSPNs, and investigating the conditions under which DSPNs can express all monotone non-decreasing submodular functions, is crucial to establish the fundamental limits and capabilities of this novel architecture. Finally, integrating DSPNs with other machine learning techniques for tasks like multi-modal learning or reinforcement learning could reveal new synergies and open up new avenues of research.

More visual insights

#

More on figures

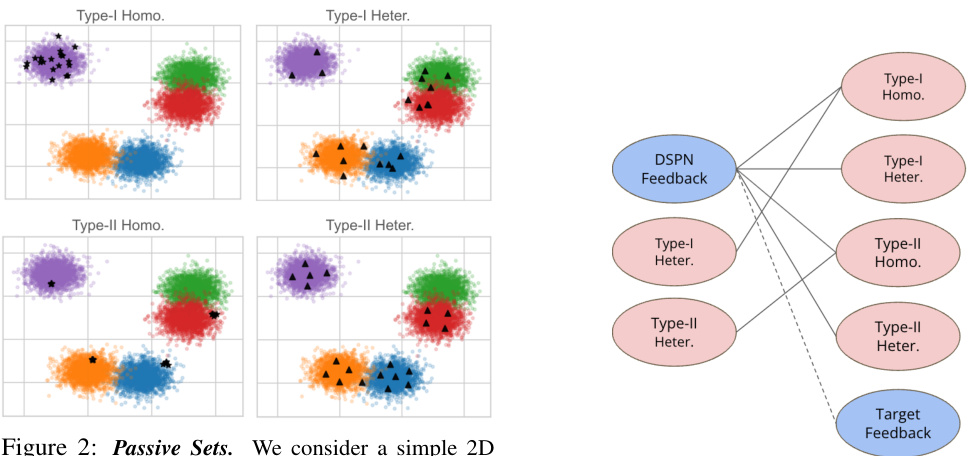
This figure illustrates different strategies for passively sampling sets from a 2D dataset with 5 clusters. Type-I sampling shows homogeneous sets (all points from one cluster) and heterogeneous sets (points from all clusters). Type-II sampling demonstrates the same, but with the ground set restricted to a subset of the clusters. This distinction helps the DSPN learn intra-class and inter-class relationships, respectively.

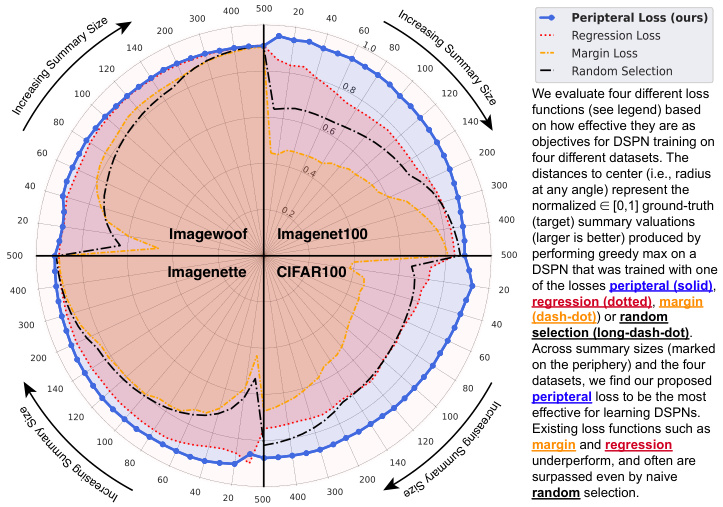
This figure shows a comparison of four different loss functions used for training Deep Submodular Peripteral Networks (DSPNs). The radial distance from the center represents the normalized ground-truth (target) summary valuation achieved by performing greedy maximization on the target function. The angle represents different summary sizes (budgets). The results indicate that the proposed peripteral loss outperforms other methods (regression, margin, random selection) across various summary sizes and datasets.

This figure compares the performance of different summarization techniques in an offline experimental design setting. The goal is to select a subset of unlabeled data for labeling to train a linear model. The x-axis represents the size of the training dataset (the summary), and the y-axis represents the accuracy of the trained linear model. The figure shows that the proposed Deep Submodular Peripteral Network (DSPN) method outperforms existing techniques (k-center, CRAIG, random) in achieving high accuracy, even approaching the performance of the optimal ‘Target FL’ method which has access to information not available to the other methods. This demonstrates DSPN’s effectiveness in selecting informative training samples.

This figure compares the performance of different summarization methods in an online setting, where data arrives sequentially. The y-axis shows the accuracy of a linear model trained on the selected subset, and the x-axis shows the size of the training dataset (budget). The DSPN-online method significantly outperforms baseline methods (Reservoir and VeSSAL) and achieves performance comparable to the offline DSPN approach. This demonstrates that the DSPN is effective at selecting informative samples from a data stream for training.

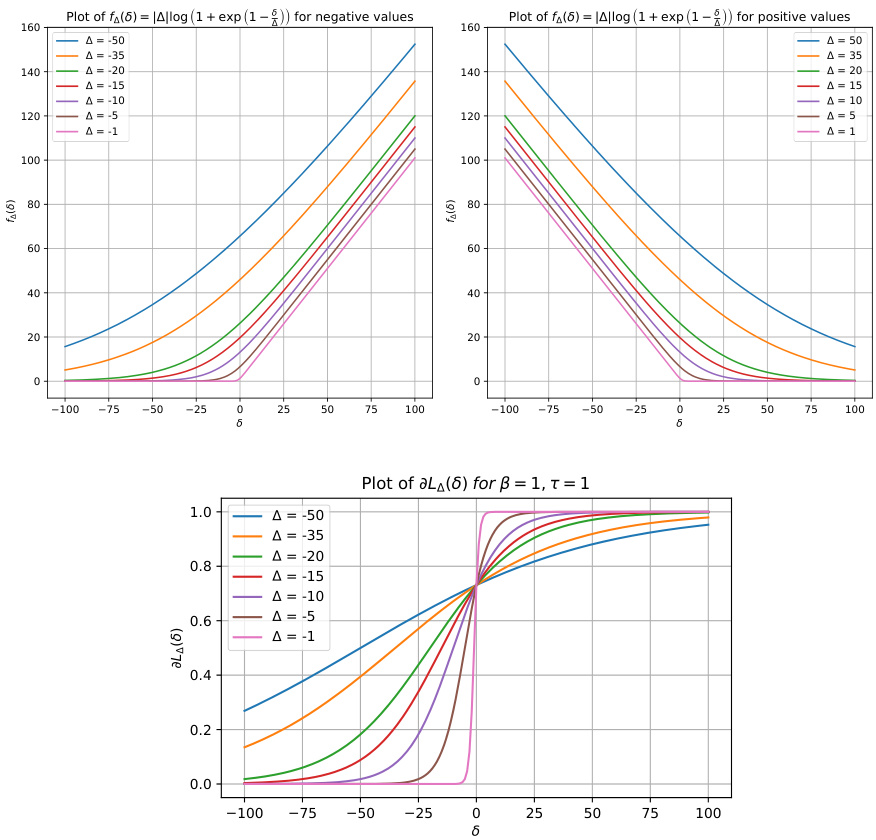
This figure shows plots of the peripteral loss function and its gradient with respect to δ for various values of the margin Δ and different values of the hyperparameters β and τ. The plots illustrate how the loss changes as a function of δ, demonstrating the impact of the margin and hyperparameters on the loss function’s curvature and smoothness. The gradients are also shown, giving insights into the behavior of the loss function’s optimization.

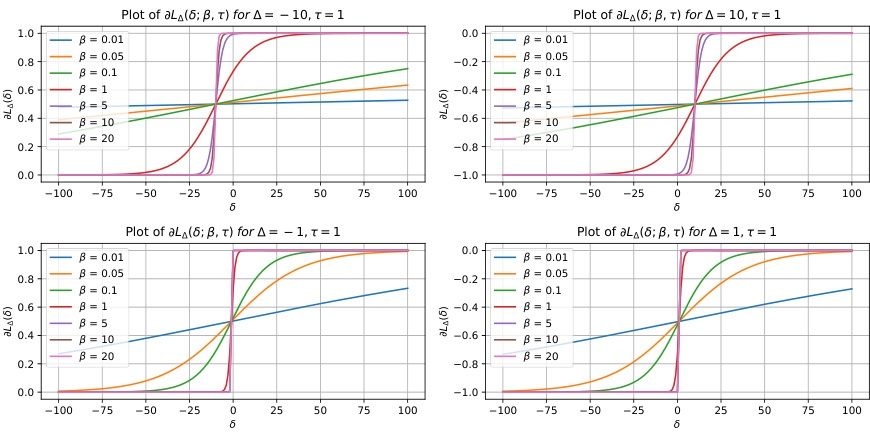
This figure shows two plots. The left plot shows the peripteral loss for different values of β (the smoothing parameter) and for positive and negative margins. The right plot shows the gradient of the peripteral loss with respect to δ (the difference between the learner and oracle predictions) for the same set of β values and margins. The plots illustrate how the hyperparameter β influences the smoothness of the loss function and its gradient, affecting the stability and convergence of the optimization process.

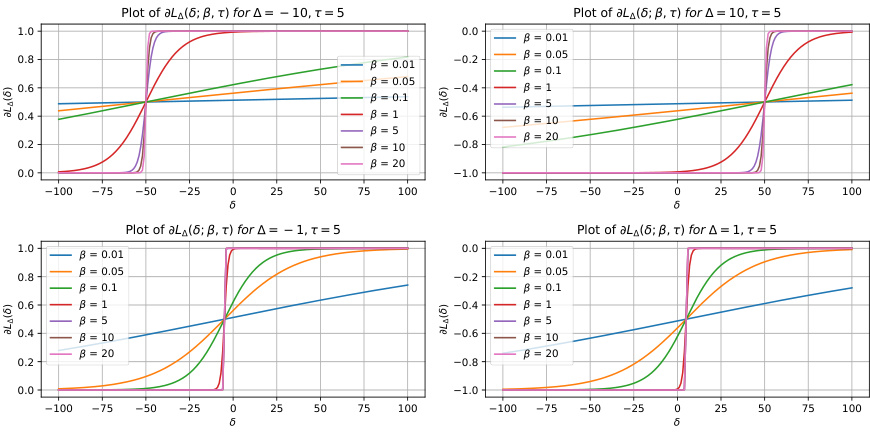
This figure shows plots of the peripteral loss function (LΔ;β,τ,κ,ε(δ)) and its gradient for various values of the margin (Δ) and different hyperparameter settings (β). The plots illustrate how the loss and gradient behave for both positive and negative margins, and how the hyperparameters control the curvature and smoothness of the loss function. It helps to visualize the behavior of the loss function for different inputs and how the hyperparameters affect the loss landscape during the training process.

This figure illustrates the architecture of a Deep Submodular Peripteral Network (DSPN) and its training process. Two copies of the DSPN are shown, one for set E and another for set M. Each DSPN consists of pillars (feature extractors), an aggregation stage (weighted matroid rank function), and a deep submodular function (DSF) roof. The training involves iterative optimization using a novel peripteral loss, leveraging graded pairwise comparisons from an oracle. The figure visually depicts the flow of information from input data through the DSPN to the final output, emphasizing the interaction between the two DSPN instances and the oracle feedback during training. Appendix G provides additional details.

This figure shows the class distributions of four image datasets (Imagenette, Imagewoof, CIFAR-100, and Imagenet100) after adding duplicates to make them heavily class-imbalanced. The x-axis represents the classes, and the y-axis represents the number of samples per class. The distributions are shown to illustrate the uneven representation of classes in these datasets, which serves as a more challenging and realistic test for the proposed DSPN model.

This figure qualitatively analyzes the learned features of the DSPN model and compares them to CLIP features. It shows the top and bottom 10 images ranked by randomly selected features from both DSPN and CLIP. The DSPN features show a strong correlation to class, indicating that they capture count-like attributes, while CLIP features show weaker correlations.

More on tables

This table lists the values of the hyperparameters λ₁, λ₂, λ₃, and λ₄ used in the augmentation regularizer (Equation 2) and redundancy regularizer (Equation 3) for each of the four datasets (Imagenette, Imagewoof, CIFAR100, and Imagenet100). These hyperparameters control the strength of the regularization terms in the overall loss function used to train the Deep Submodular Peripteral Networks (DSPNs).

This table shows the normalized facility location (FL) evaluation results for different values of the hyperparameter β and various summary sizes (k). The normalized FL evaluation measures how well the learned DSPN model approximates the target FL function. Higher values indicate better approximation.

This table presents the normalized Facility Location (FL) evaluation results for different summary sizes (k) and values of the hyperparameter τ. The results show how the performance of the model varies with different values of τ for different summary sizes. It demonstrates the sensitivity of the model’s performance to changes in the hyperparameter τ.

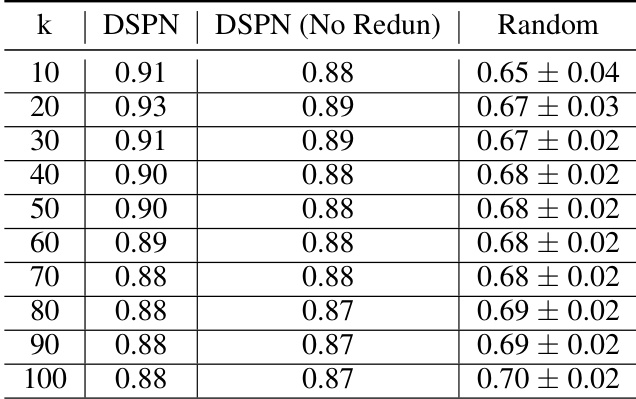
This table shows the normalized facility location (FL) evaluation results on the CIFAR100 dataset for different summary sizes (k). It compares the performance of the DSPN model with and without redundancy regularizers (λ3 and λ4) against a random baseline. The results demonstrate that the redundancy regularizers improve performance but are not essential, indicating robustness of the DSPN approach.

Full paper

#