↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Current neural rendering techniques like 3D Gaussian Splatting rely on heuristics for Gaussian placement, leading to suboptimal results and heavy reliance on good initialization. These heuristics involve cloning, splitting, and pruning strategies that lack theoretical grounding and can be difficult to tune. This results in inefficient use of Gaussians, poor rendering quality, and a high dependence on initial conditions.
This paper addresses these issues by rethinking 3D Gaussian Splatting as Markov Chain Monte Carlo (MCMC) sampling. By introducing noise and reformulating the update rules as Stochastic Gradient Langevin Dynamics (SGLD), the authors achieve a more principled and robust method. This involves a new relocation scheme that replaces heuristics, encouraging efficient use of Gaussians with L1 regularization. Experiments show that the proposed method improves rendering quality, provides easier control over the number of Gaussians, and is more robust to initialization, outperforming existing techniques on various datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in neural rendering and MCMC because it bridges the gap between heuristic-based Gaussian Splatting methods and principled MCMC sampling, leading to improved rendering quality, easier Gaussian control, and robustness to initialization. It opens avenues for applying MCMC techniques in other neural rendering problems.
Visual Insights#
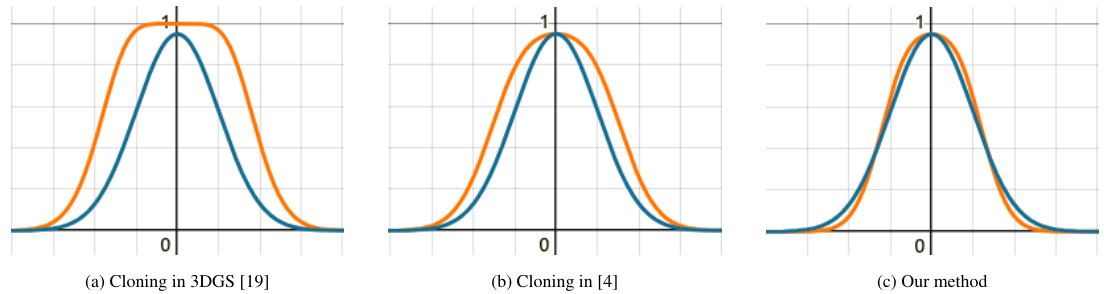
This figure compares three different strategies for cloning or respawning Gaussians in the context of Markov Chain Monte Carlo (MCMC) sampling. The original 3D Gaussian Splatting method (a) and a recent variant (b) both significantly alter the shape of the Gaussian after cloning, making them unsuitable for MCMC. In contrast, the proposed method (c) maintains a similar Gaussian shape, preserving the sample probability and ensuring a valid MCMC update.
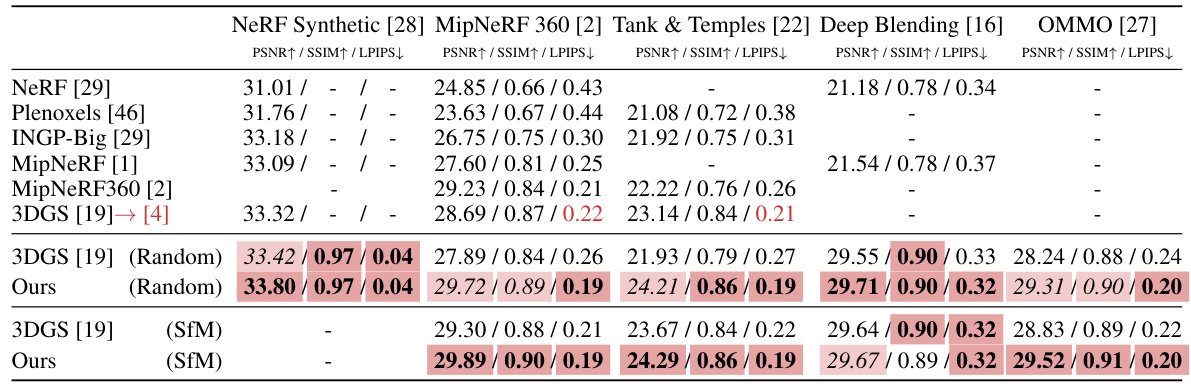
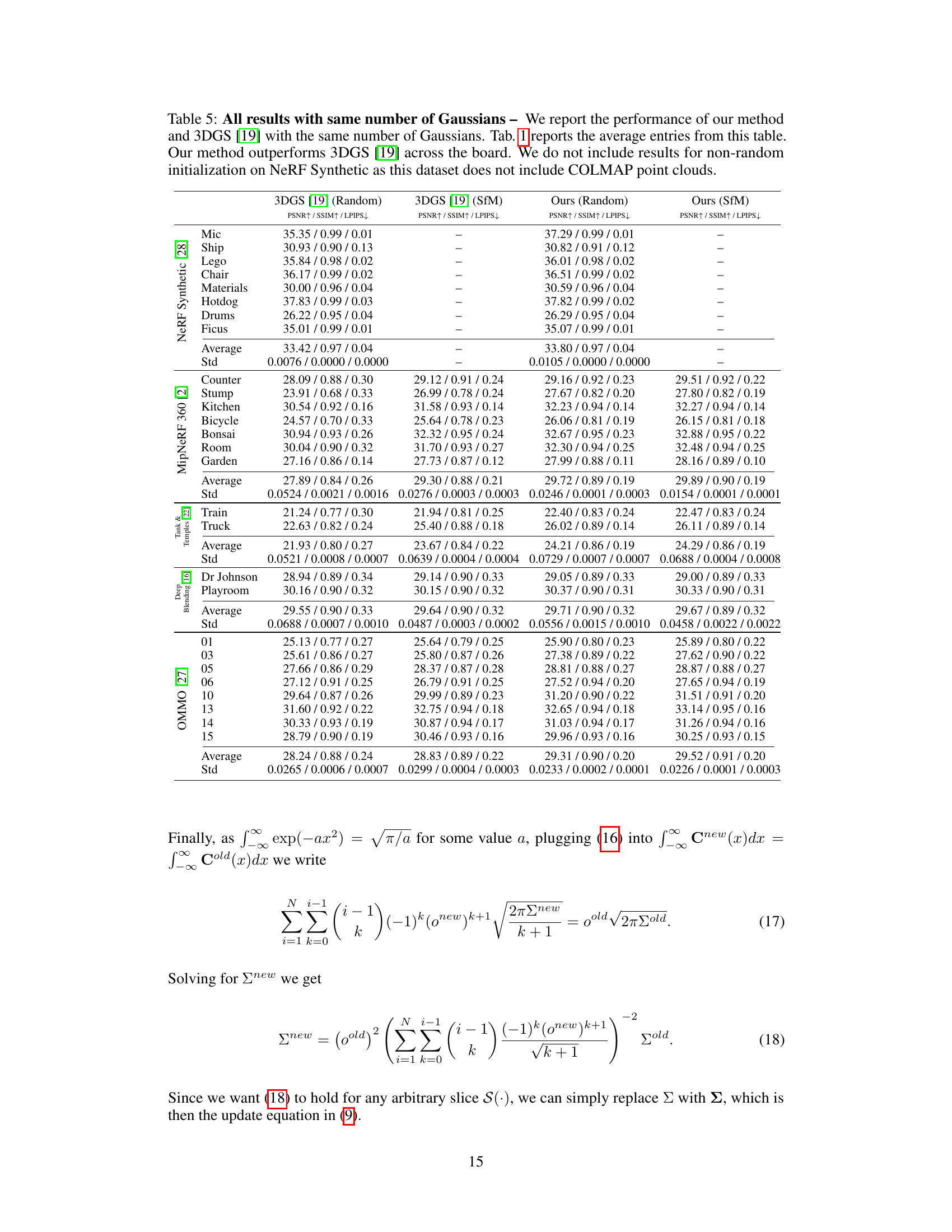
This table presents a quantitative comparison of the proposed method against several baselines on various standard datasets for neural rendering. The key metric used is PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index Metric), and LPIPS (Learned Perceptual Image Patch Similarity). The comparison is made while ensuring the number of Gaussians used is consistent across all methods. The results highlight that the proposed method significantly outperforms existing techniques, especially when initialized randomly.
In-depth insights#
MCMC in 3DGS#
The integration of Markov Chain Monte Carlo (MCMC) methods into 3D Gaussian Splatting (3DGS) offers a novel perspective on neural rendering. Instead of relying on heuristic-based cloning and splitting strategies for Gaussian placement, MCMC frames the Gaussian updates as stochastic sampling from an underlying probability distribution representing the scene. This probabilistic approach elegantly addresses the limitations of previous methods, which often suffered from poor-quality renderings due to reliance on initialization and manually-tuned parameters. By viewing densification and pruning as deterministic state transitions within the MCMC framework, the need for these heuristic-driven strategies is eliminated. The introduction of noise into the Gaussian updates, transforming them into Stochastic Gradient Langevin Dynamics (SGLD) updates, facilitates efficient exploration of the probability space and robust sampling. This results in improved rendering quality, better control over the number of Gaussians, and robustness to initialization, offering a more principled and theoretically sound approach to neural scene representation than traditional heuristic-based 3DGS.
SGLD for Rendering#
Employing Stochastic Gradient Langevin Dynamics (SGLD) for neural rendering offers a compelling alternative to traditional optimization methods. SGLD introduces stochasticity, effectively transforming the parameter search into a Markov Chain Monte Carlo (MCMC) process. This approach fosters exploration of the probability distribution underlying the scene representation, mitigating reliance on carefully engineered heuristics for Gaussian placement. By incorporating noise, SGLD naturally handles densification and pruning of Gaussians, simplifying the training process and enhancing robustness to initialization. The inherent exploration of SGLD allows for more effective sampling of high-probability regions, leading to superior rendering quality. This probabilistic approach also presents advantages in terms of convergence speed and memory efficiency, especially when dealing with complex scenes and high-dimensional parameter spaces. However, challenges remain in appropriately tuning the noise parameter to maintain balance between exploration and exploitation, and further investigation is warranted to fully leverage SGLD’s potential within the context of high-quality, real-time rendering.
Heuristic-Free 3DGS#
The concept of “Heuristic-Free 3DGS” presents a significant advancement in 3D Gaussian Splatting. Traditional 3DGS methods rely heavily on heuristics for tasks like Gaussian placement, cloning, and pruning. This heuristic reliance leads to suboptimal results, sensitivity to initialization, and difficulty in controlling the number of Gaussians. By framing 3D Gaussian Splatting as a Markov Chain Monte Carlo (MCMC) process, this heuristic-free approach introduces a principled probabilistic framework. This allows for more robust and efficient Gaussian manipulation, replacing ad-hoc rules with mathematically sound updates that promote better exploration of the scene’s representation. The introduction of a regularizer further encourages efficient use of Gaussians, preventing unnecessary computation by promoting the removal of redundant ones. The approach demonstrates improvements in rendering quality, robustness to initialization, and better control over model complexity, signifying a substantial shift towards more principled and less heuristic-driven neural rendering techniques.
Gaussian Relocation#
Gaussian relocation, within the context of 3D Gaussian splatting for neural rendering, presents a crucial strategy for efficient and high-quality scene representation. It directly addresses the limitations of heuristic-based cloning and splitting methods by offering a principled approach. Instead of relying on arbitrary rules for creating or removing Gaussians, relocation intelligently moves underutilized or ‘dead’ Gaussians to regions of higher importance, thereby dynamically adjusting the representation’s density and improving rendering quality. This approach is particularly valuable because it maintains the overall probability distribution of the Gaussian sample set, ensuring that the training process remains stable and effective. By carefully relocating Gaussians, the method avoids the instability and suboptimal rendering results that can arise from the heuristic-based approaches in standard 3D Gaussian splatting, leading to both improved quality and control over the model’s complexity.
Regularization Effects#
Regularization techniques are crucial for preventing overfitting in machine learning models. In the context of 3D Gaussian splatting, regularization helps to control the complexity of the representation by limiting the number of Gaussians used. Applying L1 regularization on the opacity and covariance of the Gaussians encourages sparsity, effectively removing unnecessary Gaussians and reducing computational cost. This is particularly beneficial when dealing with scenes containing many small or insignificant details that might otherwise overwhelm the model with an excessive number of Gaussians. The regularization strength is a hyperparameter that can be tuned to find the optimal balance between model accuracy and complexity. Careful selection of the regularization hyperparameters is key to achieving a robust and efficient model. It is a delicate balance: insufficient regularization might lead to overfitting and poor generalization, while excessive regularization could hinder the model’s ability to capture important features of the scene, resulting in decreased rendering quality.
More visual insights#
More on figures
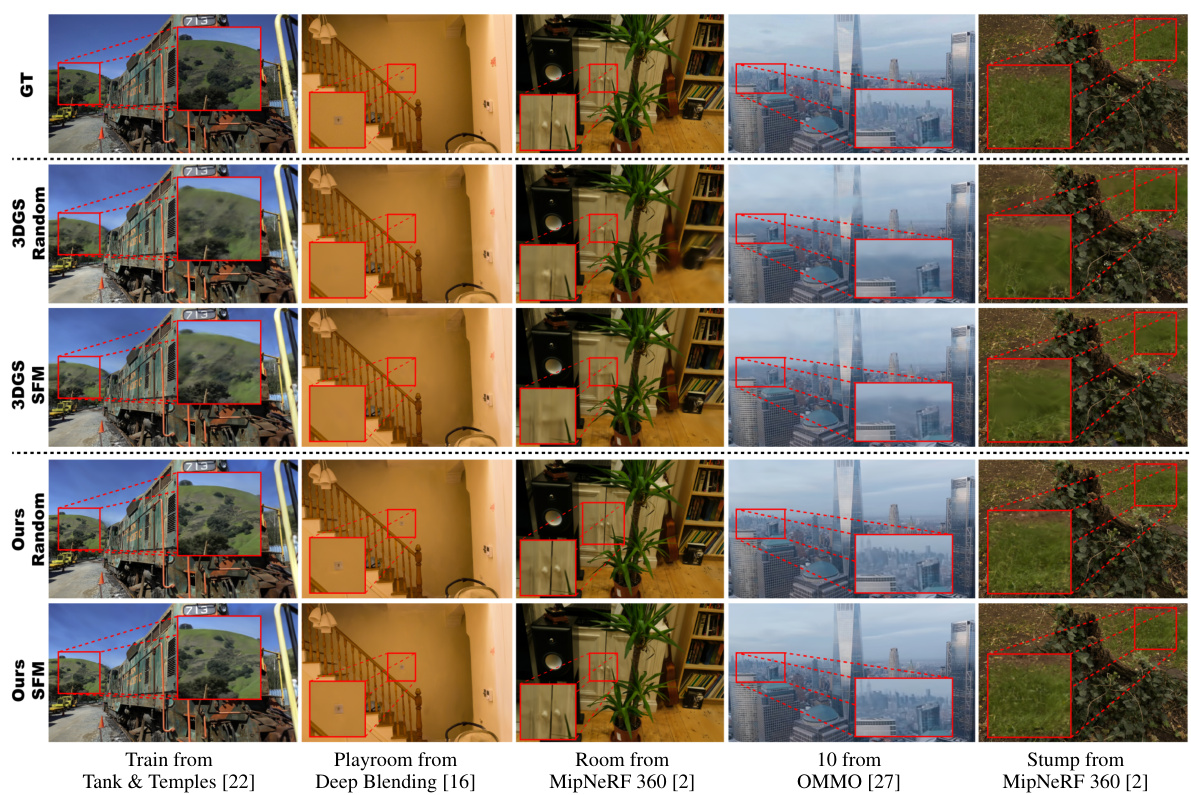
This figure shows a qualitative comparison of novel view rendering results between the original 3D Gaussian Splatting method and the proposed method. The comparison is done using the same number of Gaussians for both methods and using two different initialization strategies (random and Structure from Motion (SfM)). The figure highlights the superior detail and overall quality achieved by the proposed MCMC approach, particularly noticeable in close-ups of specific regions within the rendered images.
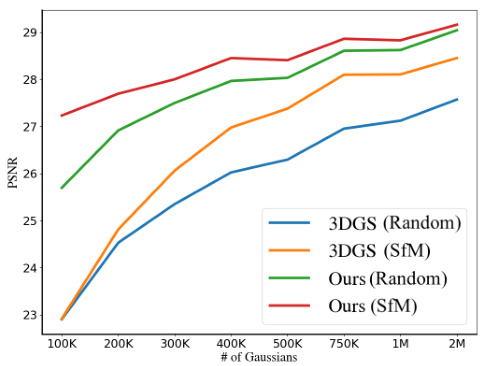
This figure shows the PSNR (Peak Signal-to-Noise Ratio) performance of 3D Gaussian Splatting (3DGS) and the proposed method with varying numbers of Gaussians. The results are averaged across multiple datasets (excluding NeRF Synthetic). It demonstrates the impact of the number of Gaussians on the rendering quality, comparing the performance of the baseline 3DGS method with random and SfM (Structure-from-Motion) initialization against the proposed MCMC approach using the same initializations. The graph visually represents the improvement in PSNR achieved by the proposed method, especially with a limited budget of Gaussians.

This figure shows qualitative comparison of novel view rendering results between the proposed method and the baseline method (3DGS [19]) on various scenes with the same number of Gaussians. The proposed method demonstrates superior detail and reconstruction quality, highlighting the benefits of the MCMC framework and the removal of heuristic-based strategies.
More on tables

This table presents an ablation study, analyzing the impact of different components of the proposed method on the rendering quality using the MipNeRF 360 dataset. The experiment uses random initialization. The columns show the results for the baseline 3DGS method, the 3DGS method with the total loss function, the proposed method with the original loss function, the proposed method without noise, the proposed method with noise added to all parameters, and finally the full proposed method.

This table presents an ablation study on the initialization strategies for 3D Gaussian Splatting. It compares the performance (PSNR, SSIM, LPIPS) of the proposed method and the original 3DGS method when initialized with random point clouds versus point clouds from Structure-from-Motion (SfM). The key finding is that the proposed method’s performance is consistent regardless of the initialization type, while the original 3DGS method shows a significant performance difference between random and SfM initializations.

This table compares the training time and PSNR (Peak Signal-to-Noise Ratio) of the proposed method with 3DGS [19] for different settings of the opacity regularizer (λo) and maximum number of Gaussians. The results show that the proposed method achieves comparable or better PSNR with significantly reduced training time.
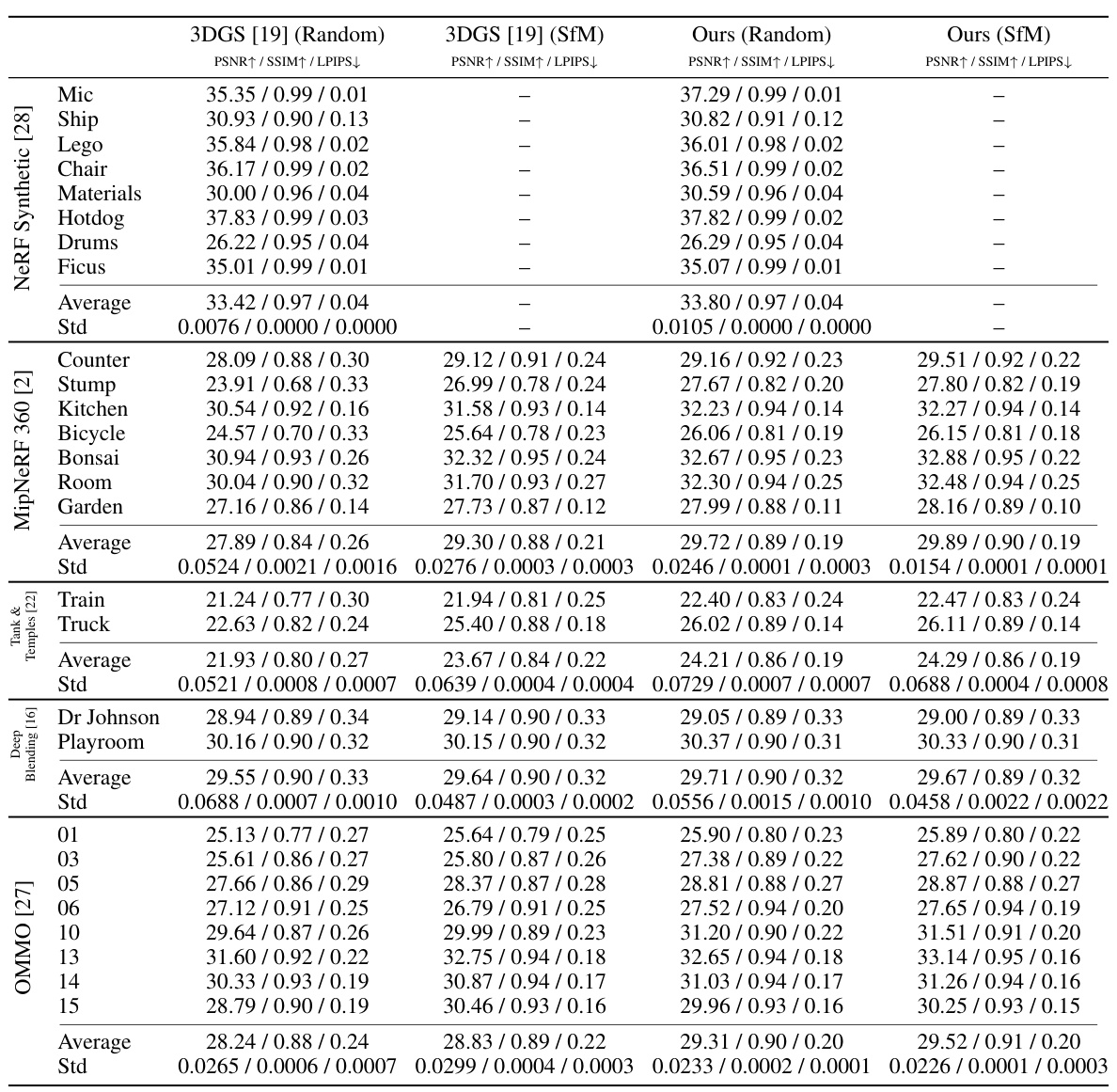
This table presents a quantitative comparison of the proposed method against various baselines on multiple datasets using the same number of Gaussians. It shows PSNR, SSIM, and LPIPS scores for each method and dataset, highlighting the best and second-best results. The results demonstrate the superior performance of the proposed method, especially when compared to the random initialization of 3DGS [19].
Full paper#