↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many AI fields utilize attention-based neural architectures, but their application to complex physical systems remains underexplored. These systems often involve discovering operators mapping between function spaces, posing a challenge as these inverse problems are frequently ill-posed. Existing methods often require problem-specific prior information, limiting their applicability.
The paper introduces a novel neural operator architecture called Nonlocal Attention Operator (NAO). NAO leverages the attention mechanism to extract global prior information from multiple systems, effectively addressing ill-posedness and rank deficiency. Empirically, NAO shows advantages over existing neural operators in terms of generalizability to unseen data and system states, offering a new perspective on understanding the attention mechanism itself and paving the way for learning more interpretable models of physical systems.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel neural operator architecture, NAO, that enhances the interpretability and generalizability of physics models. By addressing the ill-posed nature of inverse problems, NAO opens new avenues for discovering hidden physical laws from data, impacting various scientific and engineering domains. Its data-driven regularization and ability to handle unseen data resolutions are particularly significant for complex systems.
Visual Insights#
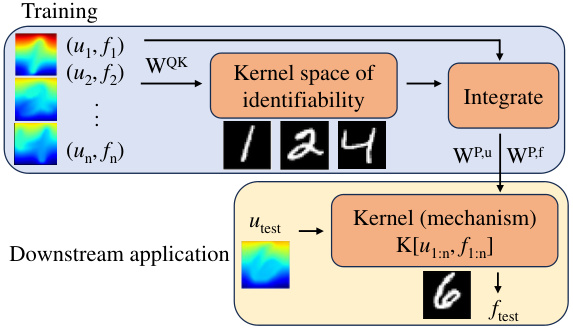
The figure illustrates the architecture of the Nonlocal Attention Operator (NAO). The training phase involves multiple input-output function pairs ((uᵢ, fᵢ)). These pairs are processed through a kernel map (the attention mechanism) to extract a global understanding of the underlying physical laws, creating a ‘kernel space of identifiability’. This knowledge is then used to construct a kernel (mechanism) K which acts as a nonlocal interaction operator that maps input function ‘utest’ to output function ‘ftest’. The downstream application utilizes this learned kernel for prediction on new, unseen data.
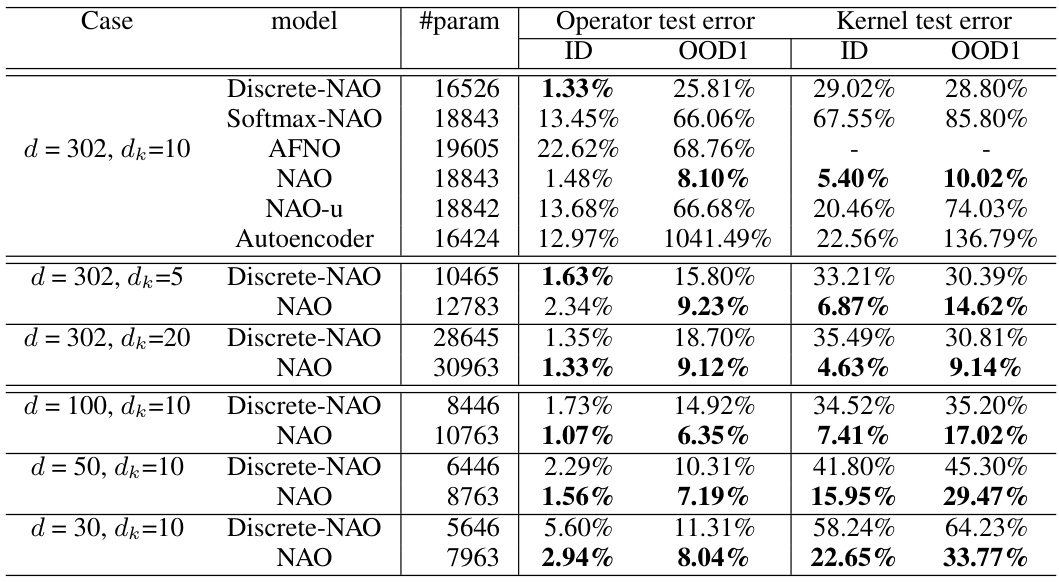
The table presents the results of experiments on radial kernel learning. It compares the performance of the proposed Nonlocal Attention Operator (NAO) against several baseline methods (Discrete-NAO, Softmax-NAO, AFNO, NAO-u, Autoencoder) in terms of operator and kernel test errors. The results are shown for different configurations, varying the token size (dk) and data resolution. The bold numbers indicate the best performance for each configuration. The table highlights that NAO is superior in handling the ill-posed nature of the inverse problem and provides resolution-invariant estimators, unlike the baseline methods.
In-depth insights#
NAO Architecture#
The Nonlocal Attention Operator (NAO) architecture cleverly integrates attention mechanisms within a neural operator framework. The core innovation lies in the data-dependent kernel map, learned via an attention mechanism, that simultaneously addresses both forward and inverse problem solving. This is achieved by using the attention mechanism to extract global prior information from training data generated across multiple physical systems. The kernel then acts as a regularizer, automatically suggesting an exploratory space for the solution to the inverse problem and enhancing generalizability. Instead of a fixed kernel, NAO learns a flexible kernel map parameterized by the attention mechanism, enabling the extraction of system-specific knowledge that enhances interpretability. This attention-based kernel map, therefore, provides the foundation for a powerful neural operator that moves beyond simple forward problem approximation and delves into the challenging realm of simultaneous forward and inverse problem solving, leading to a more robust and interpretable physical model.
Kernel Map’s Role#
The kernel map is a crucial component of the Nonlocal Attention Operator (NAO), acting as an inverse PDE solver. It learns a mapping from input-output function pairs to a kernel that characterizes the underlying physical system. This is achieved using an attention mechanism, enabling the NAO to extract global information from multiple systems. The learned kernel map is data-driven and doesn’t rely on prior knowledge of the specific physical laws. It suggests the exploratory space of the inverse problem, addressing ill-posedness and rank deficiency by implicitly encoding regularization and promoting generalizability to unseen data resolutions and system states. Essentially, it enables the NAO to learn both the forward (predictive) and inverse (discovery) aspects of the physical system simultaneously, improving the model’s interpretability and allowing for the discovery of hidden physical mechanisms.
Inverse PDE Solving#
Inverse PDE solving is a challenging ill-posed problem, often characterized by severe instability and non-uniqueness. Traditional methods struggle with high dimensionality and limited data, making accurate solutions difficult. Deep learning offers promising alternatives, but naive approaches often lack generalizability and interpretability. The paper’s proposed Nonlocal Attention Operator (NAO) seeks to address these issues. By leveraging the power of attention mechanisms and incorporating a data-dependent kernel, NAO aims to extract global information from training data, which improves regularization and generalizability. The approach focuses on simultaneously solving both forward and inverse problems, offering a pathway to discovering hidden physical laws directly from data. A key advantage is the ability to handle unseen system states and resolutions, overcoming limitations of conventional methods which require starting from scratch for each new problem. Ultimately, this approach aims to enhance the interpretability of data-driven physical models.
Generalizability Test#
A robust generalizability test for a machine learning model, especially one designed for physics modeling, should rigorously assess performance on unseen data and systems. This goes beyond simple accuracy metrics; it should probe the model’s ability to extrapolate to different resolutions, system configurations (e.g., varying material properties), and even entirely new physical phenomena not encountered during training. Zero-shot learning scenarios are crucial for evaluating true generalizability. The tests must also consider the ill-posed nature of inverse problems, which can be particularly challenging for physical systems; robustness to noise and data scarcity needs to be examined. Ideally, the test would analyze not only prediction accuracy but also the interpretability of the learned models. Does the discovered mechanism make sense physically? Can the model’s internal representations provide insights into the underlying physical processes? Addressing these aspects comprehensively provides a far more meaningful and useful evaluation than simply reporting high accuracy on seen data.
Future Work#
Future research directions stemming from this Nonlocal Attention Operator (NAO) paper could explore extending NAO’s capabilities to higher-dimensional systems, moving beyond the 2D examples presented. This would involve investigating efficient computational strategies for handling the increased complexity. A deeper theoretical analysis of the attention mechanism’s relationship to regularization in ill-posed inverse problems is warranted, potentially leading to more principled regularization techniques and improved generalization. Investigating NAO’s performance on a wider range of physical phenomena including fluid dynamics, quantum mechanics, and material science, would demonstrate its robustness and versatility. Furthermore, the paper highlights the potential for discovering hidden physical laws. Future work could focus on developing methods to automatically interpret and extract these laws from the learned kernel maps, enhancing the interpretability and practical utility of NAO. Finally, comparing NAO’s performance to other state-of-the-art methods on a standardized benchmark for physical system modeling would solidify its position within the field and guide future improvements.
More visual insights#
More on figures

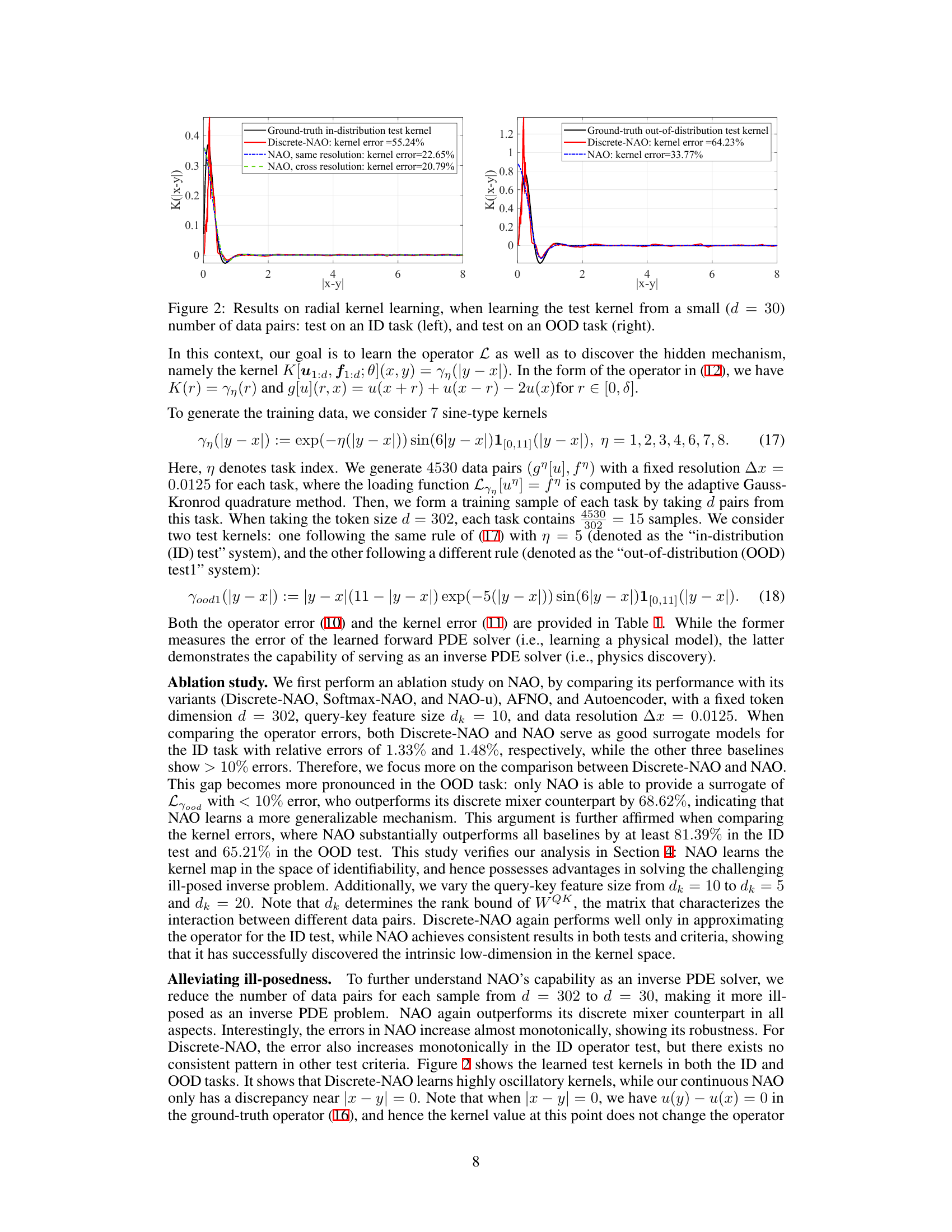
This figure displays the results of learning radial kernels with a small number of data pairs (d=30). The left panel shows the results for an in-distribution (ID) test, while the right panel shows the results for an out-of-distribution (OOD) test. The plots compare the learned kernels (from Discrete-NAO and NAO) against the ground truth. NAO demonstrates superior performance, particularly in the OOD task where it more accurately captures the true kernel’s shape. This highlights NAO’s ability to generalize to unseen data.

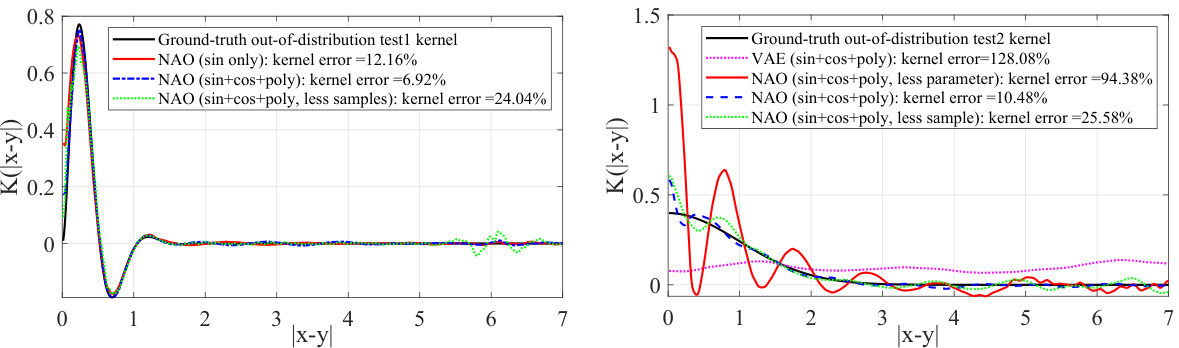
This figure compares the learned kernels from three different methods against the ground truth. The ground truth kernel represents the true inverse stiffness matrix. The kernel from Discrete-NAO shows significant artifacts and oscillations, highlighting its limitations. In contrast, the kernel learned using NAO is much closer to the ground truth, demonstrating its effectiveness in capturing the true underlying physics.

This figure visualizes the results of learning a heterogeneous material’s microstructure using the proposed Nonlocal Attention Operator (NAO). The top row displays the ground truth two-phase material microstructure, the input loading field, and the resulting pressure field. The bottom row shows the summation of the learned kernel (representing the material interaction), and the recovered microstructure after a thresholding step. The figure demonstrates the ability of NAO to uncover hidden physical properties from observed data, showcasing the power of the method for physics-informed learning.
This figure shows the results of learning radial kernels from a small dataset (d=30). The left panel displays the results for an in-distribution (ID) task, while the right panel shows the results for an out-of-distribution (OOD) task. The plots compare the ground truth kernels with those learned by Discrete-NAO and NAO, highlighting NAO’s superior performance, particularly in generalizing to unseen data.
More on tables

This table shows the performance of two models, Discrete-NAO and NAO, on two different tasks in solution operator learning: linear operator (g → p) and nonlinear operator (b → p). The results are presented for two different cases with varying numbers of samples and trainable parameters. The performance is measured by the test error, which is the percentage of error between the predicted and actual values. The table demonstrates that NAO performs better or comparably to Discrete-NAO in both tasks and cases, with fewer trainable parameters.

This table shows the results of applying NAO and Discrete-NAO to the heterogeneous material learning problem. Two cases are presented, one with fewer samples and smaller token size, and the other with more samples and larger token size. The table compares the ID (in-distribution) and OOD (out-of-distribution) test errors for both models, highlighting the performance differences between NAO and its discrete counterpart.

This table presents the results of experiments on radial kernel learning using different models (Discrete-NAO, Softmax-NAO, NAO, NAO-u, Autoencoder). It shows the test errors (operator and kernel) and the number of trainable parameters for each model under various conditions (different values of dk and data resolution). The results highlight the superior performance of NAO in addressing the ill-posed nature of the inverse problem and its ability to provide resolution-invariant estimators.
Full paper#