Autoregressive Image Generation without Vector Quantization

↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is highly important as it challenges the conventional wisdom in autoregressive image generation by eliminating the need for vector quantization. This opens exciting avenues for research, including faster and more efficient image generation models, and motivates the exploration of autoregressive models in other continuous-valued domains.

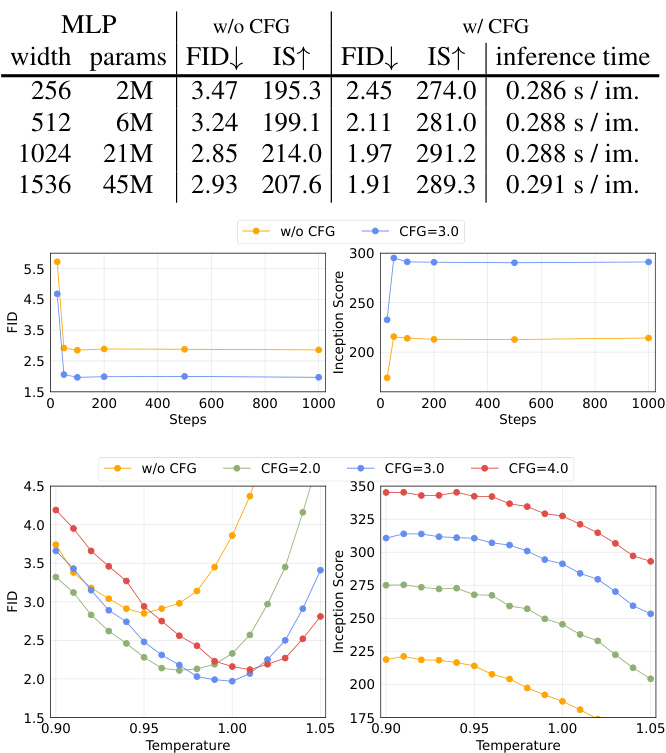
Visual Insights

#

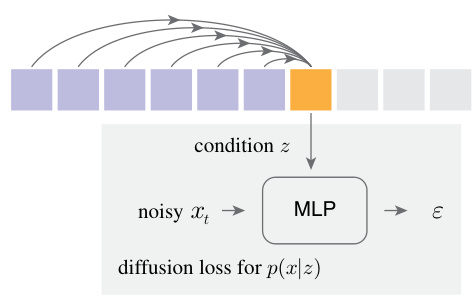
This figure illustrates the Diffusion Loss function. The autoregressive model generates a vector z conditioned on previous tokens. This vector z is then used as input to a small Multilayer Perceptron (MLP) along with a noisy version of the current token x_t. The MLP predicts the noise ε added to x_t, and the loss function measures the difference between the predicted noise and the actual noise. At inference time, this process is reversed to sample a new token from the learned distribution p(x|z). The key advantage is the elimination of the need for vector quantization.

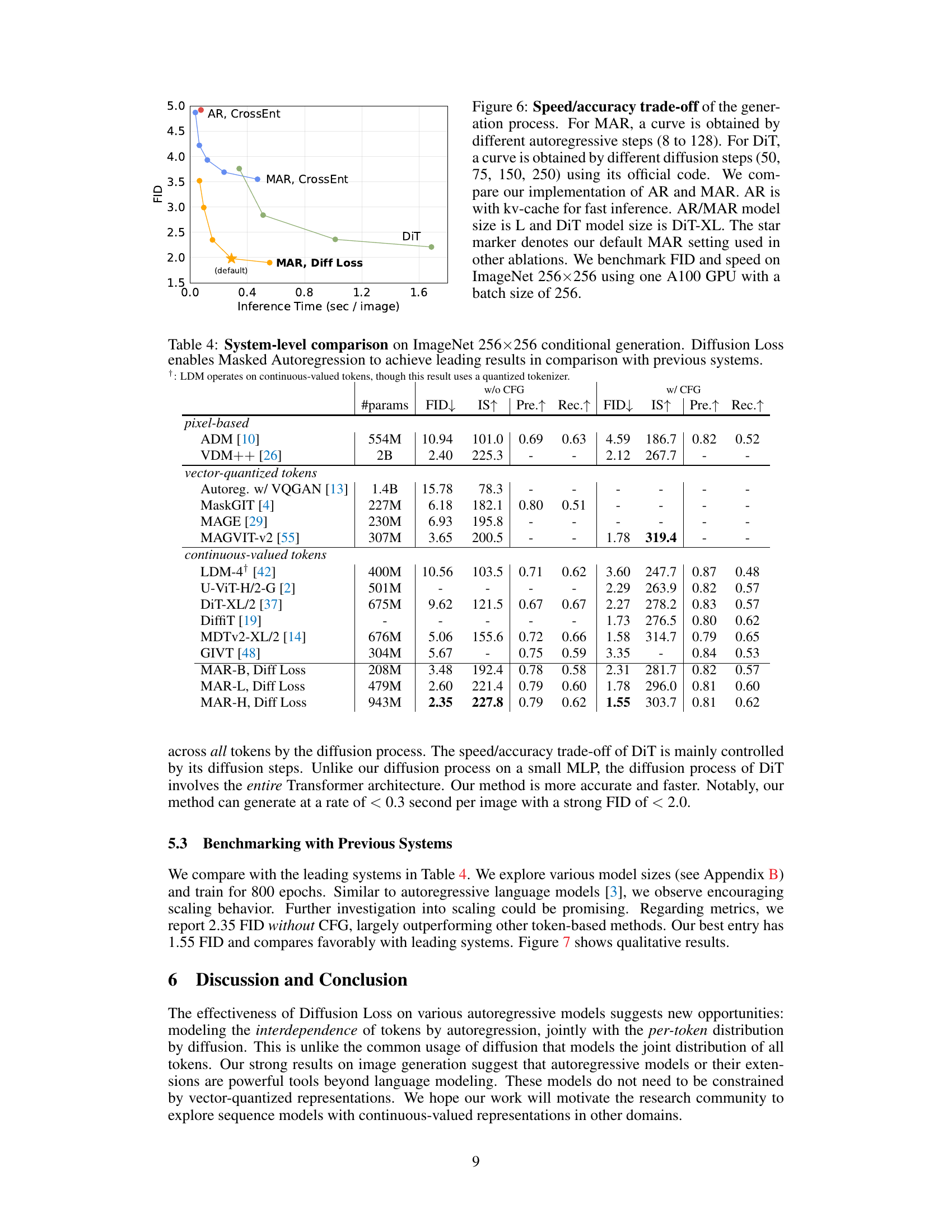
This table compares the performance of using Diffusion Loss with continuous tokens against Cross-entropy Loss with discrete tokens for various autoregressive (AR) and masked autoregressive (MAR) models. It shows that Diffusion Loss consistently outperforms Cross-entropy Loss across different model configurations, highlighting the benefits of using continuous tokens.

In-depth insights

#

VQ-free Autoregressive

#

The concept of “VQ-free Autoregressive” signifies a paradigm shift in autoregressive image generation models. Traditional approaches heavily rely on vector quantization (VQ) to discretize the continuous image space into a manageable set of discrete tokens. This VQ step, while enabling the use of efficient sequence models, introduces several limitations, including information loss due to quantization and potential quality degradation in reconstructed images. A VQ-free approach aims to bypass this step by directly modeling the continuous image space using a diffusion model. Diffusion models excel at representing complex probability distributions, making them well-suited for handling the rich and nuanced information within an image. This allows for autoregressive modeling without the constraints of VQ, potentially resulting in improved image quality and generation speed. While the elimination of VQ is the primary benefit, a VQ-free method would likely involve a more computationally expensive procedure during inference. Therefore, a successful VQ-free autoregressive system would need to carefully balance the trade-off between the quality enhancements and increased computational cost. This research direction is exciting because it has the potential to address longstanding challenges in autoregressive image synthesis.

Diffusion Loss

#

The proposed ‘Diffusion Loss’ offers a novel approach to autoregressive image generation by eliminating the need for vector quantization. Instead of relying on discrete tokens, it leverages the principles of diffusion models to directly model the per-token probability distribution in a continuous space. This is achieved by using the autoregressive model to predict a conditioning vector for each token, which then informs a small denoising diffusion network. The network’s output models the probability distribution of the continuous-valued token, allowing for sampling at inference time. This method’s strength lies in its flexibility and efficiency. It avoids the complexities and potential shortcomings of vector quantization, allowing autoregressive models to utilize higher-quality, non-quantized representations. Experimental results show strong performance, surpassing traditional methods using discrete tokens, showcasing the effectiveness of modeling the per-token probability with a diffusion procedure. The simplicity and effectiveness of ‘Diffusion Loss’ suggest its potential applicability to other continuous-valued domains.

MAR Model

#

The Masked Autoregressive (MAR) model, a key contribution of this research, presents a novel approach to autoregressive image generation. Instead of sequentially predicting tokens one at a time, as in standard autoregressive models, MAR predicts multiple tokens simultaneously in a randomized order. This strategy is conceptually similar to masked image modeling techniques. This approach is particularly efficient because it reduces the number of sequential prediction steps required, thereby significantly accelerating the generation process. Furthermore, MAR is shown to be highly flexible and adaptable to diverse continuous-valued tokenizers, a notable improvement over the limitations of traditional discrete-valued tokenizers frequently used in autoregressive image generation. The combination of masked prediction with continuous-valued tokens via Diffusion Loss proves remarkably effective in eliminating the need for quantization and boosting generation quality. This is a crucial advancement as it addresses the longstanding constraint of autoregressive models being inherently linked to discrete representations, effectively opening up new avenues for continuous data modeling in this domain.

Ablation Studies

#

Ablation studies systematically remove components of a model or method to assess their individual contribution. In the context of a research paper on autoregressive image generation, an ablation study might investigate the impact of removing different model features, such as the diffusion loss function or the type of attention mechanism (e.g., causal vs. bidirectional). By comparing the performance of the full model to variants with specific components removed, researchers can isolate the effects of each part and quantify its importance. Results from an ablation study would often demonstrate if the contributions are additive or synergistic, providing critical insights into the model’s design. A well-designed ablation study is essential to verify the effectiveness of individual components, as it demonstrates if each contribution is crucial for the model’s performance. Furthermore, ablation studies can guide future model improvements, identifying areas for further development or modification. The results often highlight which elements are most important for overall success and can point out potentially unnecessary parts that might improve efficiency if removed.

Future Works

#

Future work in this area could explore several promising directions. Extending the approach to other continuous-valued domains beyond image generation is crucial, testing its efficacy in areas such as audio synthesis or 3D model generation. Investigating alternative diffusion models and exploring the synergy between autoregressive modeling and different diffusion strategies would significantly advance performance. Analyzing the impact of various tokenizers and architectures on overall quality and efficiency is essential for optimizing the model’s performance. Finally, addressing limitations in handling long-range dependencies within autoregressive frameworks and improving the model’s robustness to noisy or incomplete inputs will pave the way towards more sophisticated and reliable autoregressive generative models. These improvements, along with the proposed methodology, will propel the field forward.

More visual insights

#

More on figures

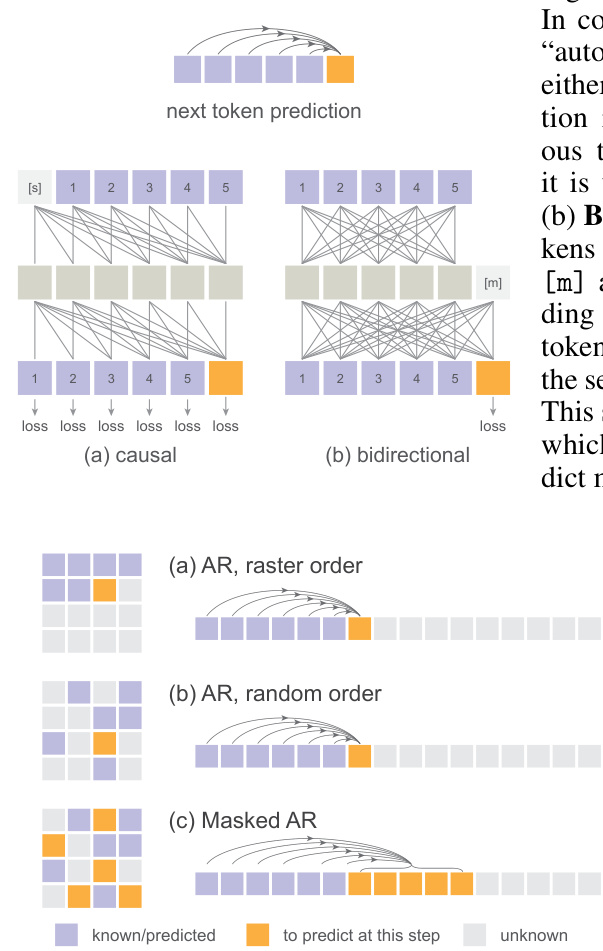
This figure compares causal and bidirectional self-attention mechanisms in autoregressive models for image generation. Causal attention limits each token’s attention to previous tokens, while bidirectional attention allows tokens to attend to all other tokens. This is exemplified in the context of standard, raster-ordered autoregressive models and masked autoregressive (MAR) models, demonstrating how bidirectional attention facilitates both standard and masked autoregressive generation.

This figure illustrates the core concept of Diffusion Loss, a novel loss function proposed in the paper. It shows how an autoregressive model generates a conditioning vector (z) for a continuous-valued token (x). This vector then serves as input to a small Multi-Layer Perceptron (MLP) which models the probability distribution p(x|z). The MLP is trained together with the autoregressive model. During inference, this allows for sampling a token from p(x|z) without using vector quantization.

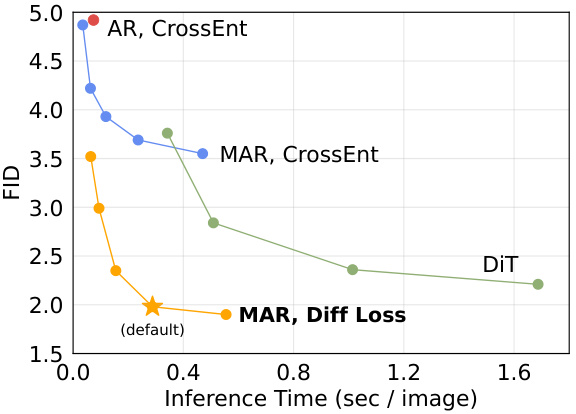
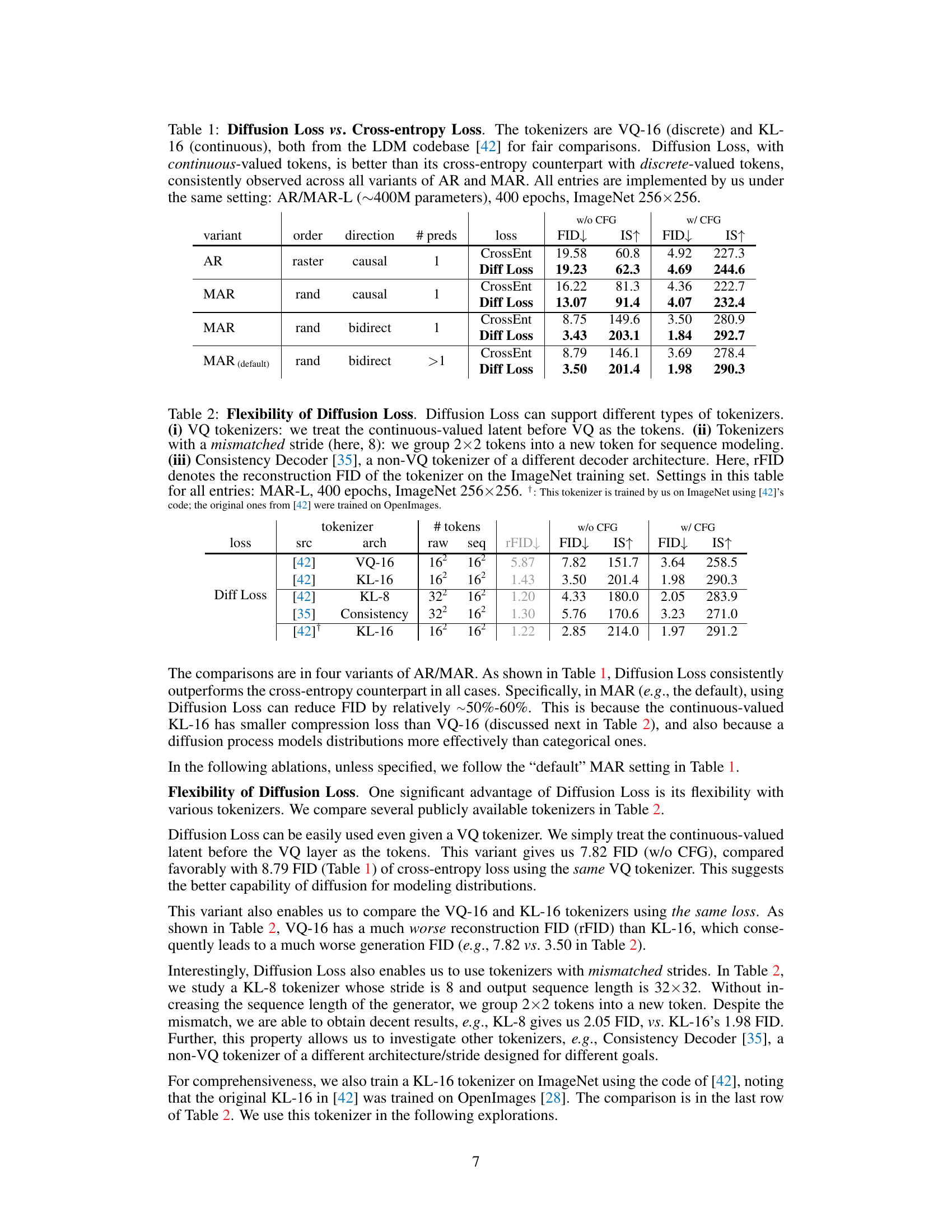
This figure shows the trade-off between speed and accuracy (FID score) for different image generation models. The x-axis represents inference time per image, and the y-axis represents the FID score, a measure of image quality. Three models are compared: a standard autoregressive model (AR), a masked autoregressive model (MAR) with cross-entropy loss, and the same MAR model but using the proposed Diffusion Loss. Each model’s performance is shown as a curve representing different generation steps or diffusion steps to demonstrate the trade-off. The star marks the default setting used for the MAR model with Diffusion Loss in other experiments, highlighting its superior speed/accuracy balance.

This figure displays a diverse set of images generated by the MAR-H model (masked autoregressive model with the largest architecture) utilizing the Diffusion Loss function. The images demonstrate the model’s ability to generate high-quality, class-conditional images across various categories from ImageNet.

This figure shows a comparison of the image generation results between the proposed MAR-H model and the DiT-XL model. Each pair of images shows results for the same class from both models, illustrating that both models can generate images with artifacts, despite their differences in approach.

This figure compares causal and bidirectional attention mechanisms in autoregressive models. Causal attention, used in standard autoregressive models, processes tokens sequentially, with each token only attending to preceding tokens. Bidirectional attention, however, allows tokens to attend to all other tokens, potentially enabling better information flow and faster generation. The figure highlights how bidirectional attention can still function as autoregressive (predicting the next token), and further allows simultaneous prediction of multiple tokens.

More on tables

This table demonstrates the flexibility of the proposed Diffusion Loss by showcasing its compatibility with various tokenizers, including VQ tokenizers, tokenizers with mismatched strides, and non-VQ tokenizers. It compares the performance (FID and IS scores) across different tokenizer types on the ImageNet dataset, highlighting the robustness and adaptability of the Diffusion Loss.

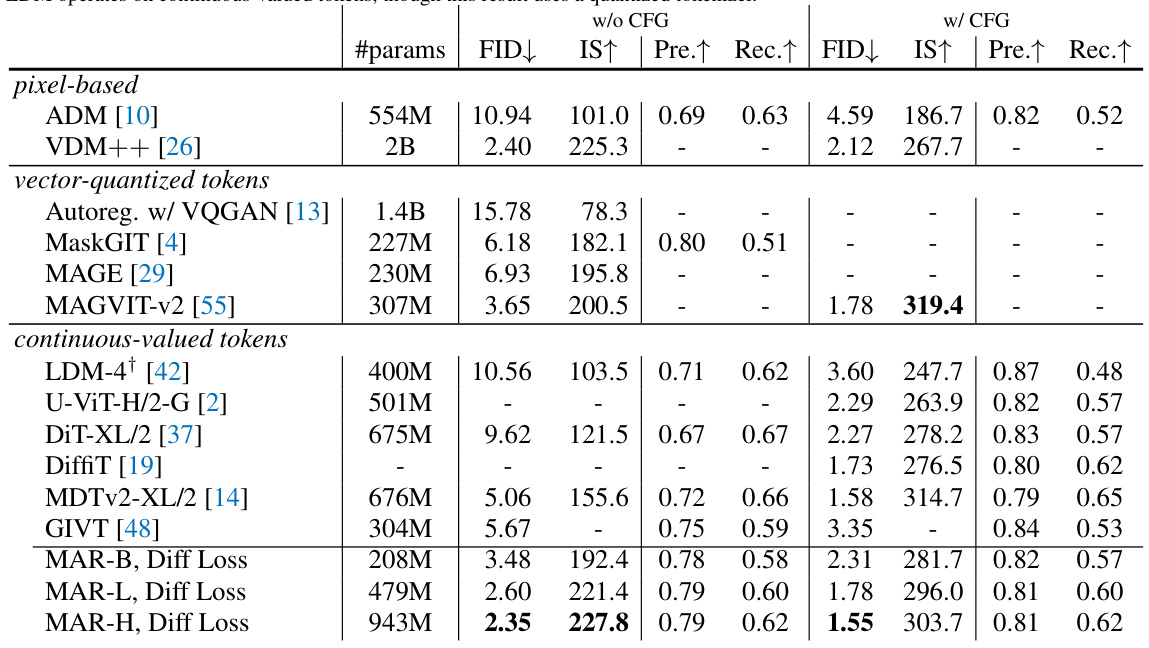
This table compares the performance of using Diffusion Loss with continuous-valued tokens against the standard cross-entropy loss with discrete-valued tokens. The comparison is performed across various autoregressive (AR) and masked autoregressive (MAR) model configurations, using the same hyperparameters and dataset (ImageNet 256x256). The results show that Diffusion Loss consistently outperforms cross-entropy loss, highlighting the benefits of using continuous tokens.

This table demonstrates the flexibility of the proposed Diffusion Loss by showing its effectiveness with various types of tokenizers, including VQ tokenizers, tokenizers with mismatched strides, and a non-VQ tokenizer called Consistency Decoder. The results highlight that Diffusion Loss is not limited to specific types of tokenizers and can adapt to different scenarios, providing consistent performance gains.

This table compares the performance of the proposed Diffusion Loss with the traditional cross-entropy loss using different autoregressive (AR) and masked autoregressive (MAR) models. Two types of tokenizers, VQ-16 (discrete) and KL-16 (continuous), are used for a fair comparison. The results show that Diffusion Loss consistently outperforms cross-entropy loss across various model configurations, highlighting its effectiveness in image generation.

Full paper

#