↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Deep predictive models have revolutionized neuroscience, but their high overparameterization leads to inconsistent results across different model runs. This paper focuses on improving the reproducibility and consistency of neuronal embeddings obtained from these models, which are essential for meaningful downstream analyses, such as defining functional cell types.
The researchers address this by introducing an adaptive L1 regularization technique that adjusts the regularization strength per neuron, significantly improving both predictive performance and the consistency of neuronal embeddings. Furthermore, they propose an iterative feature pruning strategy to reduce model complexity without losing predictive power, thus enhancing reproducibility. The findings reveal that improved identifiability is crucial for building objective taxonomies of cell types and achieving compact representations of functional landscapes. This work highlights the importance of addressing overparametrization and improving model identifiability for reliable and robust deep learning models in neuroscience.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with deep predictive models of neural activity. It directly addresses the reproducibility problem, a critical concern in AI and neuroscience, offering methods to improve the consistency of learned embeddings and the generalizability of findings. Its iterative feature pruning strategy and adaptive regularization technique are significant contributions with broader implications for machine learning model interpretability and efficiency.
Visual Insights#

The figure illustrates the model architecture, readout alignment, and analysis pipeline. Panel A shows the core (shared feature representation) and readout (neuron-specific weights) components of the deep neural network model used. Two types of readouts are detailed: Factorized readout and Gaussian readout. Panel B illustrates the alignment process of embedding vectors to obtain rotation invariance. Panel C outlines the overall data processing pipeline: model training, embedding alignment, clustering, and adjusted Rand index (ARI) calculation for evaluating embedding consistency.
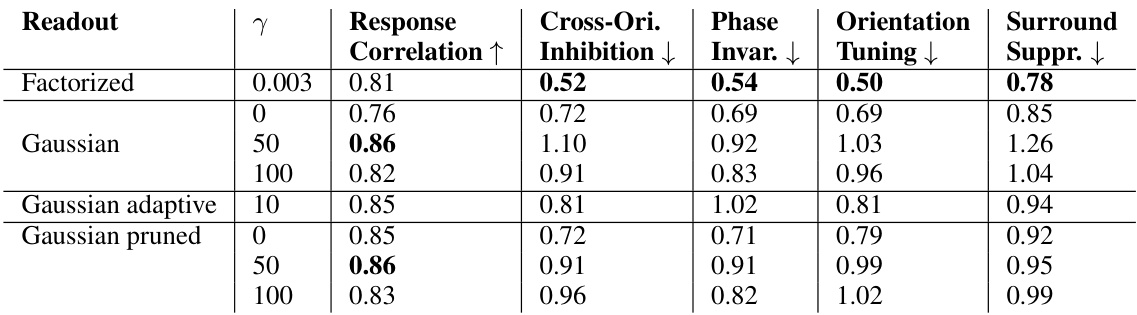
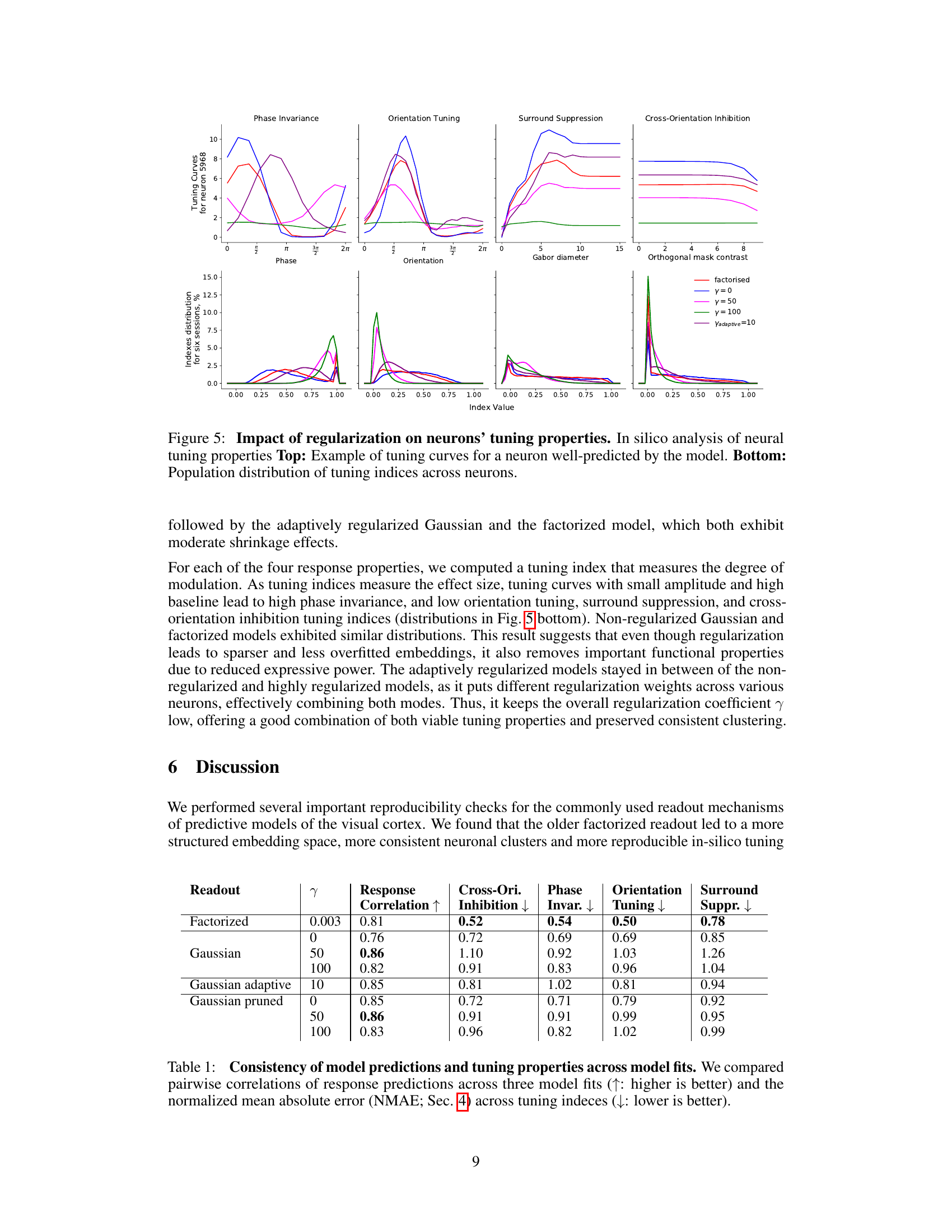
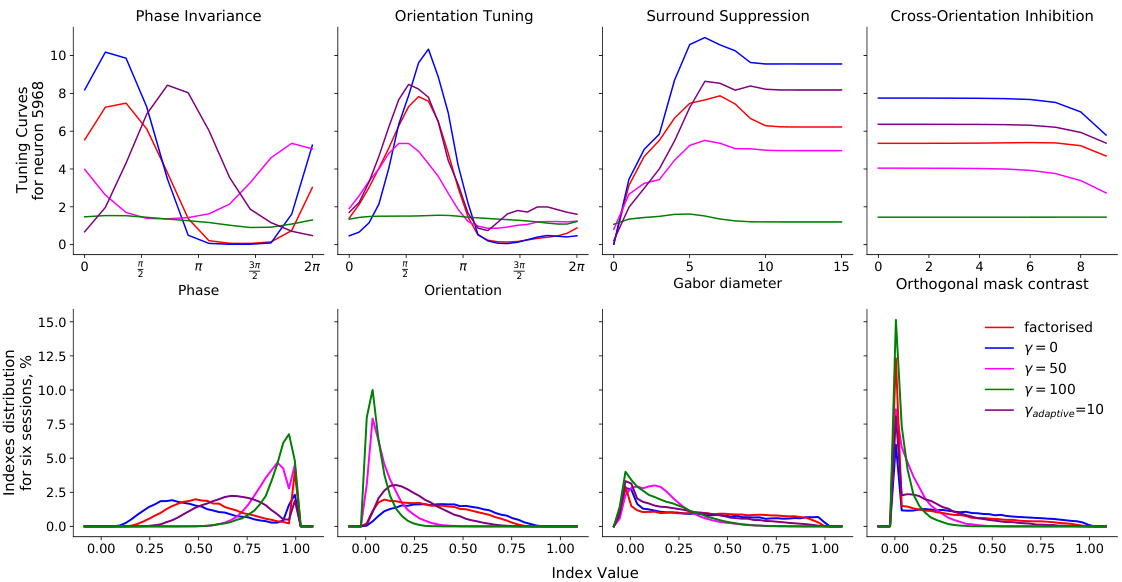
This table presents a comparison of the consistency of model predictions and neuronal tuning properties across different model architectures and regularization schemes. It shows the Pearson correlation of predicted vs. observed neuronal responses, and the normalized mean absolute error (NMAE) for four key tuning properties: cross-orientation inhibition, phase invariance, orientation tuning, and surround suppression. Higher correlation indicates better predictive performance, while lower NMAE signifies greater consistency across model fits. The table allows for a quantitative comparison of the models’ ability to reproduce both response patterns and known neuronal tuning characteristics.
In-depth insights#
Predictive Model Stability#
Predictive model stability is crucial for reliable scientific conclusions, particularly in neuroscience where deep learning models are increasingly used to model complex neural systems. The core issue is the reproducibility of model-generated neuronal embeddings, which represent the functional properties of neurons and often serve as the basis for downstream analysis, such as cell-type classification. The challenge is that deep learning models tend to be overparameterized, leading to multiple equivalent solutions and making the model fits unstable across different initialization seeds or model architectures. The paper investigates this instability by assessing the consistency of neuronal embeddings across multiple model training runs, varying the regularization and pruning strategies. Results show that L1 regularization improves the consistency and structure of embeddings, and that an adaptive regularization scheme further enhances this, while retaining predictive performance. Furthermore, iterative feature pruning reduces model complexity without sacrificing performance and improving embedding consistency. The study highlights the need for novel architectures or learning techniques that enhance the identifiability of neuronal representations to achieve a more objective taxonomy of cell types.
L1 Regularization Effects#
The study investigates the impact of L1 regularization on the reproducibility of predictive models for neuronal activity in the mouse visual cortex. L1 regularization, by enforcing sparsity in the model’s weights, is found to be crucial for obtaining structured neuronal embeddings, which are representations of neuron function used for downstream analysis. Applying L1 regularization uniformly across all neurons, however, does not consistently improve clustering of embeddings across multiple model runs, indicating a need for a more refined approach. The authors introduce an adaptive regularization technique that dynamically adjusts the regularization strength per neuron, leading to more consistent and structured embeddings while preserving predictive performance. This highlights the importance of tailoring regularization to individual neuronal characteristics, rather than imposing a global constraint. Further enhancing reproducibility, the authors explore an iterative feature pruning strategy, which successfully reduces the model’s complexity without affecting predictive accuracy and improves the consistency of the embeddings. This emphasizes that overparametrization in deep learning models can hinder reproducibility and that techniques to manage model complexity are essential for achieving robust and reliable results in neuroscience modeling.
Adaptive Regularization#
The core idea behind adaptive regularization is to dynamically adjust the regularization strength for each neuron in a neural network, rather than applying a uniform penalty across all neurons. This addresses the issue of overparameterization in deep predictive models, which can lead to inconsistent neuronal embeddings across different model fits. Inconsistent embeddings hinder the reliable identification of neuronal cell types via clustering. The authors propose an adaptive scheme where the regularization strength is controlled by a learnable parameter for each neuron, subject to a log-normal hyperprior. This approach allows the model to focus regularization on neurons that need it most, while allowing others more freedom. The results demonstrate that this adaptive strategy effectively improves the consistency of neuronal embeddings across model fits compared to traditional uniform regularization, thereby leading to a more robust and objective taxonomy of cell types. The method maintains near state-of-the-art predictive performance, showcasing a successful balance between model regularization and preservation of biological relevance.
Network Pruning Impact#
The study investigates the impact of network pruning on the reproducibility of predictive models for mouse visual cortex. Over-parameterization in deep neural networks is identified as a key challenge to reproducibility, with multiple models achieving similar performance but yielding inconsistent neuronal embeddings. The authors explore an iterative feature pruning strategy, demonstrating that dimensionality reduction by half is possible without loss of predictive accuracy. This pruning improves the consistency of neuronal embeddings across model runs, enhancing the stability of downstream clustering analysis aimed at classifying neuronal cell types. While pruning improves consistency, the study also highlights the trade-off between performance and embedding consistency, and suggests that further work is needed to develop architectures that achieve both high performance and high identifiability of neuronal cell types.
Tuning Index Consistency#
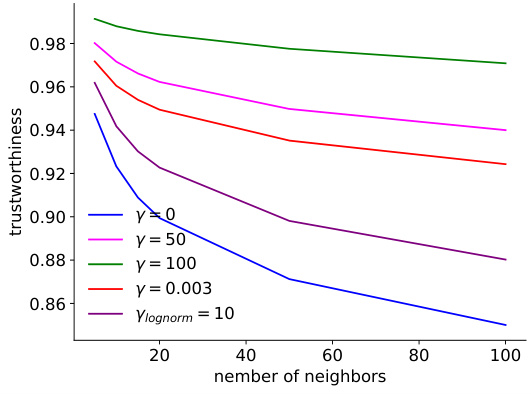
The concept of “Tuning Index Consistency” in the context of a neuroscience research paper likely refers to how reliably a model’s predictions of neuronal tuning properties (e.g., orientation selectivity, spatial frequency preference) align across different model runs. High consistency indicates that the model consistently assigns similar functional characteristics to the same neurons, regardless of random variations in initialization or training. Low consistency suggests that the model’s output is highly sensitive to these random factors, indicating a lack of robustness and potentially hindering the reliability of its insights into neuronal organization. Analyzing tuning index consistency is crucial for assessing the model’s ability to accurately and reliably capture neuronal function. A high degree of consistency strengthens the confidence in the model’s ability to objectively classify neuron types or create a compact representation of the functional landscape, while low consistency raises concerns about the model’s reliability and generalizability, potentially indicating overparameterization or a need for improved model architecture or training techniques. Inconsistencies could arise from overparameterization in deep neural networks, leading to multiple similar solutions but with differing embedding representations, highlighting the importance of regularization or other strategies to enhance model identifiability and enhance the stability of neuronal embeddings across model runs.
More visual insights#
More on figures
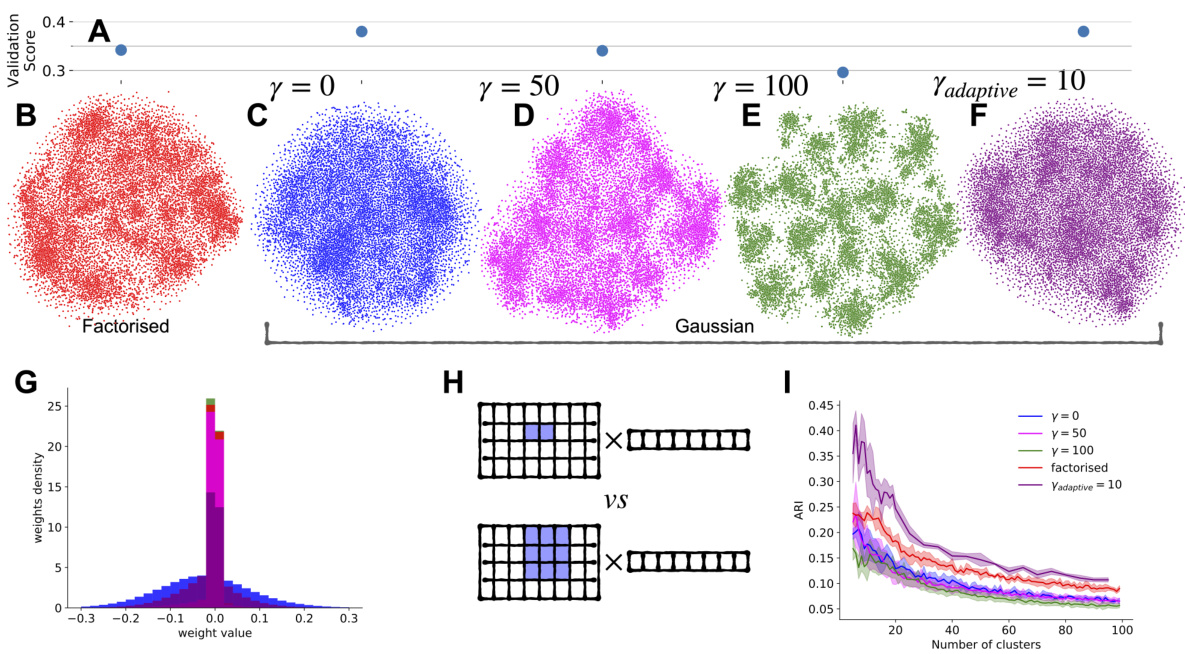
Figure 2 displays the impact of different regularization strengths on the performance and consistency of neuronal embeddings across various model architectures (factorized and Gaussian readouts). It demonstrates that adaptive regularization offers a balance between predictive performance and consistent clustering of embeddings, outperforming both factorized and uniformly regularized models. The figure shows the performance, t-SNE projections of embeddings, weight distribution histograms, an example of adaptive regularization, and ARI scores for clustering across different models and regularization schemes.

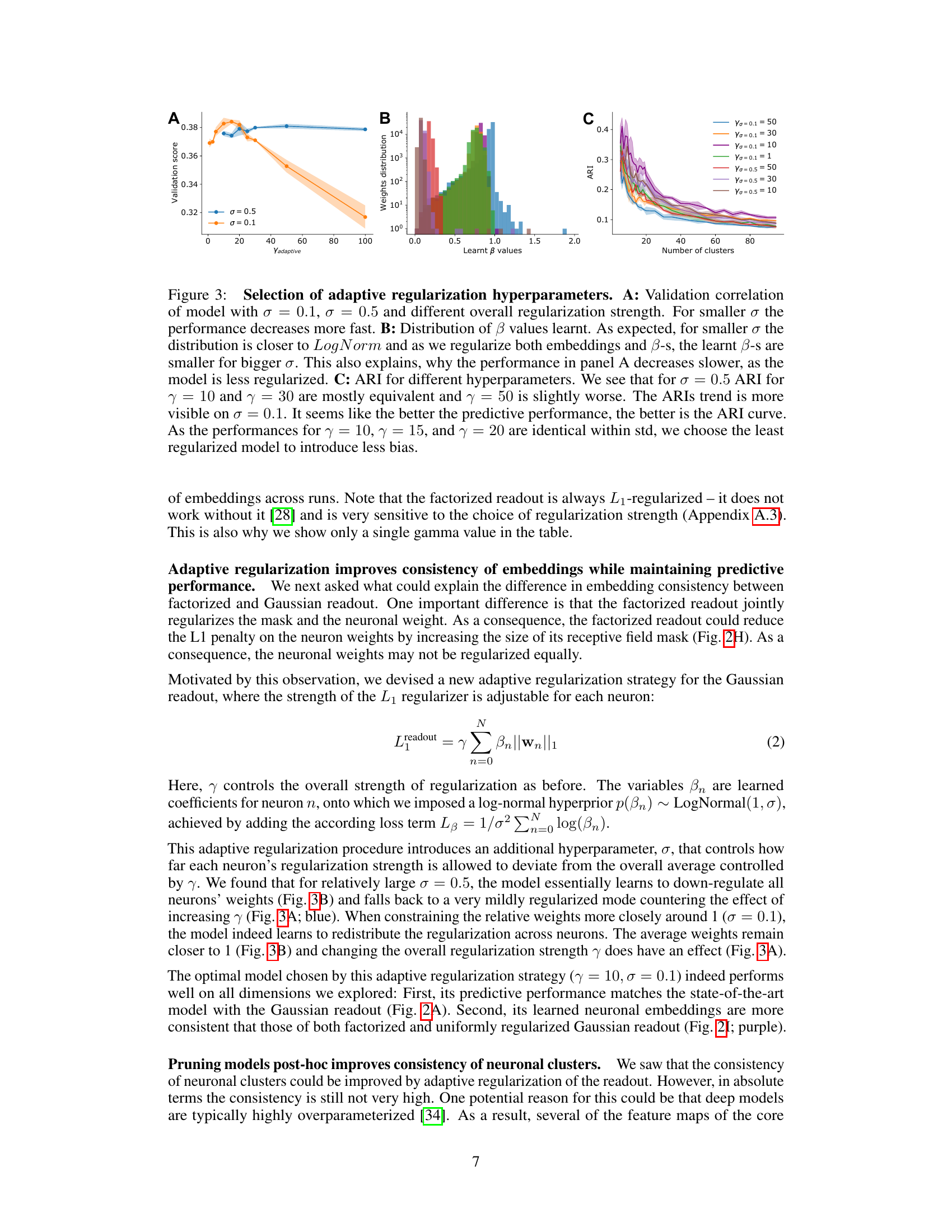
This figure displays the results of experiments on selecting optimal hyperparameters for adaptive regularization. Panel A shows the validation correlation for different overall regularization strengths (γ) and standard deviations (σ) of the log-normal prior on neuron-specific regularization coefficients (β). Panel B presents the distribution of the learned β values for various combinations of γ and σ. Panel C illustrates the adjusted Rand index (ARI) for different hyperparameter settings across various numbers of clusters, indicating the impact of these choices on the consistency of neuronal embeddings. The results indicate the effectiveness of adaptive regularization in balancing prediction performance and embedding consistency.
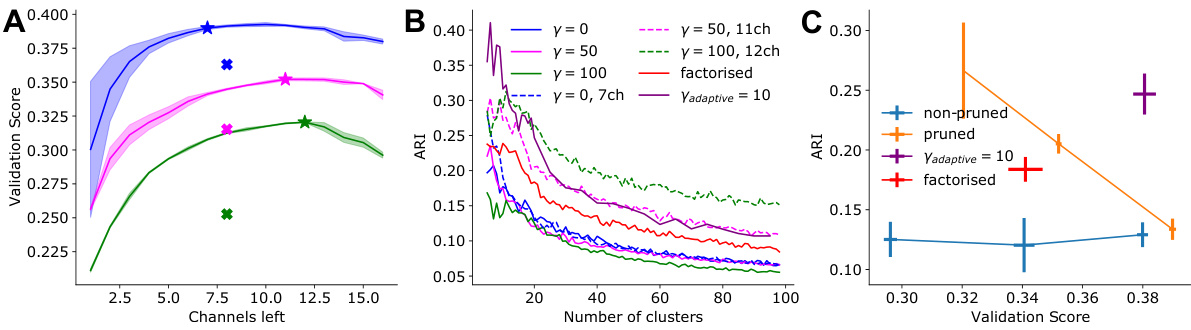
This figure shows the effect of pruning on model performance and consistency of neuronal embeddings. Panel A displays the validation score of pruned models with different regularization methods, showing that pruning can improve performance while maintaining consistency in clustering. Panel B illustrates how ARI, a measure of consistency in clustering, increases with pruning, indicating that removing less important features enhances the robustness of the embeddings. Panel C presents the trade-off between ARI and validation score, highlighting the best model that balances both measures. The adaptive regularization readout pruning method is a key innovation that improves the balance between performance and consistency.
This figure displays the results of an experiment comparing different model architectures and regularization techniques for predicting neuronal activity in the visual cortex. Panel A shows the correlation between predicted and observed neural responses, indicating model performance. Panels B-F show t-SNE projections of the learned neuronal embeddings under different regularization strengths, visualizing the structure of the embedding space. Panel G compares the weight distributions for different models. Panel H illustrates the concept of adaptive regularization, demonstrating how it adjusts the regularization strength based on learned receptive field masks and embedding sparsity. Finally, Panel I depicts the adjusted Rand index (ARI) for clustering the embeddings, measuring the consistency of the results across different model fits and random seeds.
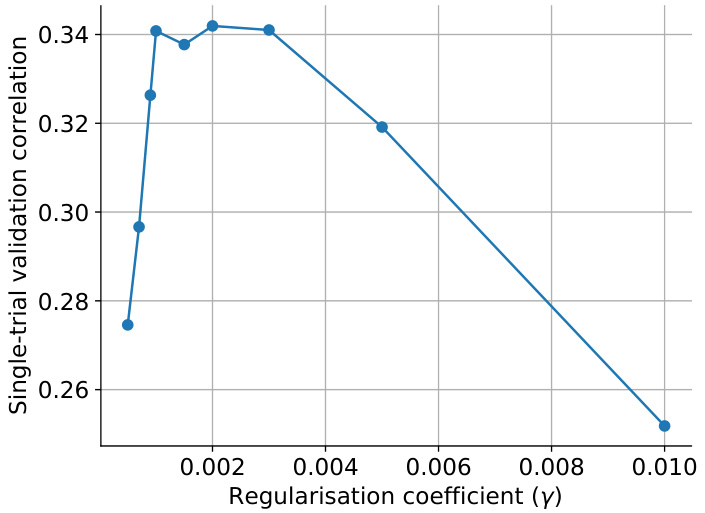
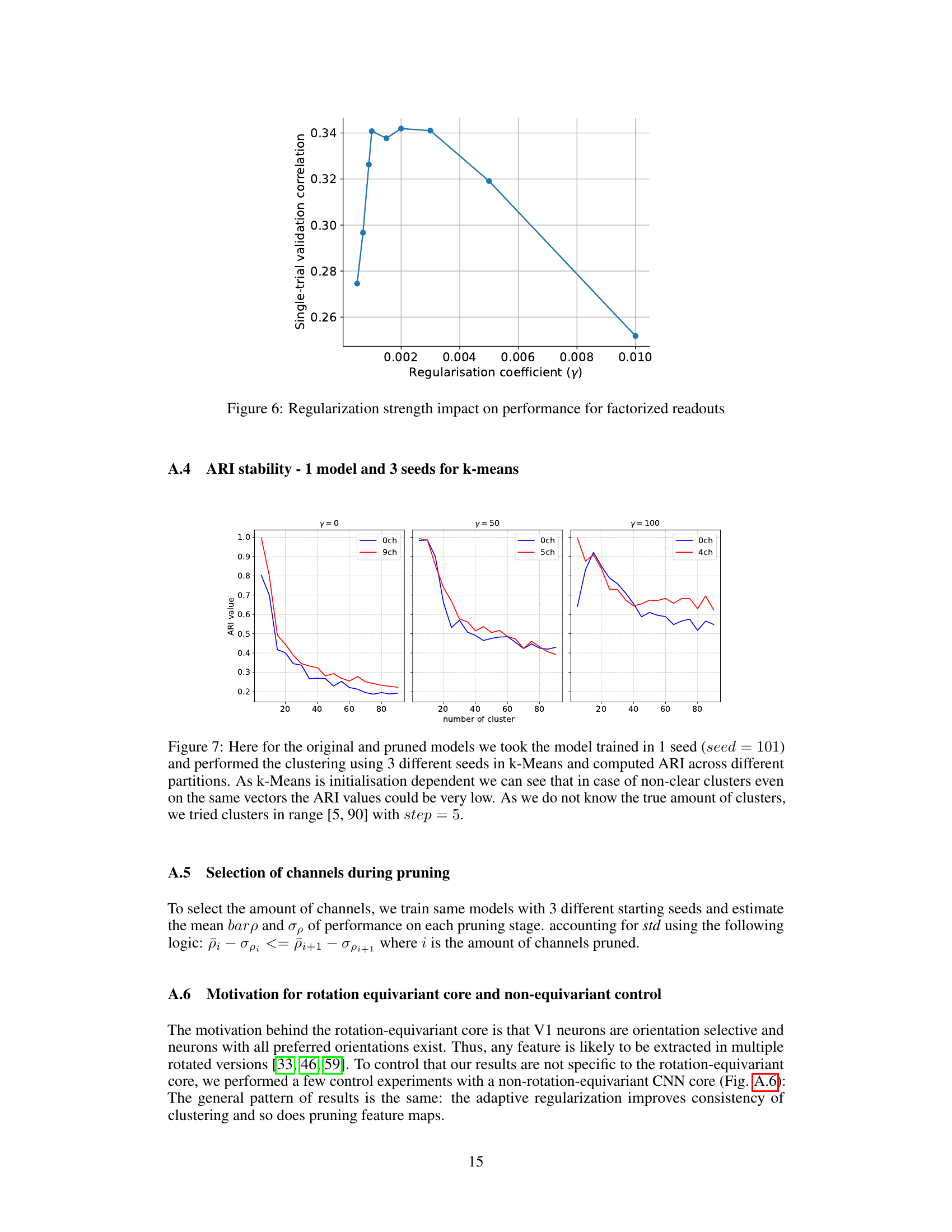
This figure shows the impact of the regularization strength (gamma, γ) on the single-trial validation correlation for factorized readouts. The x-axis represents the regularization coefficient (γ), and the y-axis represents the single-trial validation correlation. The plot shows that there is an optimal regularization strength that maximizes the validation correlation. Too little or too much regularization hurts performance. The optimal value seems to be around 0.003.
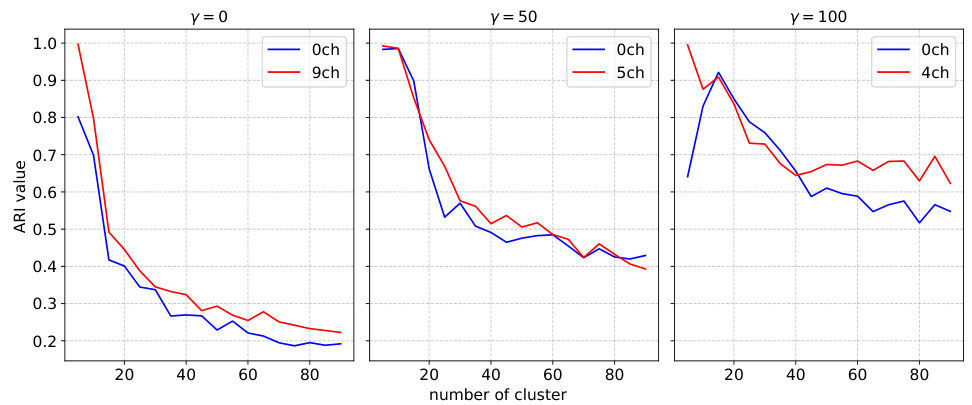
Figure 2 displays the results of the experiments comparing different regularization strategies for the factorized and Gaussian readouts. Panel A shows model performance. Panels B-F show the t-SNE projections of the embeddings for different regularization strengths (gamma values). Panel G compares weight distributions before alignment. Panel H illustrates the adaptive regularization scheme, showing how the mask and embedding are regularized differently based on the learned receptive field size. Panel I shows the ARI scores for different regularization and clustering approaches.
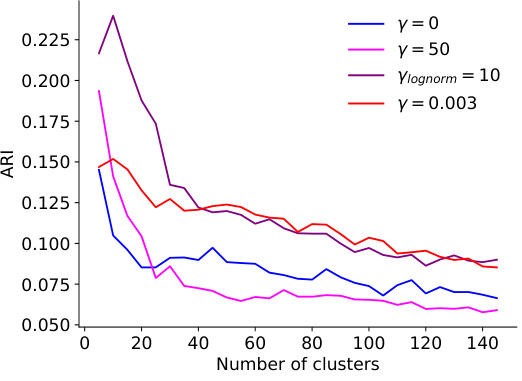
Figure 2 displays the results of an experiment that explores the impact of different regularization techniques on the quality of neuronal embeddings. Panel A shows a comparison of the performance of different model types (factorized vs. Gaussian readout) in terms of correlation between predicted and observed neuronal activity. Panels B-F illustrate the impact of varying the strength of L1 regularization on the resulting embeddings, visualized using t-SNE. Panel G provides a detailed look at the distribution of weights before any alignment, comparing the effects of different regularization methods. Panel H offers a visual explanation of the adaptive regularization strategy used for the factorized mask, illustrating how it adjusts the level of regularization per neuron.
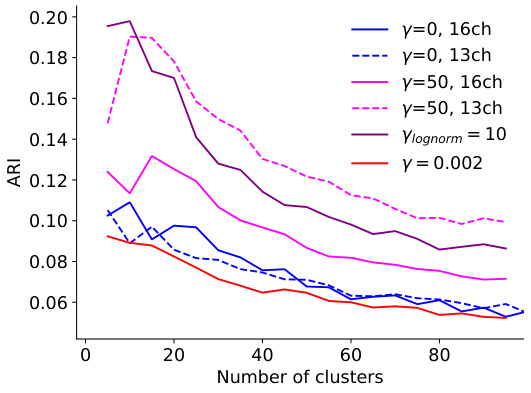
Figure 2 shows the impact of different regularization techniques on the quality of neuronal embeddings obtained from predictive models of the visual cortex. Panels A-F visualize model performance, embedding projections using t-SNE, weight histograms, an example of adaptive regularization, and adjusted Rand index (ARI) results across various regularization strengths. The results highlight the importance of L1 regularization for obtaining structured embeddings and the benefits of an adaptive regularization scheme that improves embedding consistency for downstream analyses.

This figure displays the optimal Gabor filters selected by the model for different regularization strengths (gamma=0, 50, 100) and three different random seeds. Each column represents a neuron and each row shows the optimal Gabor for a specific regularization strength and seed. The results suggest a degree of consistency in the selection of optimal Gabor filters across different runs, with more regularized models tending to select smaller Gabor filters.

This figure shows the optimal Gabor filters selected by the model for different neurons and training conditions. Each column represents a single neuron, each row shows the optimal Gabor filter obtained under different regularization strength and random seed. The figure shows that there is some consistency in Gabor filter selection across training conditions, but the selection isn’t always identical.
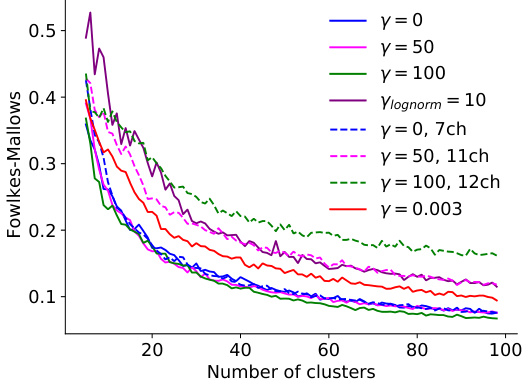
Figure 2 shows the effects of different regularization strengths on the performance and consistency of neuronal embeddings across different model fits. It includes visualizations of embeddings using t-SNE, histograms of weights, an example of adaptive regularization, and the adjusted Rand Index (ARI) for evaluating clustering consistency. The results highlight the importance of L1 regularization for obtaining well-structured embeddings and the benefits of an adaptive regularization scheme.

This figure shows the results of different regularization methods applied to the model for predicting neuronal activity in the visual cortex. Panels A-F demonstrate the effect of regularization strength on the model’s performance and the clustering of neuronal embeddings. Panel G shows the distribution of weights before and after alignment, while panel H illustrates the adaptive regularization scheme. Finally, panel I presents the adjusted rand index (ARI) values, quantifying the consistency of neuron clustering across multiple model fits. It aims to explore the effect of different regularization approaches on the consistency of neuron representations and clustering results.
This figure displays the results of an experiment comparing different regularization techniques on a model of neuronal activity. It shows model performance (correlation between predicted and observed neuronal responses), t-SNE projections of neuronal embeddings, weight distribution histograms, an example of adaptive regularization, and adjusted Rand Index (ARI) values for clustering embeddings across different models. The results demonstrate that L1 regularization is important for obtaining structured embeddings and that an adaptive regularization scheme improves consistency.

Figure 2 shows the results of an experiment comparing different regularization methods applied to predictive models of neuronal activity. Panel A shows the performance of the models, measured by the correlation between predicted and observed neuronal responses. Panels B-F display t-SNE projections of the learned neuronal embeddings obtained from models with different regularization strengths. Panel G provides a histogram of the weights from different models, demonstrating the impact of regularization on the sparsity of the weight distribution. Panel H illustrates the mechanism of adaptive regularization, which adjusts the regularization strength per neuron based on the learned mask size. Finally, Panel I shows the adjusted rand index (ARI) obtained by clustering the neuronal embeddings across different models and regularization schemes.
Full paper#