Breaking Long-Tailed Learning Bottlenecks: A Controllable Paradigm with Hypernetwork-Generated Diverse Experts

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel, controllable paradigm for long-tailed learning, addressing the limitations of existing methods. It offers flexible control over the trade-off between head and tail classes, allowing adaptation to diverse real-world scenarios and user preferences. This work opens up new avenues for research in handling distribution shifts and personalized long-tailed learning, with significant implications for various applications.

Visual Insights

#

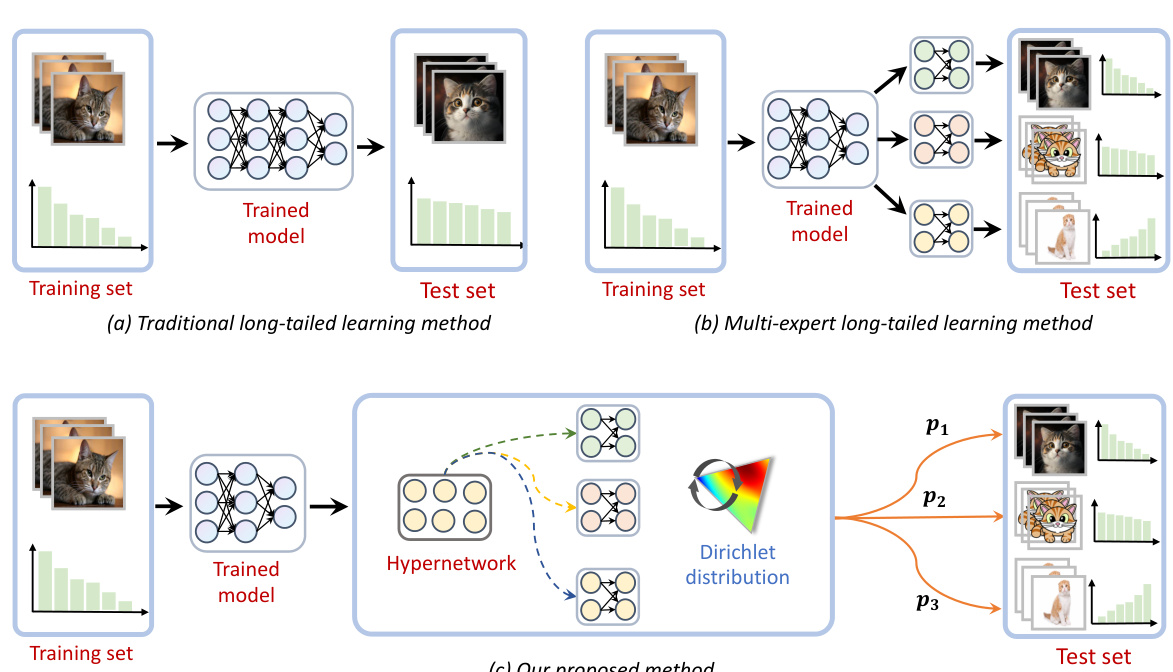
This figure compares three different approaches to long-tailed learning. (a) shows the traditional approach where a single model is trained on the imbalanced dataset, often resulting in poor performance on tail classes during testing with different distributions. (b) illustrates a multi-expert approach where multiple experts are trained on different distributions from the same dataset, but still lacks flexibility to adapt to arbitrary test-time distributions. (c) presents the proposed method which samples diverse preference vectors during training to generate a diverse set of expert models via hypernetworks to address any possible distribution scenarios. The ensemble model is optimized to flexibly adapt to any test distribution and output a dedicated model solution according to the user’s preference.

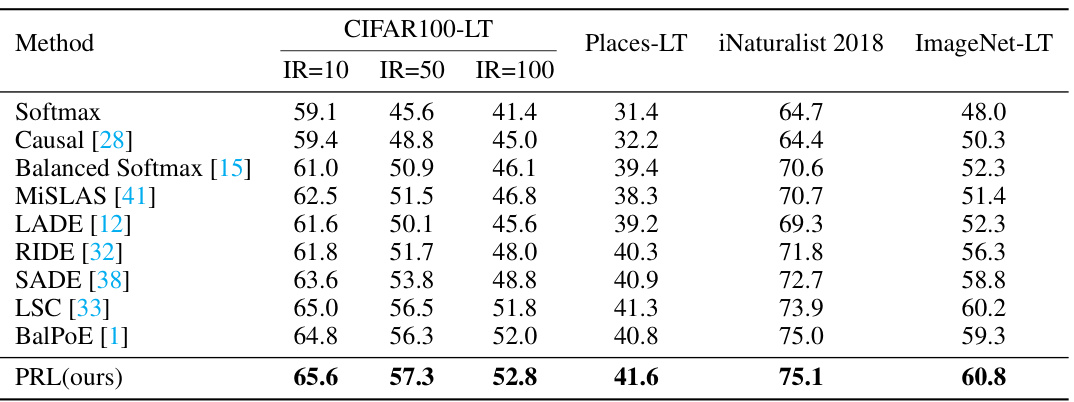
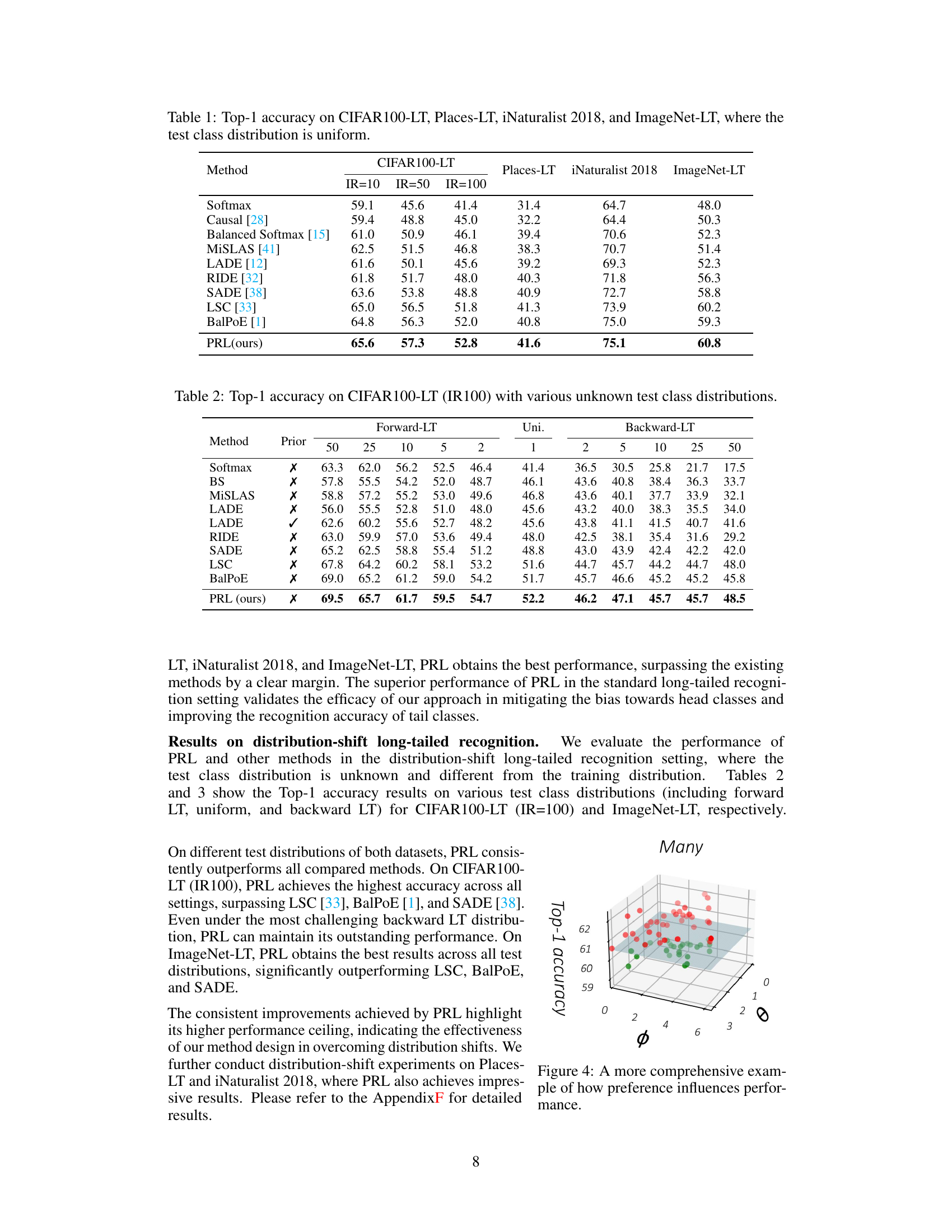
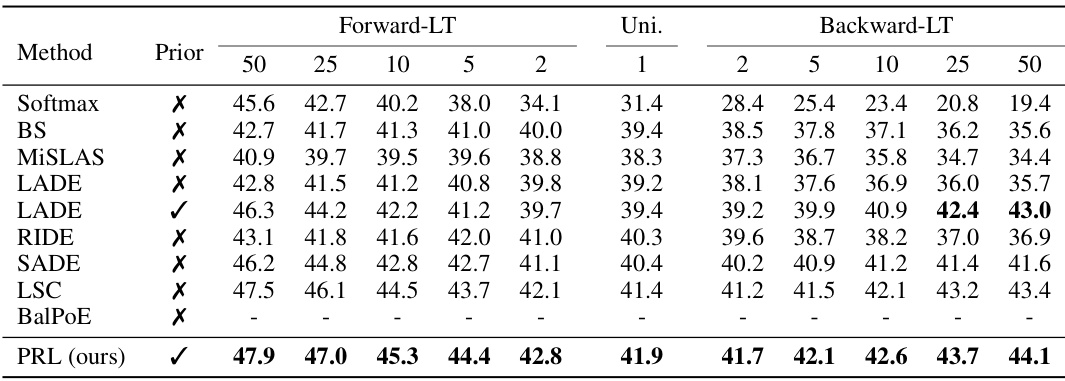
This table presents the top-1 accuracy results achieved by various long-tailed recognition methods on four benchmark datasets (CIFAR100-LT, Places-LT, iNaturalist 2018, and ImageNet-LT). The key aspect is that the test data distribution is uniform, meaning the class balance is even during testing, in contrast to the imbalanced training data. This allows for a comparison of how well different methods can generalize to balanced data after training on long-tailed data. The table shows the performance of each method across different imbalance ratios in CIFAR100-LT (IR=10, IR=50, IR=100) and the overall accuracy for Places-LT, iNaturalist 2018, and ImageNet-LT.

In-depth insights

#

Long-Tail Learning

#

Long-tail learning tackles the challenge of highly imbalanced datasets, where a few classes (head) dominate while many classes (tail) have scarce data. Traditional machine learning methods struggle with this imbalance, often neglecting the under-represented tail classes and resulting in poor performance. Addressing this requires specialized techniques that focus on balancing the class distribution, such as oversampling minority classes, modifying loss functions to weigh tail classes more heavily, or employing sophisticated ensemble methods that integrate multiple models to better handle the class distribution skew. Effective strategies strive to improve the representation and prediction accuracy of tail classes without compromising the overall model performance. The field is actively evolving, seeking robust and adaptable solutions that handle real-world distribution shifts and accommodate varying user preferences, making long-tail learning a critical area of research within machine learning.

Hypernetwork Experts

#

The concept of “Hypernetwork Experts” presents a novel approach to long-tailed learning. A hypernetwork acts as a central generator, creating diverse expert models tailored to various data distributions and user preferences. This contrasts with traditional single-model or fixed multi-expert approaches. The hypernetwork’s flexibility is key, allowing for the dynamic generation of models optimized for specific needs, such as prioritizing tail class accuracy or balancing performance across all classes. This adaptability makes the approach especially robust to distribution shifts often encountered in real-world scenarios. The diverse expert models created by the hypernetwork likely cover a wider range of data characteristics, leading to better generalization and performance ceilings. However, challenges exist; efficient training of both the hypernetwork and the generated experts needs attention, and managing the computational cost associated with multiple models should be considered. Control over the generated experts’ behaviors is a significant advantage, facilitating adjustable trade-offs between competing objectives depending on the application’s needs. The interpretability of the method, linked to the controllable generation of specialized models, makes it promising.

Preference Control

#

The concept of ‘Preference Control’ in a long-tailed learning context is groundbreaking. It moves beyond simply optimizing overall accuracy, acknowledging that real-world applications often prioritize different aspects depending on the specific task and user needs. The ability to flexibly adjust the model’s focus on head versus tail classes is crucial, especially when dealing with imbalanced data. This approach introduces a new level of interpretability and control, enabling users to specify their preferred trade-offs between recall and precision for head and tail classes. The preference vector, used to guide the model’s behavior during inference, allows for a dynamic and adaptive model, responsive to the changing demands of different scenarios. The described method’s capability to control the head-tail trade-off offers considerable practical advantages, particularly in domains with safety and cost implications. This represents a significant advancement in making long-tailed learning methods more versatile and user-friendly.

Distribution Shift

#

The concept of ‘Distribution Shift’ in machine learning, particularly within the context of long-tailed learning, is crucial. It highlights the discrepancy between training and testing data distributions, impacting model generalization. Methods that assume similar distributions during training and testing often fail when applied to real-world scenarios where distribution shifts are common. This necessitates more robust approaches that can adapt to diverse and unseen data distributions, a key challenge in applying long-tailed learning to practical problems. The research emphasizes the importance of creating models that are not only high-performing but also robust to various distribution shifts encountered in real-world datasets, which are often imbalanced. Addressing distribution shift is paramount for building reliable and effective long-tailed learning models that generalize well beyond the confines of their training data. A controllable paradigm that dynamically adjusts to user preferences, and differing degrees of imbalance, is shown to be highly desirable. This ensures the produced model not only adapts to data distribution shifts but also prioritizes different classes according to the specific requirements of the application.

Future of PRL

#

The future of PRL (Preference-controlled Robust Long-tailed learning) is promising, building upon its success in addressing long-tailed learning challenges and distribution shifts. Further research could focus on enhancing the hypernetwork’s efficiency and scalability, perhaps through novel architectures or training techniques. Investigating the application of PRL to other challenging machine learning domains, like few-shot learning or domain adaptation, is also warranted. Exploring different preference elicitation methods could improve usability and interpretability. Finally, rigorous empirical evaluations on diverse, real-world datasets are needed to solidify its robustness and establish benchmarks for future comparison. Future work could also incorporate uncertainty quantification and explainability aspects, boosting trustworthiness and practical adoption.

More visual insights

#

More on figures

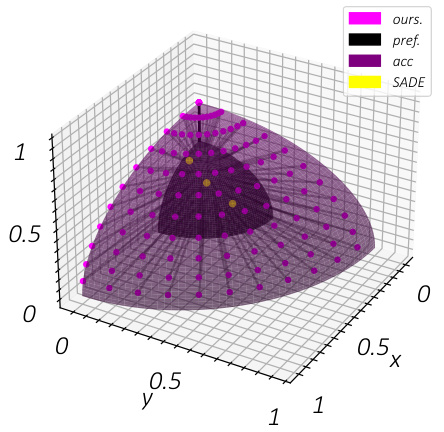
This figure visualizes the relationship between user preferences and model performance. The three-dimensional coordinate system represents the performance on the forward50, uniform, and backward50 splits of the CIFAR100-LT dataset. The dark plane represents the performance on the three distributions for different preference vectors. Yellow dots represent the results of running SADE, while purple dots show our method’s results. The figure shows that our method covers various distributions with a single training and outperforms SADE by satisfying different user preferences.

This figure compares three different approaches to long-tailed learning. (a) shows the traditional approach, where a single model is trained on a specific long-tailed distribution. (b) shows a multi-expert approach, where multiple experts are trained on different distributions. This approach is limited as the distribution of the data is pre-defined and cannot be changed. (c) shows the proposed method, which uses hypernetworks to generate diverse expert models that can adapt to any test distribution. The method allows for flexible adjustment of the head-tail trade-off according to user preferences. This approach is more flexible and robust, as it can handle various distribution scenarios and satisfy the user’s requirements for performance on head and tail classes.

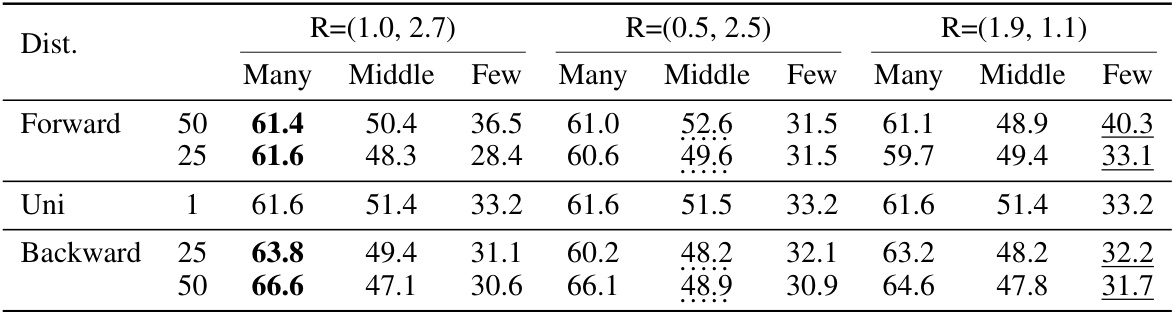
This figure visualizes the relationship between user preferences and model performance. The three-dimensional coordinate system represents the performance on forward50, uniform, and backward50 splits of the CIFAR100-LT dataset. The dark plane shows the performance with no preference input. The red points indicate preference vectors that improve performance on the many-shot classes. The green points represent preference vectors that hurt performance on the many-shot classes. The figure demonstrates the flexibility of the proposed method in controlling performance trade-offs based on user preferences.

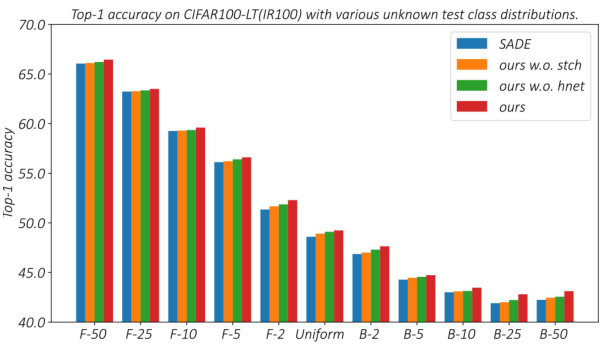
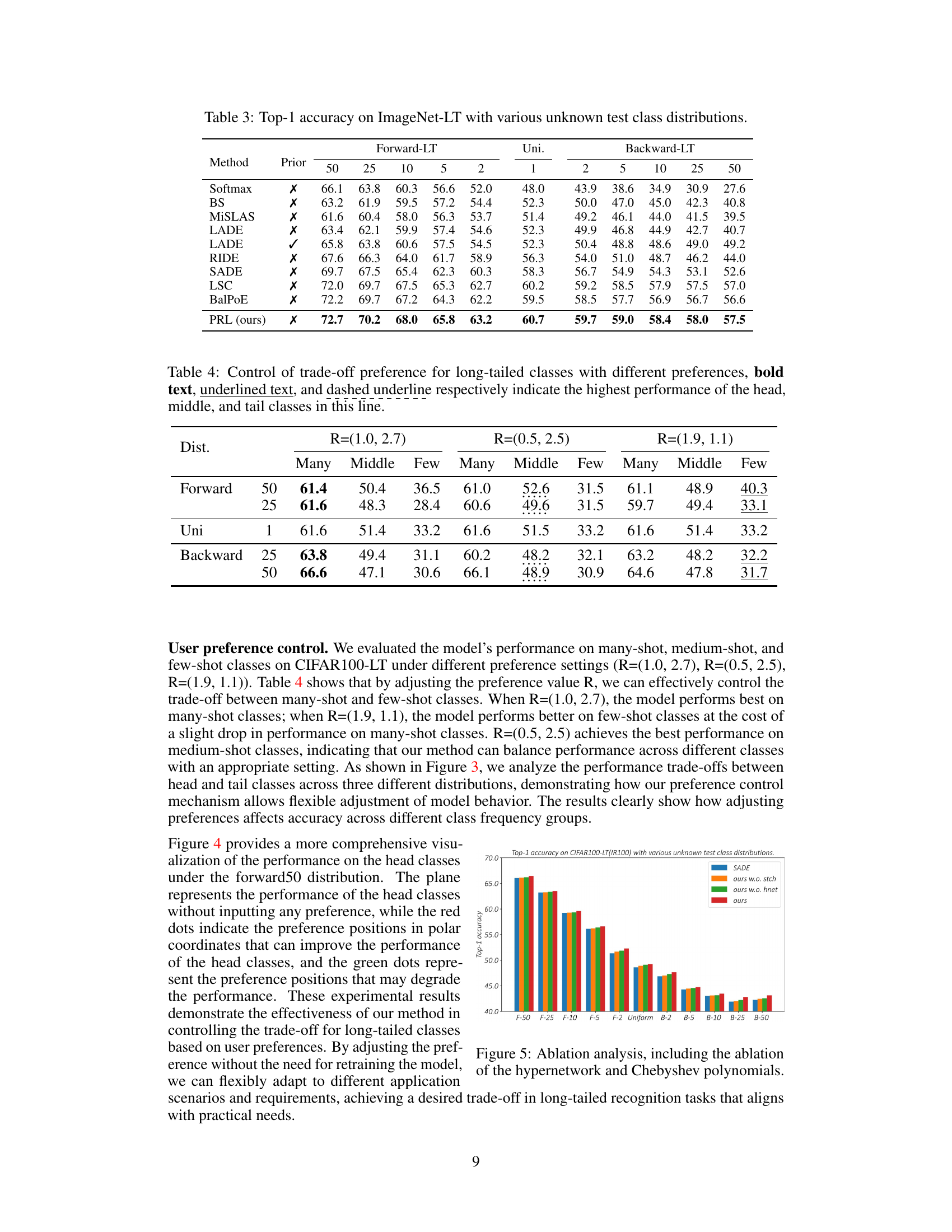
This figure presents the results of ablation studies conducted on the CIFAR100-LT dataset (IR100) to evaluate the impact of removing the hypernetwork (w.o. hnet) and the Chebyshev polynomial (w.o. stch) on model performance under various unknown test class distributions. The x-axis shows different test distributions, ranging from those heavily biased toward many-shot classes (F-50) to those biased toward few-shot classes (B-50), with a uniform distribution in the middle. The y-axis represents the Top-1 accuracy achieved. The four colored bars for each distribution show the performance of the full model (‘ours’), the model without the stochastic convex ensemble (‘ours w.o. stch’), the model without the hypernetwork (‘ours w.o. hnet’), and the SADE baseline.

More on tables

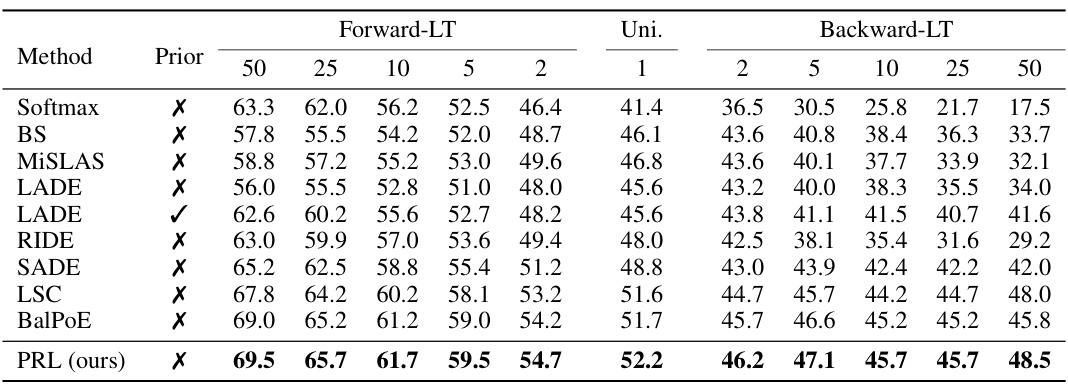
This table presents the top-1 accuracy results on the CIFAR100-LT dataset (imbalance ratio of 100) under various unknown test class distributions. The distributions tested are: Forward-LT (head classes over-represented), Uniform (balanced), and Backward-LT (tail classes over-represented). The results are shown for different proportions of each class in the test set, allowing analysis of the model’s performance across various distribution shifts. The ‘Prior’ column indicates whether the prior probabilities of the test data were used during testing. This allows for evaluating the method’s adaptability to various real-world distribution shifts and understanding its performance relative to different test conditions.

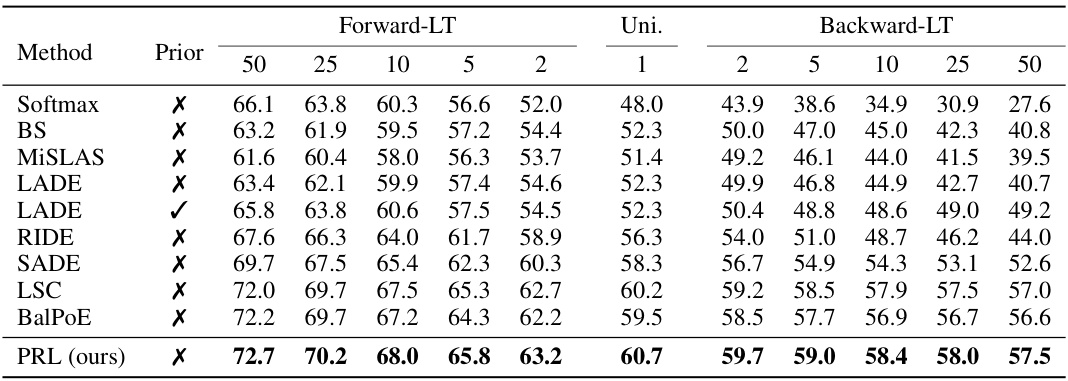
This table presents the top-1 accuracy results on the CIFAR100-LT dataset (imbalance ratio of 100) using various test set distributions. The different distributions represent varying degrees of head-tail class imbalance, ranging from forward-biased (forward-LT), uniform (Uni.), to backward-biased (backward-LT) distributions. The results allow a comparison of different models’ performance across different test set distribution scenarios.

This table presents the Top-1 accuracy results on the CIFAR100-LT dataset (imbalance ratio of 100) under various unknown test class distributions. It compares the performance of several long-tailed recognition methods including Softmax, Balanced Softmax, MiSLAS, LADE (with and without prior knowledge), RIDE, SADE, LSC, BalPoE, and the proposed PRL method. The distributions considered are forward-LT (where tail classes are more frequent in testing), uniform (equal distribution), and backward-LT (where head classes are more frequent in testing). The results show how each model performs across various scenarios of class distribution in test data.

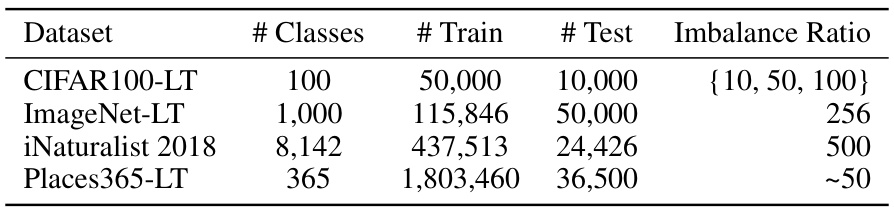
This table presents the key statistics for four long-tailed image datasets used in the paper’s experiments: CIFAR100-LT, ImageNet-LT, iNaturalist 2018, and Places365-LT. For each dataset, it lists the number of classes, the number of training images, the number of test images, and the imbalance ratio (the ratio between the most frequent class and least frequent class). The imbalance ratios vary significantly across datasets, reflecting the varying degrees of class imbalance common in real-world scenarios.

This table presents the top-1 accuracy results of several state-of-the-art long-tailed recognition methods and the proposed PRL method on four benchmark datasets: CIFAR100-LT, Places-LT, iNaturalist 2018, and ImageNet-LT. The test class distribution is uniform across all datasets, providing a comparison under standard long-tailed recognition settings. The results showcase the performance of different approaches in handling class imbalances in the context of balanced testing data.

This table presents the top-1 accuracy results achieved by various state-of-the-art long-tailed recognition methods and the proposed PRL method on four benchmark datasets: CIFAR100-LT, Places-LT, iNaturalist 2018, and ImageNet-LT. The key characteristic is that the test data distribution is uniform, allowing for a direct comparison of model performance under standard evaluation conditions. The results showcase the superior performance of PRL compared to other methods across all datasets.

This table presents the top-1 accuracy results on CIFAR100-LT with an imbalance ratio (IR) of 100, across various unknown test class distributions, comparing several long-tailed learning methods. The distributions include forward-LT (skewed towards head classes), uniform, and backward-LT (skewed towards tail classes). The ‘Prior’ column indicates whether prior information was used in the method. The table provides a detailed comparison of performance across different scenarios, illustrating the relative strengths and weaknesses of each approach when dealing with distribution shifts and class imbalance.

This table presents the Top-1 accuracy results on the CIFAR100-LT dataset (imbalance ratio of 100) under various unknown test class distributions. It compares different methods’ performance across different test set distributions: forward-LT (skewed towards head classes), uniform (balanced), and backward-LT (skewed towards tail classes). The results are further broken down by the number of samples per class (Prior) in the test distribution. This allows for an in-depth analysis of each method’s robustness to varying distribution shifts and the impact of class imbalance.

This table shows the model size (in MB) and computational cost (in GFLOPs) for different models (ResNet-32, ResNeXt-50, ResNet-50) with and without the hypernetwork. The hypernetwork increases the number of parameters but doesn’t significantly impact the computational cost.

Full paper

#