Stabilized Proximal-Point Methods for Federated Optimization

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in federated learning due to its significant advancements in communication and computation efficiency. It introduces novel algorithms that are provably efficient and adaptable, opening new avenues for research and development in this rapidly growing field. The work’s focus on adaptive algorithms is particularly relevant to the practical challenges of federated learning.

Visual Insights

#

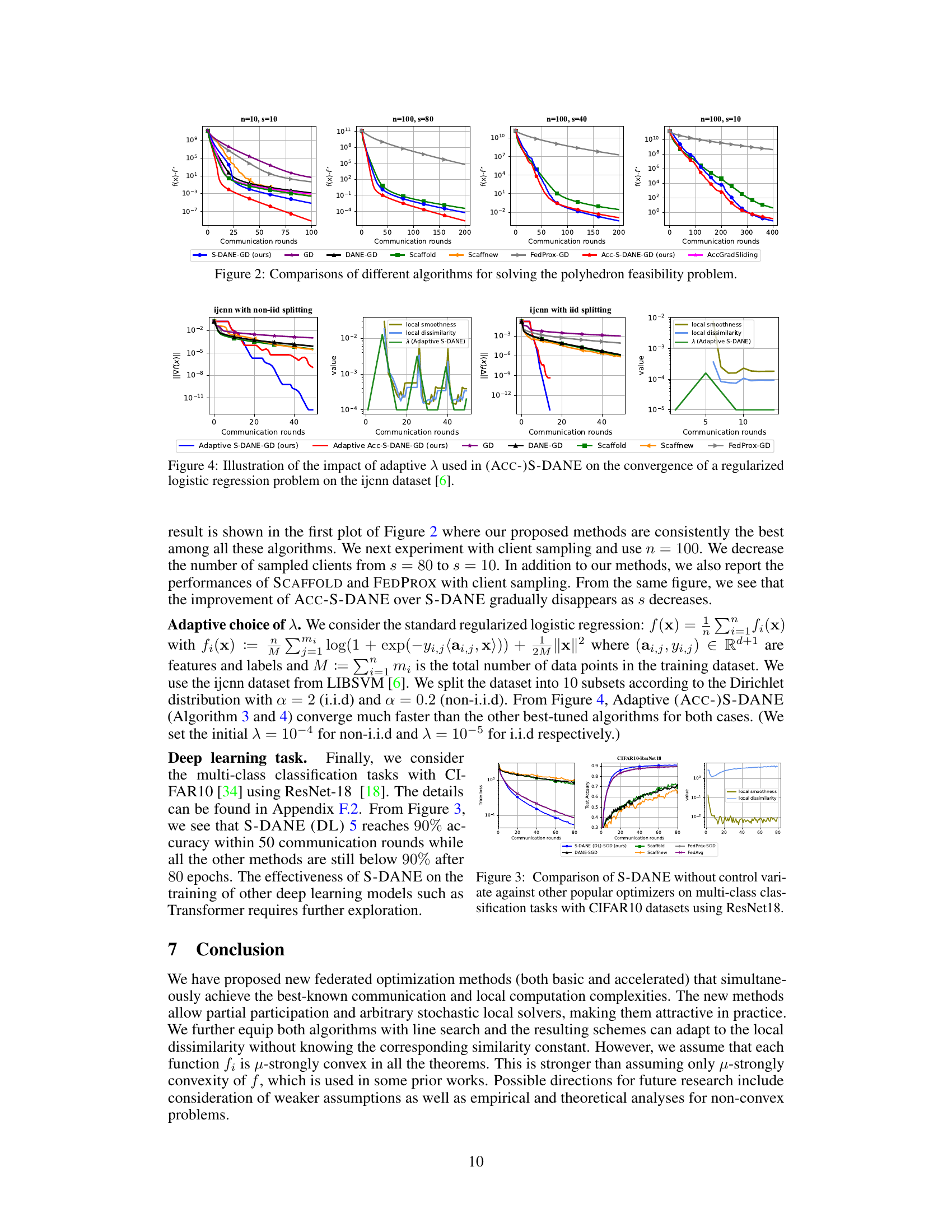
This figure compares three algorithms (S-DANE, ACC-S-DANE, and DANE) on a convex quadratic minimization problem using gradient descent as the local solver. It highlights the improved local computation efficiency of S-DANE over DANE and the further communication complexity improvement of ACC-S-DANE. The adaptive variants of the algorithms are also shown to leverage local dissimilarities for enhanced performance.

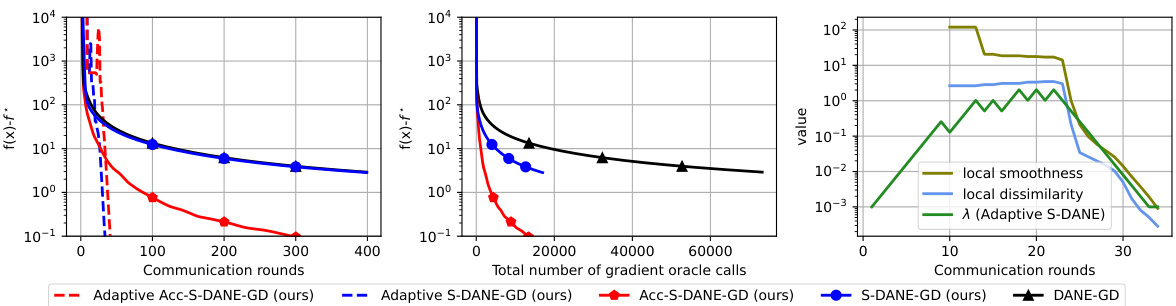
This table summarizes the convergence rates of various distributed optimization algorithms. It compares their communication complexity (number of communication rounds and vectors communicated per round) and local computation complexity (number of local gradient queries). The algorithms are categorized by whether they handle general convex or strongly convex functions and whether their convergence guarantee is deterministic or in expectation. The table also defines key parameters like L-smoothness, µ-convexity, and second-order dissimilarity (δ).

In-depth insights

#

Stabilized Prox-Point

#

The concept of “Stabilized Prox-Point” methods, as discussed in the context of the research paper, centers on addressing the limitations of traditional proximal-point methods in optimization problems, especially within the context of federated learning. Standard proximal-point methods often require high accuracy in solving local subproblems at each iteration, leading to suboptimal local computational efficiency. The “stabilized” approach introduces an auxiliary sequence of prox-centers, effectively improving the accuracy condition for solving these subproblems. This milder accuracy requirement translates to enhanced local computation efficiency without compromising the deterministic communication complexity. The stabilization technique is particularly valuable in distributed settings where communication is costly, as it allows for faster convergence with reduced communication rounds. The key innovation lies in the improved balance between local computation and communication costs, making the approach more practical for large-scale federated learning applications. The introduction of adaptive variants further enhances its applicability by removing the need for prior knowledge of key parameters.

S-DANE Algorithm

#

The S-DANE algorithm, a stabilized distributed proximal-point method, presents a significant advancement in federated optimization. It addresses the communication bottleneck inherent in federated learning by improving upon the DANE algorithm. S-DANE cleverly introduces an auxiliary sequence of prox-centers, enhancing local computation efficiency while maintaining the same deterministic communication complexity as DANE. This is achieved through a milder accuracy condition for solving the local subproblems, making it more practical. The algorithm’s flexibility is further amplified by its support for partial client participation and arbitrary stochastic local solvers, adapting well to the realities of distributed environments. Moreover, accelerated versions of S-DANE, like ACC-S-DANE, offer further improvements, achieving the best-known communication complexity among existing methods. These improvements are particularly notable given the algorithm’s continued focus on practical efficiency, making it a powerful tool for a wide range of applications.

Adaptive Variants

#

The concept of ‘Adaptive Variants’ in the context of optimization algorithms, specifically within the domain of federated learning, is crucial for practical applicability. Adaptive algorithms automatically adjust parameters based on the data characteristics, eliminating the need for prior knowledge of crucial constants (like the similarity constant in this paper’s setting). This is a significant advantage because such constants are often unknown and can vary drastically across datasets and federated learning scenarios. The line search technique employed allows for this dynamic adaptation, ensuring convergence efficiency even under heterogeneous data distributions. The inclusion of adaptive versions of both the core algorithm and its accelerated counterpart highlights a commitment to robustness and practical usability. While the theoretical guarantees might be slightly weaker for the adaptive versions compared to their non-adaptive counterparts (often involving an additional logarithmic factor), this trade-off is often justified by the improvement in real-world performance. The adaptive variants represent a key step towards bridging the gap between theoretical guarantees and practical deployment of sophisticated federated learning optimization algorithms.

Communication Speedup

#

The concept of “Communication Speedup” in distributed optimization, particularly within federated learning, centers on minimizing the communication overhead between clients and the central server. Efficient algorithms leverage techniques like reduced data transmission, exploiting local computation, and utilizing second-order information. The paper likely explores how similarities in local datasets or model structures can reduce the amount of data exchanged. This similarity allows for the use of compressed communication or the transmission of only essential differences, leading to significant speed gains. The effectiveness of these approaches depends on the degree of similarity among clients; higher similarity translates to greater speedup potential. However, achieving high accuracy in local subproblem solving might offset some communication savings, as this step can become computationally demanding. Therefore, finding the right balance between communication efficiency and local computation cost remains crucial for practical implementation. Adaptive algorithms that dynamically adjust parameters based on observed local properties are especially attractive as they adapt to varying levels of data similarity without prior knowledge. The paper likely presents quantitative results demonstrating the communication speedup achieved by proposed methods, highlighting their efficiency compared to standard benchmarks.

Future Research

#

Future research directions stemming from this work on stabilized proximal-point methods for federated optimization could explore relaxing the strong convexity assumption on individual functions, a limitation of the current theoretical analysis. Investigating the performance and theoretical guarantees for non-convex problems would be highly valuable. Furthermore, a deeper examination into the impact of different local solvers on the overall convergence and efficiency, extending beyond the simple gradient descent used in some experiments, is warranted. Finally, developing more sophisticated and potentially adaptive strategies for client sampling and handling unreliable or heterogeneous clients would enhance the practicality and robustness of these methods in real-world federated learning scenarios.

More visual insights

#

More on figures

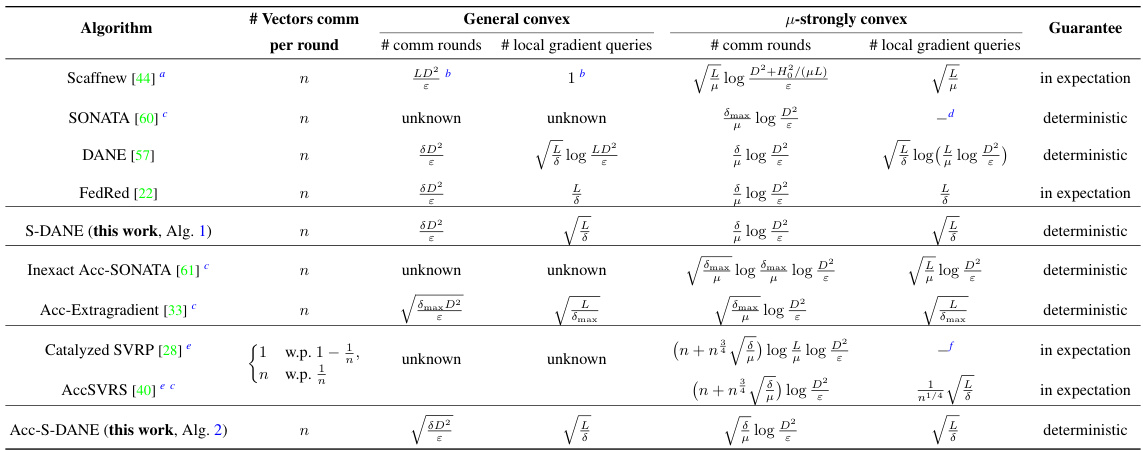
This figure compares several algorithms for solving a strongly convex polyhedron feasibility problem, including S-DANE, ACC-S-DANE, GD, DANE-GD, Scaffold, FedProx-GD, and AccGradSliding. Different settings are shown, varying the number of total clients (n) and the number of clients sampled per round (s). The vertical axis represents the objective function value (f(x) - f*), while the horizontal axis represents the number of communication rounds. The figure demonstrates the superior performance of S-DANE and ACC-S-DANE, particularly in settings with limited client participation (smaller s values).

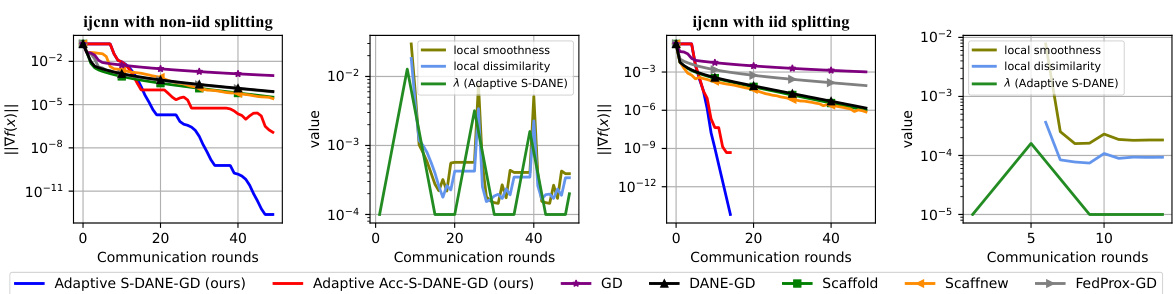
The figure compares the performance of three algorithms (S-DANE, ACC-S-DANE, and DANE) in solving a convex quadratic minimization problem. All use gradient descent as the local solver. The plots illustrate the convergence speed in terms of communication rounds and the number of local gradient calls. S-DANE shows improved local efficiency over DANE, while ACC-S-DANE further improves communication complexity. The adaptive versions of the algorithms demonstrate the advantage of leveraging local dissimilarities for better performance.

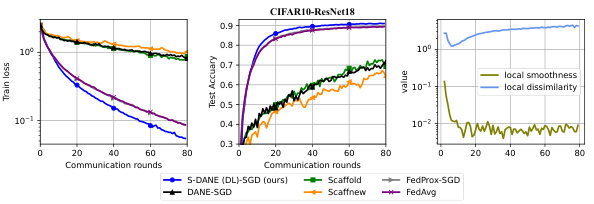
This figure compares the performance of three algorithms (S-DANE, ACC-S-DANE, and DANE) on a convex quadratic minimization problem. All use gradient descent (GD) as the local solver. The results show that S-DANE improves local computation efficiency over DANE, and ACC-S-DANE further enhances communication complexity. The adaptive versions of the algorithms demonstrate the ability to use local dissimilarity for better performance.

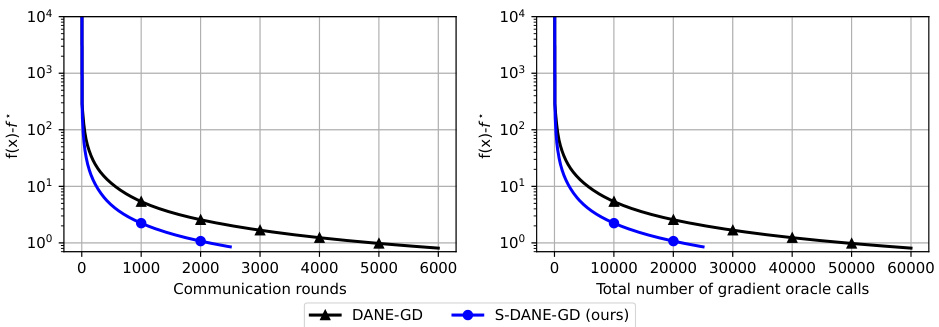
This figure compares the performance of three algorithms (DANE, S-DANE, and ACC-S-DANE) on a convex quadratic minimization problem. All algorithms use gradient descent as the local solver. The plots show that S-DANE achieves the same communication complexity as DANE but with improved local computation efficiency. ACC-S-DANE improves upon both communication complexity and local computation efficiency. Furthermore, adaptive versions of these algorithms demonstrate even better performance by leveraging local dissimilarities.

Full paper

#