Non-asymptotic Approximation Error Bounds of Parameterized Quantum Circuits

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in quantum machine learning because it provides a theoretical foundation for designing practical parameterized quantum circuits (PQCs) and quantum neural networks, paving the way for more efficient and scalable quantum machine learning algorithms. It also offers a direct comparison of PQCs with classical neural networks, providing valuable insights for the field.

Visual Insights

#

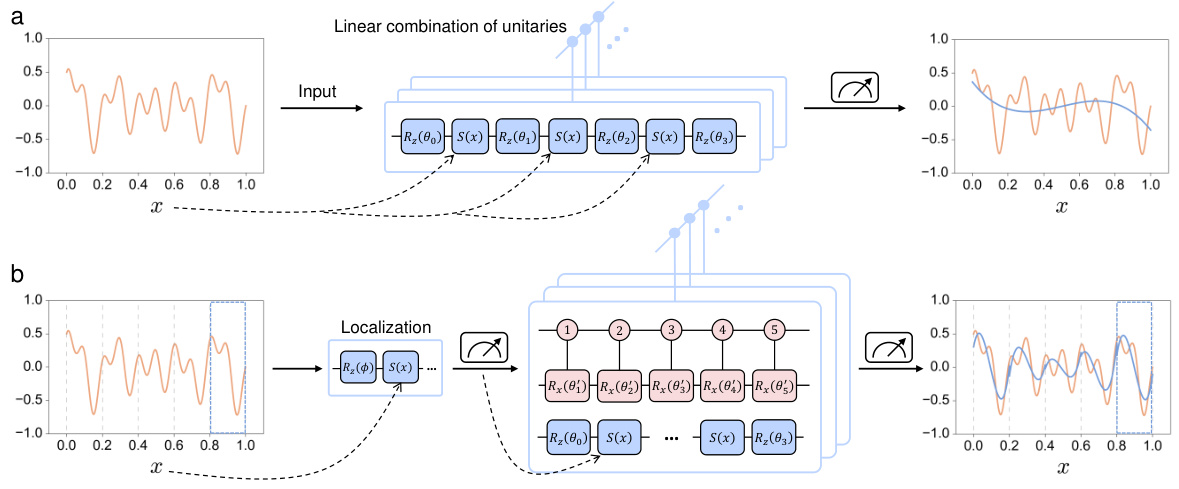
This figure shows two different approaches for approximating continuous functions using parameterized quantum circuits (PQCs). (a) uses Bernstein polynomials, encoding the input and applying a series of gates to produce a polynomial approximation. (b) uses local Taylor expansions, first localizing the input to a smaller region and then applying a Taylor expansion in that region. Both methods involve fine-tuning parameters within the PQCs to optimize the approximation.

This table compares the approximation errors of Parameterized Quantum Circuits (PQCs) and Rectified Linear Unit feedforward neural networks (ReLU FNNs) for approximating multivariate monomials and smooth functions in C([0,1]d). It shows the width, depth, number of parameters, and approximation error for each approach, highlighting the differences in resource requirements and approximation capabilities. The approximation error for PQCs is 0 for multivariate monomials because they can be implemented exactly using the described constructions. For smooth functions in C([0,1]d), both the nested PQCs and ReLU FNNs achieve an approximation error that decreases with increasing K (number of partitions) and N (width of the FNN), respectively, though the scaling behavior is different for the two models.

In-depth insights

#

Quantum Expressivity

#

Quantum expressivity, a central theme in quantum machine learning, explores the power of quantum circuits to represent and approximate complex functions. This contrasts with classical machine learning models. The key question is whether quantum systems offer an advantage in representing high-dimensional functions. Research into quantum expressivity often involves deriving bounds on approximation errors, showing how well a quantum circuit can approximate a target function given its size and depth. A significant challenge lies in demonstrating that the improvement comes from quantum mechanics and not from clever classical data processing. This is typically addressed by explicitly constructing quantum circuits without relying on classical pre- or post-processing steps. Data encoding schemes and the choice of measurements play crucial roles, affecting a quantum circuit’s ability to approximate specific function classes. Theoretical results often establish the conditions under which quantum circuits achieve universal approximation, meaning they can approximate any function with sufficient resources. Practical applications hinge on the efficiency of quantum circuits, making it essential to compare their sizes and parameter counts against classical counterparts to gauge any quantum advantage. Numerical experiments play a critical role in validating theoretical findings and exploring the practical implementation challenges.

PQC Approximation

#

The study delves into parameterized quantum circuits (PQCs) and their capability of approximating various function classes. A core focus is establishing non-asymptotic approximation error bounds, moving beyond previous universal approximation theorems that lack explicit construction or rely on classical data processing. The research presents explicit PQC constructions for approximating multivariate polynomials and smooth functions, achieving parameter efficiency comparable to classical neural networks. Novel error bounds are derived in terms of circuit size and trainable parameters, demonstrating potential advantages over classical deep neural networks in certain scenarios. Numerical experiments validate the theoretical findings, showcasing successful approximation of multivariate functions. The work provides a theoretical foundation for designing practical PQCs and quantum neural networks and contributes to the advancement of quantum machine learning.

Numerical Analysis

#

A robust numerical analysis section in a research paper on parameterized quantum circuits (PQCs) would involve more than simply presenting results; it would delve into the methodology’s effectiveness and limitations. Detailed descriptions of the experimental setup are crucial, including the specific quantum computing platform, the choice of optimizers (e.g., Adam), learning rates, and the number of training epochs. A comparison of PQC performance against classical counterparts (like deep ReLU neural networks) on benchmark datasets, using established metrics like mean squared error (MSE), would provide strong validation. Furthermore, a discussion of the generalizability and scalability of the PQCs is vital, exploring factors affecting approximation accuracy, such as circuit depth and the number of trainable parameters. Finally, error analysis, including the assessment of statistical significance (e.g., through error bars or confidence intervals), would solidify the claims made regarding the PQCs’ approximation capabilities. In short, a strong numerical analysis section should offer clear, reproducible experiments and a nuanced evaluation of the methodology’s strengths and weaknesses.

Approximation Bounds

#

The concept of ‘Approximation Bounds’ in a machine learning context, particularly within the realm of quantum machine learning, is crucial for understanding the capabilities and limitations of a model. Tight approximation bounds demonstrate that a model can effectively approximate target functions with specific error guarantees. This is especially valuable for quantum models, where the physical implementation has resource constraints such as the number of qubits and the depth of the circuit. Non-asymptotic bounds, which provide error guarantees for finite resources, are particularly important for near-term quantum devices. The paper likely explores these bounds in relation to parameterized quantum circuits (PQCs), comparing their approximation capabilities to classical models like deep neural networks. A key aspect of this analysis would be the dependence of error bounds on the number of parameters, circuit depth, and possibly function characteristics like smoothness. The analysis will reveal whether PQCs offer any advantage in terms of approximation efficiency, highlighting the potential for quantum speed-up in machine learning.

Future Research

#

The paper’s conclusion suggests several promising avenues for future research. Developing more efficient training strategies for PQCs is crucial, potentially exploring accelerated methods to achieve faster convergence rates. The current work focuses on approximating specific function classes; extending this to more complex, real-world datasets and tasks is vital. Investigating the approximation capabilities of PQCs with different quantum gates and architectures could unlock further performance improvements. A direct comparison with other quantum machine learning models would help establish the relative strengths of PQCs. Finally, exploring the potential of PQCs in more practical machine learning tasks, like image recognition or natural language processing, is vital to demonstrate their real-world applicability and uncover potential quantum advantages.

More visual insights

#

More on figures

This figure illustrates two different strategies for approximating continuous functions using parameterized quantum circuits (PQCs). The first uses Bernstein polynomials, encoding the input into the PQC and using a linear combination of unitaries to aggregate polynomials. The second uses local Taylor expansions, first localizing the input into regions and then using PQCs to implement local Taylor expansions in each region.

This figure shows the results of using single-qubit parameterized quantum circuits (PQCs) to approximate a piecewise constant localization function D(x). Two different scenarios are presented: one with K=2 intervals and another with K=10 intervals. The plots illustrate the PQC output versus the input x, demonstrating the approximation capability of the PQCs. The approximation improves as the number of intervals (K) increases.

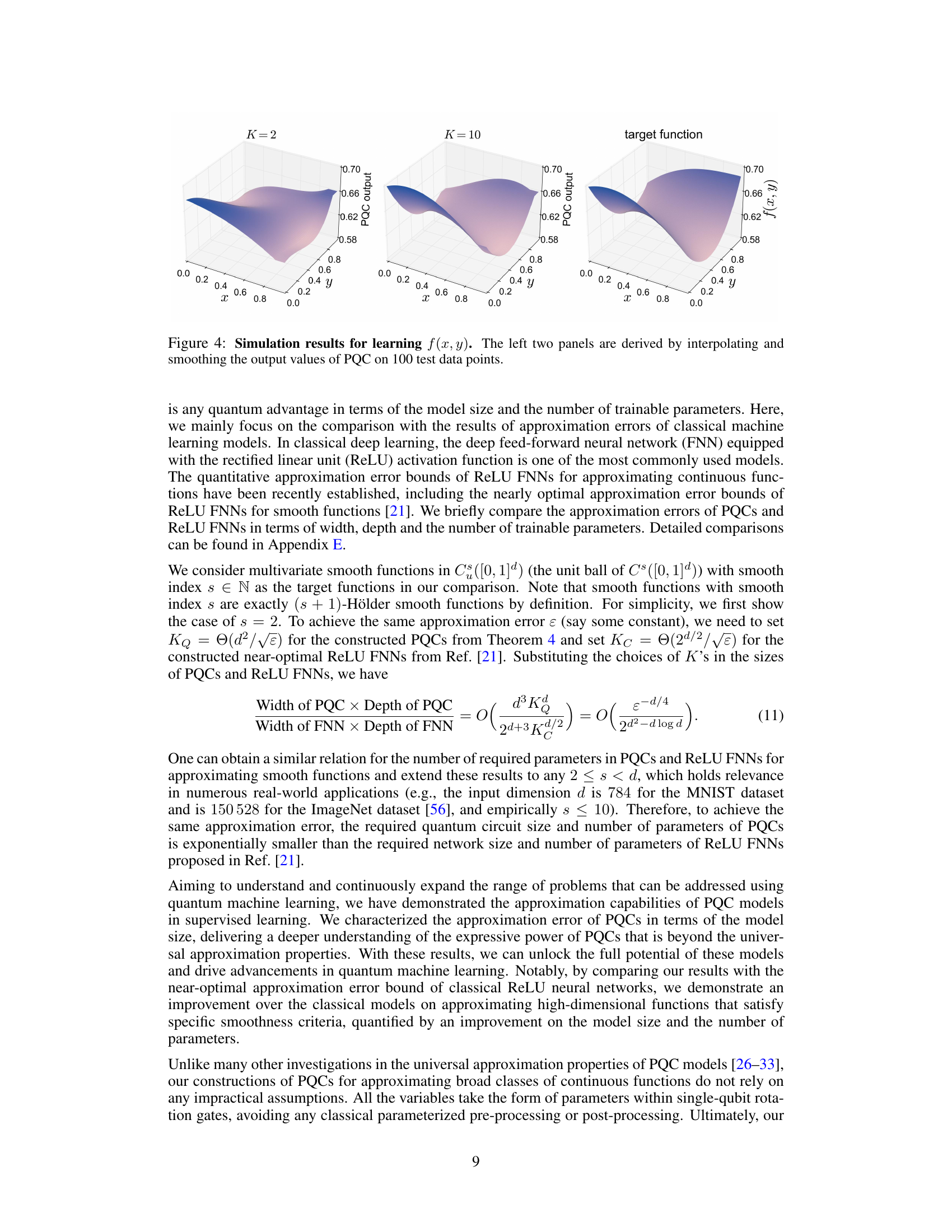
This figure shows the results of numerical experiments for approximating a bivariate polynomial function using PQCs. The left two panels display the PQC’s output for K=2 and K=10, respectively, while the right panel shows the target function. The approximation process involves two steps: 1) learning a piecewise-constant function; and 2) learning the Taylor expansion of the target function. The results demonstrate improved approximation performance as K increases, aligning with theoretical findings. The K value represents the number of intervals for the piecewise-constant function.

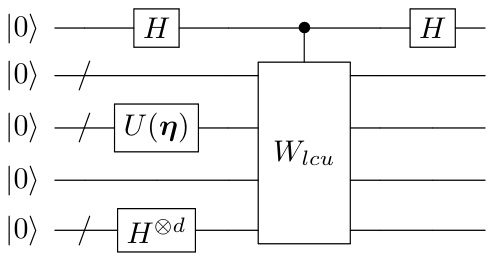
This figure shows two different approaches for approximating continuous functions using parameterized quantum circuits (PQCs). (a) uses Bernstein polynomials, encoding the input and combining multiple polynomials. (b) uses local Taylor expansions, localizing the input and combining Taylor expansions for better approximation. Both methods involve fine-tuning trainable parameters in quantum gates.

Full paper

#