↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Deep learning models trained on sensitive data raise significant privacy concerns. Membership Inference Attacks (MIAs) are commonly used to evaluate model privacy by determining if specific data points were used in training. Current MIAs often rely on model outputs like prediction probabilities or loss values. However, these methods can be unreliable or ineffective, particularly with large datasets or models with strong privacy mechanisms. This necessitates a robust and more accurate method for assessing model privacy.
This research introduces a novel approach to MIA leveraging input loss curvature, which is the trace of the Hessian of the loss function with respect to the input data. The authors develop a theoretical framework that establishes an upper bound on the distinguishability of train and test data based on input loss curvature, dataset size, and differential privacy parameters. They propose a new black-box MIA using zero-order input loss curvature estimation which is more effective than current state-of-the-art methods. Experiments on various datasets (CIFAR10, CIFAR100, ImageNet) confirm the superiority of the curvature-based MIA, especially for larger datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and privacy because it bridges the gap between theoretical understanding and practical application of input loss curvature. It provides a novel membership inference attack method and a theoretical framework, which are valuable tools for evaluating the privacy of machine learning models and developing new privacy-preserving techniques. The insights gained from this research are highly relevant to the current trends of improving the privacy and security of machine learning systems.
Visual Insights#

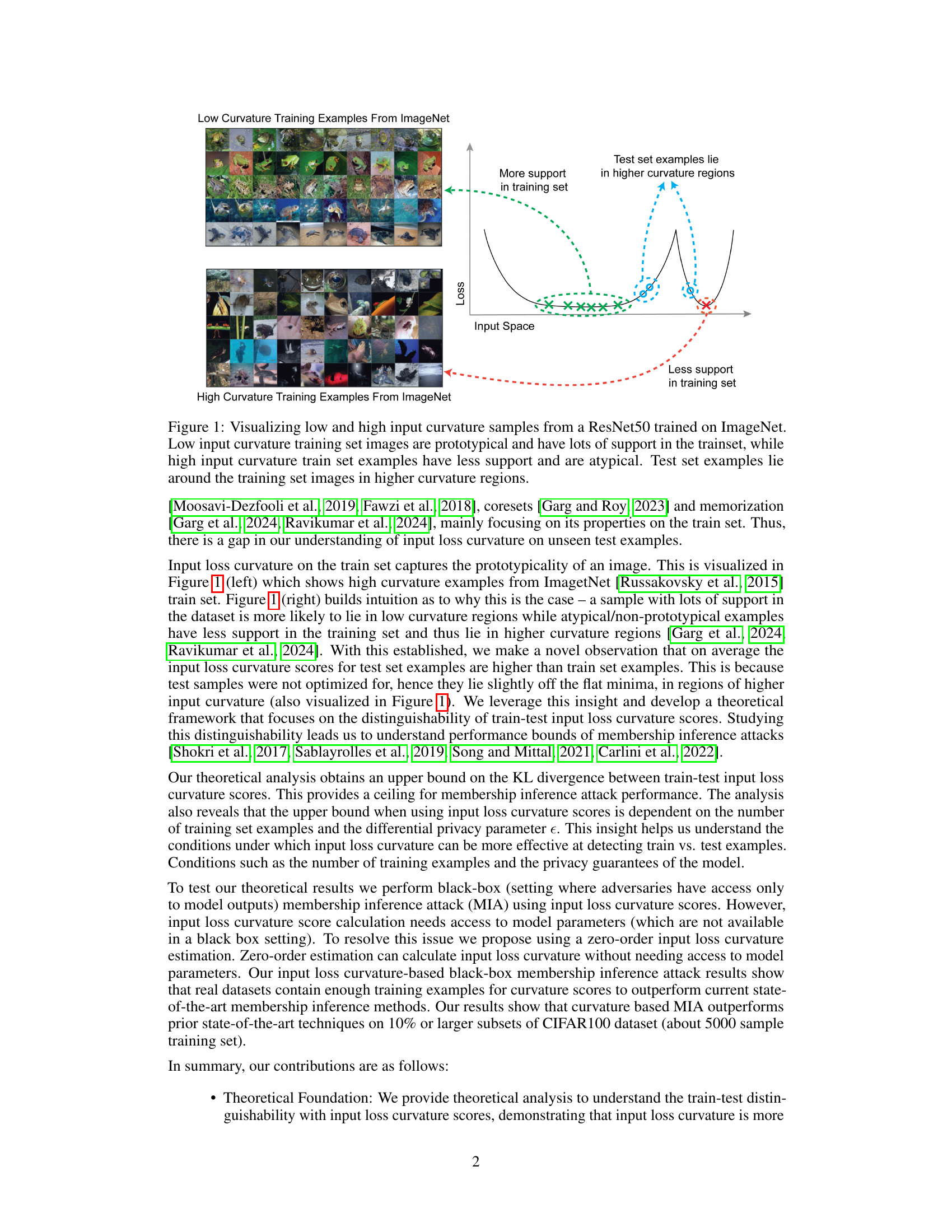
This figure visualizes the concept of input loss curvature in the context of ImageNet. It shows that low-curvature training examples are prototypical images with lots of similar images in the training set, while high-curvature training examples are less common or atypical, thus the model is less confident and memorizes them. Test examples tend to fall in higher-curvature regions which is slightly off from the flat minima, representing less confident prediction and memorization.
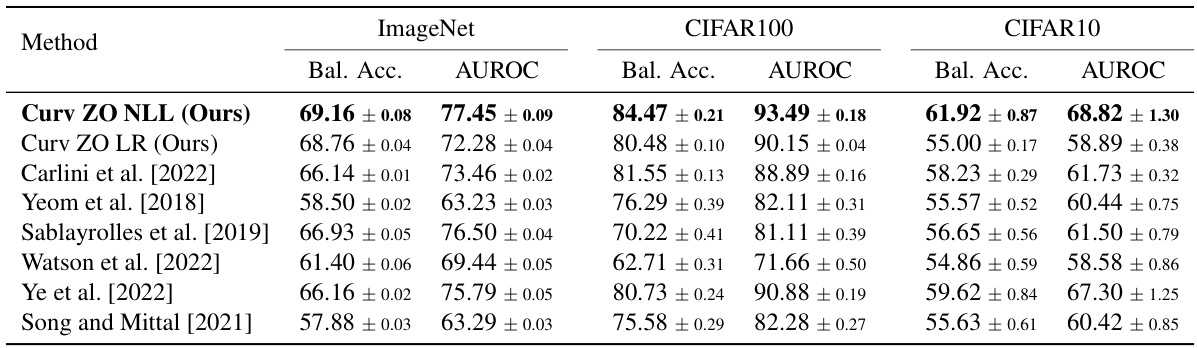
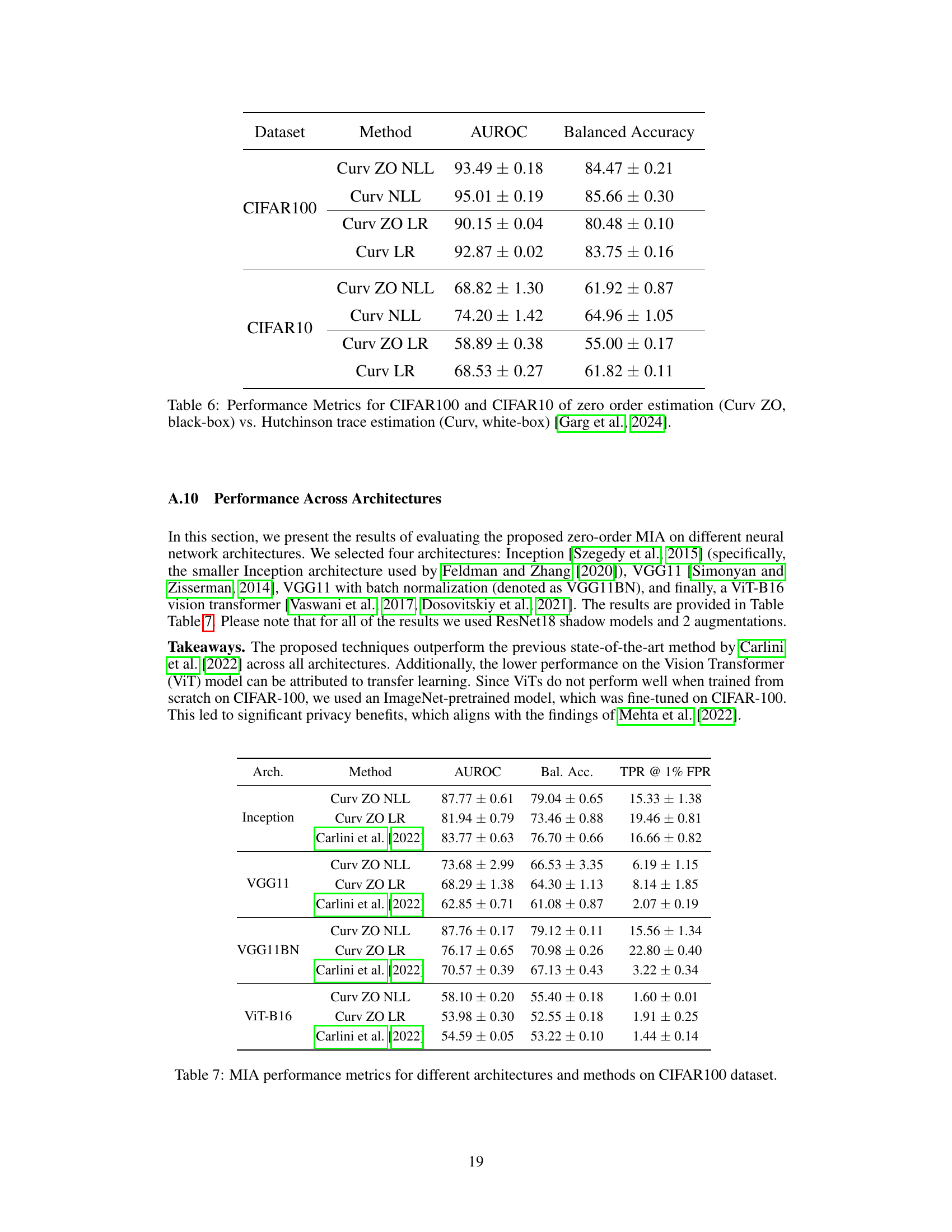
This table compares the performance of the proposed curvature-based membership inference attack (MIA) with several existing MIA methods. The comparison is done across three different datasets: ImageNet, CIFAR100, and CIFAR10. The metrics used for comparison are balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve). The results presented are the average values and standard deviations obtained from three independent runs.
In-depth insights#
Loss Curvature Clues#
The concept of “Loss Curvature Clues” in deep learning privacy research is intriguing. It suggests that the curvature of the loss function with respect to the input data can reveal sensitive information about the training data, acting as a hidden signal or “clue.” High curvature regions may indicate data points that are atypical or less representative of the training distribution, potentially exposing privacy vulnerabilities. Conversely, low curvature regions might reflect prototypical data points memorized by the model, again raising privacy concerns. Analyzing loss curvature could lead to improved membership inference attacks (MIAs), which aim to determine if a specific data point was part of a model’s training set. Furthermore, understanding these clues can potentially inform the development of stronger privacy-preserving techniques, enabling the creation of models that are less susceptible to such attacks by either mitigating high-curvature regions or by ensuring that the model does not memorize overly specific features of the training data.
MIA Attack Enhancements#
Membership Inference Attacks (MIAs) aim to determine if a specific data point was used in a model’s training. Enhancements to MIA attacks often focus on improving their accuracy and efficiency. This might involve developing new techniques to better estimate the likelihood of membership, such as using input loss curvature or other more nuanced metrics beyond simple loss or confidence scores. Advanced MIAs could incorporate adversarial examples or data augmentation strategies to make the attack more robust and less susceptible to defensive mechanisms. There is a strong emphasis on adapting MIAs to work in black-box settings, where the attacker only has access to model outputs, rather than internal parameters. Research also explores the theoretical underpinnings of MIA success, aiming to derive tighter bounds on attack performance based on factors such as training dataset size and the model’s differential privacy guarantees. Ultimately, the goal of MIA enhancement is to develop more potent tools for evaluating and improving the privacy of machine learning models while advancing the understanding of deep learning vulnerabilities.
Zero-Order Estimation#
Zero-order estimation methods are crucial when dealing with black-box scenarios, where internal model parameters are inaccessible. In the context of this research paper, it is specifically vital for estimating input loss curvature, a key metric for membership inference attacks. The brilliance of using zero-order methods lies in its ability to approximate the curvature using only input and output information, bypassing the need for internal model gradients. This is achieved through clever numerical techniques, such as finite-difference approximations, which replace the computation of gradients with carefully designed function evaluations around the input point. While computationally more expensive than gradient-based methods, this approach proves invaluable for situations where gradient access is impossible, such as black-box membership inference attacks. The trade-off between computational cost and the ability to perform analysis on sensitive models is carefully weighed. The accuracy of the zero-order estimation is analyzed thoroughly within the paper to justify its use in the crucial membership inference task. The effectiveness and reliability of this technique in providing strong empirical results is a major highlight of the paper’s findings.
Privacy & Dataset Size#
The interplay between privacy and dataset size in machine learning is a crucial consideration. Larger datasets generally improve model accuracy, but they also increase the risk of privacy violations. Membership inference attacks (MIAs), which aim to determine if a specific data point was used in training, become more effective with larger datasets. The paper investigates this trade-off by examining input loss curvature, a metric measuring the sensitivity of a model’s loss function to input data. It demonstrates that input loss curvature can effectively distinguish between training and testing data, improving the performance of MIAs. This relationship is further influenced by differential privacy mechanisms implemented during training. Higher privacy parameters (epsilon) constrain model memorization, diminishing the MIAs’ effectiveness. However, the advantage of curvature-based MIAs becomes even more pronounced with sufficiently large datasets, surpassing other methods. Therefore, balancing privacy needs with the benefits of larger training data demands careful attention to both dataset size and the choice of privacy-preserving techniques.
Future Research#
Future research directions stemming from this work could explore more sophisticated zero-order estimation techniques for input loss curvature, potentially improving accuracy and efficiency, especially in black-box settings. Investigating the relationship between input loss curvature and other privacy metrics, such as differential privacy, could yield a more holistic understanding of model privacy. Extending the analysis to different model architectures and datasets would further solidify the findings and demonstrate generalizability. Additionally, exploring ways to leverage input loss curvature for improving model training, such as by using it as a regularization term, could enhance model robustness and privacy simultaneously. Finally, developing novel privacy-preserving techniques that directly address the vulnerability highlighted by curvature-based attacks would be a significant contribution to the field.
More visual insights#
More on figures
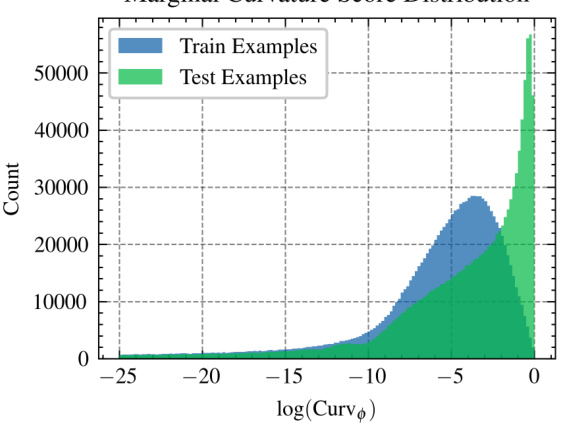
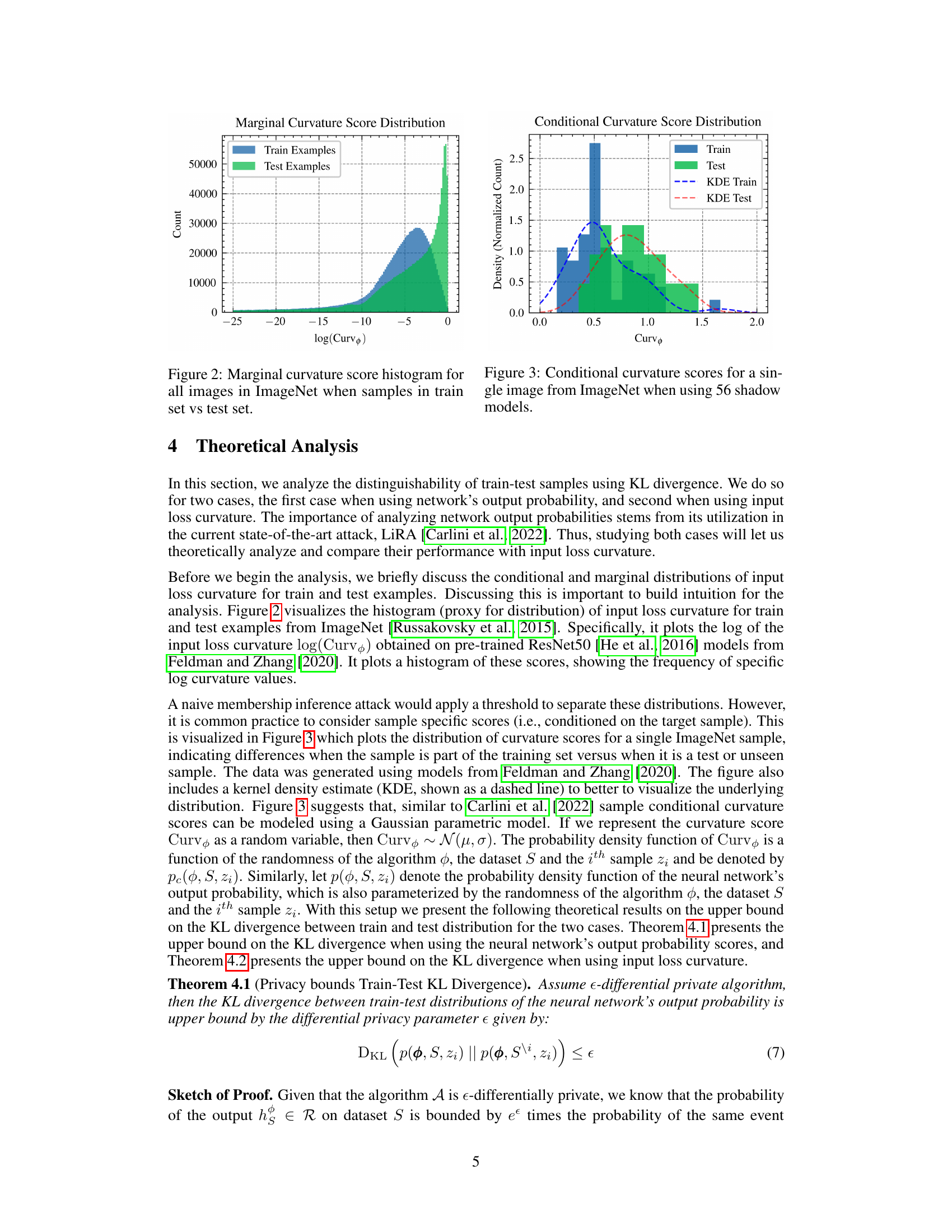
This figure shows the distribution of input loss curvature scores for both training and testing datasets from ImageNet. The x-axis represents the log of the curvature score, and the y-axis represents the count of images. The distribution for the test set is shifted towards higher curvature values (to the right), indicating a difference in curvature between training and testing examples. This difference in curvature is leveraged for membership inference attacks.
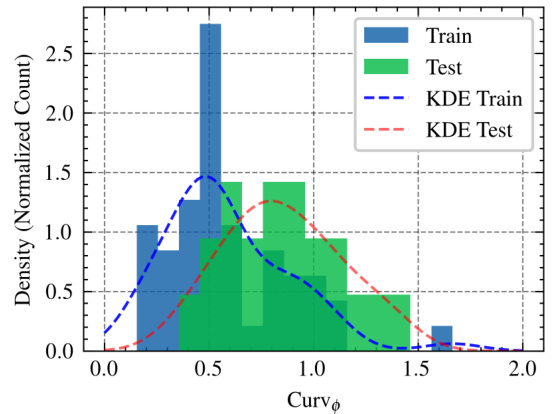
This figure shows the distribution of input loss curvature scores for training and testing samples from the ImageNet dataset. The histogram visually compares the frequency of different curvature values between the train and test sets. The x-axis represents the curvature values, while the y-axis represents the normalized count or frequency. It helps to understand how curvature values differ between the sets that were used to train a model and the set used for testing a trained model.
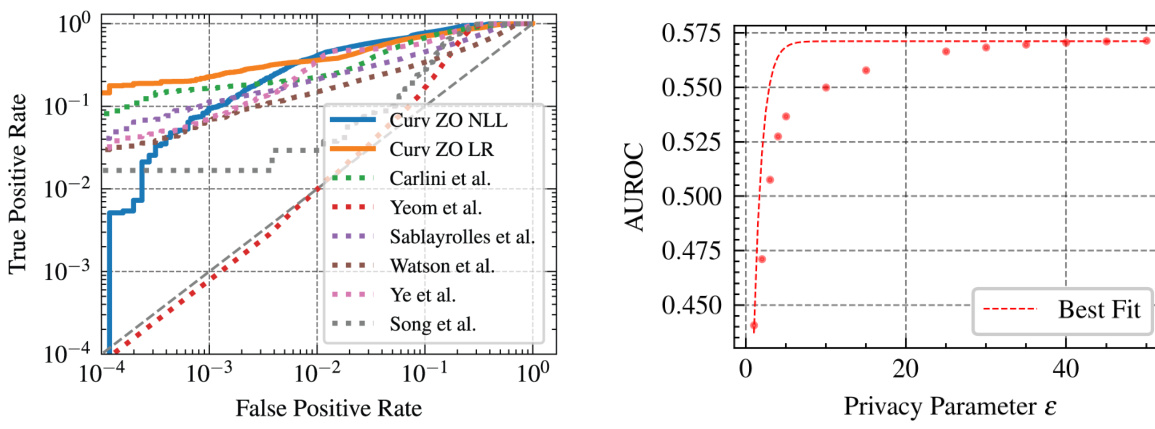
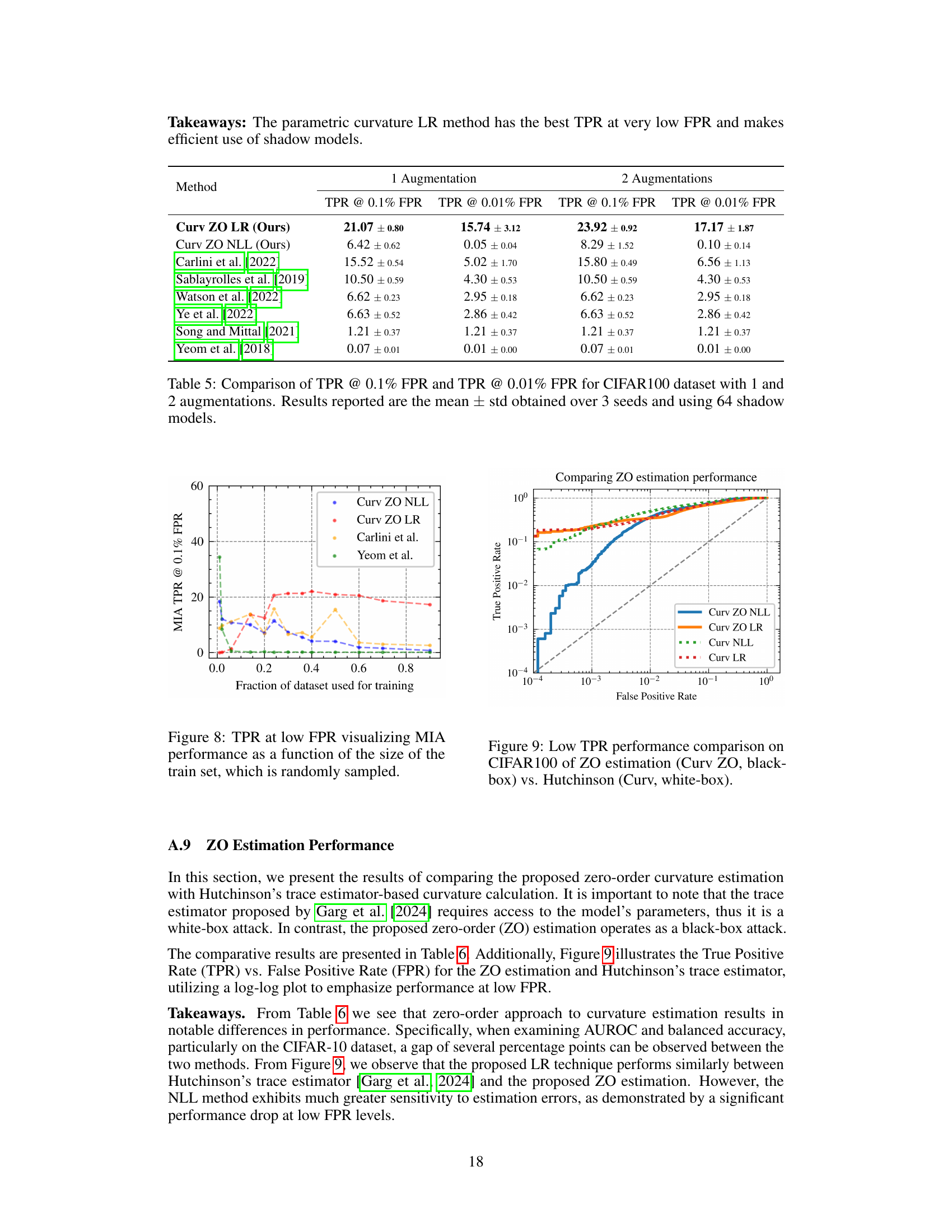
This figure compares the performance of the proposed input loss curvature-based membership inference attack with several existing methods at low false positive rates (FPR). The x-axis represents the false positive rate (FPR), and the y-axis represents the true positive rate (TPR). The plot shows that the proposed parametric Curv LR technique significantly outperforms existing methods, achieving the highest true positive rate at very low false positive rates, indicating its effectiveness in identifying members of the training set even when the allowed error rate is very low.
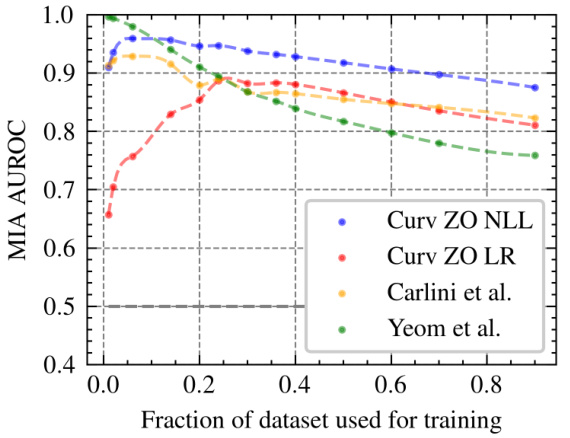
This figure shows how the performance of membership inference attacks (MIAs) changes as the size of the training dataset increases. The x-axis represents the fraction of the dataset used for training, while the y-axis shows the area under the receiver operating characteristic curve (AUROC), a common metric for evaluating the performance of binary classification. The plot compares the AUROC scores of the proposed curvature-based MIA method (‘Curv ZO NLL’ and ‘Curv ZO LR’) with two existing MIA methods (‘Carlini et al.’ and ‘Yeom et al.’). It demonstrates that the performance of the proposed method generally decreases as the fraction of the dataset used for training increases, indicating that larger training sets make it more difficult to accurately determine whether a given data point was used during the training of the model.
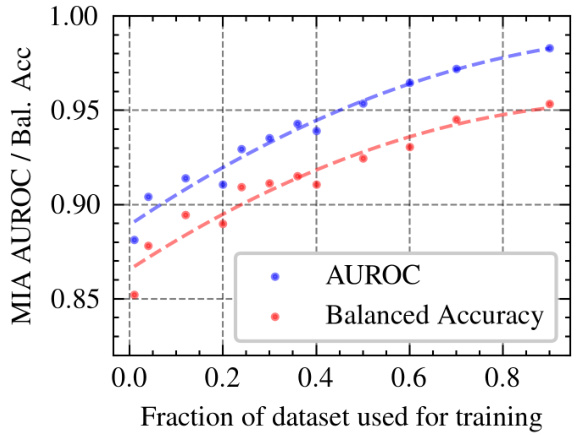
This figure shows how the performance of the membership inference attack (MIA) changes as the size of the training dataset increases. The x-axis represents the fraction of the dataset used for training, ranging from 0 to 0.9. The y-axis represents both the AUROC and the balanced accuracy, which are metrics used to measure the performance of the MIA. The figure includes two lines, one for AUROC (blue circles) and one for balanced accuracy (red circles), showing how each metric changes with the fraction of the training dataset used. The dotted lines represent a trendline showing the general pattern. The figure suggests that as more data is used for training, the performance of the MIA tends to decrease, indicating a potential improvement in privacy with larger training datasets.
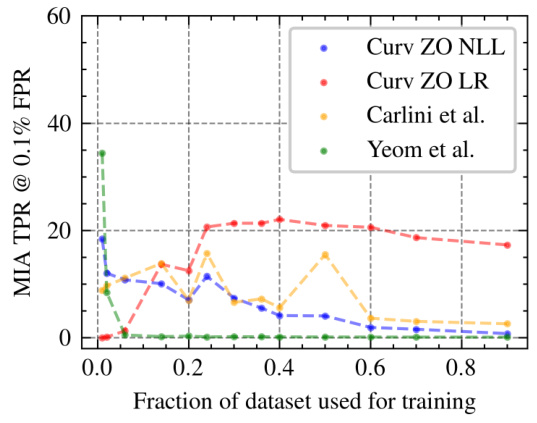
This figure shows how the True Positive Rate (TPR) of different membership inference attack (MIA) methods changes as the size of the training dataset varies. The x-axis represents the fraction of the dataset used for training, while the y-axis shows the TPR at a 0.1% False Positive Rate (FPR). It compares the performance of the proposed curvature-based MIA methods (‘Curv ZO NLL’ and ‘Curv ZO LR’) with existing state-of-the-art methods (‘Carlini et al.’ and ‘Yeom et al.’). The plot illustrates how MIA effectiveness is affected by training set size.

This figure compares the performance of zero-order (ZO) estimation and Hutchinson’s trace estimator for calculating input loss curvature in a membership inference attack. The plot shows the True Positive Rate (TPR) against the False Positive Rate (FPR) on a log-log scale, emphasizing performance at low FPR. The zero-order method is a black-box attack (no model parameters needed), while the Hutchinson method is white-box (requires model parameters). The comparison highlights the differences between the two approaches, particularly at very low FPRs.
More on tables

This table compares the performance of the proposed curvature-based membership inference attack (MIA) with several existing MIA methods on three image datasets: ImageNet, CIFAR100, and CIFAR10. The comparison is done using balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve) metrics. Results are averaged over three different random seeds to provide a measure of stability. The number of shadow models used varies depending on the dataset.
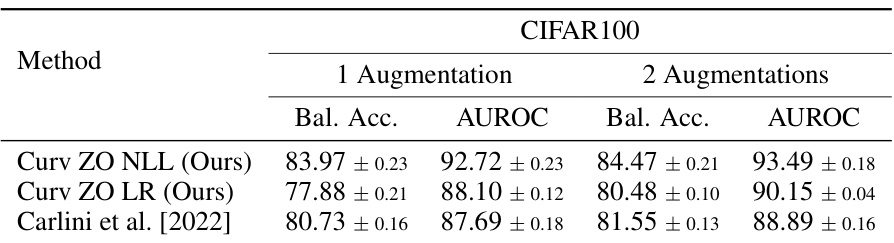
This table compares the performance of the proposed curvature-based membership inference attack (MIA) against several existing MIA methods. The comparison is done across three datasets: ImageNet, CIFAR100, and CIFAR10. Performance is measured using balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve), which are reported as mean ± standard deviation values, averaged over three separate runs with different random seeds. Note that the number of shadow models used varies depending on the dataset.
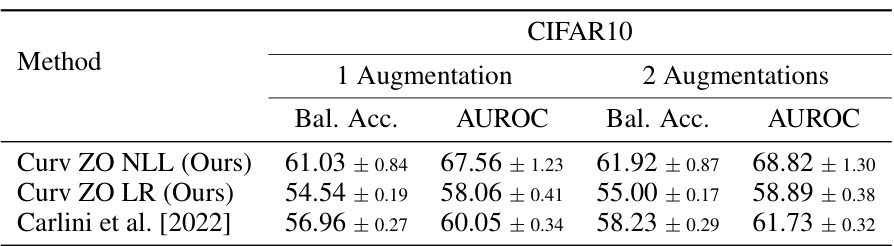
This table presents the performance comparison of the proposed curvature-based membership inference attack (MIA) against existing state-of-the-art methods. It compares the balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve) achieved by the proposed method using zero-order input loss curvature estimation with one augmentation and two augmentations against several other MIA techniques. The results are averaged over three independent runs, and standard deviations are included to demonstrate the stability and reliability of the results. The table provides quantitative metrics to evaluate the effectiveness of the proposed method relative to existing approaches.
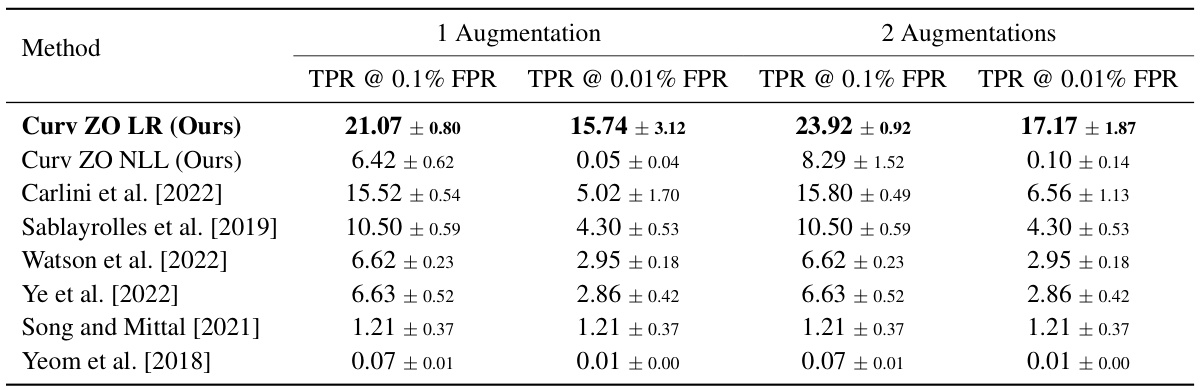
This table compares the performance of the proposed curvature-based membership inference attack (MIA) with several existing MIA methods across three different datasets: ImageNet, CIFAR100, and CIFAR10. The metrics used for comparison are Balanced Accuracy and AUROC, calculated across three separate trials. The number of shadow models employed varies across datasets (64 for CIFAR datasets, 52 for ImageNet).

This table compares the performance of the proposed curvature-based membership inference attack (MIA) with several existing MIA methods. The comparison is done across three datasets: ImageNet, CIFAR100, and CIFAR10. The metrics used for comparison are balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve). The table shows that the proposed method generally outperforms existing methods, particularly on ImageNet.
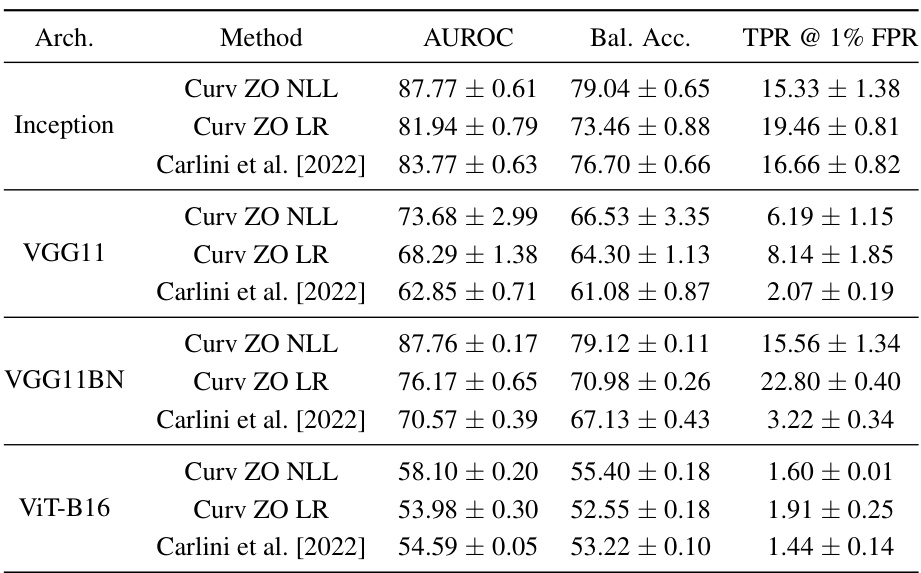
This table compares the performance of the proposed curvature-based membership inference attack (MIA) with several existing MIA methods on three image datasets: ImageNet, CIFAR100, and CIFAR10. The comparison uses balanced accuracy and AUROC (Area Under the Receiver Operating Characteristic curve) as evaluation metrics. Results are averaged over three independent runs with different random seeds. The number of shadow models used in the experiments is also specified.
Full paper#