↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Matrix completion, aiming to recover a complete matrix from incomplete observations, typically assumes data is missing at random. However, real-world data often exhibits informative missingness, where the probability of missingness depends on the unobserved entries themselves, making recovery challenging and potentially biased. Existing methods often struggle with this issue, yielding inaccurate results.
This research introduces a novel pairwise pseudo-likelihood approach to address this challenge. By cleverly using a flexible separable observation probability assumption combined with an exponential family model, the method mitigates bias caused by informative missingness. The researchers prove that their estimator can asymptotically recover the low-rank matrix at a near-optimal rate, and this is validated through numerical experiments demonstrating improved performance compared to existing techniques. This work provides a robust and principled tool for analyzing data affected by informative missingness.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the challenging problem of matrix completion with informative missingness, a common issue in real-world applications where data is often incomplete and the missingness pattern depends on the unobserved values. The proposed method’s robustness and near-optimal convergence rate make it highly relevant to researchers working with incomplete data, opening doors for improved accuracy and reliability in various fields.
Visual Insights#
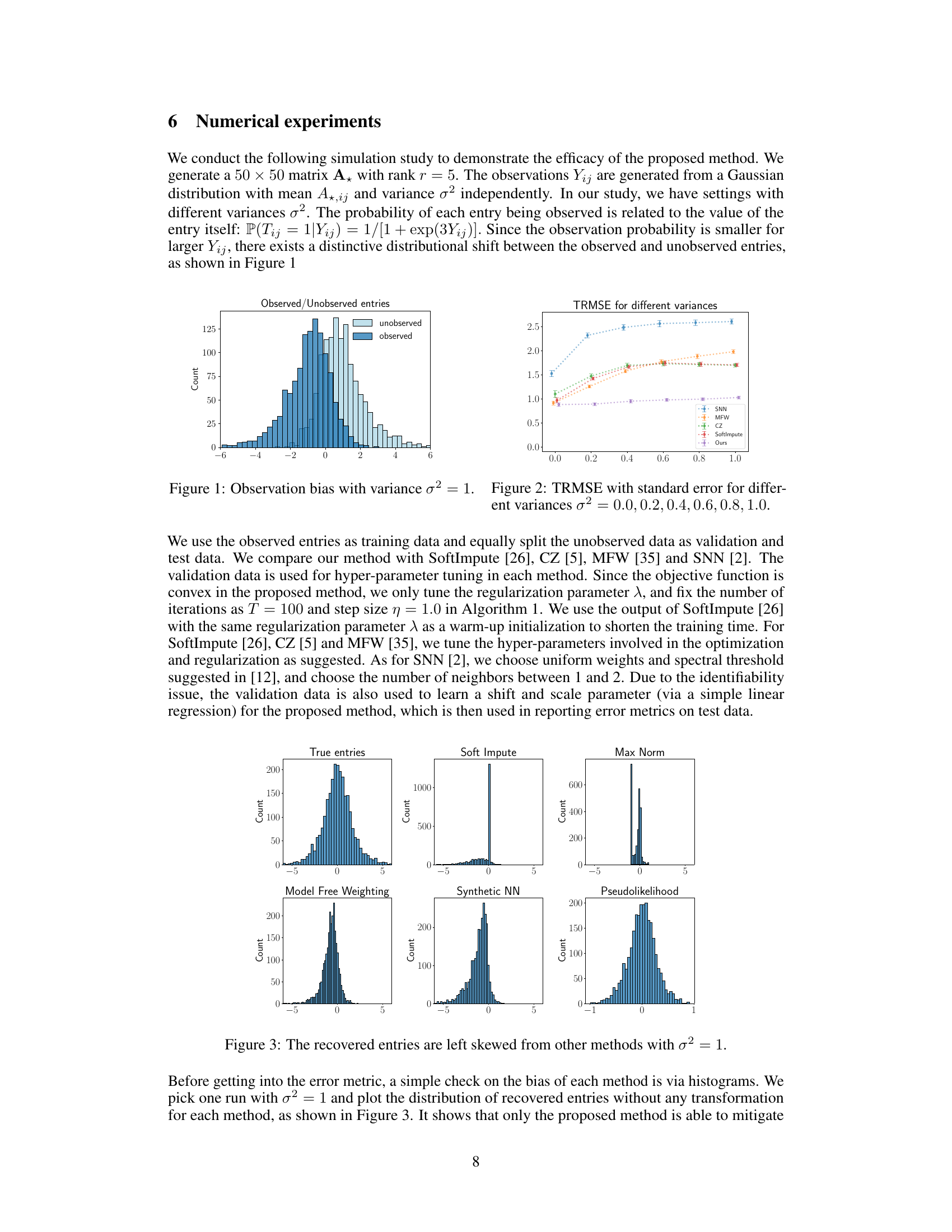
This histogram shows the distributions of observed and unobserved entries in a matrix completion setting where the observation probability depends on the value of the entry itself. Specifically, the probability of observing an entry is 1/[1 + exp(3Yij)], where Yij is the value of the (i,j)th entry. The graph illustrates a clear distributional shift between the observed and unobserved values, indicating informative missingness – the missingness is not at random and depends on the unobserved values. The observed values tend to be clustered closer to zero, while the unobserved values are more dispersed.

This table compares the computational times of different matrix completion methods under the setting of variance σ² = 1. The methods include SoftImpute, Max Norm (CZ), Model Free Weighting (MFW), Synthetic NN (SNN), and the proposed Pseudolikelihood method. The times are reported in seconds, and standard errors are included to reflect variability in runtime.
In-depth insights#
Informative Missingness#
Informative missingness, where the probability of data being missing depends on the unobserved values, poses a significant challenge in matrix completion. Standard missing-at-random assumptions are violated, leading to biased estimators if not properly addressed. The paper tackles this challenge by proposing a regularized pairwise pseudo-likelihood approach. This approach cleverly avoids the need for explicit parametric modeling of the missingness mechanism, offering greater flexibility and robustness. By focusing on pairwise relationships and leveraging local rank statistics, the method effectively mitigates the impact of informative missingness while maintaining a near-optimal convergence rate. The key innovation lies in its ability to identify the low-rank parameter matrix up to a constant shift and scaling, despite the inherent identifiability issues of informative missingness. Numerical experiments demonstrate the efficacy of the approach, particularly in settings with high variance and non-uniform observation probabilities, showcasing its potential as a powerful tool in matrix completion. The use of the exponential family model further enhances the method’s flexibility, enabling application to various data types beyond just Gaussian data.**
Pairwise Pseudo-likelihood#
The pairwise pseudo-likelihood approach, as presented in the context of matrix completion with informative missingness, offers a compelling alternative to traditional likelihood-based methods. Its robustness stems from circumventing the need to explicitly model the complex, often intractable, missing data mechanism. Instead, it leverages a flexible, separable observation probability assumption, enabling the identification of the low-rank parameter matrix (up to an identifiable equivalence class) even when missingness depends on unobserved values. This method utilizes local ranks of observations, computationally avoiding the intractable full-rank likelihood calculations. A key strength is its asymptotic convergence rate nearing the optimal rate seen in standard, well-posed scenarios. The use of regularization (nuclear norm and entry-wise max norm) further enhances the estimator’s robustness and low-rank structure. However, a careful analysis of identifiability issues is crucial, as scale and shift equivalences exist. Despite these limitations, the approach demonstrates promising empirical performance, effectively mitigating data bias introduced by informative missingness in various real-world datasets. The overall strategy positions pairwise pseudo-likelihood as a valuable and versatile tool in the matrix completion field, particularly when dealing with complex missing data patterns.
Identifiability Issues#
In the context of matrix completion with informative missingness, identifiability issues arise because the missing data mechanism depends on the unobserved entries of the matrix, making it difficult to uniquely recover the true matrix. This non-identifiability is inherent to the problem and not an artifact of any specific estimation method. The paper addresses this by imposing a separable informative missingness assumption. This assumption, while restrictive, allows for identification of the matrix up to a constant shift and scaling, preserving valuable information like relative rankings of entries, important in applications like recommender systems. The scale-shift equivalence highlights the inherent ambiguity, emphasizing that precise recovery is impossible without additional assumptions or constraints. Therefore, the focus shifts to identifying a representative within this equivalence class that achieves the best performance and mitigating the effects of the inherent ambiguity. The paper demonstrates that their proposed pairwise pseudo-likelihood approach effectively mitigates the impacts of informative missingness while achieving a near-optimal convergence rate under the assumed conditions.
Near-Optimal Convergence#
The concept of “Near-Optimal Convergence” in the context of a matrix completion research paper signifies that the proposed algorithm achieves a convergence rate very close to the best possible rate (optimal rate) achievable under ideal conditions. This is a crucial finding, demonstrating the algorithm’s efficiency. It suggests that the algorithm’s performance isn’t significantly hampered by the complexities introduced, such as non-uniform or informative missingness. The claim of near-optimality is typically backed by theoretical analysis which compares the algorithm’s convergence rate to known lower bounds derived from information theory or statistical learning theory. Achieving near-optimal convergence is highly desirable because it means the algorithm efficiently extracts the underlying information from the data even with significant challenges presented by missing data patterns. However, it is crucial to carefully examine the assumptions made in proving near-optimality as these might limit the applicability of the result in practice. For example, certain assumptions about the noise distribution or the underlying low-rank structure of the matrix might be violated in real-world applications. The practical implications are substantial as near-optimal convergence often translates into faster processing, improved accuracy, and robustness to noise and data irregularities.
Robustness & Bias#
A robust model should demonstrate resistance to noise and outliers while minimizing bias. The paper’s approach to matrix completion, using a pairwise pseudo-likelihood method, is presented as robust. This robustness stems from its ability to handle informative missingness, a significant departure from traditional missing-at-random assumptions. The flexible observation probability model, coupled with the exponential family data model, expands applicability to various real-world scenarios. However, identifiability issues are explicitly acknowledged, particularly regarding the non-identifiability of a constant shift in the matrix. This limitation might introduce a certain degree of bias in the estimation. The theoretical guarantee section provides a convergence rate analysis, revealing how the proposed method mitigates bias despite identifiability constraints, achieving near-optimal rates for the well-posed case. This theoretical support is augmented by numerical experiments that illustrate the efficacy of the method in mitigating data bias and comparing its performance to alternative methods, especially when there’s a substantial distributional shift between observed and unobserved entries.
More visual insights#
More on figures
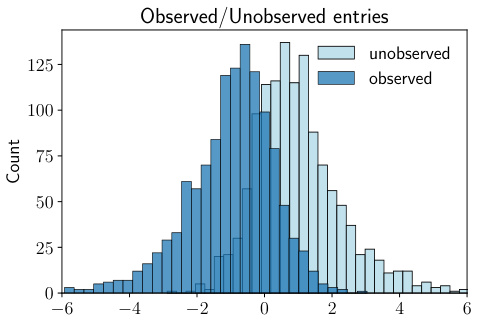
The figure shows the test root mean squared errors (TRMSE) with standard errors for different variances (σ² = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0). The TRMSE is a measure of the error in recovering the matrix. The plot compares the performance of the proposed method against four other matrix completion methods: SoftImpute, CZ, MFW, and SNN. The results indicate the relative performance of each method at different noise levels. As the variance increases, the error for all methods also increases, but the proposed method maintains comparatively lower error.
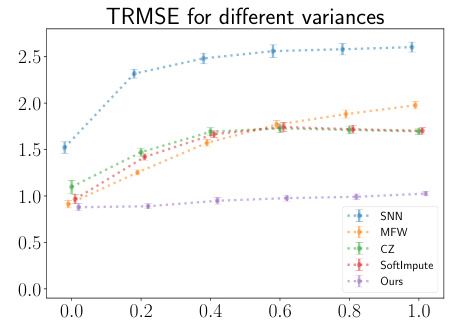
This figure shows histograms of the recovered entries for different matrix completion methods when the true data has a variance of 1. The ‘True entries’ histogram displays a near-symmetric distribution. However, the histograms for the SoftImpute, Max Norm, Model Free Weighting, and Synthetic NN methods all exhibit left skewness, while the Pseudolikelihood method shows a near-symmetric distribution, indicating that it is able to mitigate the left-skewness observed in the other methods.
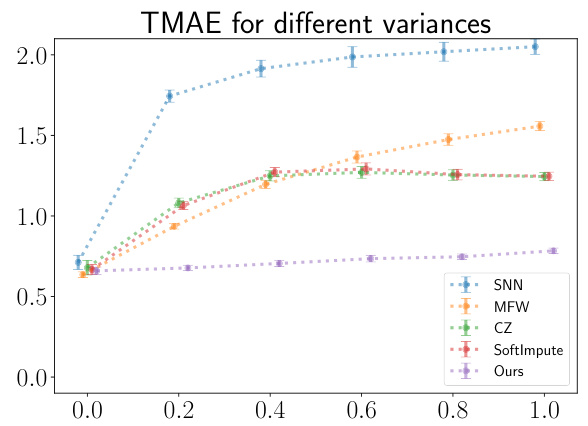
The figure shows the test mean absolute errors (TMAE) for different variance settings (σ² = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0). Each point represents the average TMAE across multiple runs of the experiment, and the error bars indicate the standard error of the mean. The plot compares the performance of five different matrix completion methods: SoftImpute, CZ, MFW, SNN, and the proposed pairwise pseudo-likelihood method. The results are useful to show the efficacy of different methods under different noise levels.
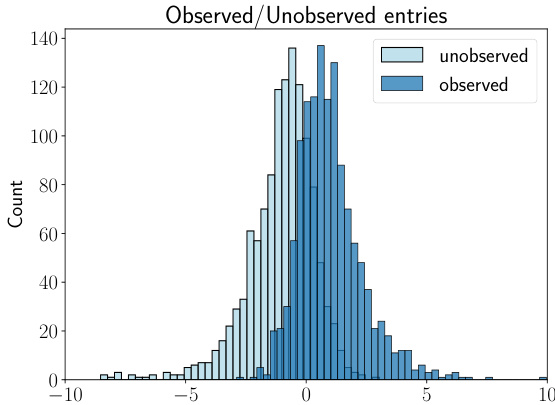
This histogram shows the distributions of observed and unobserved matrix entries. The data is generated from a Gaussian distribution with a mean equal to the true matrix entry and variance σ² = 1. The probability of observing an entry depends on its value according to P(Tij = 1|Yij) = 1/[1 + exp(3Yij)]. The figure highlights a clear distributional shift between observed (blue) and unobserved (light blue) entries, demonstrating the informative missingness in the data.
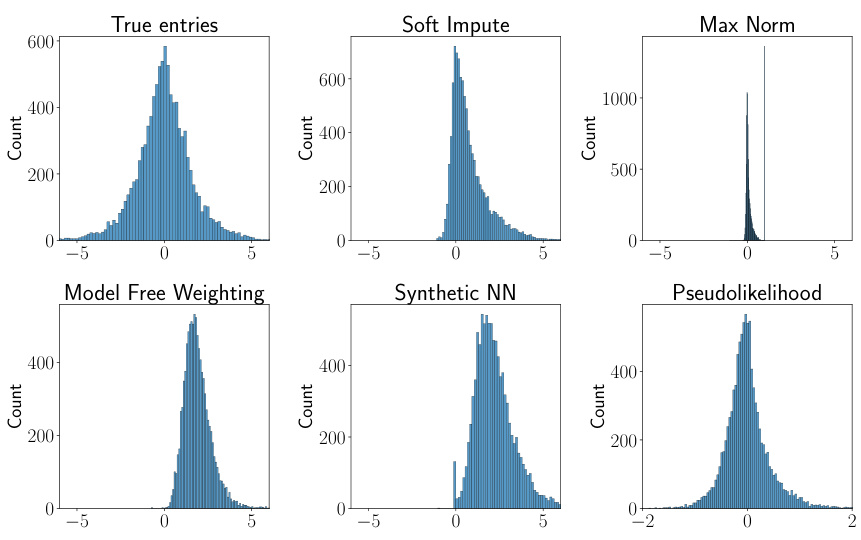
The figure shows histograms of the recovered entries using different matrix completion methods when the true entries’ variance is 1. The histogram for the proposed Pseudolikelihood method shows a distribution close to the symmetric distribution of the true entries. In contrast, the histograms for the other methods (Soft Impute, Max Norm, Model Free Weighting, and Synthetic NN) show left-skewed distributions, indicating that these methods are biased and are not able to recover the true distribution of the data well in this case.
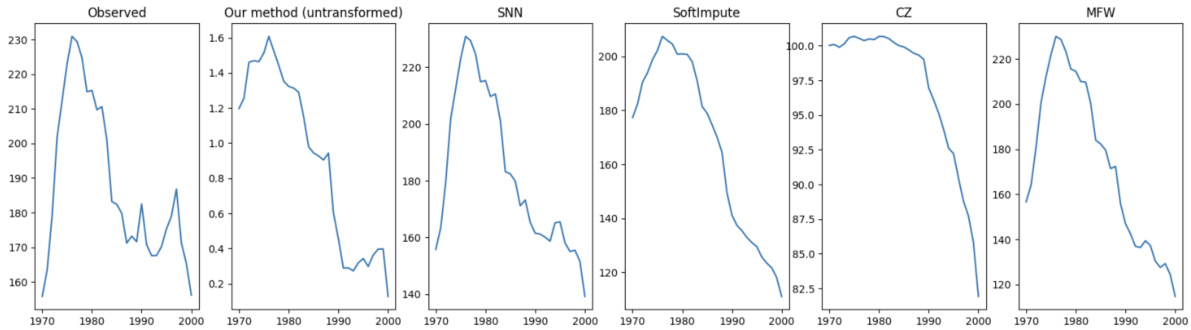
This figure compares the observed sales data for State KS over 30 years with the sales predicted by five different matrix completion methods: the proposed method, SNN, SoftImpute, CZ, and MFW. The first plot displays the observed sales trend, while the remaining plots illustrate the sales predictions generated by each method. Note that the proposed method’s prediction is presented in its untransformed form to highlight the trend.
More on tables
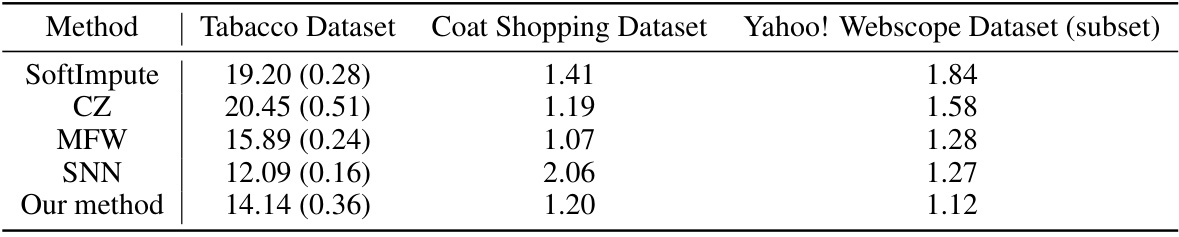
This table shows the test root mean squared errors (TRMSE) achieved by different matrix completion methods on three real-world datasets: Tobacco Dataset, Coat Shopping Dataset, and Yahoo! Webscope Dataset. For the Tobacco dataset, the average TRMSE across 100 simulations with randomly generated missing data is reported along with standard errors. The results highlight the performance of each method on datasets with different characteristics and missing data patterns.

This table presents the test root mean squared errors (TRMSE) for three datasets: Tobacco, Coat Shopping, and Yahoo! Webscope. The Tobacco dataset results are averages across 100 simulations with standard errors reported. The other two datasets have a single TRMSE reported for each method.

The table presents the test root mean squared error (TRMSE) for three different datasets: Tobacco Dataset, Coat Shopping Dataset, and Yahoo! Webscope Dataset. For the Tobacco dataset, the average TRMSE across 100 simulations is reported with standard errors. The results show the performance of different matrix completion methods on these datasets, indicating their relative effectiveness in handling missing data.
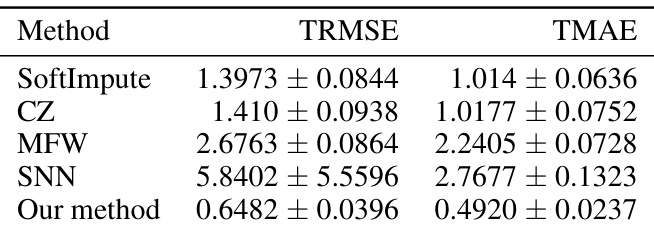
This table presents the results of a simulation study comparing the performance of five different matrix completion methods, including the proposed method, on a dataset with informative missingness. The methods are evaluated using two common metrics: Test Root Mean Squared Error (TRMSE) and Test Mean Absolute Error (TMAE). The results show the mean error and its standard deviation across multiple runs of the experiment. The proposed method demonstrates superior performance compared to other approaches.
Full paper#