↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Decision Transformers (DTs) are a promising paradigm in offline reinforcement learning, but their online finetuning remains under-explored. Existing methods like Online Decision Transformer (ODT) struggle with low-reward offline data. This paper theoretically analyzes the limitations of ODT’s online finetuning process, attributing the issues to the use of Return-To-Go (RTG) far from the expected return.
The paper proposes a novel method that integrates TD3 gradients into the ODT’s online finetuning process. This simple yet effective approach significantly enhances ODT’s performance, particularly when pretrained on low-reward data. Experiments across multiple environments confirm the effectiveness of adding TD3 gradients, demonstrating improvements in online performance compared to the baseline ODT and other offline RL algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning, particularly those working with decision transformers. It addresses a significant gap in the current literature by focusing on online finetuning of these models. The findings demonstrate a practical approach for enhancing performance, particularly when dealing with low-reward offline data. This is highly relevant to current research trends focusing on data efficiency and offline-to-online RL. The work opens up new avenues for improving decision transformers by integrating RL gradients and suggests further exploration into the theoretical aspects of online finetuning.
Visual Insights#
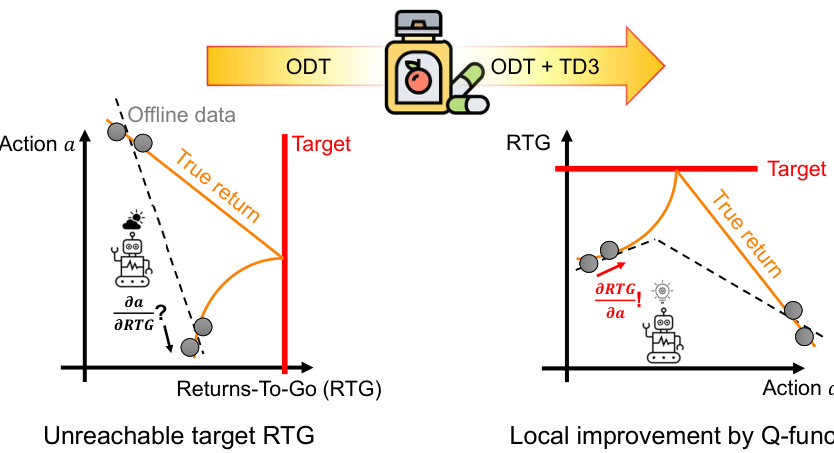
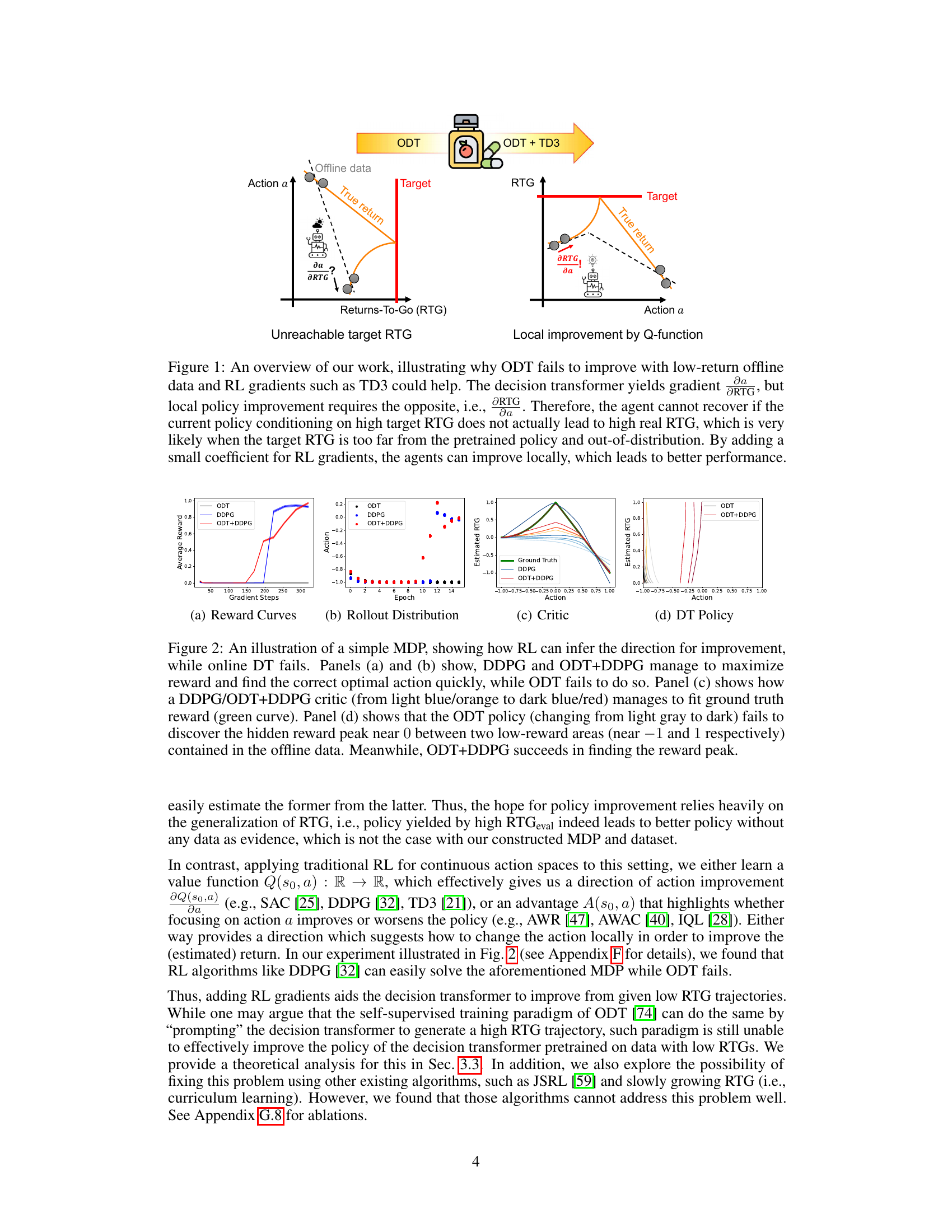
This figure illustrates the core idea of the paper. On the left, it shows how the Online Decision Transformer (ODT) struggles when pretrained with low-reward offline data. The ODT’s policy gradient (∂RTG/∂a) is in the opposite direction needed for improvement in this scenario. The unreachable target RTG makes it difficult to recover. The right side of the figure demonstrates the proposed solution which adds reinforcement learning (RL) gradients (TD3). This allows for local policy improvements by providing the needed ∂RTG/∂a for improvement, leading to better overall performance.
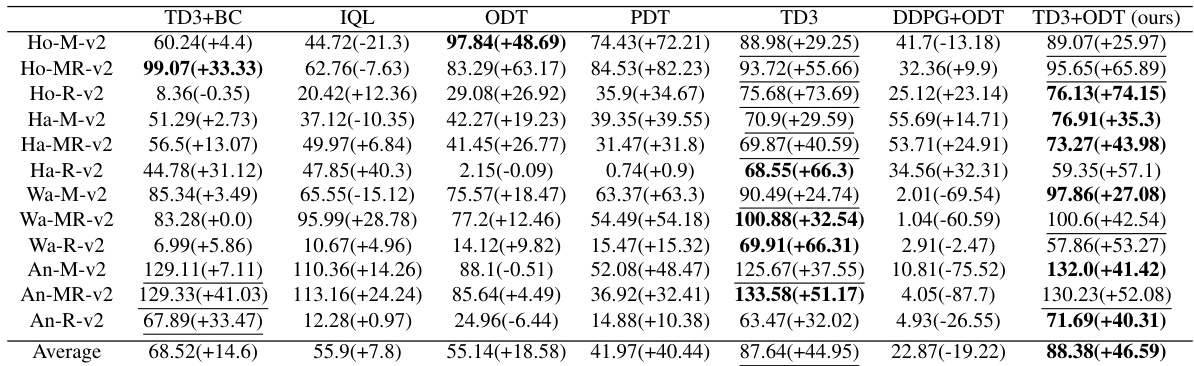
This table presents the average reward achieved by different methods on various MuJoCo environments before and after online finetuning. The best performing method for each environment is highlighted in bold, and any result within 90% of the best is underlined. Environment and dataset names are abbreviated for space-saving.
In-depth insights#
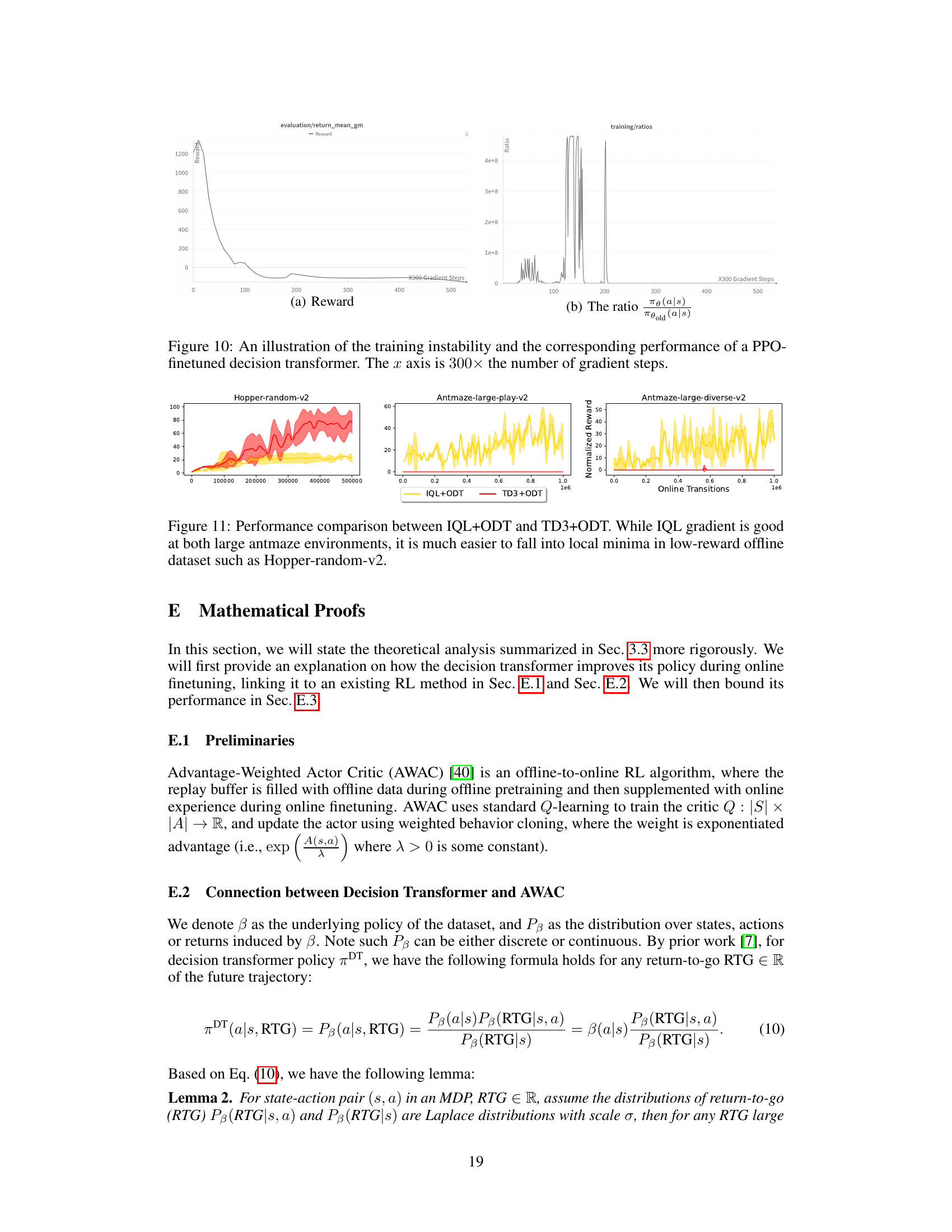
ODT’s Online Tuning#
ODT’s online tuning, a crucial aspect of its performance, focuses on adapting the pre-trained model to new, online data. The core idea is to continue the supervised learning paradigm used in offline training, iteratively updating the model with newly collected trajectories. However, a critical limitation emerges when the offline data used for pre-training is of low reward quality. This leads to difficulties in effective online finetuning since the initial policy struggles to improve upon suboptimal trajectories. A proposed solution involves adding reinforcement learning gradients from algorithms like TD3 to the online fine-tuning process. This addition helps steer the policy towards local improvements that are otherwise missed by solely relying on the supervised learning signal. This approach is particularly effective when overcoming the limitations associated with low-reward offline data pre-training, demonstrating an improvement in online performance. Further investigation is needed to explore the reasons behind these observed improvements and analyze the overall efficacy of the combined approach. Future research could focus on resolving the limitations of the theoretical analysis presented in this method, potentially via relaxation of assumptions for a wider applicability and robust generalization.
RL Gradient Boost#
The concept of “RL Gradient Boost” in the context of reinforcement learning (RL) suggests enhancing the training process by incorporating gradients derived from standard RL algorithms. This approach directly addresses the limitations of solely relying on supervised learning methods for fine-tuning decision transformers, particularly when dealing with low-reward offline datasets. By integrating RL gradients, the method aims to refine the policy by leveraging both supervised and reinforcement learning signals. This combined approach likely leads to more robust and efficient online fine-tuning, overcoming the challenge of suboptimal trajectories often encountered in traditional offline-to-online RL paradigms. The boost is particularly significant when the model is pretrained on low-reward data, indicating that the RL gradients serve as a corrective mechanism, steering the policy towards better performance in online scenarios. This approach represents a novel integration of supervised and RL methods, potentially offering a substantial improvement over purely supervised techniques in online RL tasks with decision transformers.
Theoretical Analysis#
A theoretical analysis section in a reinforcement learning research paper would ideally delve into the mathematical underpinnings of the proposed methods. It might start by formally defining the problem within a Markov Decision Process (MDP) framework. Key aspects like the state and action spaces, reward functions, and transition probabilities would be explicitly stated, along with assumptions made for tractability. The core of the analysis would then focus on deriving key properties of the proposed algorithm, potentially proving its convergence, optimality, or sample complexity under certain conditions. For instance, a proof of convergence might demonstrate that the algorithm’s parameters converge to an optimal policy over time. Another key aspect may be to mathematically characterize the relationship between the model’s performance and the characteristics of the training data, such as the quality or quantity of data available. A particularly insightful theoretical analysis might identify potential limitations of the proposed algorithm. This could involve proving bounds on its performance, highlighting scenarios where it might fail to achieve optimal solutions, or demonstrating its sensitivity to specific hyperparameters or data distributions. The analysis may use tools from probability theory, statistics, optimization, and information theory to prove the claims made. Finally, the analysis may offer novel insights or theoretical connections to existing work in reinforcement learning, placing the presented methods within a broader context and demonstrating their novelty and significance.
Empirical Findings#
An Empirical Findings section in a research paper would present results from experiments or observations designed to test the hypotheses. It should begin with a clear and concise summary of the main findings, highlighting any statistically significant results. Visualizations such as graphs and tables are crucial for effectively presenting complex data, enhancing understanding and supporting claims. The discussion should explicitly address whether the results support or refute the initial hypotheses. A detailed analysis of potential confounding variables and limitations of the methodology is necessary to ensure the reliability and validity of the conclusions. Crucially, any unexpected or surprising results should be noted and potential explanations offered. This section’s strength lies in its clarity, depth of analysis, and transparency regarding limitations and potential biases. The findings should be directly connected to the paper’s broader contributions, clearly showing how they advance the field of study.
Future Work#
The paper’s “Future Work” section presents exciting avenues for expanding upon the core findings. Addressing the limitations of the theoretical analysis, specifically relaxing assumptions made about reward distributions and incorporating more realistic noise models, is crucial for broader applicability. Exploring alternative RL gradient methods beyond TD3, potentially incorporating algorithms better suited to high-dimensional action spaces, or examining hybrid approaches that combine different RL techniques, could yield significant performance improvements. Investigating the impact of different architectural choices for both the decision transformer and the critic network, including exploring more advanced transformer architectures or value function approximators, is also warranted. Finally, a thorough exploration of different training paradigms beyond the supervised learning framework employed here could unlock new capabilities, especially in handling out-of-distribution data in real-world settings.
More visual insights#
More on figures
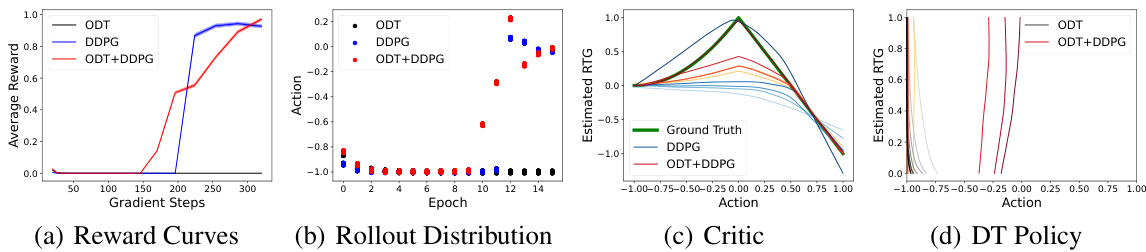
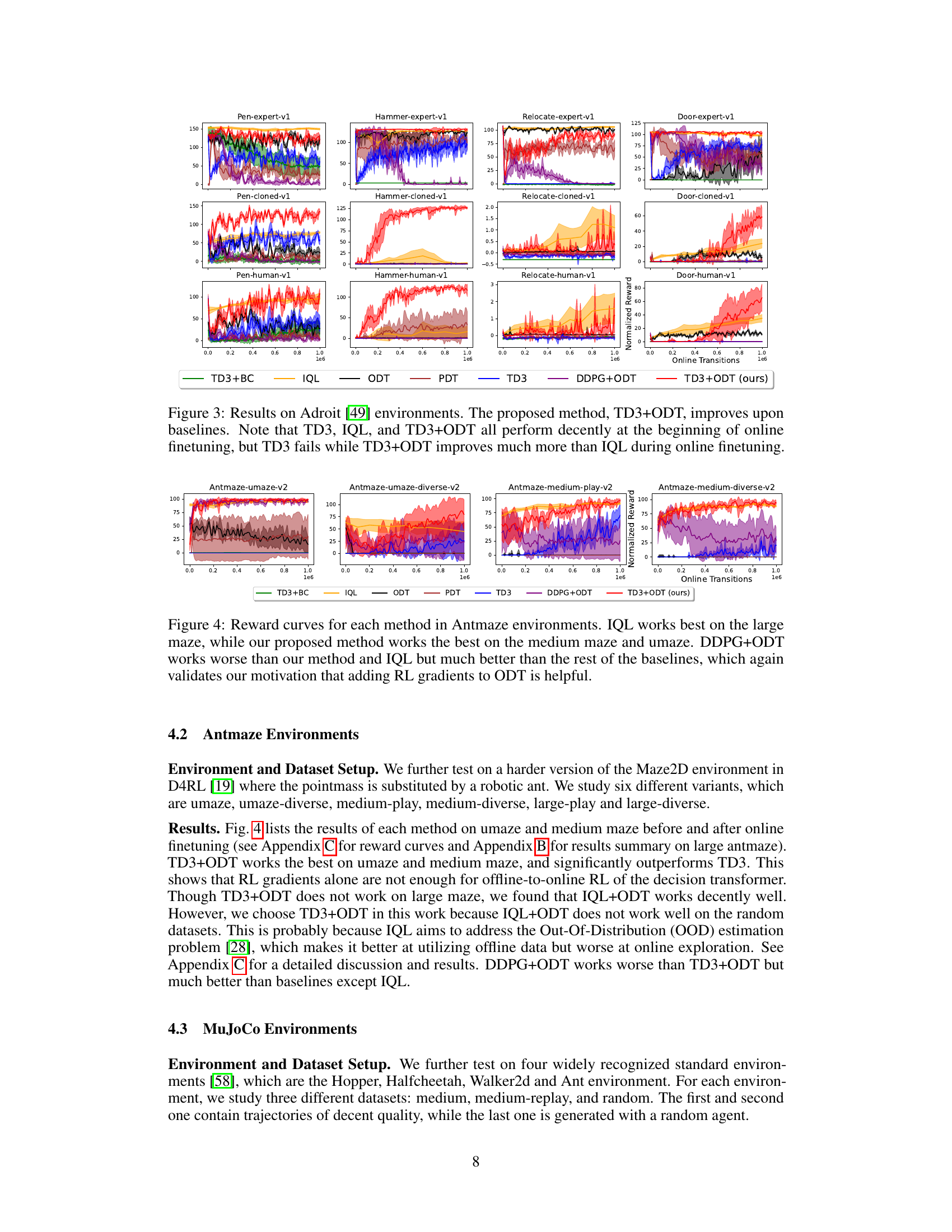
This figure demonstrates the effectiveness of RL gradients in online finetuning of decision transformers by comparing DDPG, ODT, and ODT+DDPG on a simple MDP. It shows that DDPG and ODT+DDPG quickly learn the optimal action and maximize reward, unlike ODT. The critic plots demonstrate that DDPG and ODT+DDPG accurately learn the reward function, while ODT fails to identify a hidden reward peak.
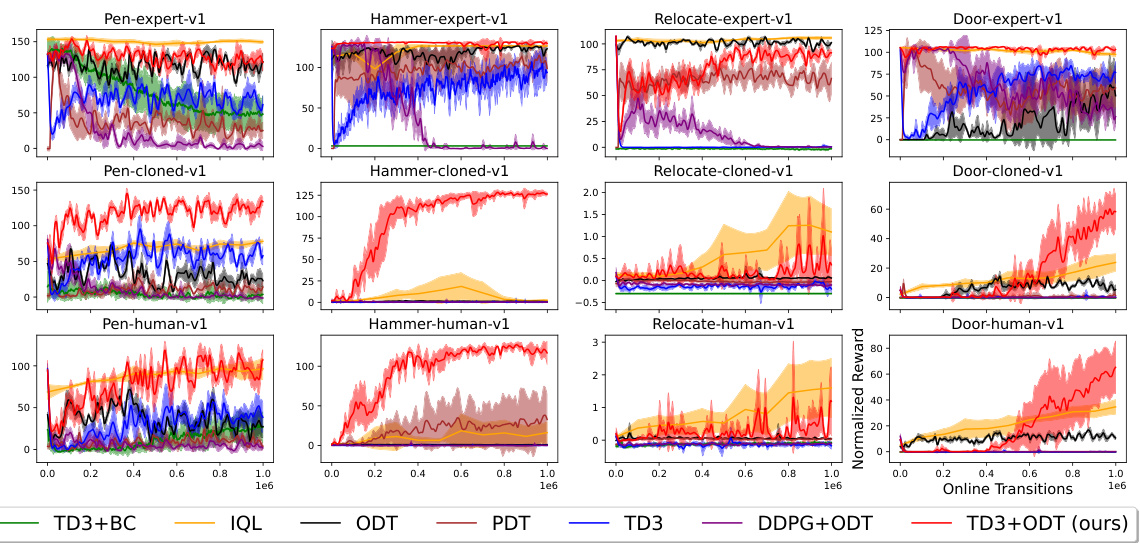
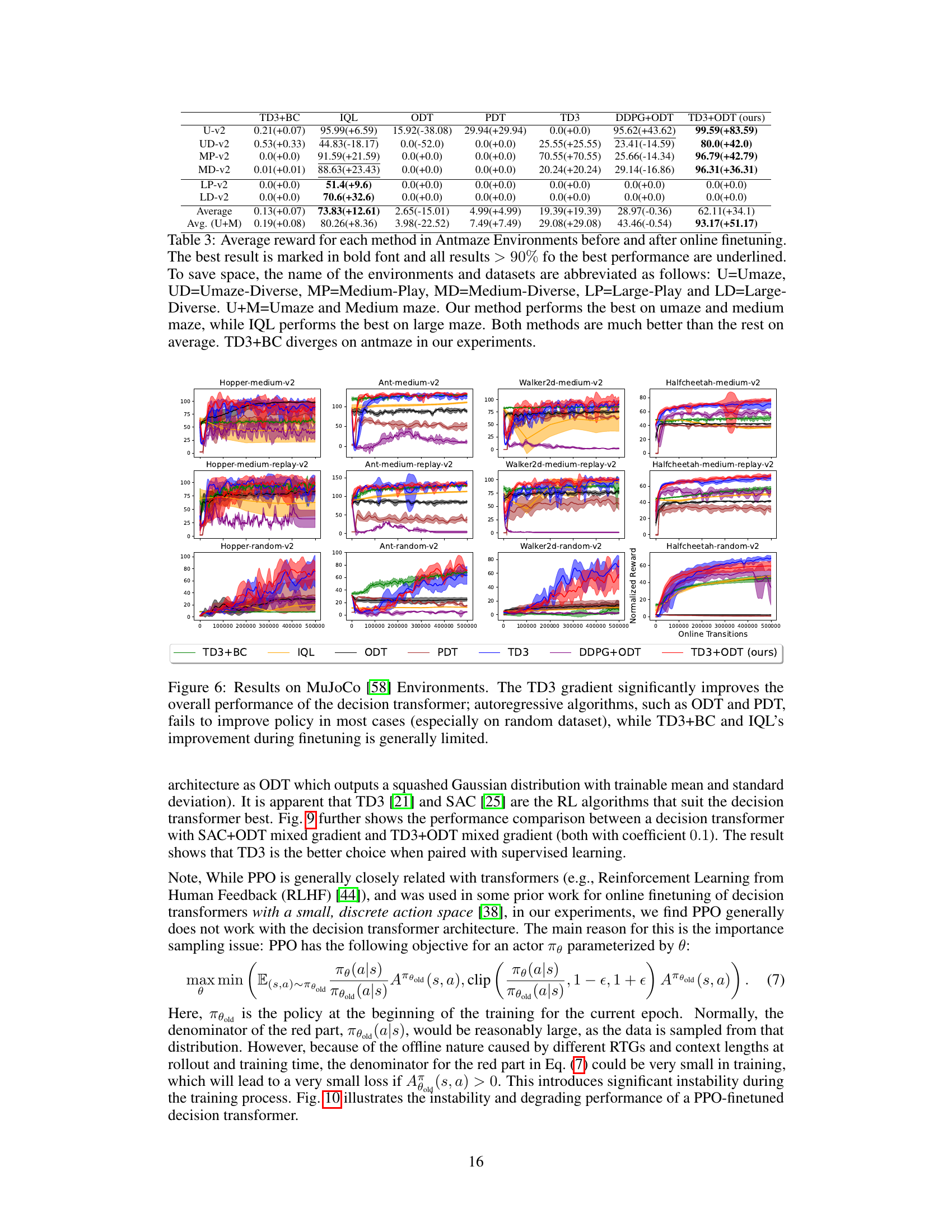
This figure shows the performance comparison of different methods on four Adroit environments (Pen, Hammer, Door, Relocate) with three different datasets (expert, cloned, human). The results indicate that TD3+ODT consistently outperforms other baselines, including ODT, PDT, TD3, DDPG+ODT, and TD3+BC. While TD3, IQL, and TD3+ODT show decent initial performance, TD3 shows instability during online finetuning, whereas TD3+ODT demonstrates significant improvement compared to IQL. The figure highlights the superiority of TD3+ODT, particularly when pretrained with low-reward offline data.

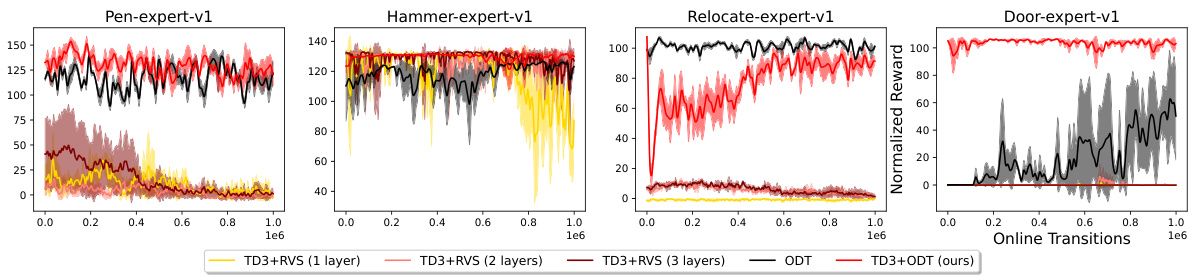
This figure shows the performance comparison of different methods on four robotic manipulation tasks from the Adroit environment. Each task uses three different datasets: expert, cloned, and human. The results indicate that the proposed method (TD3+ODT) outperforms other baselines, especially during online fine-tuning. While TD3, IQL, and TD3+ODT show decent initial performance, TD3 struggles later, whereas TD3+ODT significantly surpasses IQL’s improvement.

This figure presents ablation studies on two hyperparameters: the RL coefficient α and the evaluation context length Teval. Panel (a) shows how varying α affects the performance on two different environments, highlighting the trade-off between improved exploration and potential instability. Panel (b) demonstrates the impact of Teval on performance, illustrating the balance between utilizing sufficient contextual information and maintaining stable training. The results suggest that carefully tuning these hyperparameters is crucial for optimal performance.
This figure presents the results of the proposed method (TD3+ODT) and several baseline methods on four Adroit robotic manipulation tasks. Each task involves three different datasets: expert, cloned, and human. The plots display the average normalized rewards over time for each method. The results show that the TD3+ODT method consistently outperforms the baseline methods, especially in the online finetuning phase (when the policy is updated using online data collected from the environment). While methods like TD3 and IQL achieve decent performance initially, they struggle to consistently improve during online finetuning. In contrast, TD3+ODT shows greater and more consistent gains in performance, indicating the effectiveness of adding TD3 gradients to the online finetuning of decision transformers.
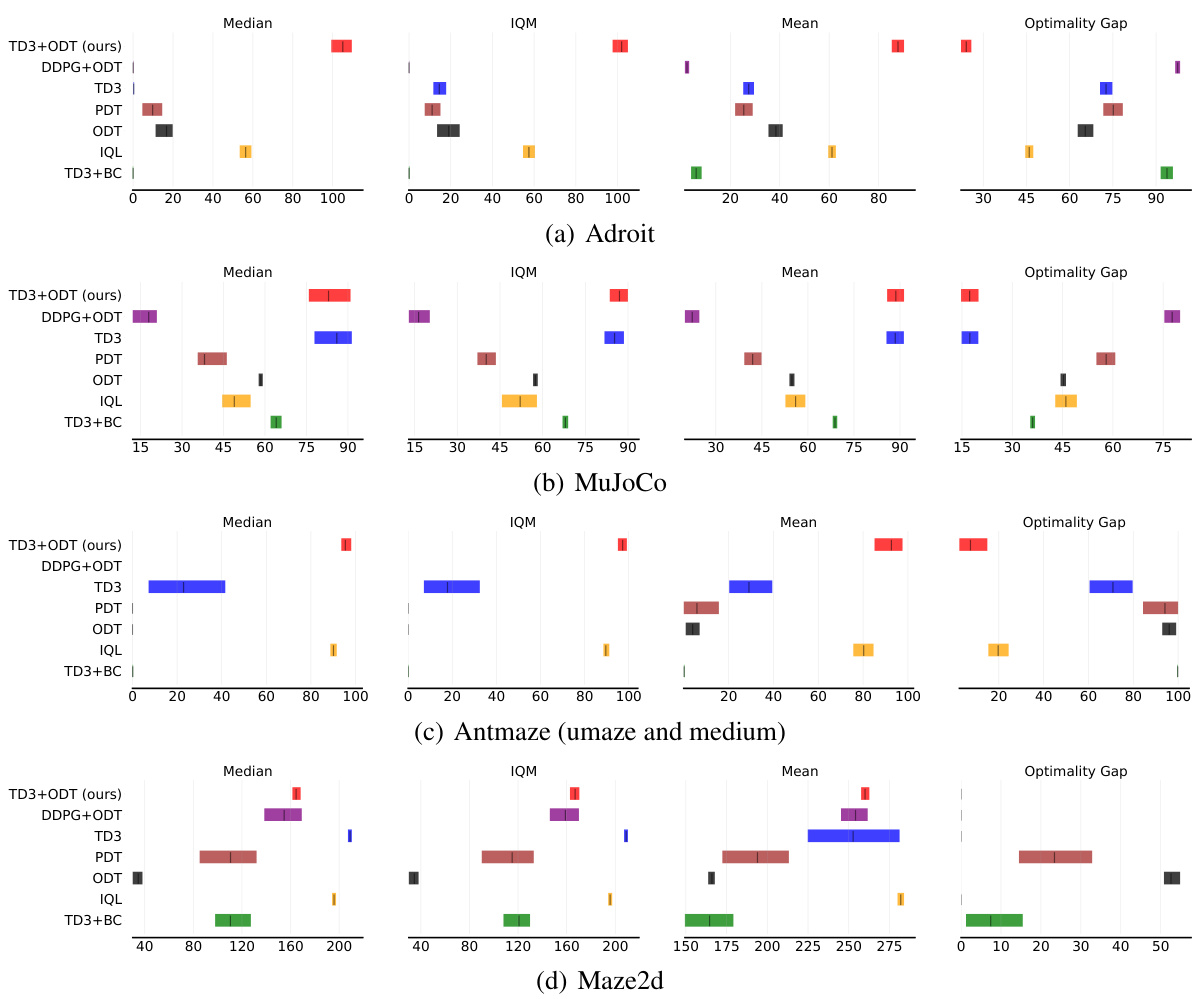
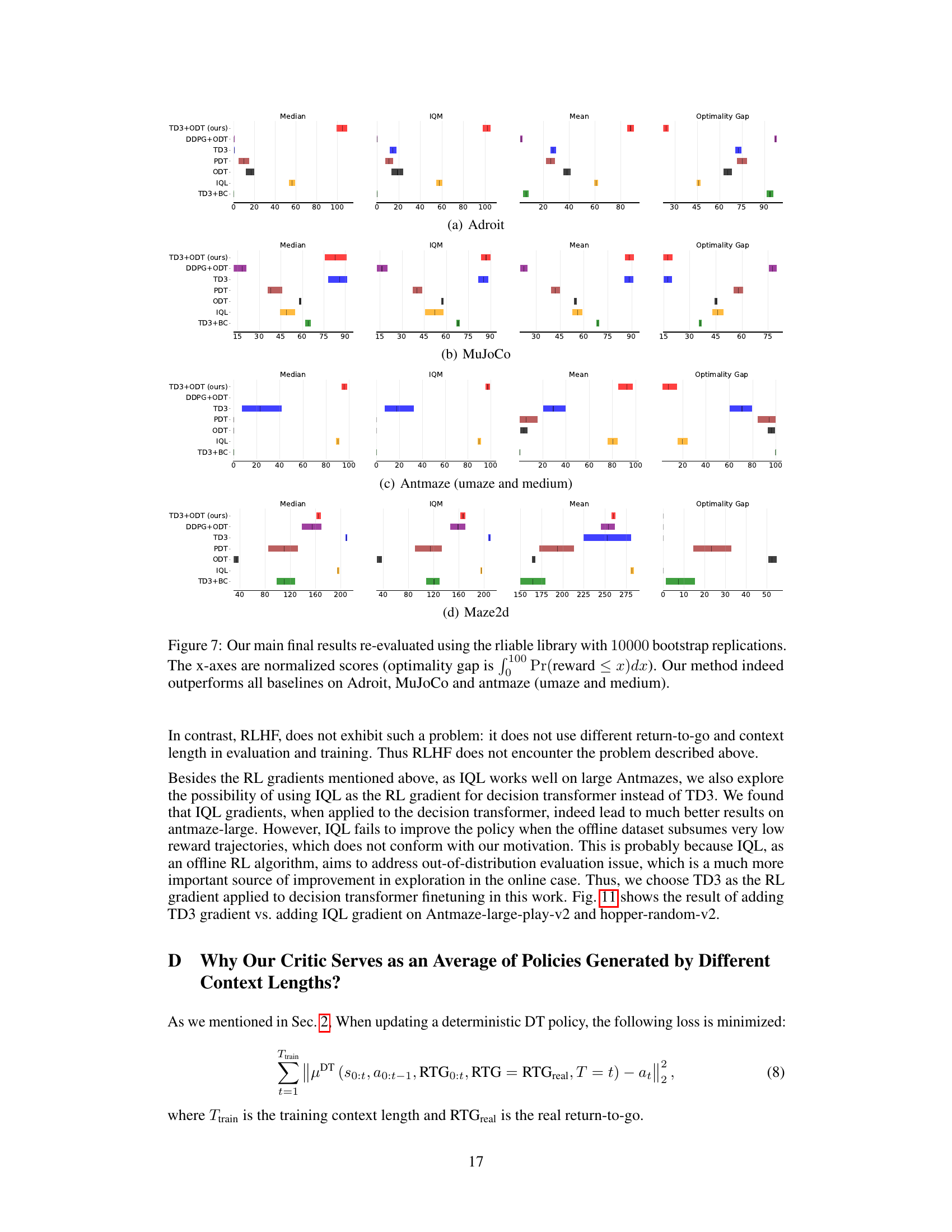
This figure displays the results of the experiments using the rliable library, which provides more robust statistical analysis compared to simply using the average reward. The results are presented for four environments (Adroit, MuJoCo, Antmaze umaze, and Antmaze medium), each showing median, interquartile mean (IQM), mean, and optimality gap across multiple runs, highlighting the improved performance of TD3+ODT over other baselines.
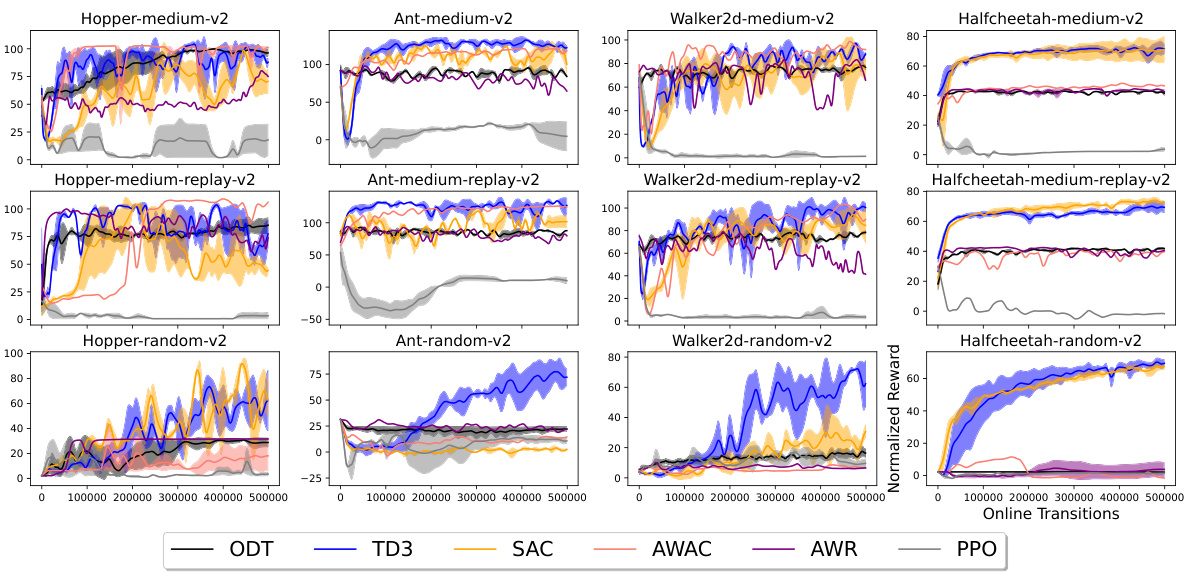
This figure shows the performance of different algorithms on four robotic manipulation tasks from the Adroit environment. The x-axis represents the number of online transitions (interactions with the environment during fine-tuning), and the y-axis shows the normalized average reward. Seven methods are compared: TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT (the proposed method). The figure shows that TD3+ODT consistently outperforms the baselines, especially when pre-training data has low reward. While TD3, IQL, and TD3+ODT all perform reasonably well initially, TD3’s performance degrades during online finetuning, whereas TD3+ODT significantly improves.
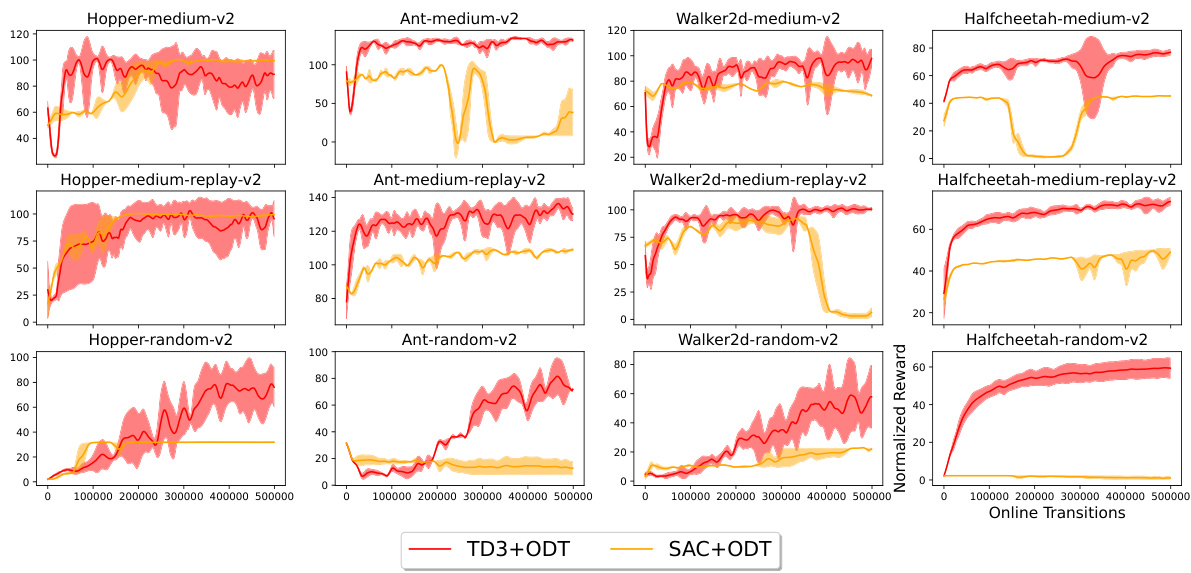
This figure displays the performance of different algorithms on four robotic manipulation tasks from the Adroit environment. Three datasets are used for each task: expert (optimal performance), cloned (imitating expert), and human. The results show that the proposed method (TD3+ODT) significantly outperforms baseline methods like ODT and TD3+BC, particularly when starting from lower-quality cloned or human datasets. While TD3, IQL, and TD3+ODT initially show decent results, the TD3 baseline struggles significantly during online finetuning, highlighting the effectiveness of the proposed approach (TD3+ODT).
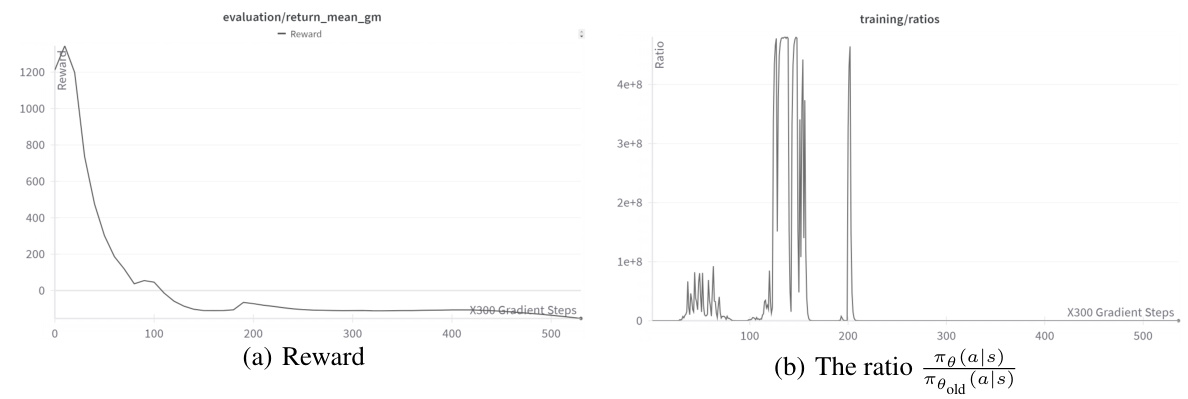
This figure shows the training instability and the performance of a decision transformer finetuned with PPO. The left subplot shows the reward curve, indicating significant instability and poor performance. The right subplot displays the ratio of the current policy to the old policy, again revealing instability. This illustrates the difficulty of using PPO to finetune a decision transformer.

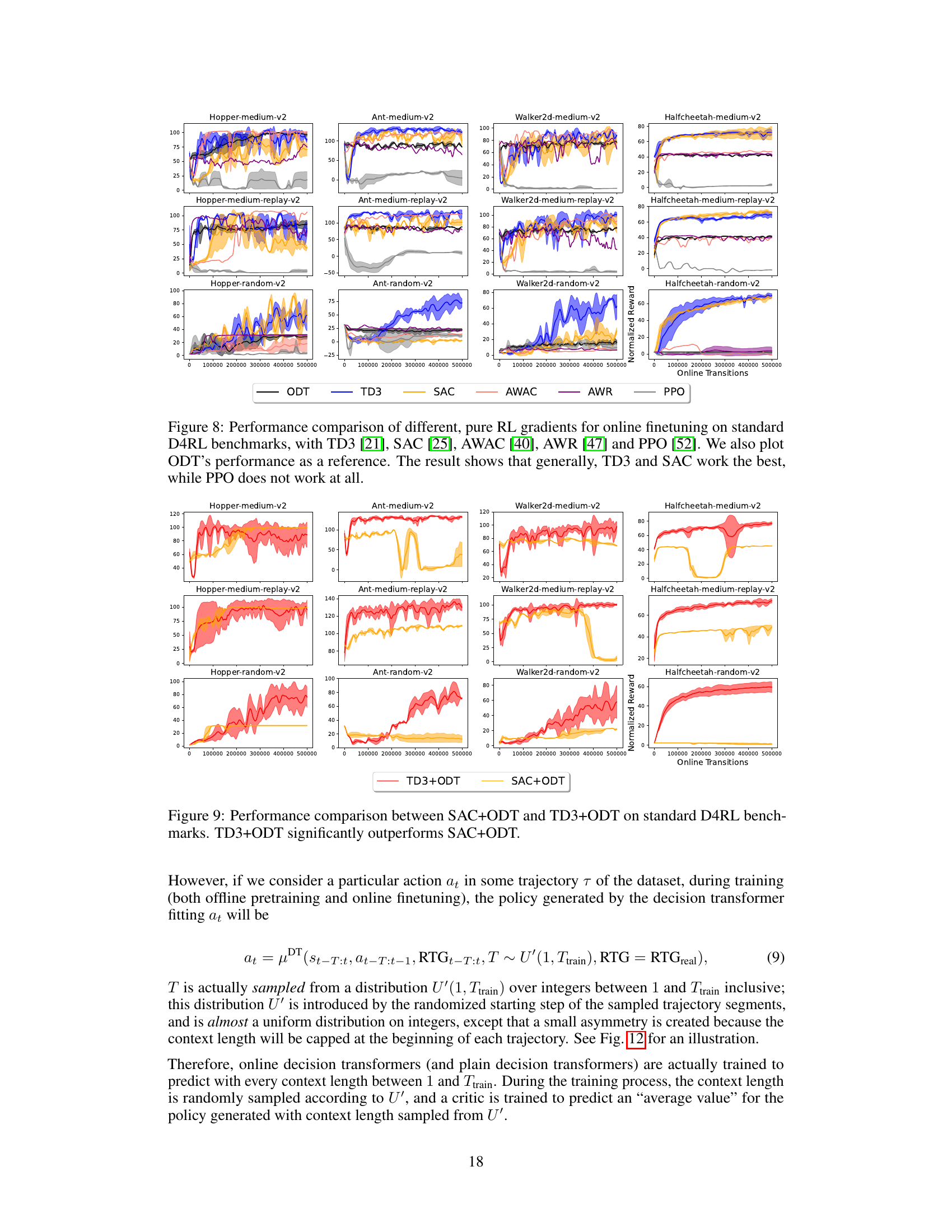
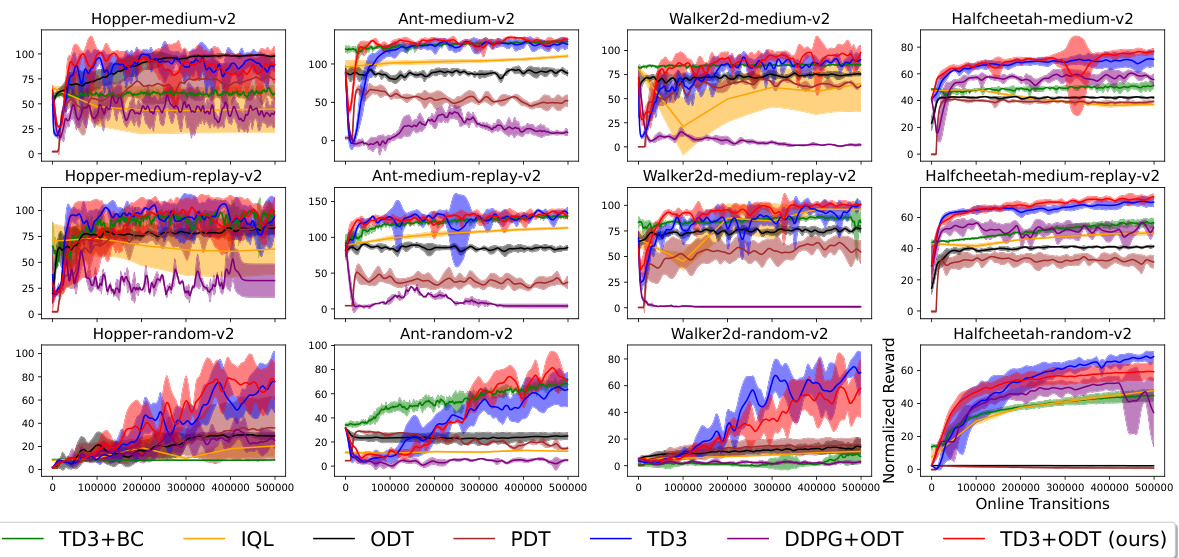
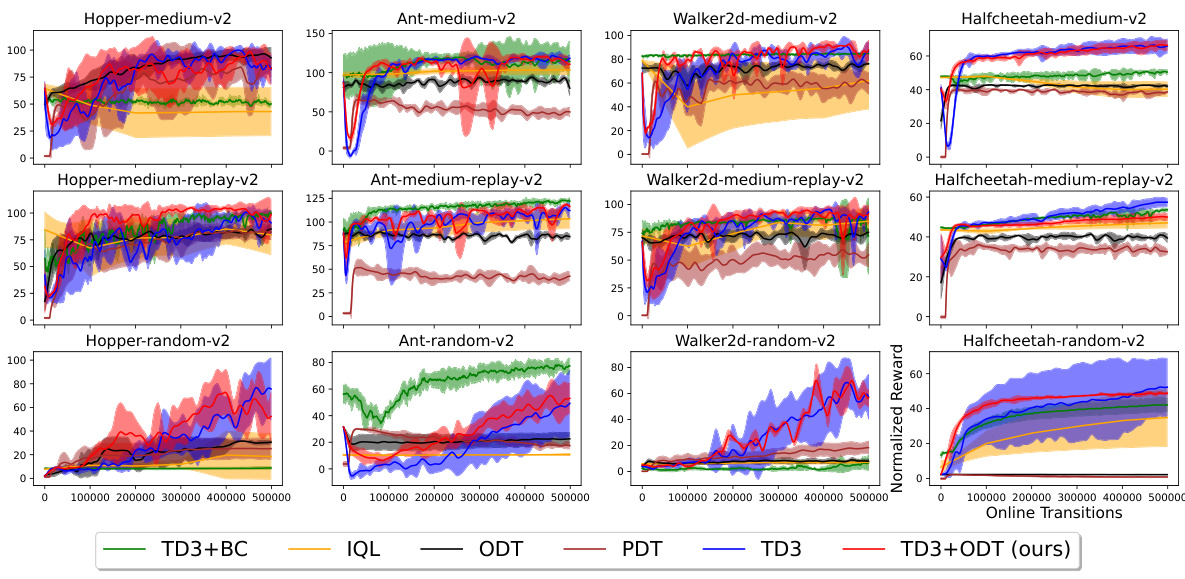
This figure shows the results of the experiments conducted on four MuJoCo environments (Hopper, HalfCheetah, Walker2d, and Ant) using different datasets (medium, medium-replay, and random). The performance of six different methods are compared: TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT (the proposed method). The key observation is that adding TD3 gradients significantly enhances the performance, especially when pretrained with low-reward data. In contrast, autoregressive methods like ODT and PDT struggle, particularly with random datasets, highlighting the benefit of incorporating reinforcement learning gradients in online finetuning of decision transformers.
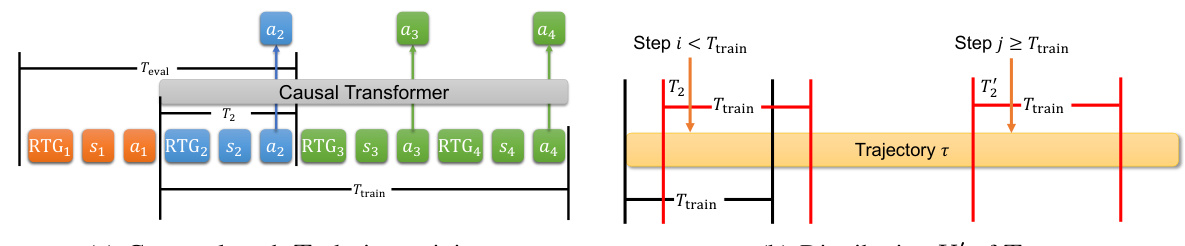
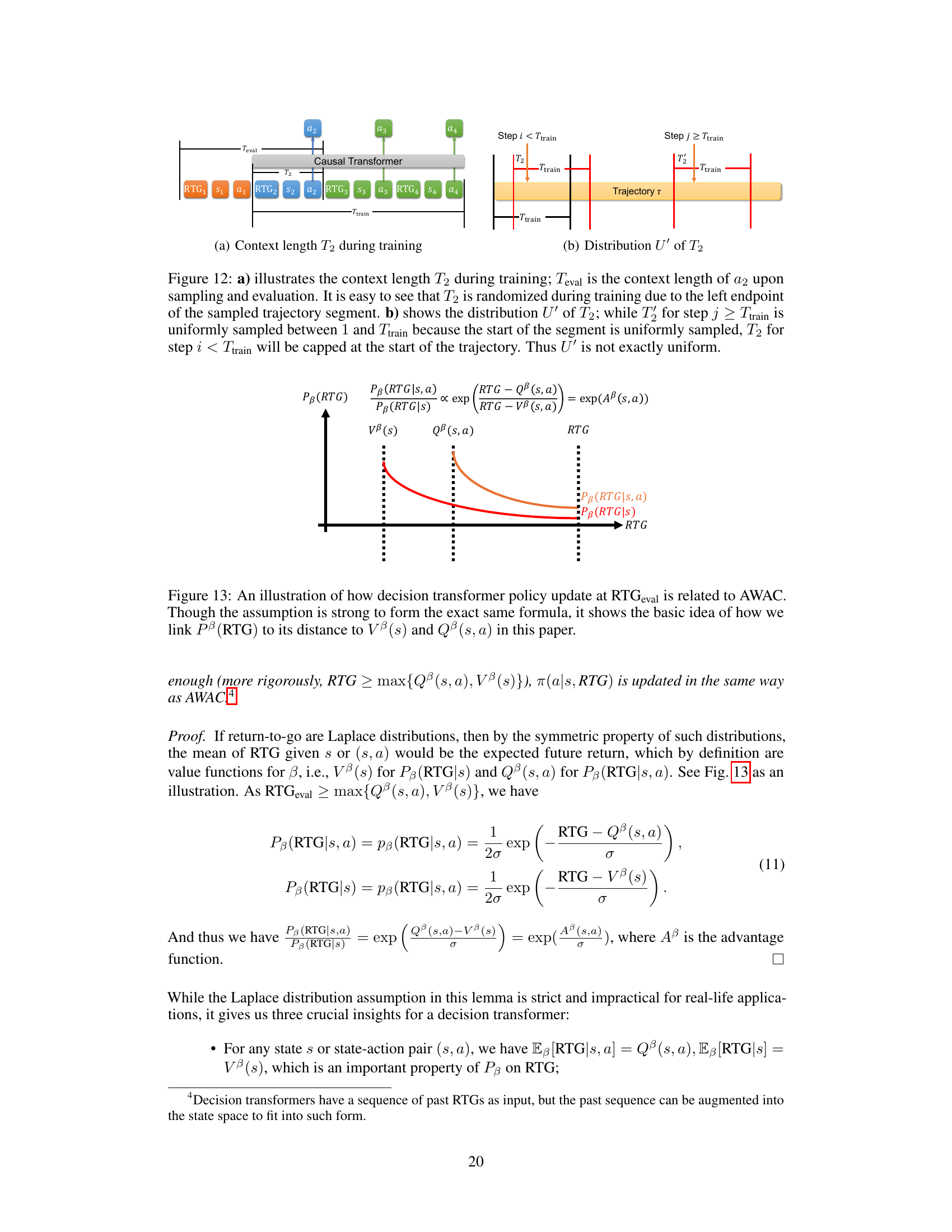
This figure illustrates how the context length used during training and evaluation of the decision transformer model varies. Panel (a) shows the overall architecture, highlighting how the context length (T2) during training differs from the evaluation context length (Teval). Panel (b) focuses on the distribution of context lengths (T2) during training, demonstrating that it is not perfectly uniform due to the way the model samples trajectory segments.
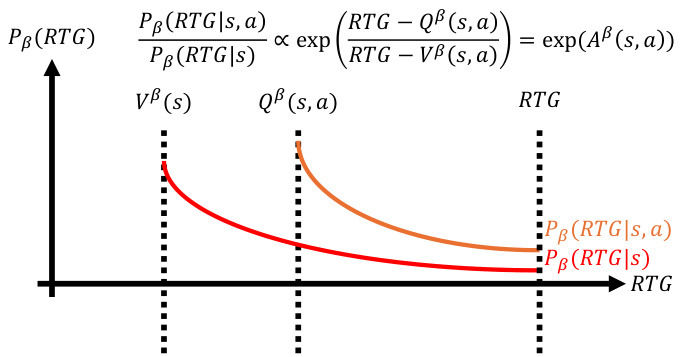
This figure illustrates the limitations of Online Decision Transformers (ODT) when pretrained with low-reward offline data. ODT, using a supervised learning approach, struggles to improve because the gradient it produces (∂RTG/∂a) points in the opposite direction needed for local policy improvement (∂RTG/∂a). The figure shows how the target return-to-go (RTG) is far from the actual return, leading to poor performance. The solution proposed in the paper is to add reinforcement learning (RL) gradients (like those from TD3) to provide the necessary local improvement signal and thus improve the policy.
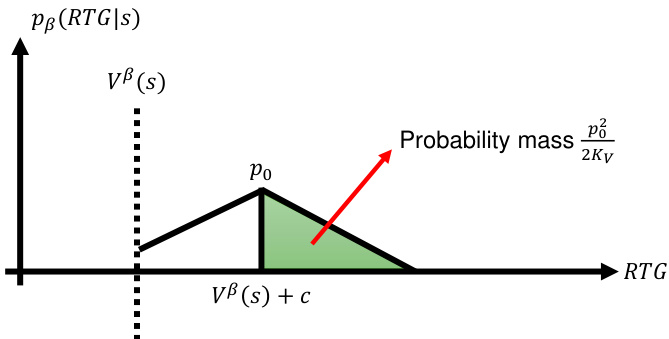
This figure demonstrates the relationship between the probability density function pβ(RTG|s) and the cumulative probability Prβ(RTG > Vβ(s) + c|s) under the assumption that pβ(RTG|s) is Lipschitz continuous. It highlights how the Lipschitz condition, implying a bounded rate of change in the density function, constrains the cumulative probability. The shaded area represents a region of probability mass, and the figure uses this to visually illustrate how a bound on the rate of change in pβ(RTG|s) translates to a bound on the cumulative probability. The exclusion of the left-hand shaded area signifies that the probability mass in that region is not being considered because it could be truncated by Vβ(s).
This figure illustrates the core idea of the paper. Online Decision Transformers (ODT) struggle when pretrained with low-reward data because the gradient of the return-to-go (RTG) with respect to the action, produced by the transformer, points in the opposite direction needed for improvement. Adding reinforcement learning (RL) gradients, such as those from TD3, provides a local improvement signal which addresses this limitation and leads to better online finetuning performance.
This figure illustrates the core idea of the paper. It shows how the Online Decision Transformer (ODT) fails to improve when pretrained with low-reward offline data, highlighting the contrast between the gradient provided by the decision transformer (∂RTG/∂a) and what is needed for local policy improvement (∂RTG/∂a). The figure suggests that by adding RL gradients, the agent can improve locally and achieve better performance. The left panel shows how ODT struggles with an unreachable target RTG (Returns-To-Go), while the right panel illustrates that incorporating TD3 (Twin Delayed Deep Deterministic Policy Gradient) gradients enables local improvement by using a Q-function.
This figure illustrates the core idea of the paper. Online Decision Transformers (ODTs) struggle to improve when pretrained with low-reward data because the gradient they produce (∂RTG/∂a) works against the direction needed for local policy improvement (∂RTG/∂a). Adding RL gradients (such as TD3) allows the agent to improve locally, even if the target RTG is far from the pretrained policy and out of distribution, leading to better overall performance.
This figure shows the performance comparison of different methods on four robotic manipulation tasks from the Adroit environment. The x-axis represents the number of online transitions, and the y-axis represents the normalized average reward. The results demonstrate that the proposed TD3+ODT method outperforms several baselines, including the state-of-the-art Online Decision Transformer (ODT). Notably, while TD3, IQL, and TD3+ODT exhibit decent performance initially, TD3 struggles during online finetuning, whereas TD3+ODT significantly surpasses IQL in terms of performance improvement.
This figure displays the performance comparison of different methods on four Adroit robotic manipulation tasks: Pen, Hammer, Door, and Relocate. Each task is tested with three datasets representing different data quality: expert, cloned, and human. The results demonstrate that adding TD3 gradients to the ODT (Online Decision Transformer) significantly boosts online finetuning performance, particularly when pretrained on low-reward offline data. The figure showcases the average normalized reward curves over 5 different seeds for each method and dataset. Notably, while TD3, IQL, and the proposed TD3+ODT perform well initially, TD3 degrades over time, whereas TD3+ODT consistently outperforms others, highlighting the effectiveness of the proposed approach.
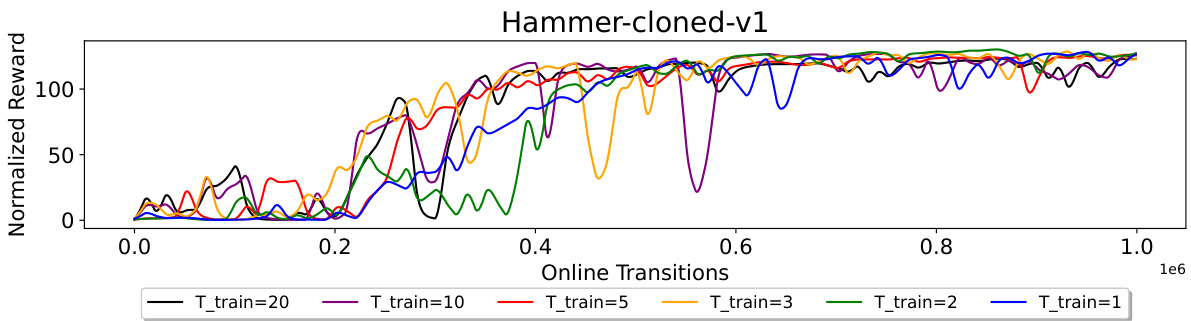
This figure shows the effect of training context length (T_train) on the performance of the online finetuning of a decision transformer on the Hammer-cloned-v1 environment. Different curves represent different values of T_train, showing how the length of the training context affects the learning process. The figure demonstrates that while increasing T_train initially improves the speed of convergence, excessively long context lengths (T_train) lead to instability and fluctuations in the learning process.
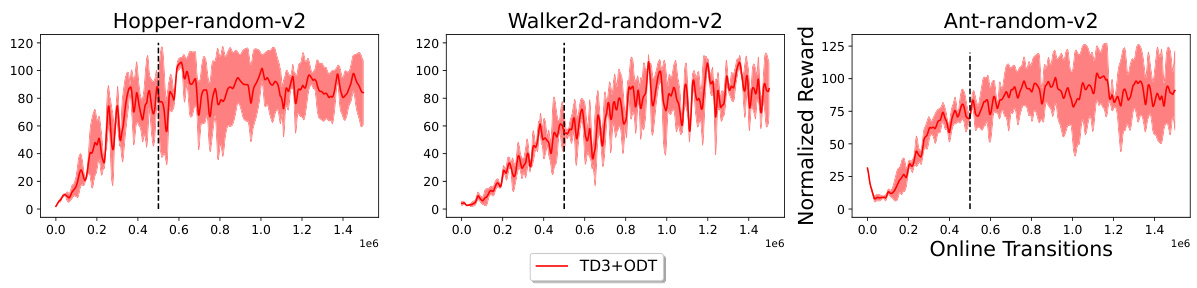
The figure shows the reward curves for three MuJoCo environments (Hopper, Walker2d, and Ant) with random datasets. The x-axis represents the number of online transitions, and the y-axis represents the normalized reward. The red line shows the performance of TD3+ODT, our proposed method. The dashed line indicates the point where the main paper stopped the experiment (500K steps). The figure demonstrates that the TD3+ODT method continues to improve even beyond the 500K step mark, suggesting significant potential for improvement with extended finetuning. The shaded area indicates the standard deviation across 5 random seeds.

This figure demonstrates the limitations of online decision transformers (ODT) when pretrained with low-reward data and how reinforcement learning (RL) gradients can improve performance. It uses a simple MDP with a single state and continuous action space to illustrate how RL algorithms (DDPG, and DDPG combined with ODT) quickly learn to maximize reward and find optimal actions unlike the ODT that struggles. The figure also shows the learned critic function for the RL algorithms correctly approximate the reward function, while the ODT policy fails to identify a high-reward region, showcasing the benefit of incorporating RL gradients for online finetuning.
This figure shows ablation studies on the effect of different training context lengths (T_train) on the performance of the TD3+ODT algorithm in the Hammer-cloned-v1 environment. The results reveal that a longer training context length (T_train) leads to faster convergence during the initial phase of online finetuning. However, excessively long T_train values result in training instability and performance fluctuations. The optimal T_train value appears to be a balance between capturing sufficient context for accurate decision-making and preventing instability. The shaded regions illustrate confidence intervals across multiple experimental runs.
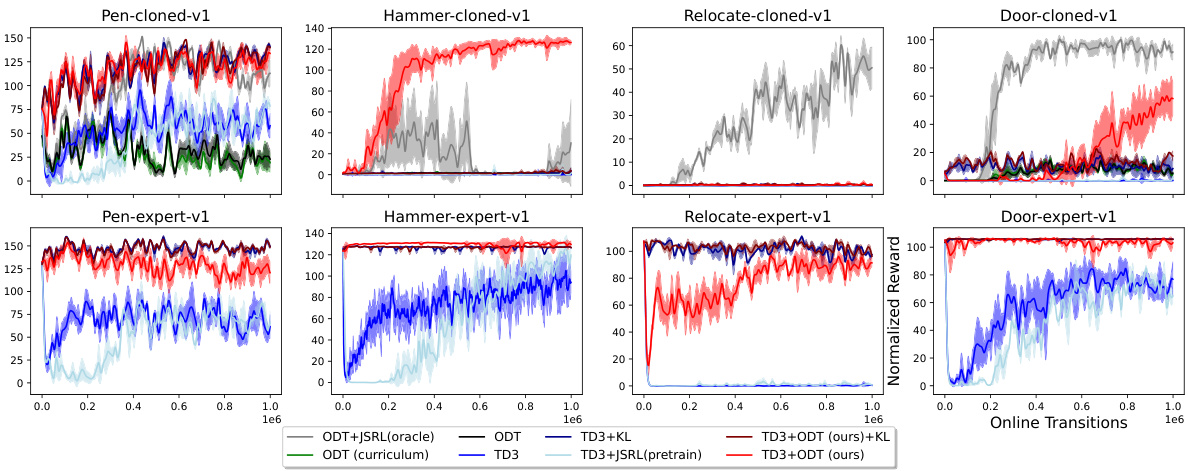
This figure compares the performance of different methods for online finetuning on the Adroit robotic manipulation tasks. It shows the normalized average reward over online transitions for several methods, including the proposed TD3+ODT, as well as baselines like ODT, PDT, TD3, TD3+BC, IQL, and DDPG+ODT. The results demonstrate that TD3+ODT significantly outperforms the baselines, especially in scenarios where the offline data has low rewards. While some other methods perform decently at the start of online finetuning, TD3+ODT shows considerably better improvement over time.
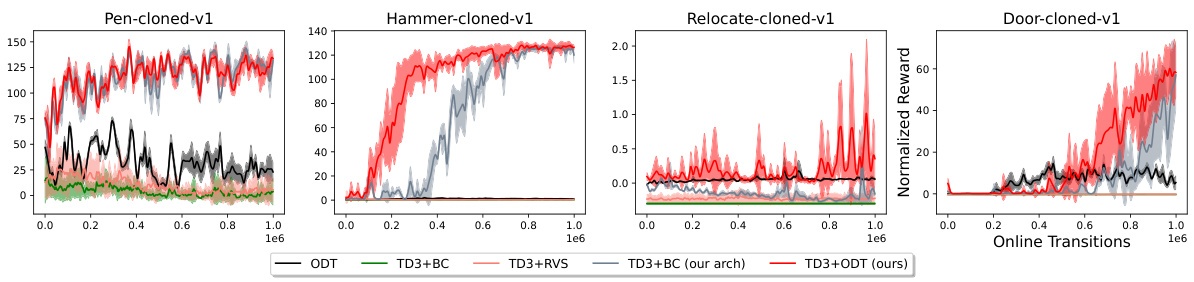
This figure presents an ablation study comparing several methods for online finetuning of decision transformers on the Adroit environment. The goal is to determine the impact of different components on performance. The methods compared include the original Online Decision Transformer (ODT), TD3+BC (a baseline combining TD3 and behavior cloning), TD3+RVS (using a supervised learning approach similar to the original Decision Transformer), TD3+BC with the transformer architecture from the proposed method (TD3+ODT), and the complete proposed method (TD3+ODT). The results demonstrate that only using the proposed method’s architecture with TD3+BC leads to improved performance, although still below the full method.
This figure presents ablation studies to isolate the impact of the transformer architecture and the RL-via-supervised-learning (RvS) method on the overall performance. Four methods were compared: ODT (baseline), TD3+BC, TD3+RvS (both using the original TD3+BC architecture), and TD3+BC using the transformer architecture from the proposed method. The results across four Adroit environments highlight that only the combination of TD3+BC with the transformer architecture shows some improvement, demonstrating the importance of the chosen architecture in achieving better performance than the baseline ODT. However, even this modified TD3+BC architecture did not achieve the same results as the proposed method (TD3+ODT), further emphasizing the synergistic effect of combining both the RL gradient and the transformer.
More on tables
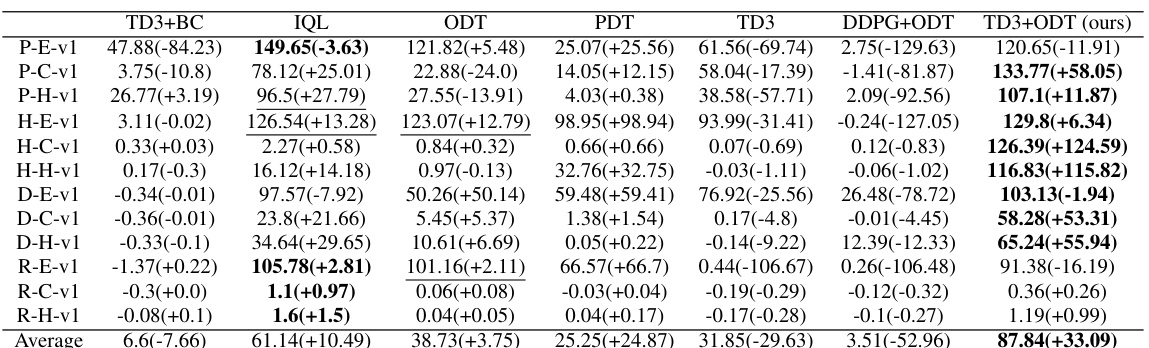
This table presents the average reward achieved by different methods (TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT) on four Adroit manipulation tasks (Pen, Hammer, Door, Relocate) before and after online finetuning. Three different datasets are used for each task: expert, cloned, and human. The best-performing method for each setting is highlighted, and any result within 90% of the best performance is underlined. The table demonstrates the significant improvement achieved by the proposed TD3+ODT method over other approaches, especially in addressing the training instability issues encountered with DDPG.
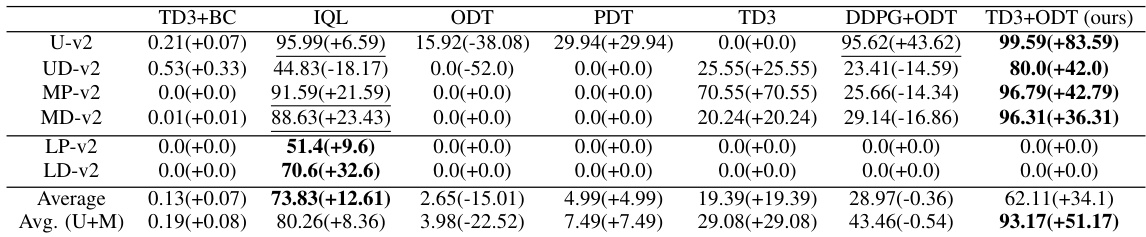
This table presents the average reward achieved by different methods (TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT) on various Antmaze environments (Umaze, Umaze-Diverse, Medium-Play, Medium-Diverse, Large-Play, and Large-Diverse) before and after online finetuning. The results are summarized for each environment and dataset, indicating the final average reward and the increase achieved after finetuning. The best-performing method for each environment and dataset is highlighted.
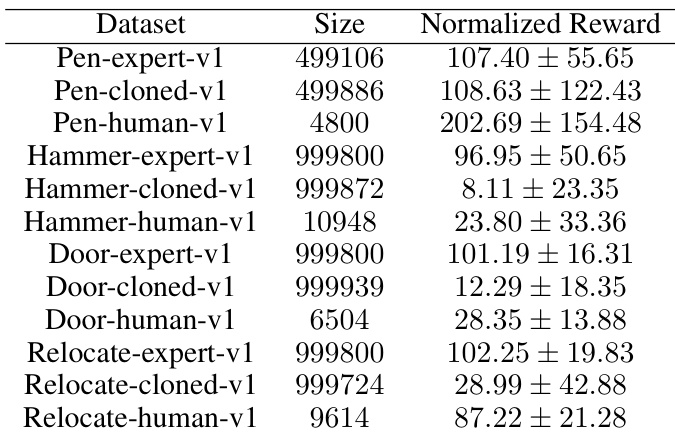
This table shows the size and the average and standard deviation of the normalized reward of the Adroit datasets used in the experiments. The Adroit dataset contains four robotic manipulation tasks (Pen, Hammer, Door, Relocate) and three different data qualities (expert, cloned, human) for each task. The size column represents the number of transitions in each dataset. The normalized reward represents the average performance achieved on that specific task/dataset by an agent.
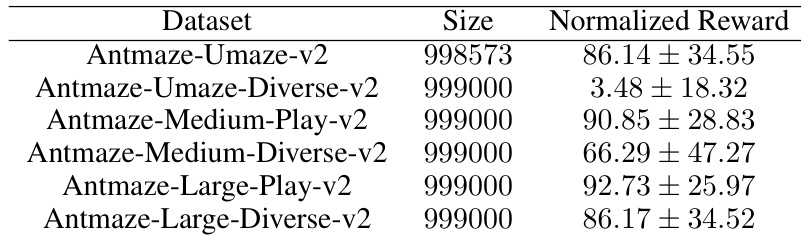
This table presents the dataset size and the average normalized reward (along with standard deviation) for six different Antmaze environments from the D4RL benchmark. These environments vary in terms of maze size and the diversity of starting positions and goals. The data is used in the paper’s experiments to evaluate the performance of different reinforcement learning algorithms. The table allows for a comparison of performance across environments with different levels of complexity.
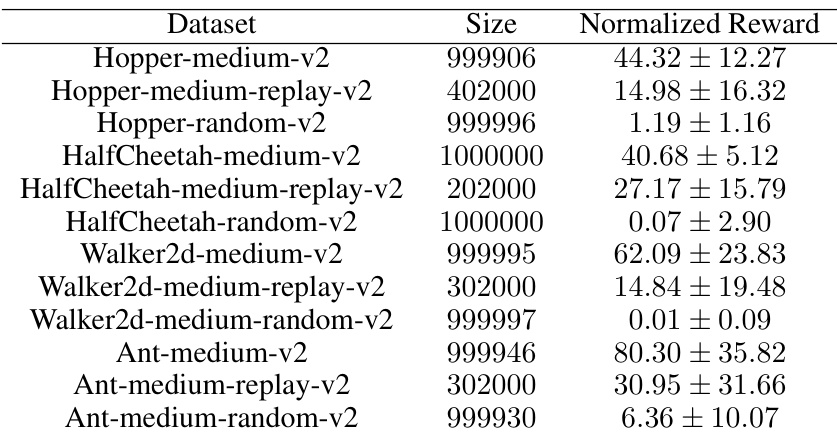
This table presents the characteristics of the MuJoCo datasets used in the experiments. For each environment (Hopper, HalfCheetah, Walker2d, Ant), three datasets are provided: medium, medium-replay, and random. The ‘Size’ column indicates the number of data points in each dataset. The ‘Normalized Reward’ column shows the average normalized reward and its standard deviation, indicating the performance level of the data within each dataset. This information is crucial for understanding the context and performance baselines of the experiments involving MuJoCo environments.
This table presents the average reward achieved by different methods before and after online finetuning on Adroit environments (Pen, Hammer, Door, Relocate). Three different datasets are used: expert, cloned, and human. The table highlights the best-performing method for each setting and underlines results within 90% of the best performance. The caption notes that our proposed method (TD3+ODT) significantly outperforms the baselines, especially considering DDPG+ODT’s instability.
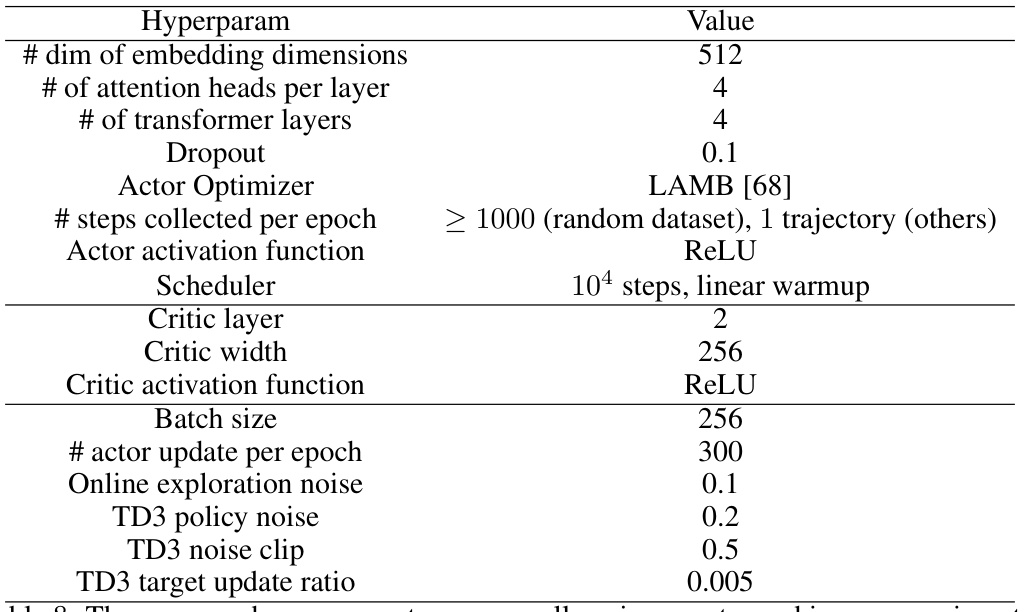
This table lists the hyperparameters used across different reinforcement learning environments in the experiments. These parameters are consistent across all the environments and include details about the embedding dimensions, attention heads, transformer layers, dropout rate, actor optimizer, number of steps collected per epoch, actor activation function, scheduler details, critic layers, critic width, critic activation function, batch size, actor updates per epoch, online exploration noise, TD3 policy noise, TD3 noise clip, and the TD3 target update ratio. These settings were common to ensure fair comparison across the experiments.
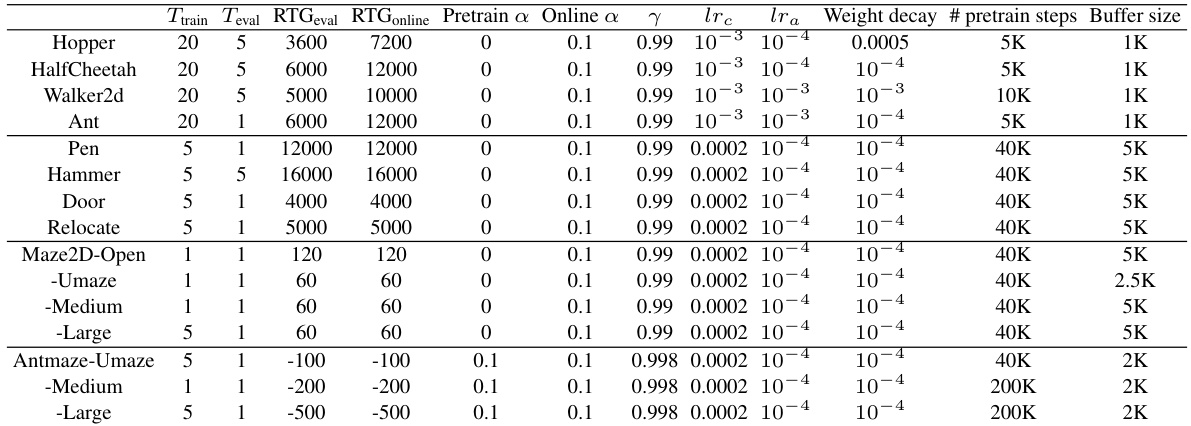
This table lists the hyperparameters used in the experiments of the paper, specifically those that vary depending on the environment used. It provides details such as the training and evaluation context lengths (Ttrain and Teval), the target return-to-go values during evaluation and online rollout (RTGeval and RTGonline), the coefficient for RL gradients (a), the discount factor (γ), the critic and actor learning rates (lrc and lra), weight decay, the number of pretraining steps, and the buffer size. The table also notes that the return-to-go values for the Antmaze environment were adjusted due to reward shaping.
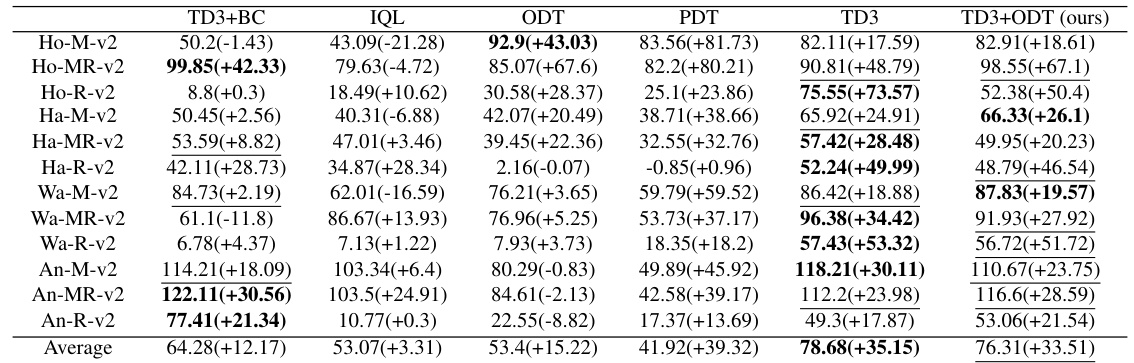
This table presents the average reward achieved by different methods (TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT) on MuJoCo environments before and after online finetuning. The environments tested are Hopper, HalfCheetah, Walker2d, and Ant, each with Medium, Medium-Replay, and Random datasets. The best performing method for each environment is bolded, and results within 90% of the best are underlined. The table shows the final average reward and the improvement gained after online finetuning. The ‘final’ column indicates the average reward after online finetuning, and the value in parentheses represents the increase in reward compared to the pre-finetuning performance. This table highlights the superior performance of the proposed TD3+ODT method in several of the scenarios.

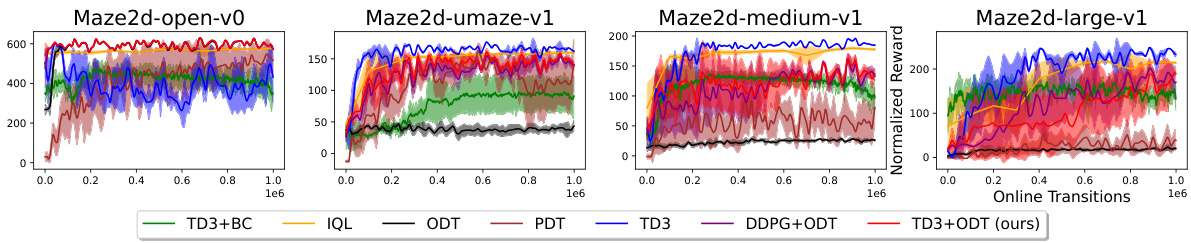
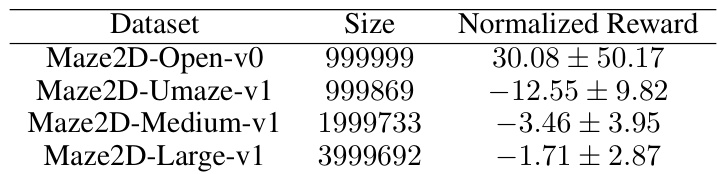
This table presents the average reward achieved by different offline-to-online reinforcement learning methods on four variants of the Maze2D environment before and after online finetuning. The methods compared include TD3+BC, IQL, ODT, PDT, TD3, DDPG+ODT, and TD3+ODT (the proposed method). The results show the average reward achieved by each method before and after online fine-tuning, illustrating the improvement achieved by each method after the online finetuning process. The table highlights that the TD3+ODT method, while performing slightly worse than IQL, substantially outperforms the other methods.
Full paper#