↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Reinforcement learning (RL) struggles with delayed observations, commonly addressed by state augmentation. However, this leads to increased state space dimensionality, hindering learning efficiency. Existing solutions using Temporal Difference (TD) learning still face this challenge.
Variational Delayed Policy Optimization (VDPO) offers a novel approach by framing delayed RL as a variational inference problem. It tackles the issue through a two-step iterative process: first, TD learning on a delay-free smaller state space environment to create a reference policy. Second, behaviour cloning efficiently imitates this policy in the delayed environment. VDPO demonstrates superior sample efficiency (approximately 50% less samples) compared to state-of-the-art methods in MuJoCo benchmark tasks without compromising performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reinforcement learning (RL) in environments with delayed observations. It introduces a novel framework, VDPO, that significantly improves sample efficiency without sacrificing performance, a critical challenge in this domain. This work opens new avenues for applying RL to real-world scenarios where delays are prevalent, such as robotics and control systems.
Visual Insights#
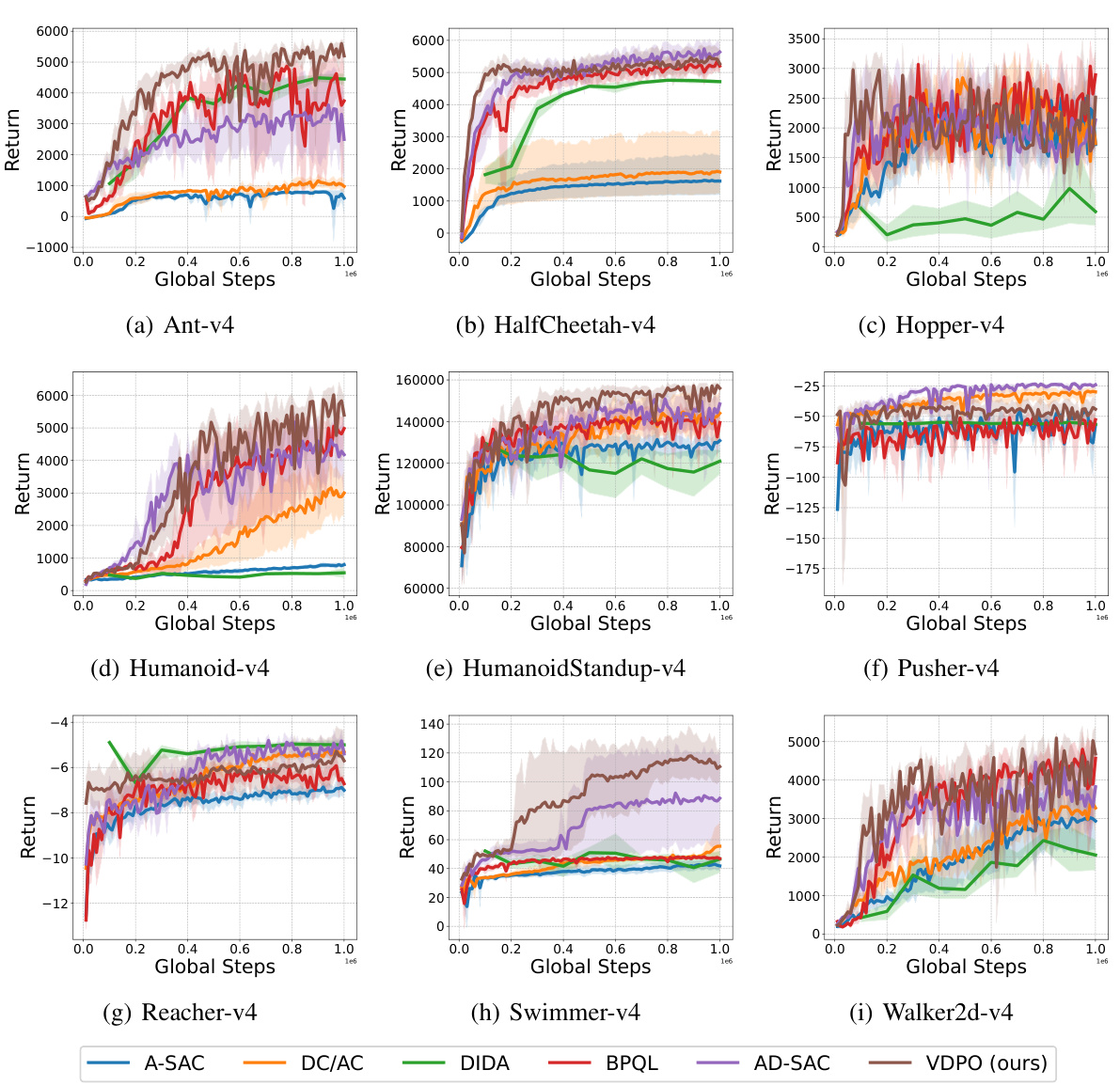
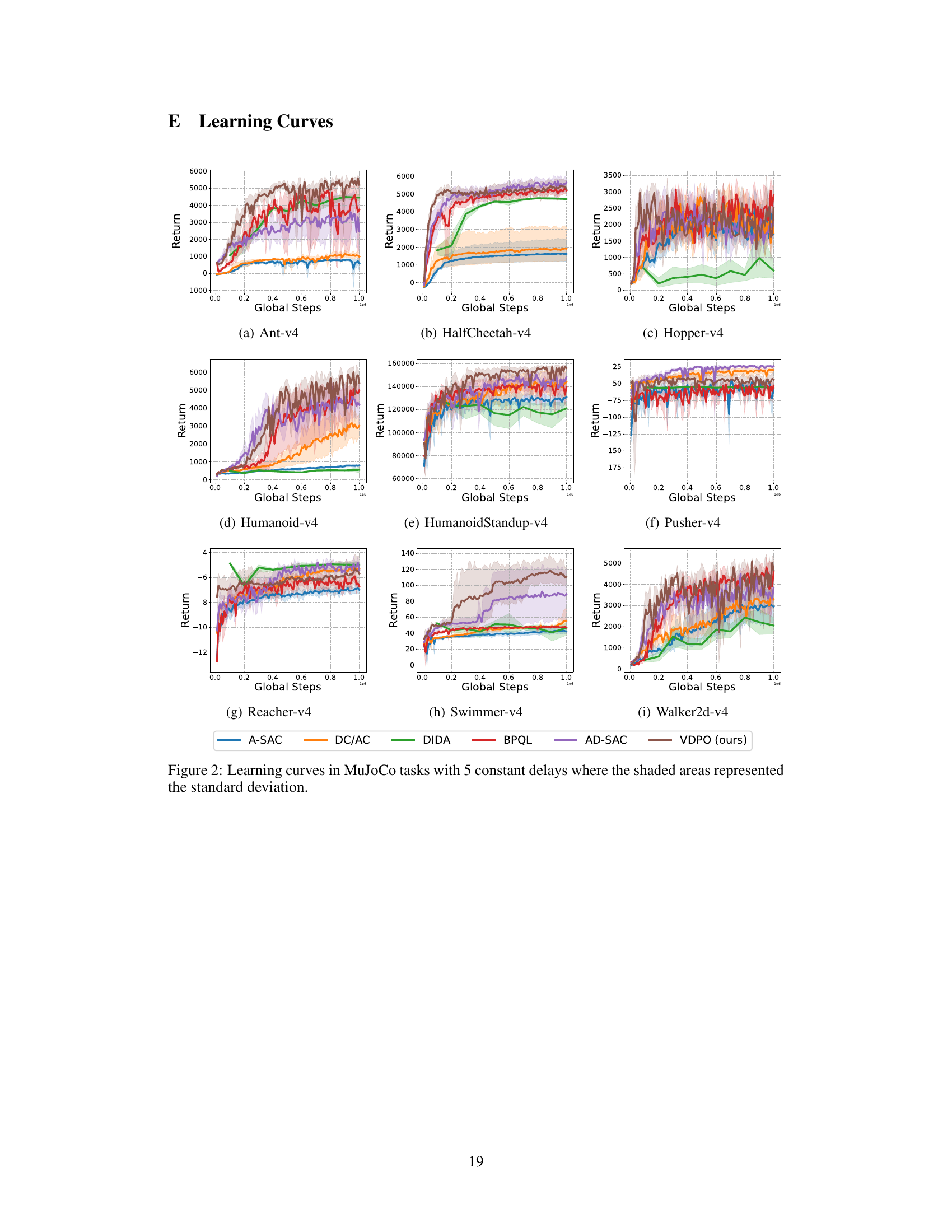
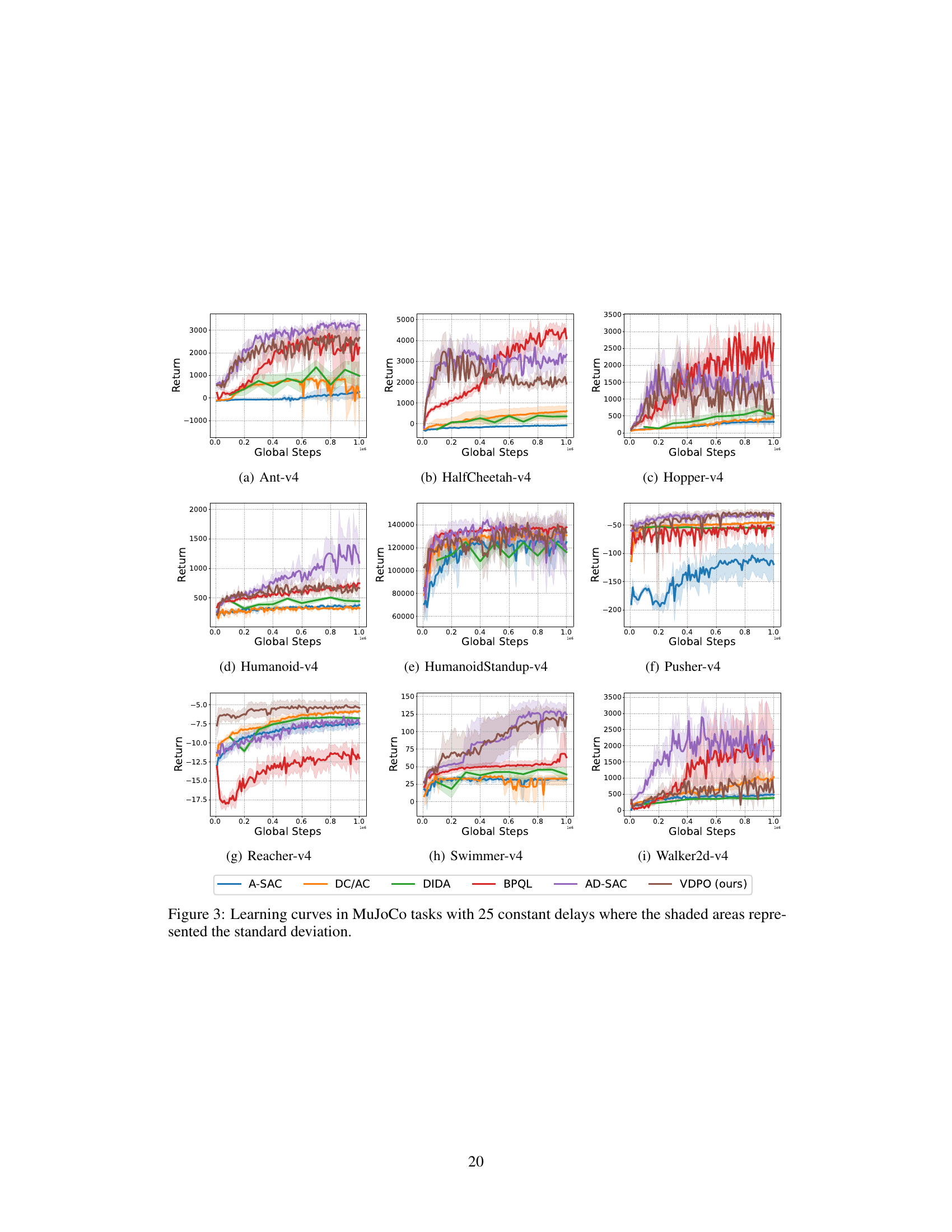
This figure shows the learning curves for different reinforcement learning algorithms on various MuJoCo tasks with a constant delay of 5 time steps. The y-axis represents the return, and the x-axis shows the global steps. The shaded regions indicate the standard deviation across multiple runs, providing a measure of the variability in the algorithm’s performance. The plot allows for a comparison of the learning efficiency and stability of different algorithms (A-SAC, DC/AC, DIDA, BPQL, AD-SAC, and VDPO) under the challenging condition of delayed observations.
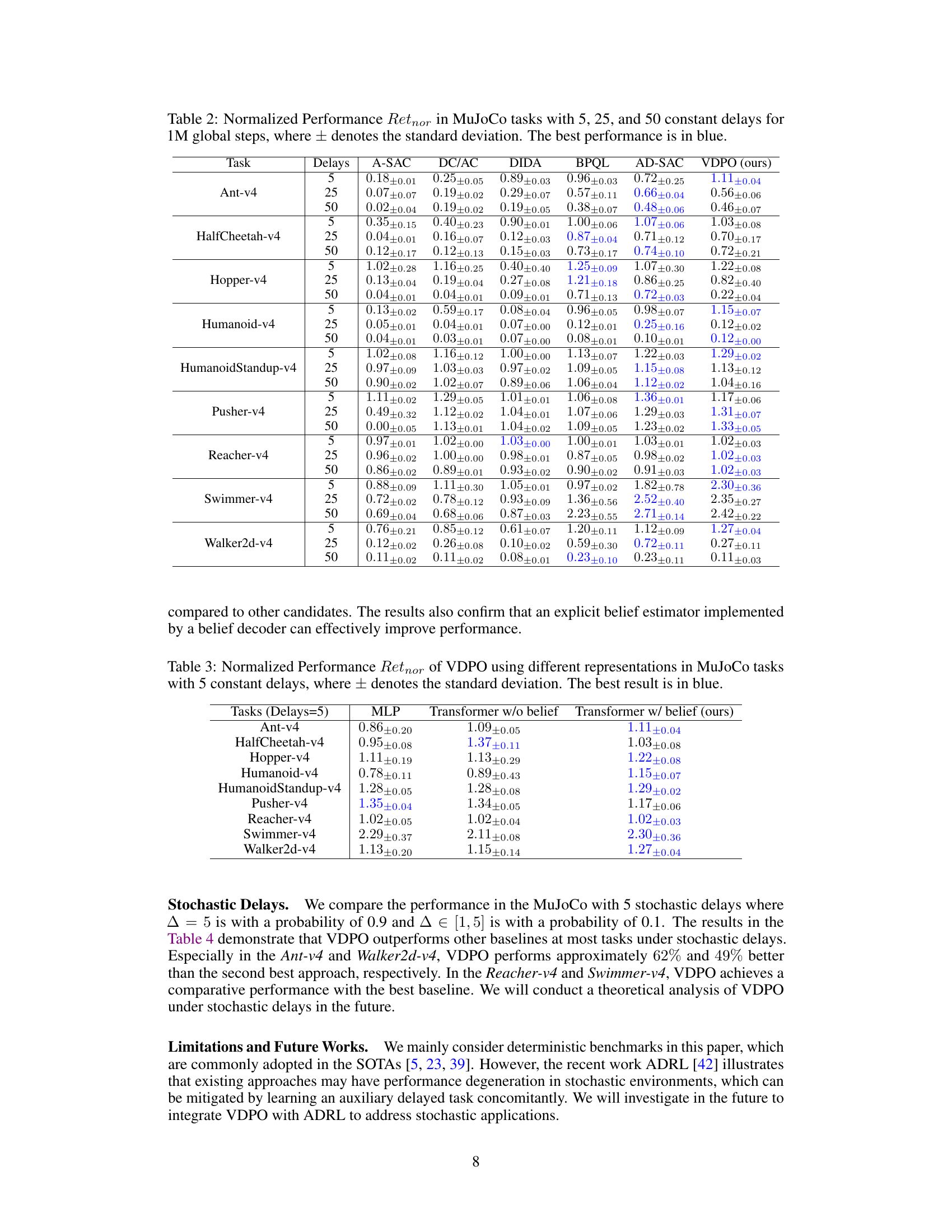
This table presents the sample efficiency results of VDPO and several baseline algorithms on nine MuJoCo tasks with a constant delay of 5. The goal is to reach a performance threshold (Retaf), defined by the performance of a delay-free policy trained using SAC. The table shows the number of steps required by each algorithm to reach this threshold within a maximum of 1 million global steps. ‘×’ indicates that the algorithm failed to reach the threshold within the time limit. The best result for each task is highlighted in blue, demonstrating VDPO’s superior sample efficiency.
In-depth insights#
Delayed RL Problem#
The core challenge in delayed reinforcement learning (RL) stems from the broken Markovian property induced by the delay. Standard RL algorithms assume that the current state encapsulates all necessary information for optimal decision-making. However, when observations are delayed, the agent lacks access to the most recent states, leading to significant learning difficulties. This necessitates innovative solutions to either restore the Markovian property or develop algorithms robust to non-Markovian dynamics. State augmentation, a common approach, involves adding past actions and observations to the state, effectively creating a larger, more complex state space. However, this approach also suffers from increased computational cost and sample complexity. Variational methods offer a promising alternative by casting delayed RL as a variational inference problem, which enables the use of optimization tools that may be less sensitive to the high-dimensionality problem of state augmentation. Ultimately, effective solutions require careful consideration of the trade-off between performance and computational efficiency, and exploring new theoretical frameworks remains an active area of research.
Variational Approach#
A variational approach to delayed reinforcement learning offers a powerful alternative to traditional methods. By framing the problem as variational inference, it elegantly addresses the challenge of sample inefficiency inherent in delayed MDPs. The core idea is to decouple the learning process into two steps: First, a reference policy is learned in a delay-free environment, simplifying the state space and making learning efficient. Second, behavior cloning efficiently adapts this policy to the delayed setting. This two-step approach leverages the strengths of both TD learning and imitation learning, achieving significant sample efficiency gains while maintaining strong performance. The theoretical analysis further supports the method’s effectiveness, demonstrating reduced sample complexity compared to TD-only approaches. However, limitations exist, particularly in handling stochastic delays, which suggests further investigation is needed. Overall, the variational approach represents a significant advancement in addressing the complexities of delayed reinforcement learning.
Sample Efficiency#
The concept of sample efficiency in reinforcement learning (RL) is crucial, especially when dealing with complex environments. Reducing the number of samples needed to achieve a desired performance level translates directly to reduced training time and computational costs. The paper focuses on improving sample efficiency in delayed reinforcement learning scenarios, which are inherently more challenging due to the non-Markovian nature of the problem. The authors introduce a novel framework, VDPO, that leverages variational inference to reformulate the problem, leading to a significant enhancement in sample efficiency compared to state-of-the-art techniques. This is achieved by using a two-step optimization approach: TD learning in a simplified delay-free environment, followed by behaviour cloning in the delayed setting. The theoretical analysis and empirical results demonstrate a substantial improvement, achieving comparable performance with approximately 50% fewer samples. This highlights the effectiveness of the proposed method in addressing the sample complexity challenges frequently encountered in delayed RL. However, the analysis is limited to specific benchmarks and delay settings, raising questions about its generalizability. Future work should focus on broader evaluations and extensions to stochastic delay scenarios to fully validate the robustness and practical applicability of VDPO.
VDPO Algorithm#
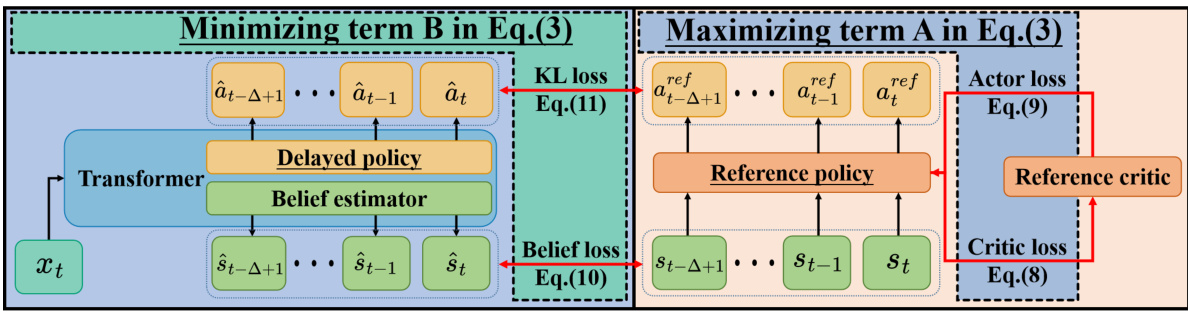
The Variational Delayed Policy Optimization (VDPO) algorithm presents a novel approach to address the challenges of reinforcement learning in environments with delayed observations. VDPO cleverly reframes the delayed RL problem as a variational inference task, thereby leveraging the power of variational methods for efficient optimization. This reformulation leads to a two-step iterative process: first, a reference policy is learned in a delay-free environment using traditional TD learning methods, capitalizing on the smaller state space for enhanced efficiency. Second, behavior cloning is employed to adapt this reference policy to the delayed setting, significantly reducing the computational burden typically associated with TD learning in high-dimensional augmented state spaces. The theoretical analysis supports VDPO’s enhanced sample efficiency by demonstrating that it achieves comparable performance to state-of-the-art methods while requiring substantially fewer samples. The empirical results further validate this claim, showcasing significant improvements in sample efficiency across various MuJoCo benchmark tasks. The algorithm’s inherent flexibility in choosing the delay-free RL method adds another layer of appeal, allowing researchers to tailor the approach to specific problem needs.
Future Works#
The paper’s discussion of future work highlights several promising avenues. Extending the VDPO framework to handle stochastic delays is crucial for real-world applicability, as constant delays are rarely encountered in practice. This requires a more robust theoretical analysis and potentially algorithmic modifications to the core VDPO approach. Investigating different neural network architectures beyond the transformer-based approach used in this study could further enhance sample efficiency and overall performance. Comparing VDPO’s performance against a broader set of baselines, particularly those designed for stochastic delays, would strengthen the conclusions. Finally, exploring applications in more complex, high-dimensional environments would demonstrate the scalability and generalizability of VDPO and its ability to handle more realistic scenarios.
More visual insights#
More on figures
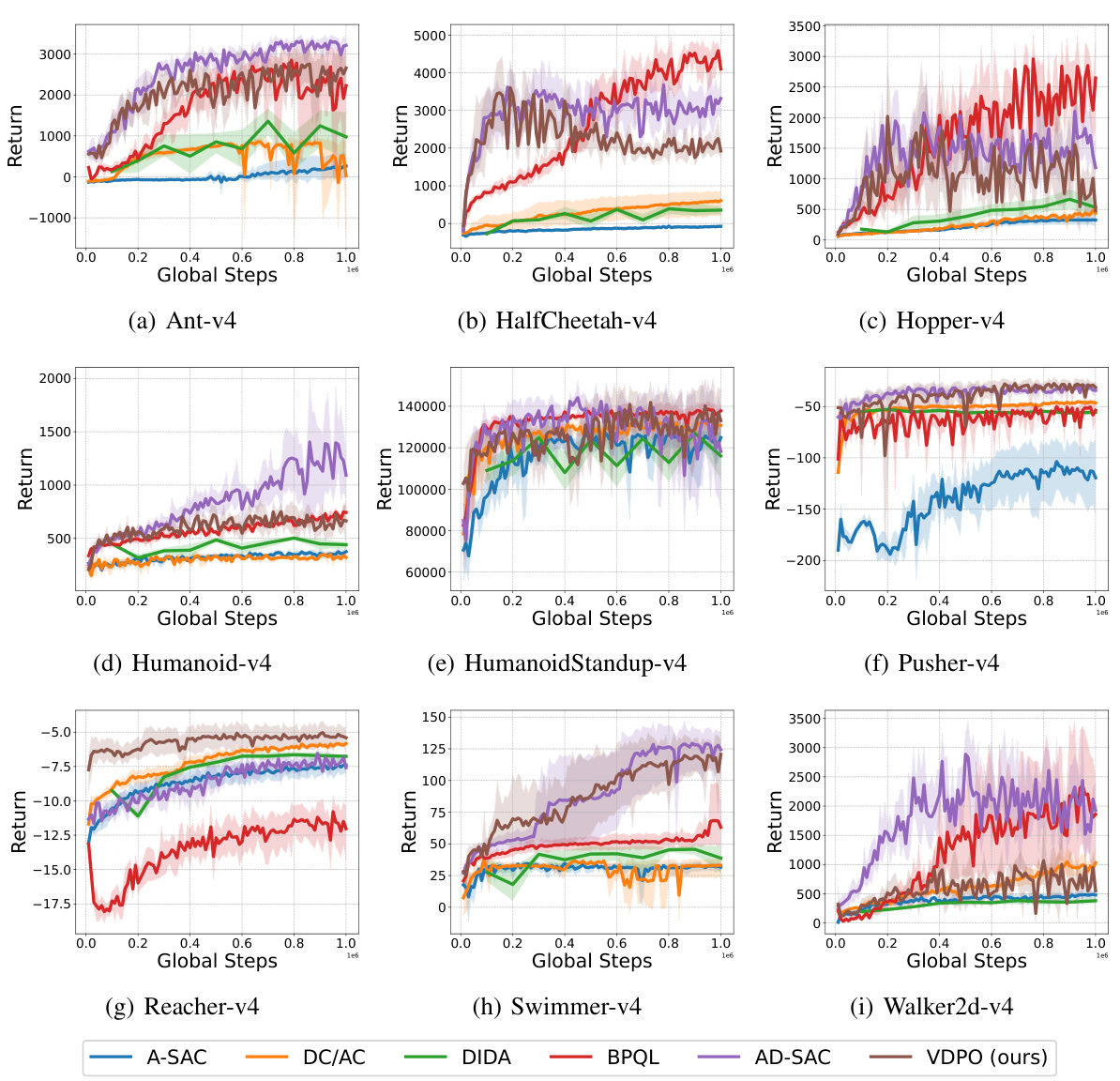
This figure displays the learning curves for various reinforcement learning algorithms across different MuJoCo tasks with a constant delay of 5 steps. The x-axis represents the number of global steps, while the y-axis shows the return. Shaded regions indicate the standard deviation across multiple runs, providing insight into the stability and performance variability of each algorithm. The figure allows for comparison of the learning efficiency and performance of different algorithms under delayed reward scenarios.
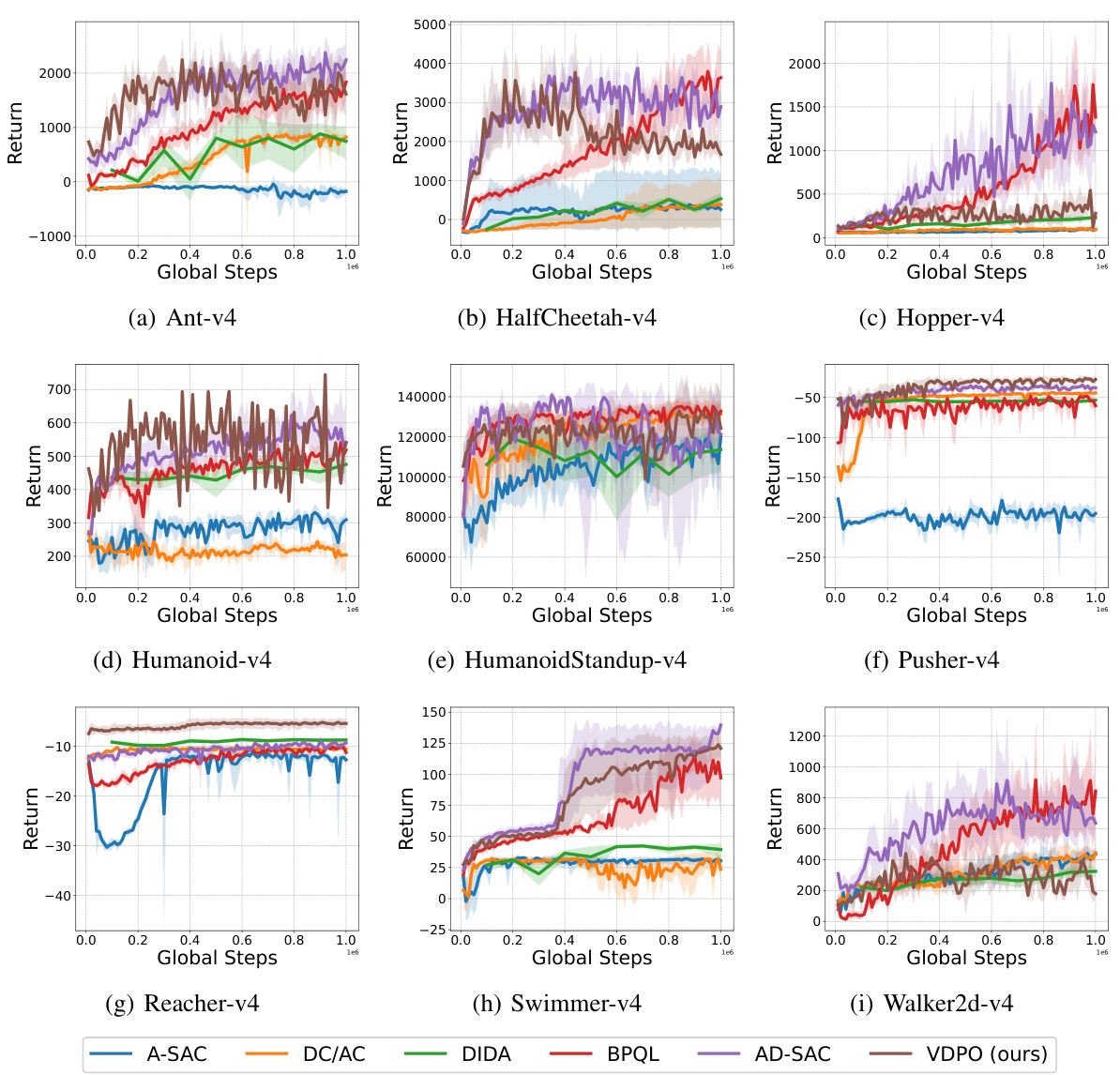
This figure shows the learning curves for different reinforcement learning algorithms on various MuJoCo benchmark tasks with a constant observation delay of 5 timesteps. The algorithms compared include A-SAC, DC/AC, DIDA, BPQL, AD-SAC, and the proposed VDPO. The y-axis represents the average return, and the x-axis represents the number of global steps. Shaded areas indicate the standard deviation across multiple runs, demonstrating the performance consistency and stability of each algorithm. The figure illustrates the relative performance of each algorithm in terms of convergence speed and final performance.
More on tables

This table presents the sample efficiency results for nine different MuJoCo benchmark tasks, each with a constant delay of 5. It shows the number of steps required by various algorithms (A-SAC, DC/AC, DIDA, BPQL, AD-SAC, and VDPO) to reach a performance threshold (Retaf) set by a delay-free SAC policy within a maximum of 1 million global steps. ‘X’ indicates that an algorithm failed to reach the threshold within the limit. The best-performing algorithm for each task is highlighted in blue, showcasing VDPO’s superior sample efficiency.
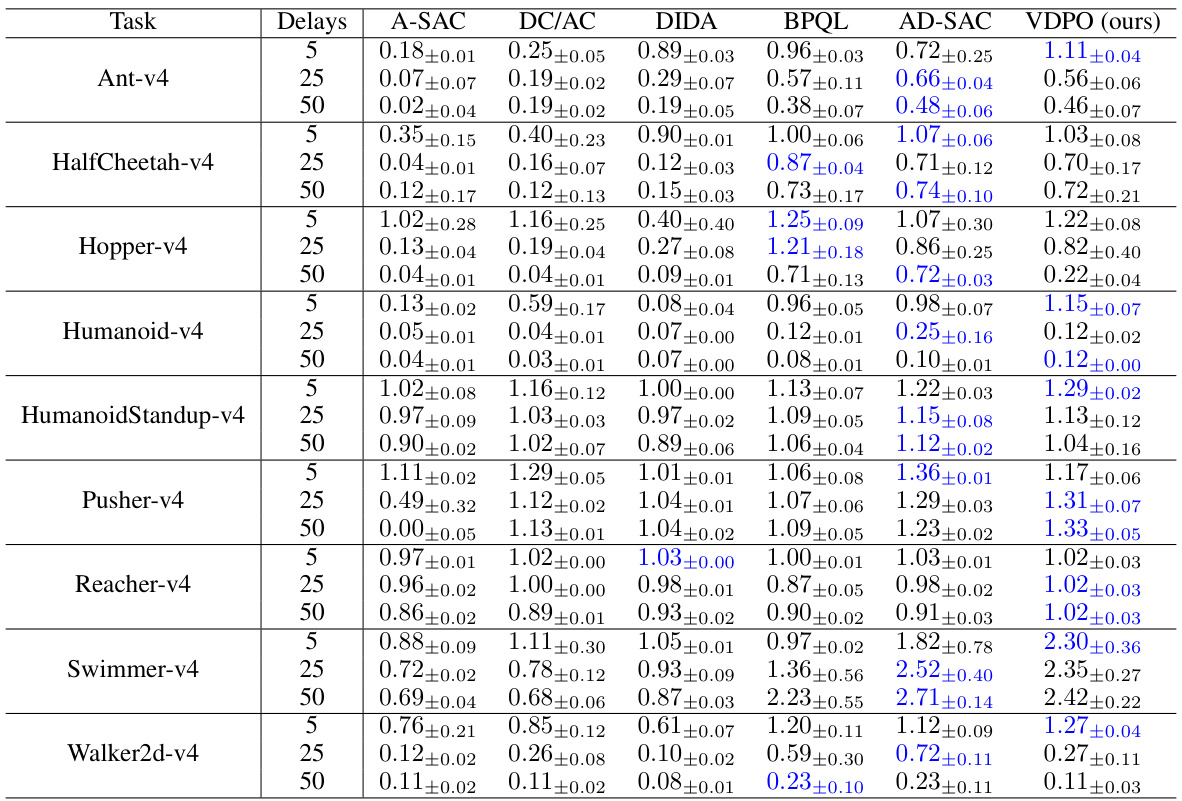
This table presents the normalized performance (Retnor) of different reinforcement learning algorithms on various MuJoCo tasks with varying constant delays (5, 25, and 50). The best-performing algorithm for each task and delay setting is highlighted in blue. The table allows for a comparison of algorithm performance across different delay conditions and highlights the relative strengths of the algorithms in handling observation delays.
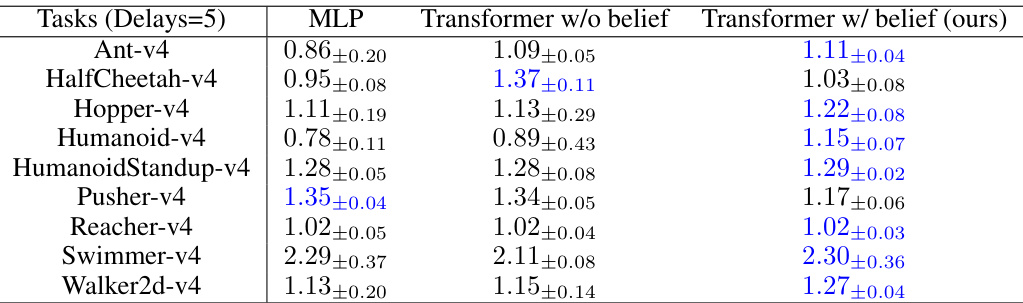
This table presents the results of an ablation study on the different neural network representations used in the VDPO algorithm. It compares the performance (normalized performance indicator) across nine MuJoCo benchmark tasks using three different architectures: a Multilayer Perceptron (MLP), a Transformer without a belief decoder, and the proposed Transformer with a belief decoder. The best performing architecture for each task is highlighted in blue, indicating the superiority of the proposed Transformer with a belief decoder in terms of sample efficiency and overall performance.
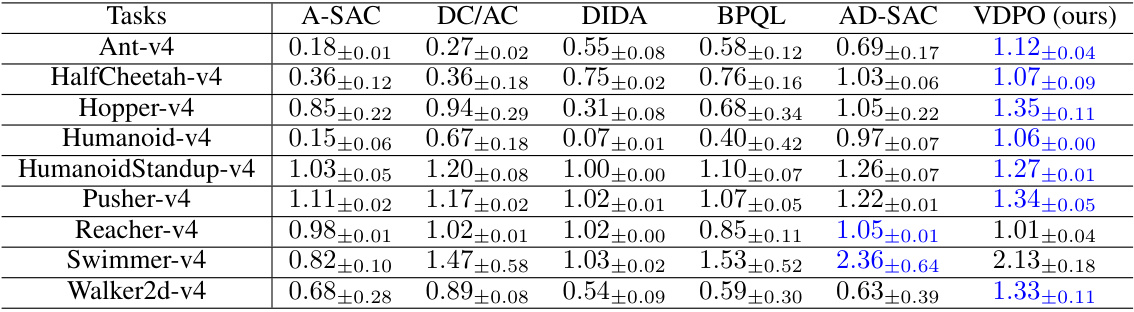
This table presents the performance comparison of VDPO and other state-of-the-art methods across multiple MuJoCo benchmark tasks. The performance is normalized using the formula Retnor = Retalg - Retrand, where Retalg and Retrand represent the algorithm’s performance and random policy performance, respectively. Results are shown for 5, 25, and 50 constant delays, with the best performance in each scenario highlighted in blue. The ± values indicate the standard deviation across multiple runs.
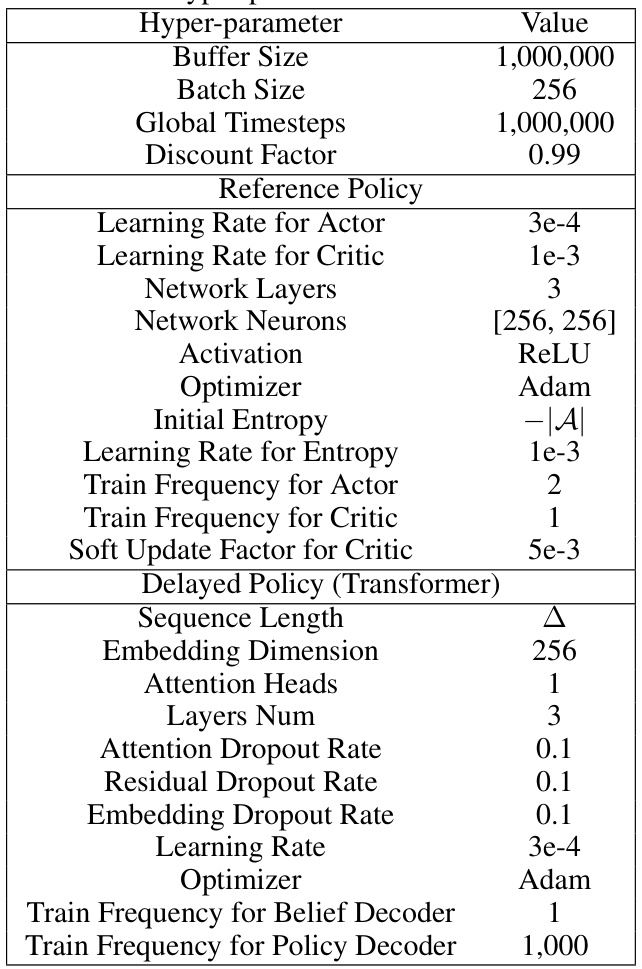
This table lists the hyperparameters used in the Variational Delayed Policy Optimization (VDPO) algorithm. It includes settings for buffer size, batch size, global timesteps, discount factor, learning rates for actor and critic, network layers and neurons, activation function, optimizer, initial entropy, entropy learning rate, training frequencies for actor and critic, soft update factor for the critic, sequence length, embedding dimension, attention heads, number of layers, dropout rates for attention, residual, and embedding, and training frequencies for the belief and policy decoders.
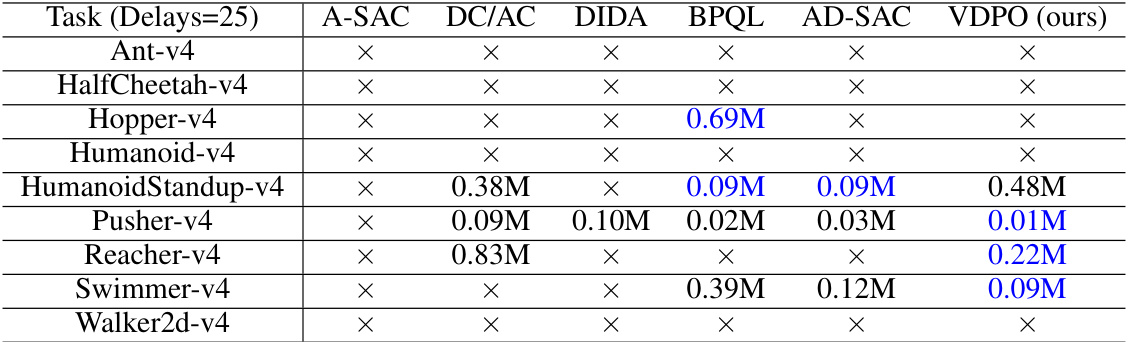
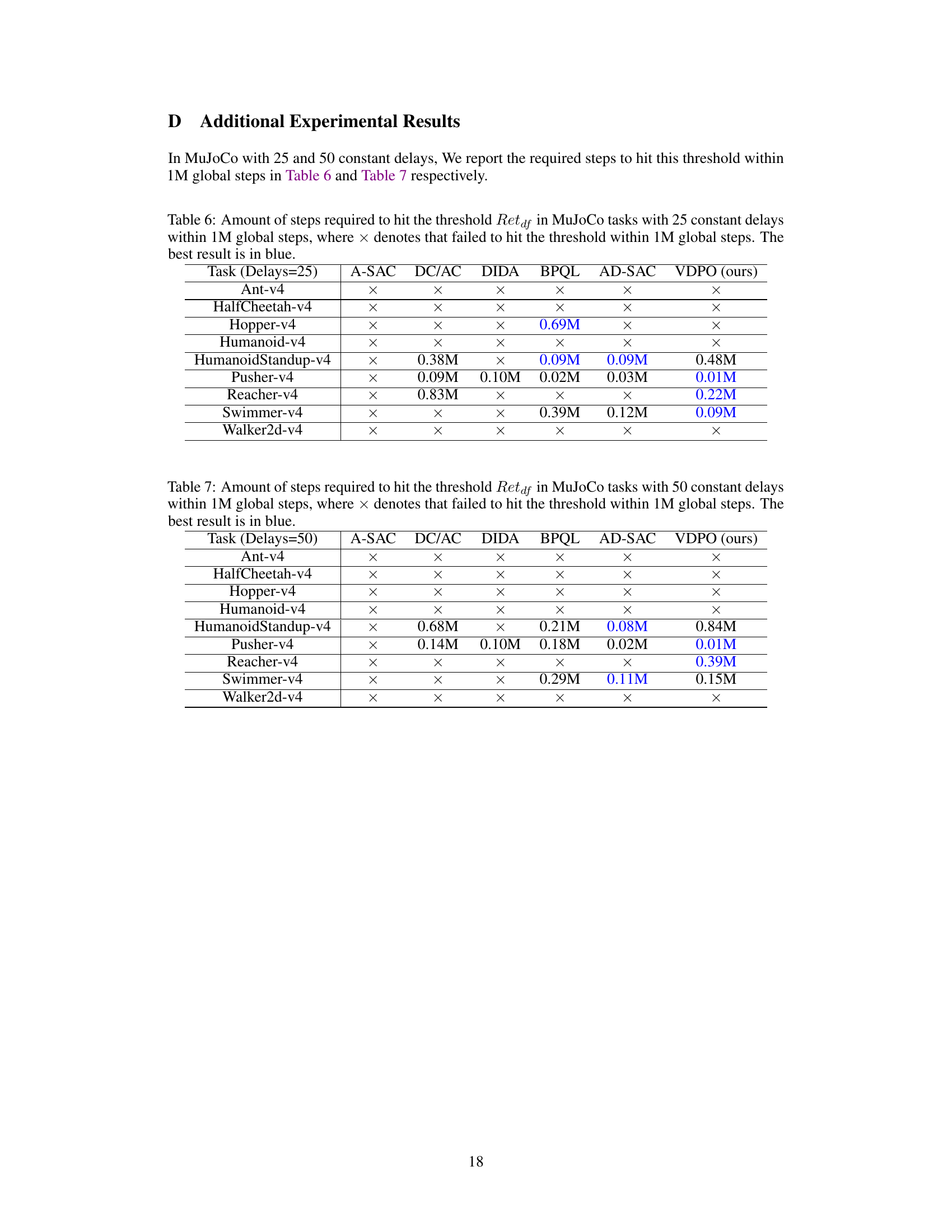
This table presents the sample efficiency results for nine MuJoCo tasks with a constant delay of 25. It shows the number of steps required by VDPO and several other algorithms (A-SAC, DC/AC, DIDA, BPQL, AD-SAC) to reach a performance threshold (Retaf) defined as the performance of a delay-free policy trained by SAC. A value of ‘x’ indicates that the algorithm failed to reach the threshold within the 1 million global steps limit. The best performance for each task is highlighted in blue, demonstrating VDPO’s superior sample efficiency compared to other methods in most tasks.
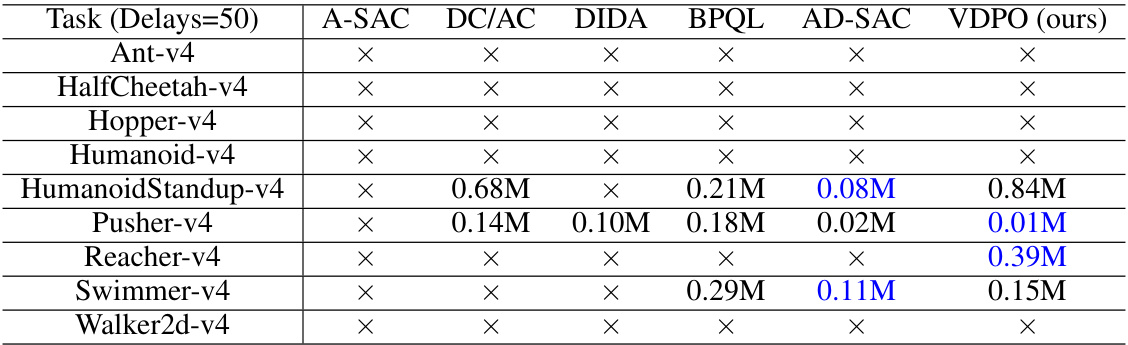
This table shows the sample efficiency results for the MuJoCo benchmark with 50 constant delays. It reports the number of steps required by different algorithms (A-SAC, DC/AC, DIDA, BPQL, AD-SAC, and VDPO) to reach a performance threshold (Retaf) within a maximum of 1 million global steps. A value of ‘x’ indicates that the algorithm failed to reach the threshold within the time limit. The best performance for each task is highlighted in blue, demonstrating the superior sample efficiency of VDPO in many cases.
Full paper#