↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Deep reinforcement learning agents often struggle with generalization to unseen environments. Unsupervised environment design (UED) aims to address this by automatically generating diverse training environments tailored to the agent’s capabilities. However, existing UED methods suffer from limitations in environment generation diversity and sample efficiency.
This paper introduces ADD (Adversarial Environment Design via Regret-Guided Diffusion Models), a novel UED algorithm that uses diffusion models to directly generate environments. ADD guides the environment generation process using the agent’s regret, enabling it to produce challenging but effective environments. ADD combines strengths of prior learning-based and replay-based methods, improving the training and generalization ability of agents. Experimental results demonstrate that ADD significantly outperforms existing UED baselines in several challenging tasks, producing more effective and diverse training environments.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and efficient method for unsupervised environment design (UED), a crucial area in reinforcement learning. ADD effectively combines the strengths of previous UED approaches while addressing their limitations, leading to significant improvements in the robustness and generalization capabilities of trained agents. The use of diffusion models and regret-guided sampling offers a new avenue for generating challenging yet instructive training environments and is highly relevant to current trends in AI and RL. The results demonstrate strong potential for improving RL algorithms and for creating better benchmarks for evaluating RL agents.
Visual Insights#
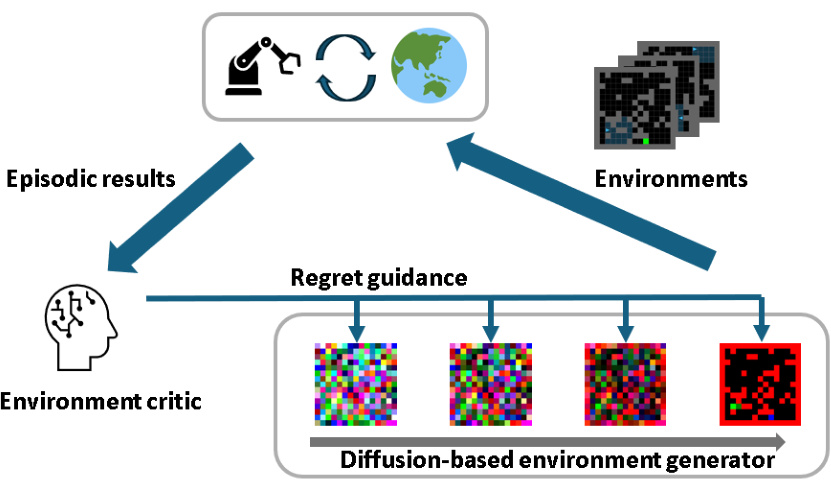
This figure illustrates the ADD (Adversarial Environment Design via Regret-Guided Diffusion Models) framework. It shows a closed-loop system where an agent interacts with environments generated by a diffusion model. The agent’s performance, measured as regret, is fed back into the system to guide the diffusion model’s generation of new, more challenging environments. This iterative process allows the agent to learn a robust policy that generalizes well to unseen environments.

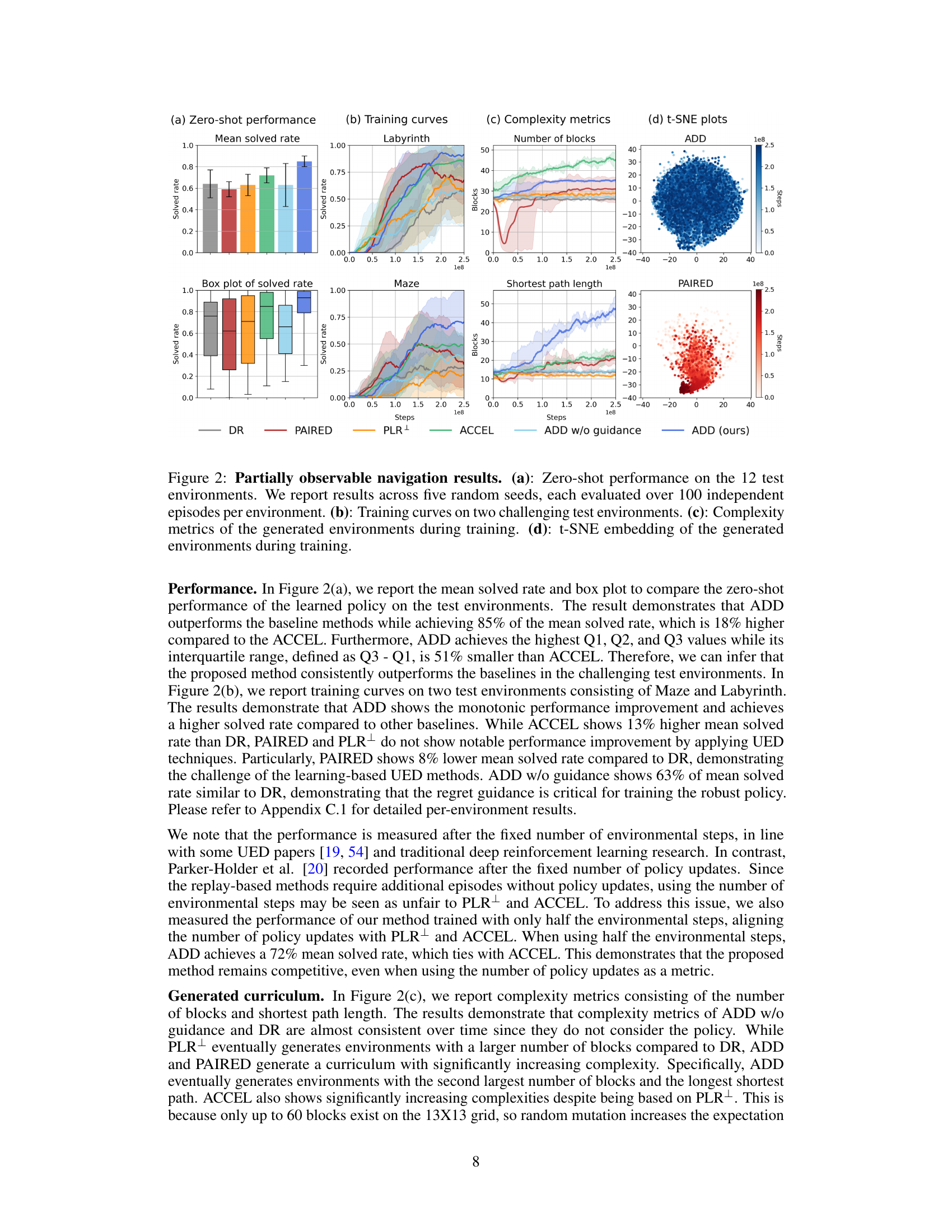
This table presents the zero-shot performance results of different reinforcement learning algorithms on twelve unseen test environments in a partially observable navigation task. The results are averages over five independent runs, each consisting of 100 independent episodes per environment. All algorithms used LSTM-based Proximal Policy Optimization (PPO) and were evaluated after 250 million environmental steps. The table provides a detailed comparison across different algorithms (DR, PAIRED, PLR+, ACCEL, ADD without guidance, and ADD) and their performance on each environment, allowing for a comprehensive evaluation of zero-shot generalization capabilities.
In-depth insights#
Robust Agent Training#
Robust agent training focuses on developing reinforcement learning (RL) agents capable of generalizing well to unseen environments and adapting to unexpected situations. This is crucial because RL agents often struggle with distribution shifts, exhibiting poor performance when tested outside their training conditions. Approaches to enhance robustness include domain randomization, which exposes the agent to a wide variety of training scenarios; adversarial training, which pits the agent against an opponent aiming to create challenging environments; curriculum learning, gradually increasing the difficulty of the training tasks; and unsupervised environment design, generating training environments based on the agent’s current capabilities and limitations. Combining these methods is a promising research direction to produce RL agents capable of handling complex, dynamic, and uncertain environments. Careful evaluation metrics, beyond simple performance scores on known tasks, are essential to truly gauge robustness, including testing across various out-of-distribution environments. Furthermore, it’s vital to consider the computational costs and sample efficiency of different robustness methods, as many require extensive simulation time and data.
Regret-Guided Diffusion#
Regret-guided diffusion presents a novel approach to unsupervised environment design (UED) by leveraging the power of diffusion models. Instead of relying solely on reinforcement learning to train an environment generator, this method directly guides the diffusion process using the agent’s regret. This allows for more efficient generation of challenging yet instructive environments, overcoming limitations of previous learning-based UED approaches. The use of regret as a guidance signal ensures that generated environments push the agent’s capabilities, promoting better generalization. The integration of diffusion models allows for the creation of diverse and complex environments, which further enhances the agent’s robustness and adaptability. This approach combines the strengths of learning-based and replay-based UED methods, achieving sample efficiency and direct environment generation. A key innovation is the development of a differentiable regret estimation technique, enabling the seamless integration of regret into the diffusion model’s learning process. Overall, regret-guided diffusion offers a powerful and flexible framework for UED, creating a more effective curriculum that leads to significantly improved generalization performance.
ADD Algorithm Details#
The ADD algorithm, detailed in the provided research paper, presents a novel approach to unsupervised environment design (UED). It leverages diffusion models, a powerful class of generative models, to dynamically create challenging environments for reinforcement learning agents. Unlike prior methods, ADD directly incorporates the agent’s regret into the environment generation process. This regret-guided approach ensures that the generated environments are not only diverse but also specifically tailored to push the agent’s learning boundaries. A crucial element is the method for estimating regret in a differentiable manner, enabling efficient gradient-based optimization within the diffusion model framework. The algorithm carefully balances exploration and exploitation, maintaining environmental diversity while focusing the agent’s learning on the most impactful areas. Furthermore, the inclusion of an entropy regularization term enhances the diversity of generated environments. ADD offers a more sample-efficient and robust method for UED than earlier learning- or replay-based approaches, potentially leading to more robust and generalizable policies for reinforcement learning agents. The ability to control the difficulty of generated environments further enhances its practical utility.
Zero-Shot Generalization#
Zero-shot generalization, the ability of a model to perform well on unseen tasks or data without any specific training, is a highly sought-after goal in machine learning. This capability is crucial for building robust and adaptable AI systems that can generalize beyond their initial training environments. Successfully achieving zero-shot generalization often requires careful consideration of model architecture, training techniques, and data representation. One major challenge lies in designing models that can effectively capture underlying patterns and relationships in data, enabling them to transfer knowledge to novel situations. Another critical aspect is the creation of diverse and representative training datasets that expose the model to a broad range of variations. This prevents overfitting to the training data and facilitates generalization. Different approaches, including few-shot learning, transfer learning, and meta-learning, can enhance zero-shot generalization but often come with limitations and tradeoffs. Ultimately, the success of zero-shot generalization depends on the model’s capacity to learn abstract concepts, reasoning capabilities, and domain knowledge. Achieving true zero-shot generalization remains a significant area of active research, promising to unlock breakthroughs in AI’s ability to tackle real-world challenges.
Future of UED Research#
The future of Unsupervised Environment Design (UED) research is bright, with several promising avenues for exploration. Improving the efficiency and scalability of UED algorithms is crucial, as current methods can be computationally expensive and may struggle with high-dimensional environments. Developing more robust and differentiable regret estimation methods would significantly enhance the performance of UED, especially when coupled with powerful generative models such as diffusion models. The integration of advanced reinforcement learning techniques, such as multi-agent reinforcement learning and hierarchical reinforcement learning, promises to enable more sophisticated and adaptable curriculum generation. Furthermore, research into new ways to evaluate the effectiveness of generated environments is needed. Existing metrics, such as zero-shot generalization, may not fully capture the nuances of an effective curriculum. Finally, exploring the applications of UED in safety-critical domains like robotics and autonomous driving holds significant potential. Addressing the challenges of generalization, safety, and robustness within these domains will require innovative approaches to UED. As the field matures, we can expect more powerful and efficient UED algorithms, leading to better generalization and more robust AI agents.
More visual insights#
More on figures
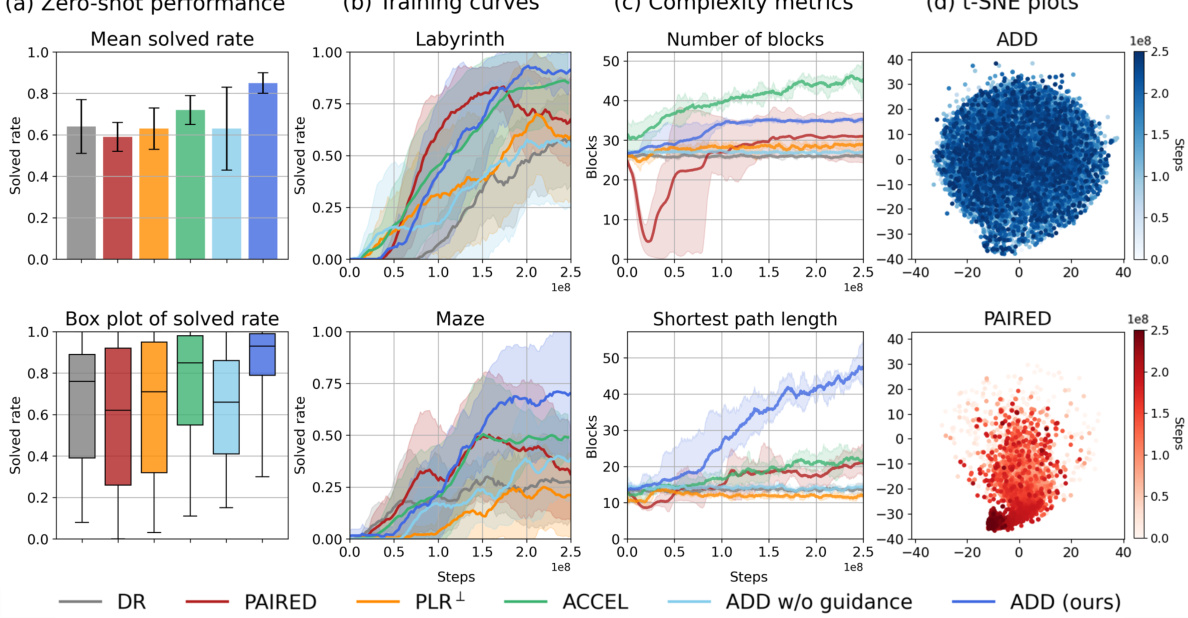
This figure presents the results of the partially observable navigation task. Subfigure (a) shows the zero-shot performance of the trained agent on 12 unseen test environments, with results averaged over five random seeds and 100 episodes per environment. Subfigure (b) displays the training curves for two challenging test environments (Labyrinth and Maze), illustrating the learning progress of different methods. Subfigure (c) presents complexity metrics (number of blocks and shortest path length) of generated environments across training iterations, showing the curriculum generated by various methods. Lastly, subfigure (d) visualizes the generated environments using t-SNE embeddings, demonstrating the diversity of environments explored by each approach.
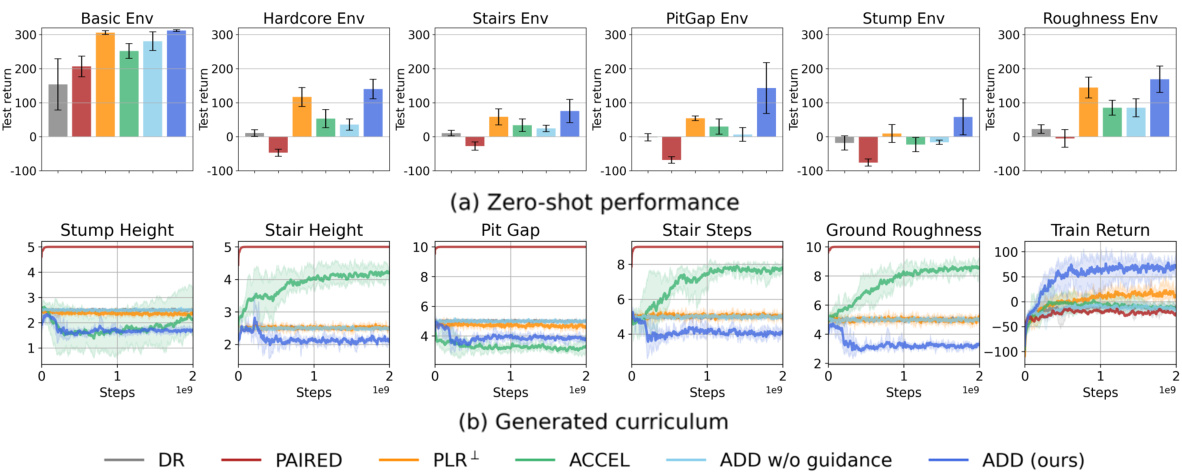
This figure shows the results of the 2D bipedal locomotion experiments. Subfigure (a) presents a bar chart comparing the zero-shot performance (average return over 100 episodes per environment, across five random seeds) of different reinforcement learning algorithms on six test environments. Subfigure (b) displays line graphs tracking several complexity metrics (stump height, stair height, pit gap, stair steps, ground roughness) of the training environments generated by each algorithm, alongside the episodic return achieved during training. The algorithms are compared against domain randomization (DR) as a baseline.

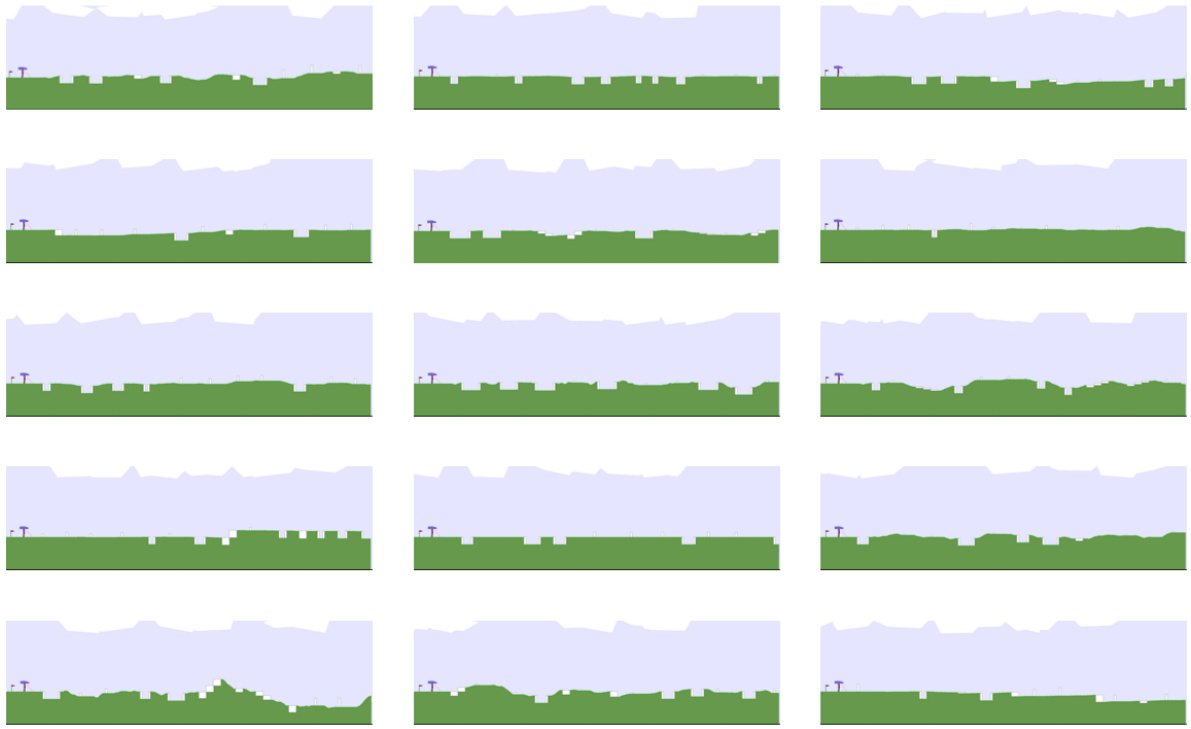
This figure shows 18 example environments generated by the algorithm at the beginning of the agent’s training in the partially observable navigation task. It visually demonstrates the initial environments generated for the agent to learn from. These are relatively simple mazes, setting the stage for the progressively more challenging environments that will be generated as training progresses.

This figure shows how the diffusion model generates maze environments. The maze is represented as a 13x13x3 tensor where each channel represents walls, agent, and goal. The model, trained on random mazes, generates new ones by reversing a diffusion process, starting from noise and guided by the learned score function.
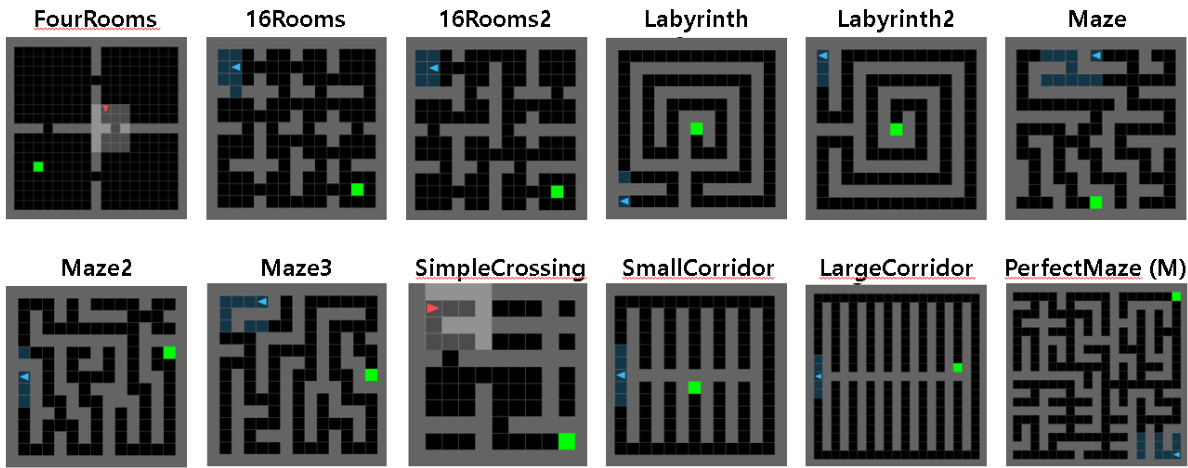
This figure shows the twelve unseen test environments used to evaluate the zero-shot generalization performance of the trained RL agent in the partially observable navigation task. The environments vary in complexity, with some being simple and others more complex. The environments from Chevalier-Boisvert et al. [53] and Jiang et al. [19, 20] provide a diverse range of challenges for the agent.

This figure shows 18 example environments generated at the beginning of the agent’s training in the partially observable navigation task. These are generated immediately after the training begins. The images show a variety of maze layouts with varying degrees of complexity and openness. The agent starts at the light blue triangle and needs to navigate to the green square.

This figure shows 18 example maze environments generated by the proposed ADD algorithm at the very beginning of agent training. The agent starts learning, and the environments are generated, showcasing the initial conditions. The green square represents the goal, the blue triangle the agent, and the black squares the walls of the maze.

This figure shows t-SNE plots visualizing the training environments generated by different methods in the partially observable navigation task. The dimensionality reduction technique t-SNE is applied to the latent space representations of the environments after encoding them with the environment critic’s encoder. The plots provide a visual comparison of environment diversity and distribution across methods such as ADD, DR, PAIRED, PLR+, ACCEL, and ADD without guidance, giving insights into the effectiveness of each method in generating diverse and informative training environments.
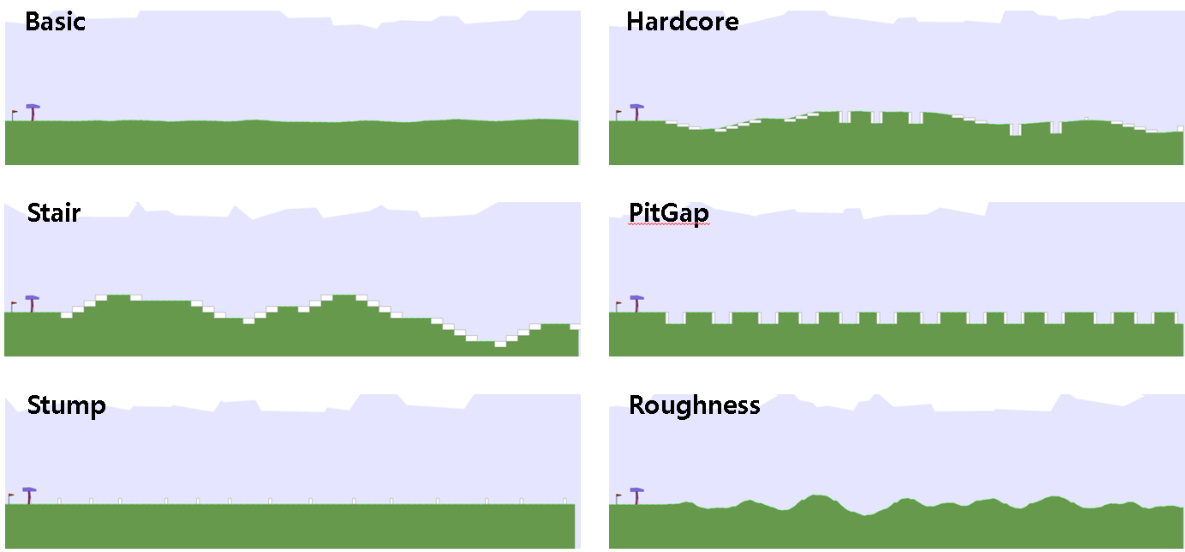
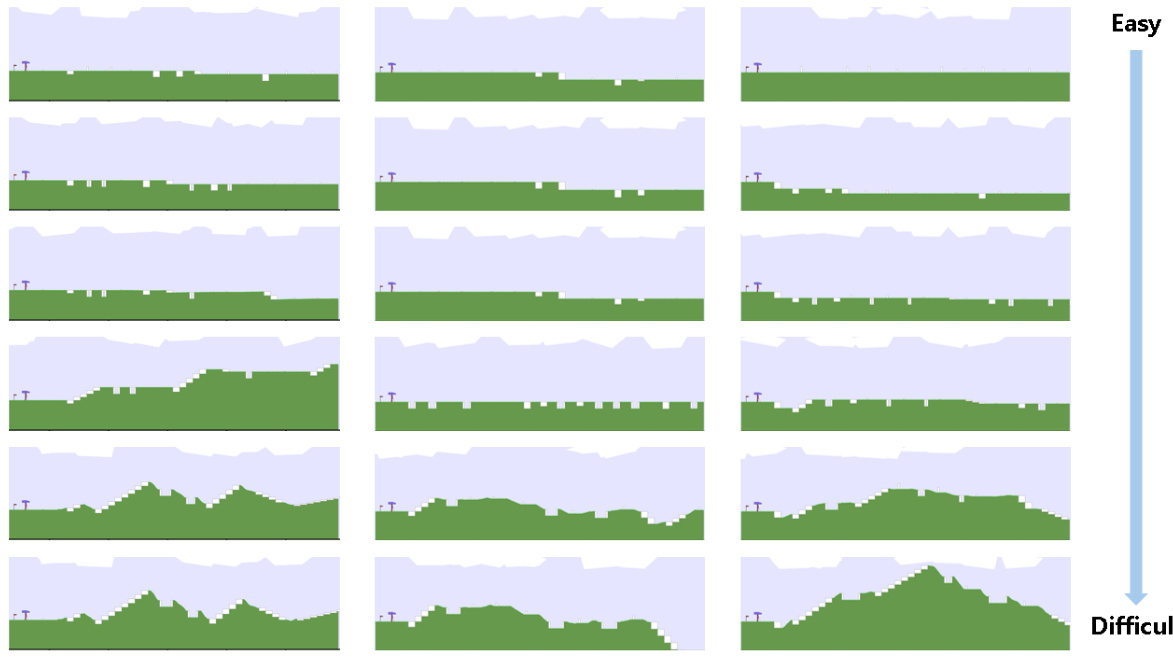
This figure shows six test environments for the 2D bipedal locomotion task. The environments vary in difficulty, ranging from a simple flat surface (Basic) to more challenging terrains including stairs, pits, stumps, and uneven ground (Hardcore, Stair, PitGap, Stump, Roughness). The Basic and Hardcore environments were sourced from OpenAI Gym [56], while the other four were adapted from a previous study by Parker Holder et al. [20]. These diverse environments are used to evaluate the generalization capabilities of the trained agents.
This figure shows a schematic overview of the Adversarial Environment Design via Regret-Guided Diffusion Models (ADD) algorithm. It illustrates the cyclical process: The agent trains on environments generated by a diffusion model, the episodic results are fed to an environment critic to estimate the agent’s regret, and this regret guides the diffusion model to generate new, more challenging environments. This loop continues until the agent develops a robust policy.
This figure illustrates the ADD (Adversarial Environment Design via Regret-Guided Diffusion Models) algorithm’s workflow. It shows how the agent, environment generator, and environment critic interact to create challenging environments for robust policy learning. The agent trains on generated environments, the environment critic assesses agent performance based on the results, and then guides the environment generator using the calculated regret to produce more challenging environments. This iterative process continues until the agent develops a robust policy that generalizes well to unseen environments.

This figure compares the diversity of training environments generated by different methods (DR, PAIRED, PLR+, ACCEL, ADD w/o guidance, and ADD) using t-SNE. t-SNE is a dimensionality reduction technique that visualizes high-dimensional data in a 2D space, allowing for a visual comparison of the distribution of the generated environments. The plot shows ADD generates a more diverse set of environments than other methods, indicating a more robust policy.
This figure shows the overall process of the proposed Adversarial Environment Design via Regret-Guided Diffusion Models (ADD) method. It illustrates how the agent, environment generator, and environment critic interact to create a curriculum of challenging environments that improve the agent’s robustness to environmental changes. The agent trains on environments generated by the diffusion model, which is guided by the regret signal from the environment critic. This critic estimates the performance difference between the current policy and the optimal policy and this difference is used to update the environment generator. The process repeats iteratively to enhance the agent’s generalization capacity.
More on tables

This table shows the range of values for each of the eight environment parameters used in the 2D bipedal locomotion task. These parameters control the difficulty of the terrain the robot must navigate. The parameters are: Stump Height, Stair Height, Pit Gap, Stair Steps, and Roughness.
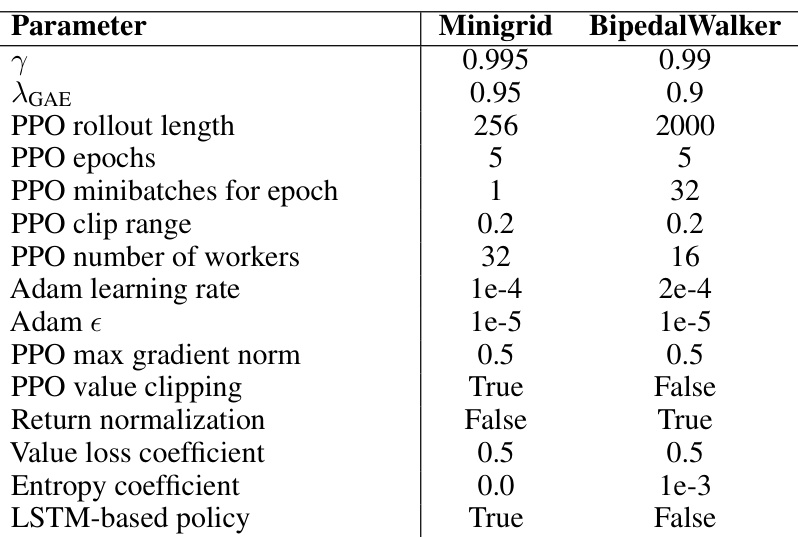
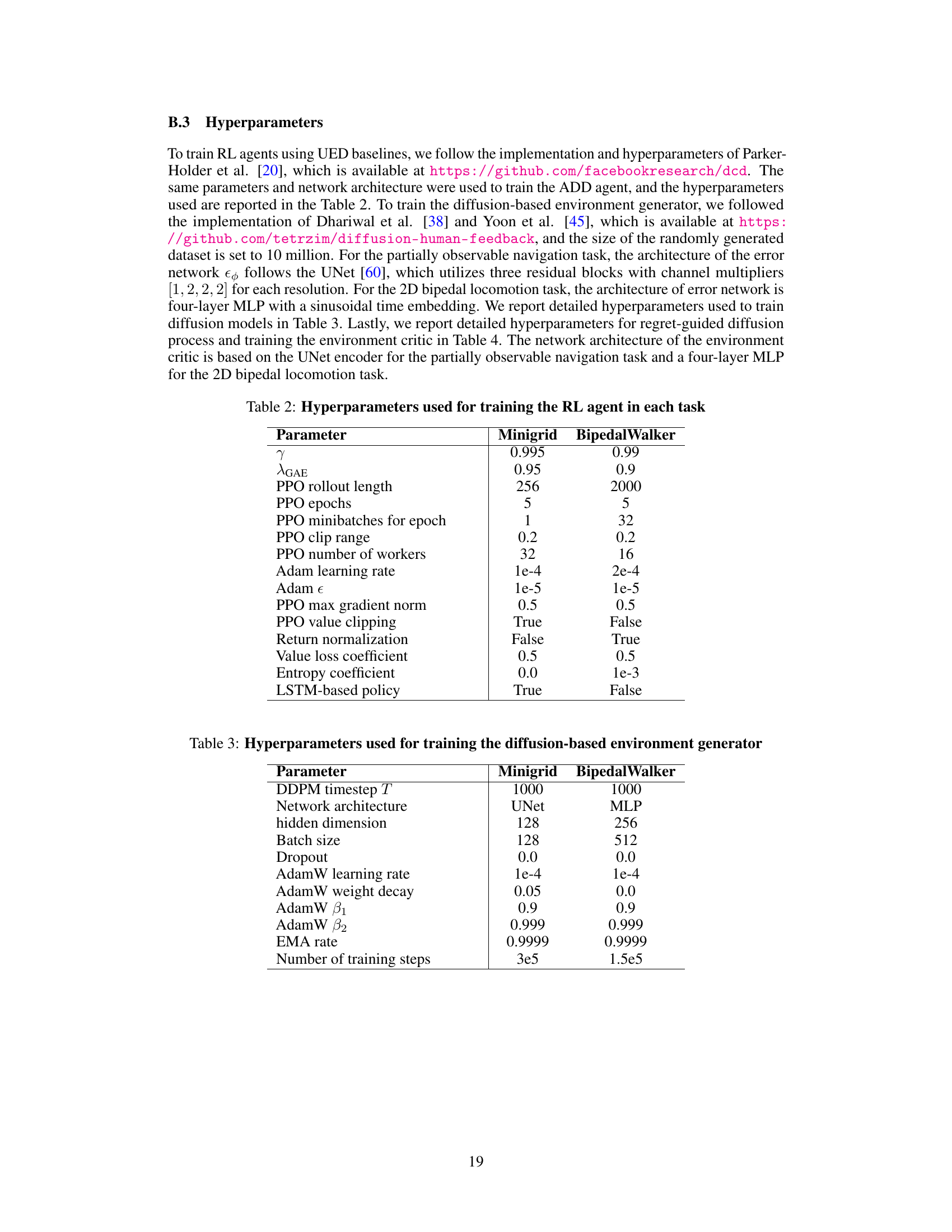
This table lists the hyperparameters used for training the reinforcement learning (RL) agent in two different tasks: Minigrid and BipedalWalker. The hyperparameters cover various aspects of the Proximal Policy Optimization (PPO) algorithm, such as the discount factor (γ), the generalized advantage estimation (GAE) parameter (λGAE), rollout length, number of epochs, and more. Differences between the two tasks are highlighted, reflecting the need for task-specific optimization strategies.
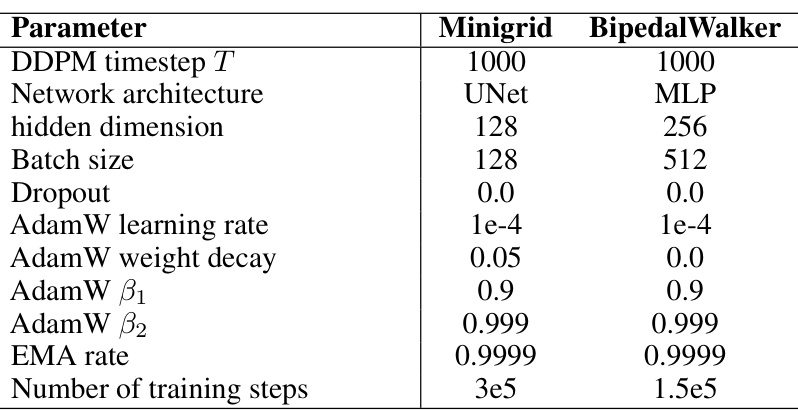
This table lists the hyperparameters used to train the diffusion-based environment generator for both the Minigrid and BipedalWalker tasks. It includes parameters for the DDPM timestep, network architecture (UNet for Minigrid, MLP for BipedalWalker), hidden dimension, batch size, dropout rate, AdamW optimizer parameters (learning rate, weight decay, beta1, beta2), EMA rate, and the total number of training steps.
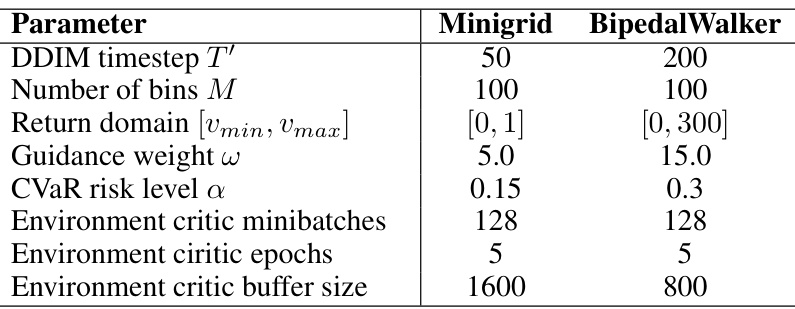
This table lists the hyperparameters used in the regret-guided diffusion model and environment critic training for both the Minigrid and BipedalWalker tasks. The hyperparameters control various aspects of the training process, including the number of denoising steps, the number of bins in the return distribution, the strength of the regret guidance, the risk level for CVaR, and the batch size and number of epochs used for training the environment critic.
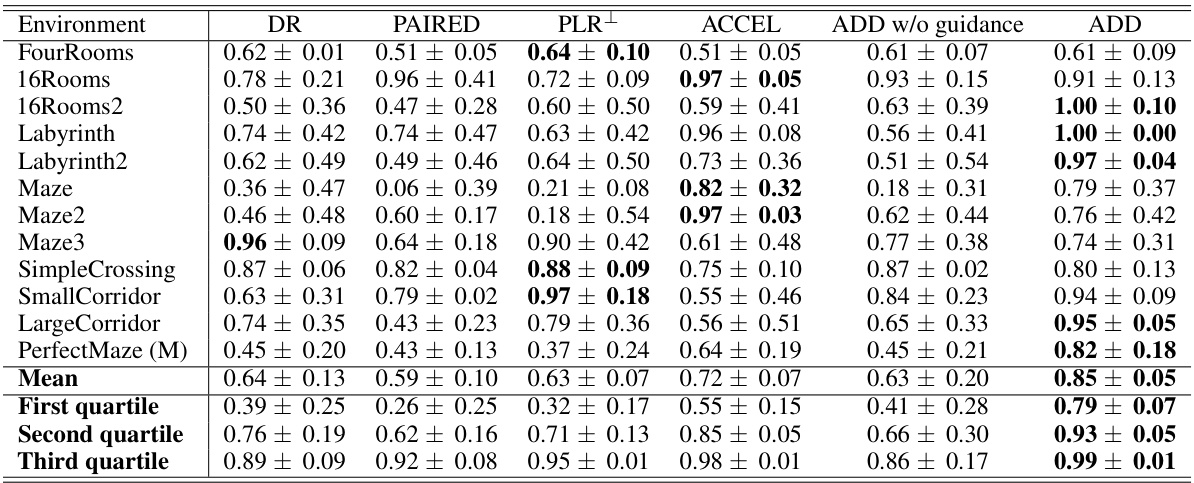
This table presents the zero-shot generalization performance of different reinforcement learning algorithms on 12 unseen test environments in a partially observable navigation task. The results, averaged over five independent runs with 100 episodes each, show the mean solved rate and standard deviation for each algorithm (DR, PAIRED, PLR+, ACCEL, ADD w/o guidance, and ADD). It highlights the superior performance of ADD compared to the baselines.

This table presents the average return and standard deviation achieved by different reinforcement learning algorithms on six test environments in a 2D bipedal locomotion task. The algorithms are compared against a domain randomization baseline. Each algorithm’s performance is evaluated over five independent runs, with each run consisting of 100 trials on each test environment. All agents were trained using the Proximal Policy Optimization (PPO) algorithm for 2 billion environmental steps.

This table presents the results of an ablation study conducted to evaluate the impact of the entropy regularization term (ω) on the performance of the proposed ADD algorithm in the partially observable navigation task. Different values of ω were tested, and the mean success rate (averaged across five independent seeds) was calculated for each. The table shows how the performance changes as the value of ω increases.
Full paper#