↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Traditional reinforcement learning (RL) research has primarily focused on algorithmic improvements to enhance sample efficiency, especially in continuous control tasks. However, these methods often struggle with complex environments and require extensive computation. This paper reveals that simply increasing model capacity, specifically the critic network size, can drastically improve performance if paired with effective regularization techniques, such as layer normalization and weight decay. Furthermore, this study also identified the crucial role of optimistic exploration in achieving near-optimal policies. Naive scaling, however, can lead to poor performance if not done correctly.
The authors introduce the BRO (Bigger, Regularized, Optimistic) algorithm, which leverages strong regularization to enable effective scaling of the critic networks. This, combined with optimistic exploration, results in state-of-the-art performance across multiple complex continuous control benchmarks. BRO outperforms all previous methods, showcasing the significance of scaling in achieving sample efficiency. The findings highlight a surprisingly effective approach that involves model scaling instead of focusing solely on algorithmic improvements. The combination of BroNet architecture, regularized critic network scaling and optimistic exploration is the key to BRO’s unprecedented sample efficiency and performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning (RL) as it challenges the conventional focus on algorithmic enhancements for sample efficiency. By demonstrating the substantial improvements achievable through model scaling with appropriate regularization, it opens new avenues for research, potentially leading to more sample-efficient and scalable RL algorithms. The findings are particularly important for continuous control tasks, where strong regularization combined with optimistic exploration significantly outperforms existing model-based and model-free algorithms. This work paves the way for more efficient RL algorithms in various fields.
Visual Insights#
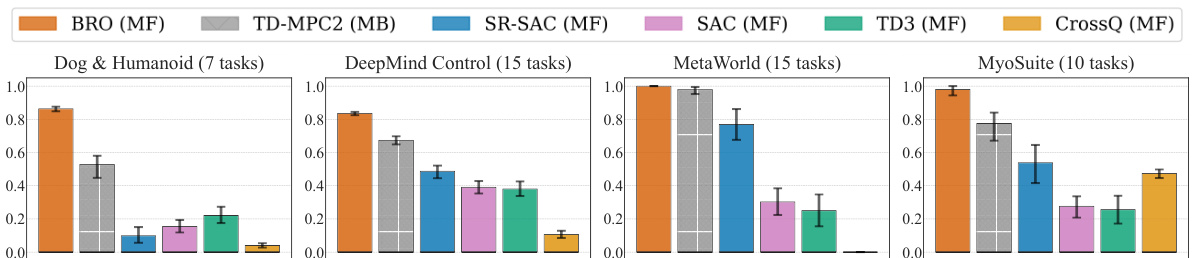
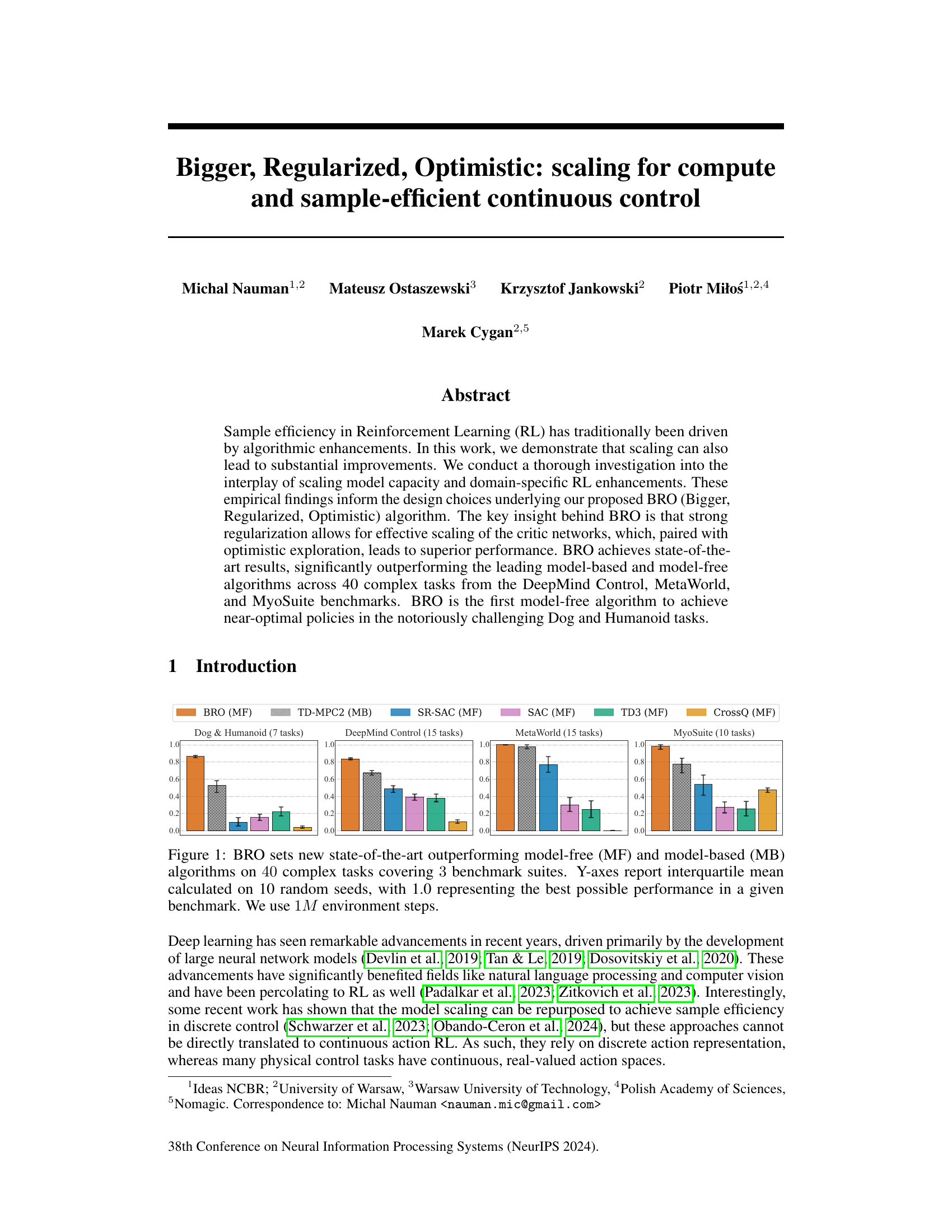
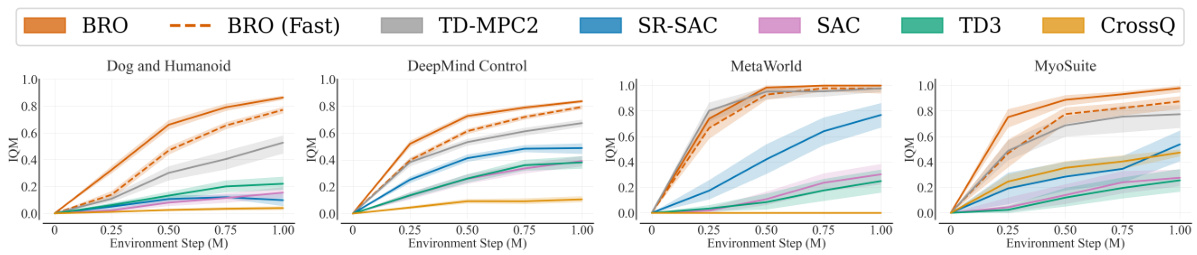
This figure compares the performance of the BRO algorithm against other model-free (MF) and model-based (MB) reinforcement learning algorithms across four benchmark suites: DeepMind Control, MetaWorld, MyoSuite, and Dog & Humanoid. BRO significantly outperforms all other algorithms across a total of 40 complex continuous control tasks. The y-axis represents the interquartile mean performance, normalized to a maximum of 1.0, based on 10 independent runs with different random seeds. All algorithms were trained for 1 million environment steps.
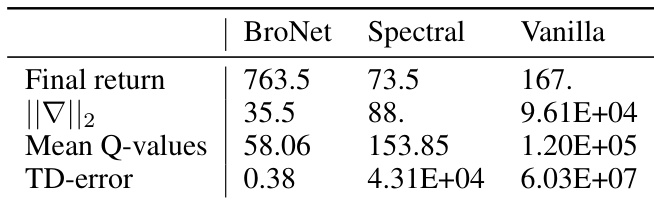
This table compares the performance of three different critic network architectures (BroNet, Spectral, and Vanilla MLP) when combined with the BRO algorithm on challenging Dog environments. It shows that BroNet significantly outperforms the others in terms of final return, gradient norm, mean Q-values, and TD-error, indicating its superior stability and performance in these complex tasks.
In-depth insights#
BRO Algorithm Design#
The BRO (Bigger, Regularized, Optimistic) algorithm’s design is centered around effectively scaling the critic network while maintaining stability and sample efficiency. This is achieved through three key components: ‘Bigger’, involving a substantial increase in critic network size (approximately 7 times larger than standard SAC); ‘Regularized’, employing techniques like layer normalization, weight decay, and full parameter resets to prevent overfitting and ensure stability during scaling; and ‘Optimistic’, using dual policy optimistic exploration and non-pessimistic Q-value approximation for effective exploration, counteracting the potential negative effects of strong regularization on exploration. The interplay between these design elements is crucial, with strong regularization enabling successful critic scaling and optimistic exploration enhancing sample efficiency in challenging continuous control tasks. The architecture is carefully crafted, using BroNet to optimize for these factors. This integrated approach allows BRO to achieve state-of-the-art performance across multiple benchmarks, demonstrating that effective scaling, combined with robust algorithmic design, can substantially advance sample efficiency in reinforcement learning.
Critic Network Scaling#
The effectiveness of scaling critic networks in reinforcement learning is a complex issue. Naive scaling often leads to performance degradation. However, the paper reveals that skillful critic scaling, when combined with strong regularization and optimistic exploration, can dramatically improve sample efficiency and overall performance. This finding challenges the conventional wisdom in continuous control, where algorithmic enhancements have been the primary focus. The authors introduce BroNet, a novel architecture designed specifically to enable effective critic scaling. They demonstrate that the benefits of critic scaling outweigh those of increased replay ratio, offering superior performance and computational efficiency. Strong regularization, specifically employing layer normalization, is crucial for achieving stable and improved scaling. Optimistic exploration, implemented through a dual policy setup, further enhances performance gains, particularly in the early stages of training. The success of BRO highlights the potential of scaling model capacity as a powerful technique for sample-efficient RL.
Sample Efficiency Gains#
The research demonstrates significant sample efficiency gains, surpassing state-of-the-art model-free and model-based algorithms across various complex continuous control tasks. This improvement stems from a novel combination of strong regularization, allowing for effective scaling of critic networks, and the use of optimistic exploration. BRO (Bigger, Regularized, Optimistic), the proposed algorithm, achieves near-optimal policies in notoriously challenging tasks, showcasing the impact of scaling model capacity alongside algorithmic enhancements. The results highlight the importance of a well-regularized large critic network for superior performance. Scaling the critic model proves far more effective than simply increasing the replay ratio, offering significant computational advantages due to the parallelisable nature of critic scaling. These findings challenge the prevailing focus on algorithmic improvements in continuous deep RL and open up new avenues for future research.
Optimistic Exploration#
The concept of “Optimistic Exploration” in reinforcement learning centers on the idea of actively encouraging exploration by overestimating the potential rewards of unvisited or less-visited states. This contrasts with purely pessimistic approaches that might overly prioritize exploitation of known good states. Optimistic methods often involve modifying the Q-value estimates (or similar reward predictions) to inflate the expected value of uncertain actions, thus biasing the agent towards trying out new things. This can be achieved through various techniques, such as using optimistic bootstrapping, employing exploration bonuses, or shaping the reward function. The success of optimistic exploration depends heavily on finding a balance. While excessive optimism could lead to inefficient random exploration, insufficient optimism could hinder the agent’s ability to discover better states. Careful tuning of the optimism parameters is crucial for optimal performance.
Future Research Needs#
Future research should address several key limitations of the current BRO approach. Scaling BRO to handle high-dimensional state and action spaces more effectively is crucial, particularly for real-world robotics applications. Current benchmarks may not fully capture the challenges of such complex environments. The impact of BRO’s design choices on different task types (e.g. discrete vs continuous) also requires further investigation. Research into more efficient inference methods (like model compression techniques) is needed to enhance real-time capabilities. Exploration of BRO’s application in offline RL settings and image-based RL could broaden its applicability. Finally, a thorough analysis of the interaction between model capacity and algorithmic enhancements is needed to maximize efficiency and generalize BRO’s success to diverse domains. Addressing these points would improve BRO’s practicality and advance the field of sample-efficient reinforcement learning.
More visual insights#
More on figures
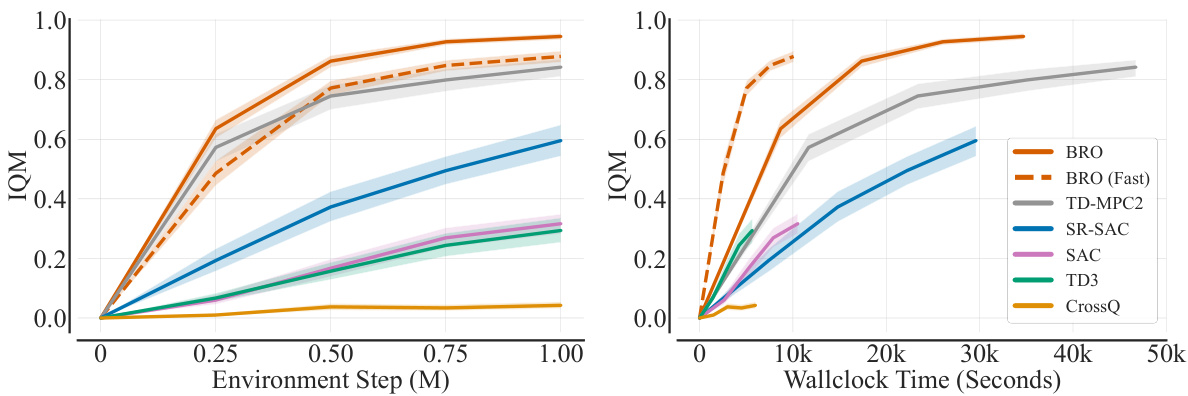
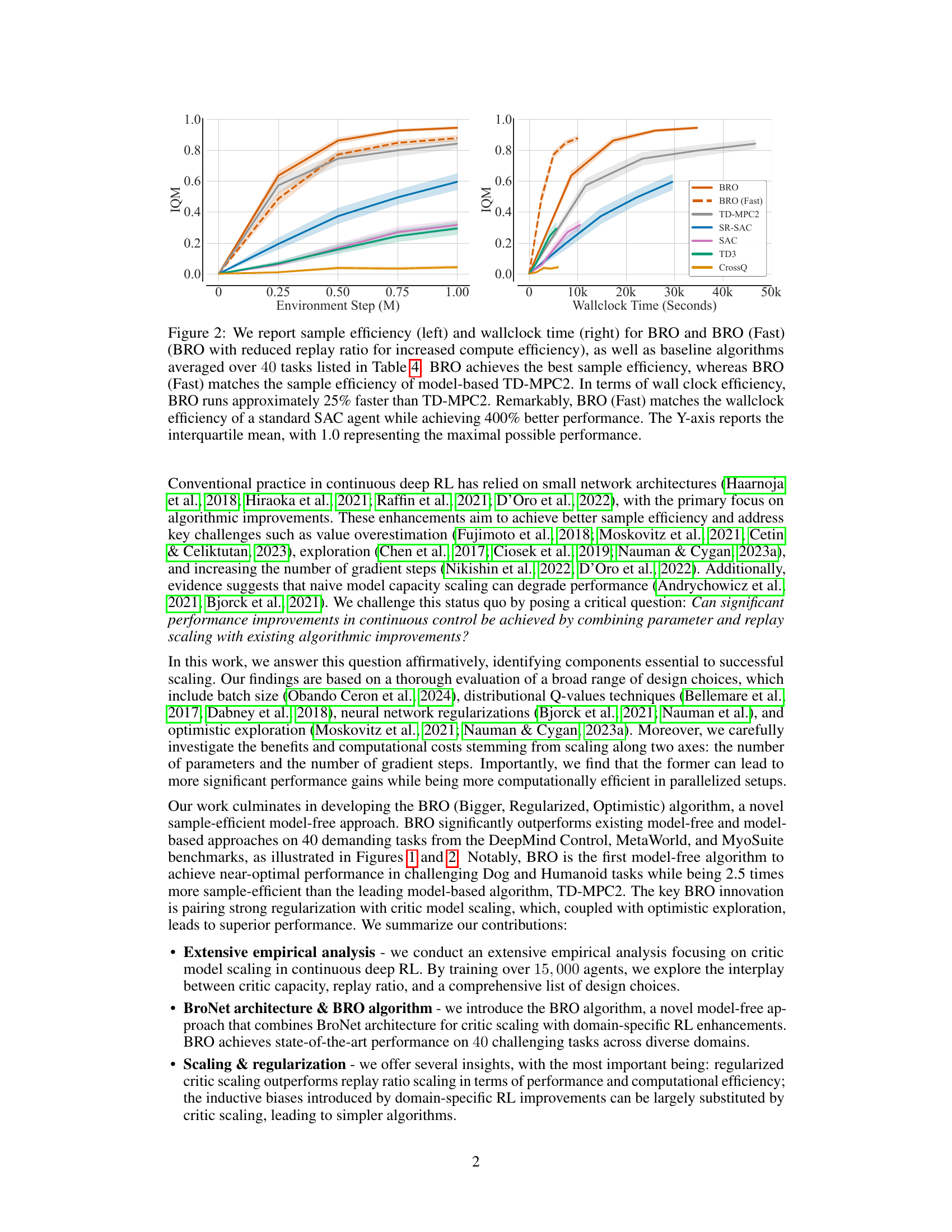
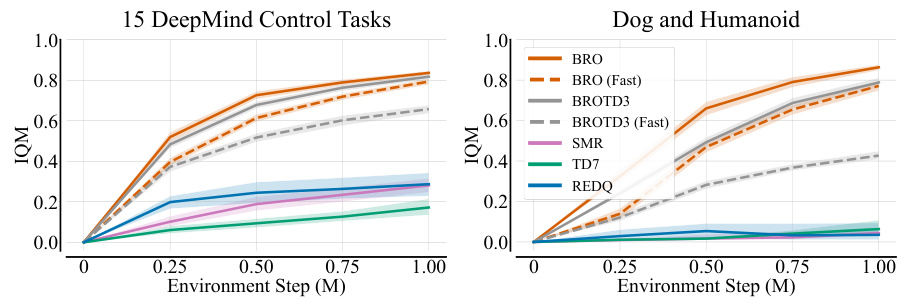
This figure shows a comparison of sample efficiency and wall-clock time for the proposed BRO algorithm and its faster variant (BRO-Fast), along with several baseline reinforcement learning algorithms. The results are averaged across 40 benchmark tasks. BRO demonstrates superior sample efficiency, while BRO-Fast achieves comparable efficiency to the model-based TD-MPC2. Notably, BRO-Fast matches SAC’s wall-clock efficiency despite achieving significantly higher performance.
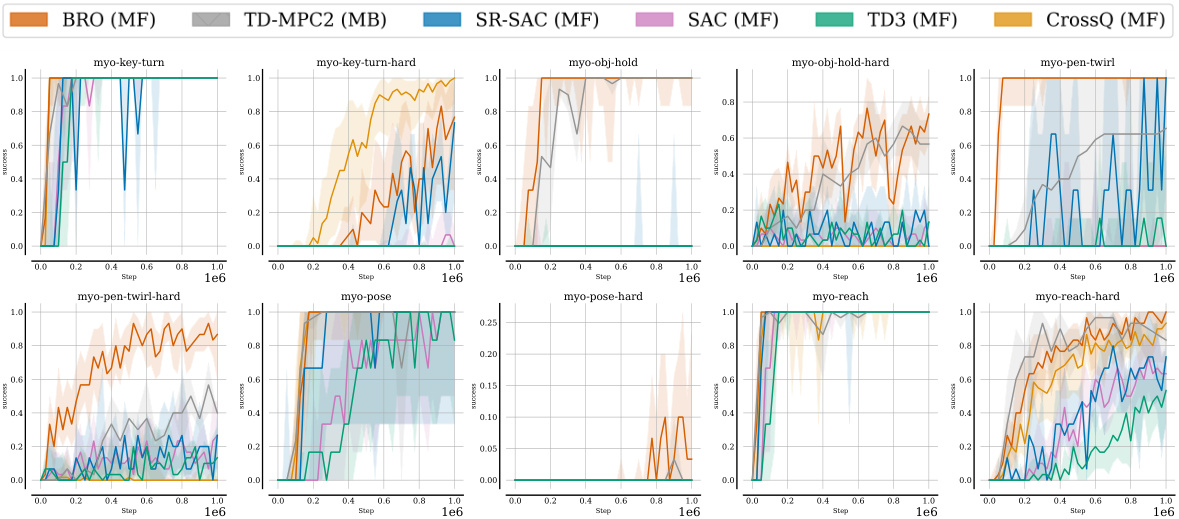
This figure compares the BRO algorithm’s performance against other model-free and model-based algorithms across three benchmark suites (DeepMind Control, MetaWorld, and MyoSuite) containing a total of 40 complex tasks. The y-axis represents the normalized interquartile mean performance (1.0 being optimal), averaged across 10 random seeds, after 1 million environment steps. The results visually demonstrate that BRO significantly outperforms the other algorithms in all three benchmark suites.
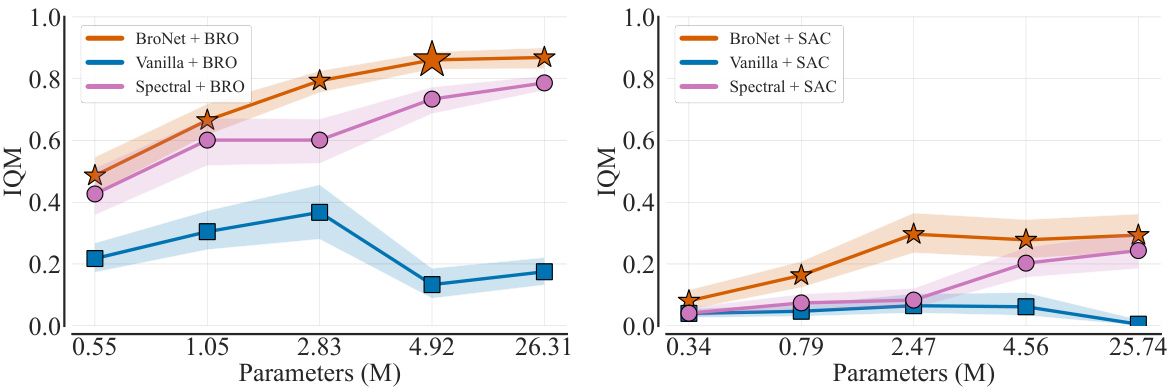
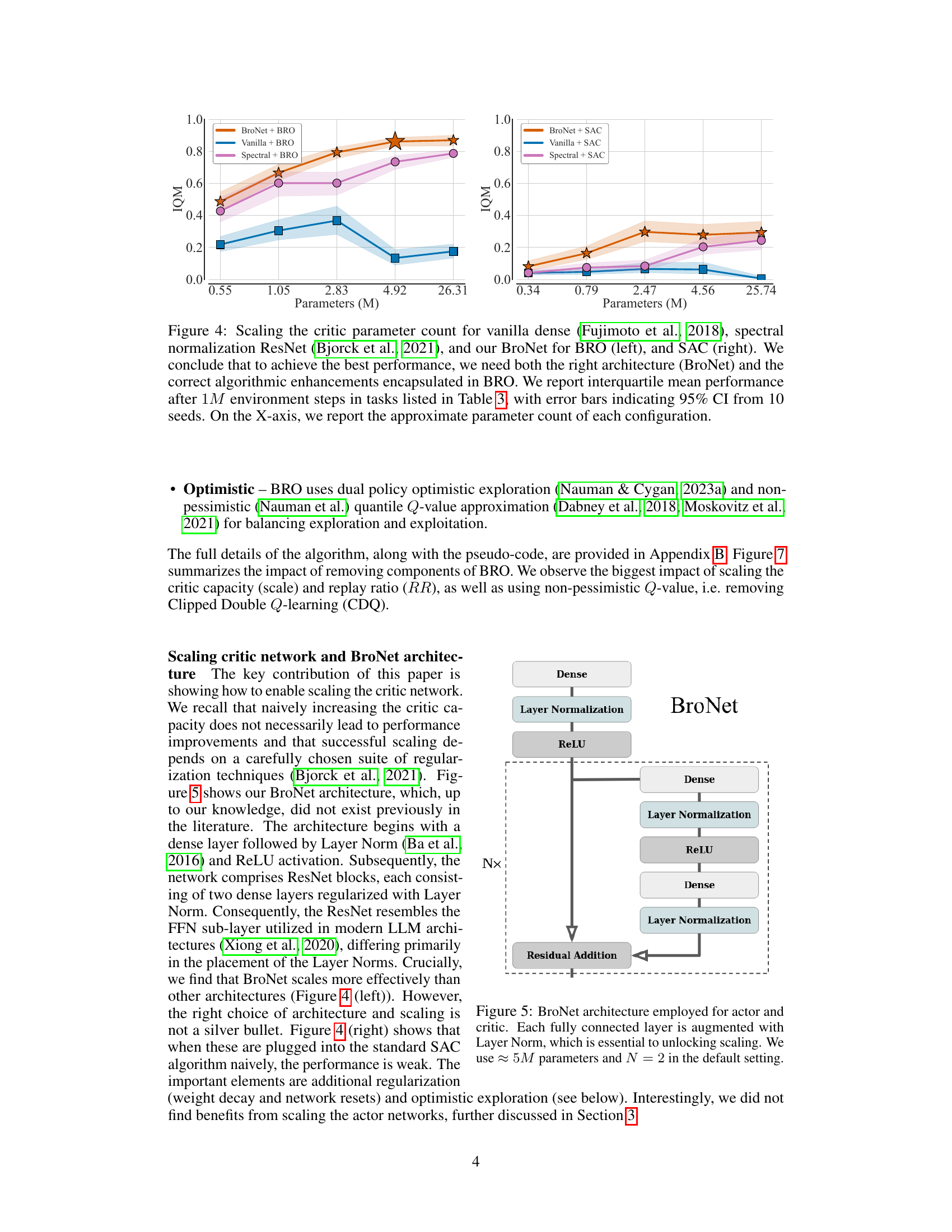
This figure shows the impact of scaling the critic network’s parameter count on the performance of different algorithms (BRO and SAC) using three different architectures: vanilla dense, spectral normalization ResNet, and BroNet. The left panel shows the results for BRO, while the right panel presents the results for SAC. The x-axis represents the approximate number of parameters in millions (M), and the y-axis shows the interquartile mean (IQM) performance. The figure demonstrates that BroNet, combined with the BRO algorithm, achieves the best performance across different parameter counts. It highlights the importance of both appropriate architecture and algorithmic enhancements for achieving superior performance in continuous control tasks.

This figure shows the architecture of BroNet, a neural network used in the BRO algorithm for both the actor and critic. The key feature is the use of Layer Normalization after each fully connected layer. This design is crucial for enabling effective scaling of the critic network which is a major part of the BRO algorithm’s success in improving sample efficiency. The figure details the structure, showing the dense layers, Layer Normalization, ReLU activation function, and residual connections (indicated by N x). The default number of parameters is approximately 5 million, and N (the number of residual blocks) is set to 2.
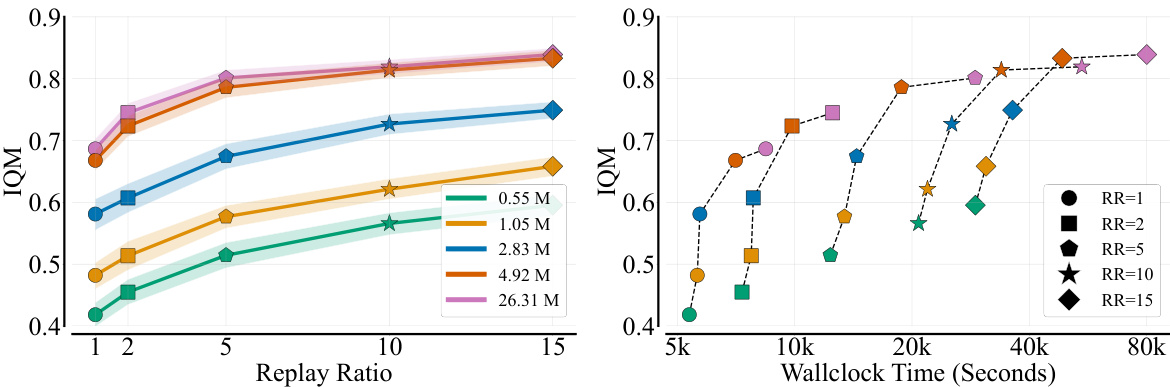
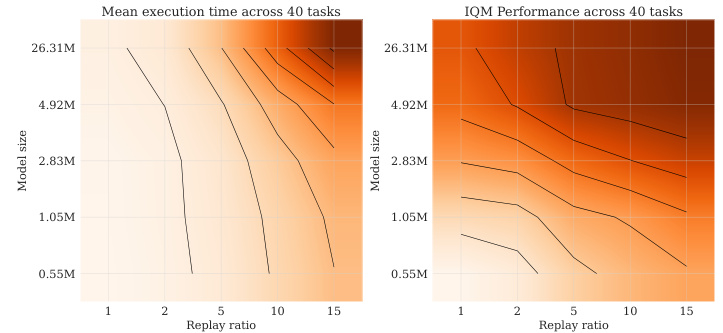
This figure shows the results of an experiment investigating the impact of scaling replay ratio and critic model size on the performance of reinforcement learning agents. The left panel shows how performance increases with both larger models and higher replay ratios. The right panel illustrates the trade-off between performance gains and computational cost when scaling using either method; increasing model size is more computationally efficient than increasing the replay ratio for achieving similar performance improvements.
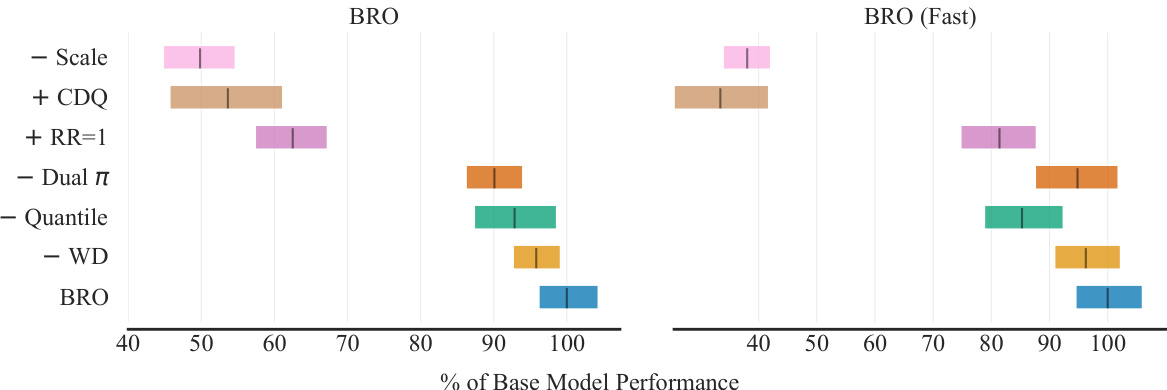
This ablation study shows the impact of each BRO component on the overall performance. Removing the critic scaling (-Scale), using pessimistic Q-learning (+CDQ), and using the standard replay ratio (+RR=1) significantly reduces the performance. Other components, such as optimistic exploration (-Dual π), quantile Q-values (-Quantile), and weight decay (-WD) show smaller, but still noticeable impact.
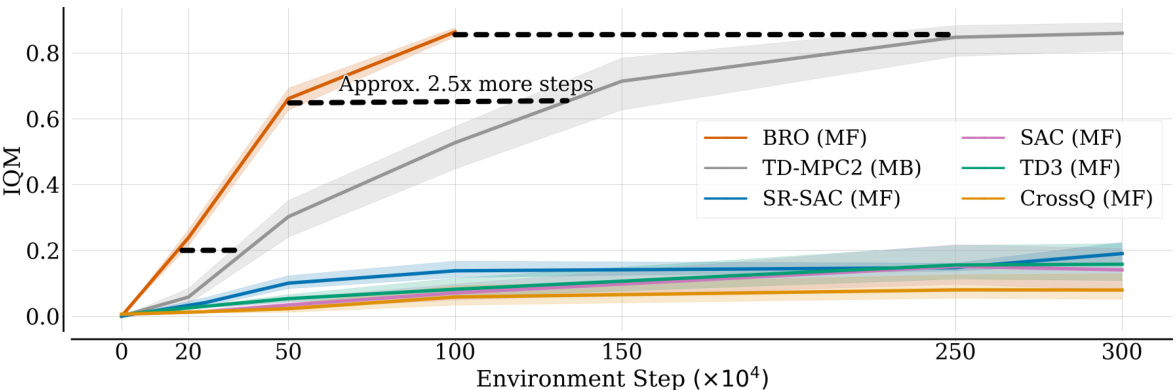
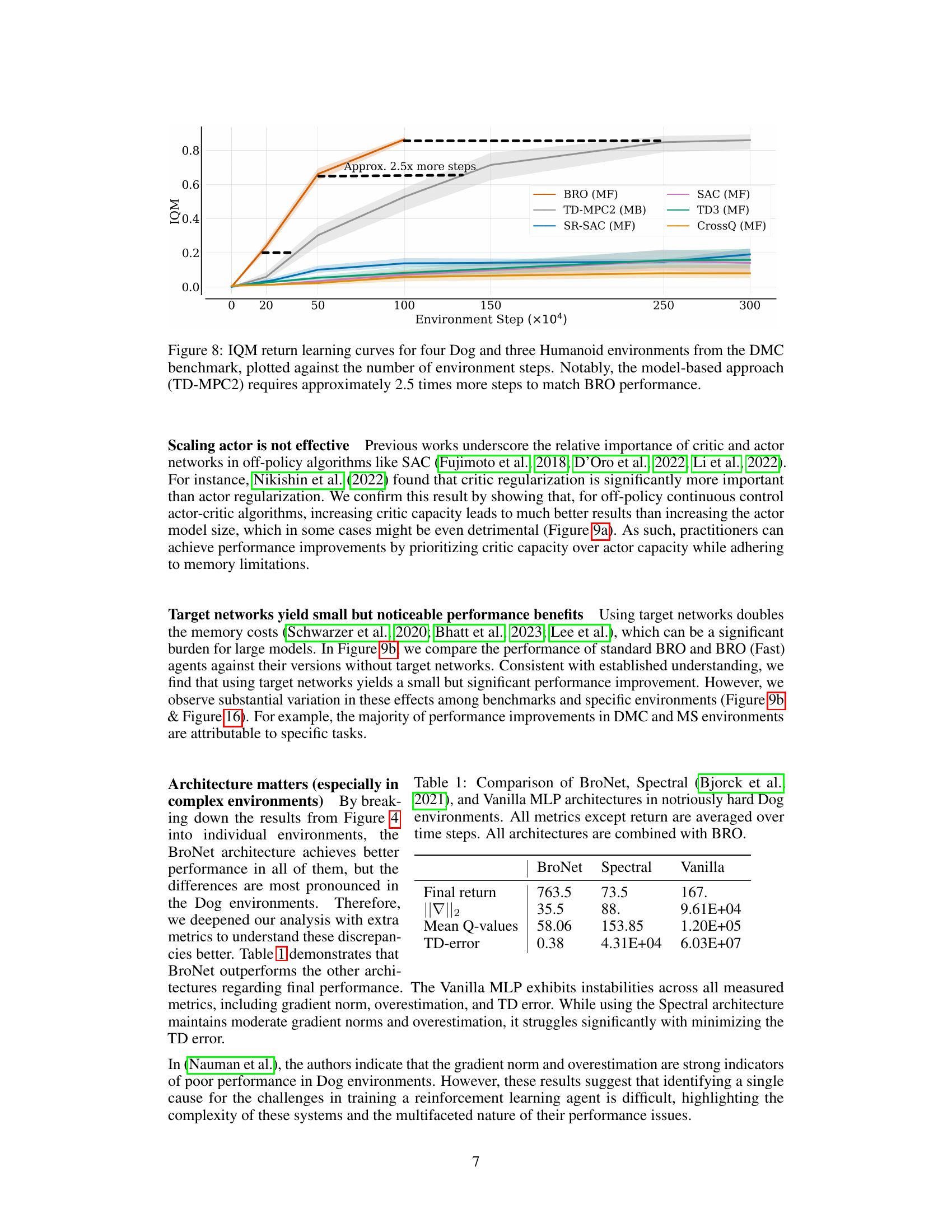
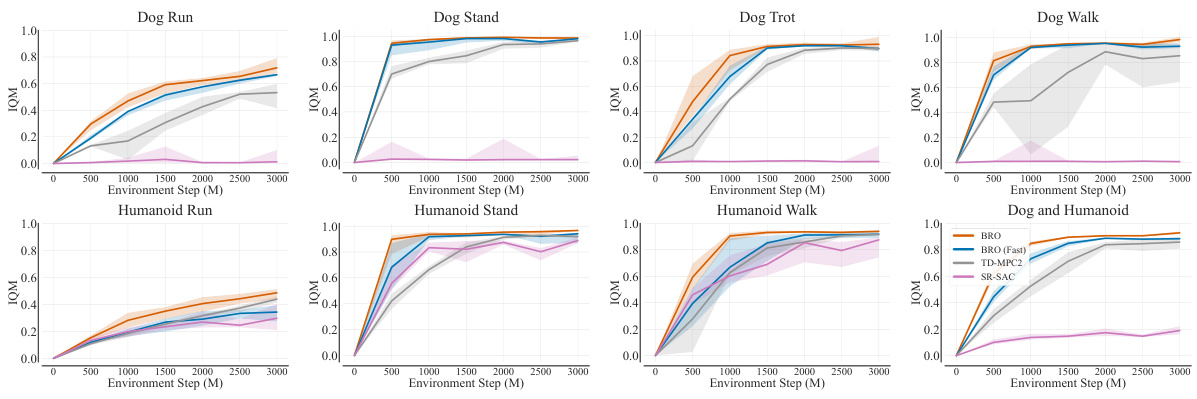
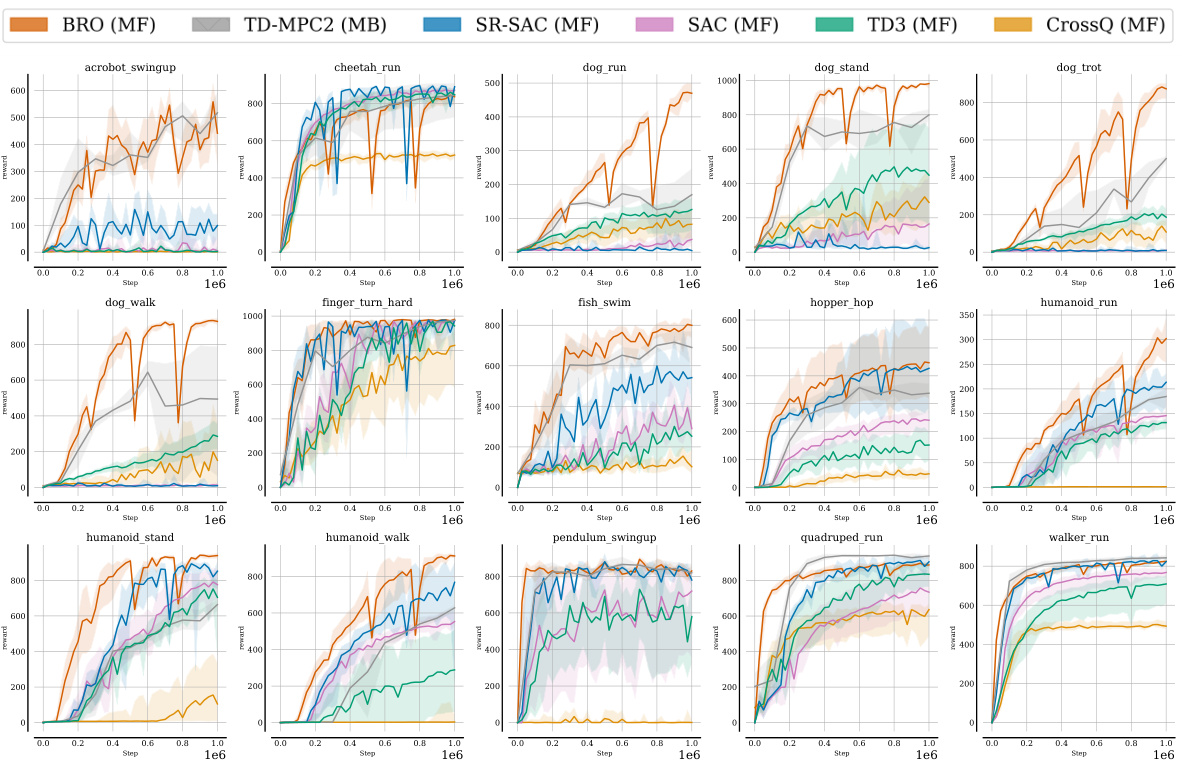
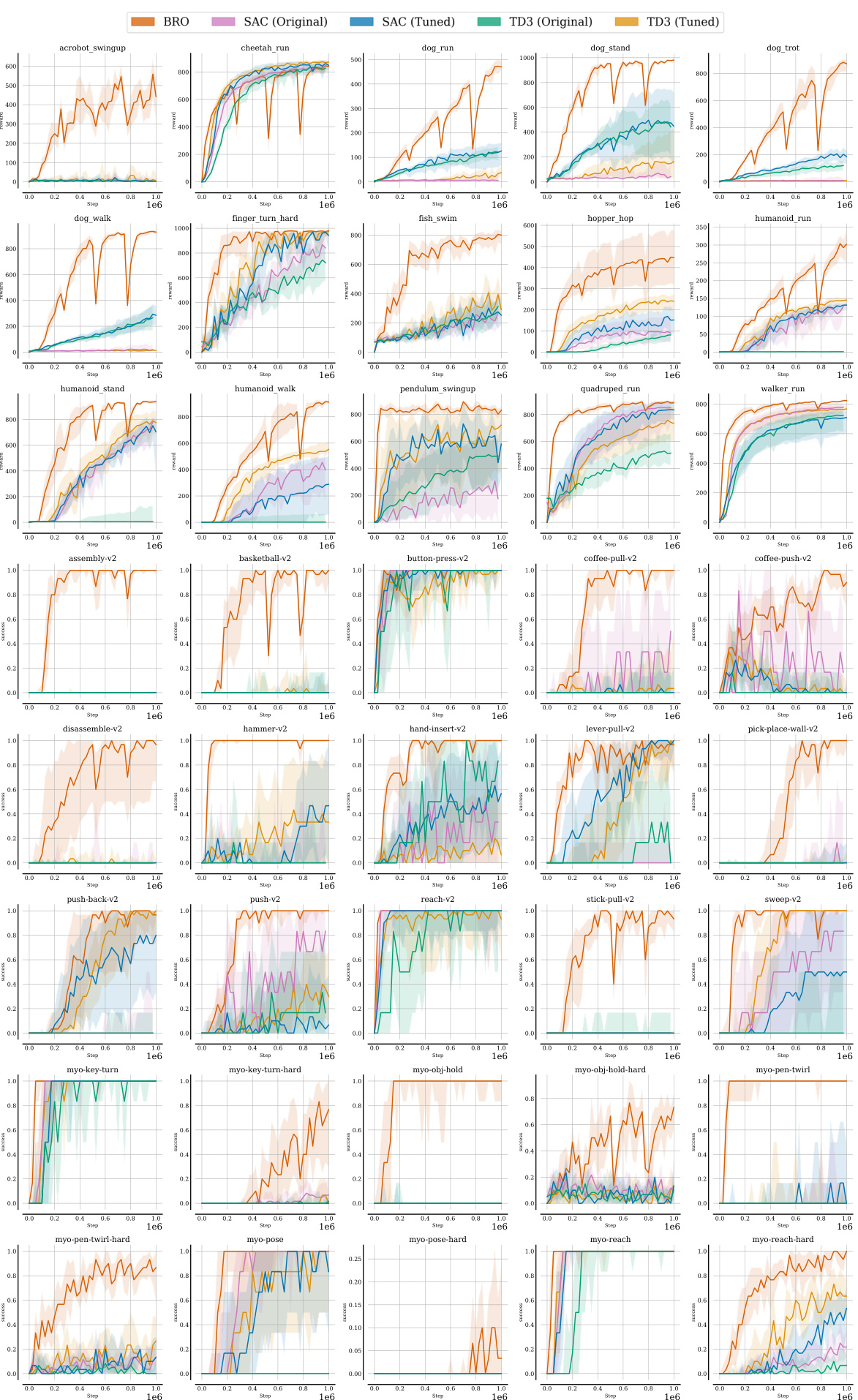
This figure shows the learning curves for several reinforcement learning algorithms on seven locomotion tasks from the DeepMind Control suite (DMC). The y-axis represents the interquartile mean (IQM) return, a measure of the average reward obtained by the agents. The x-axis represents the number of environment steps. BRO significantly outperforms all other algorithms, reaching near-optimal performance much faster. Specifically, the model-based algorithm TD-MPC2 takes about 2.5 times more steps to achieve similar results as BRO.
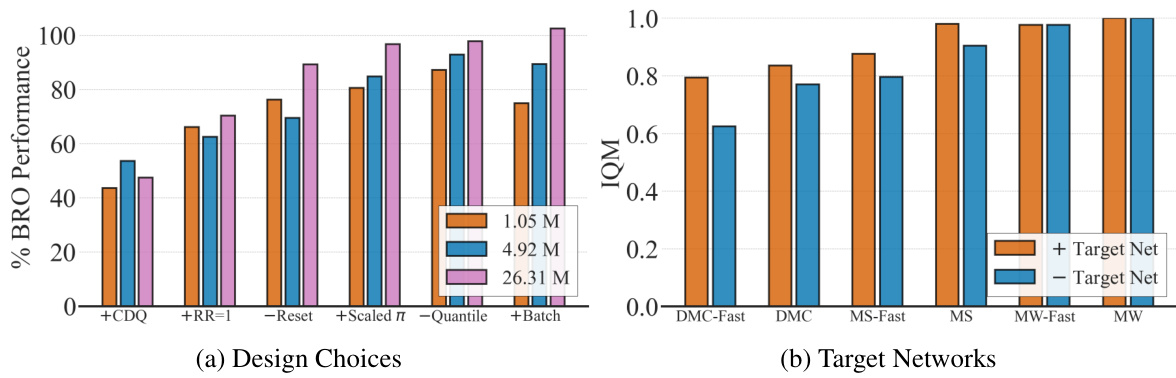
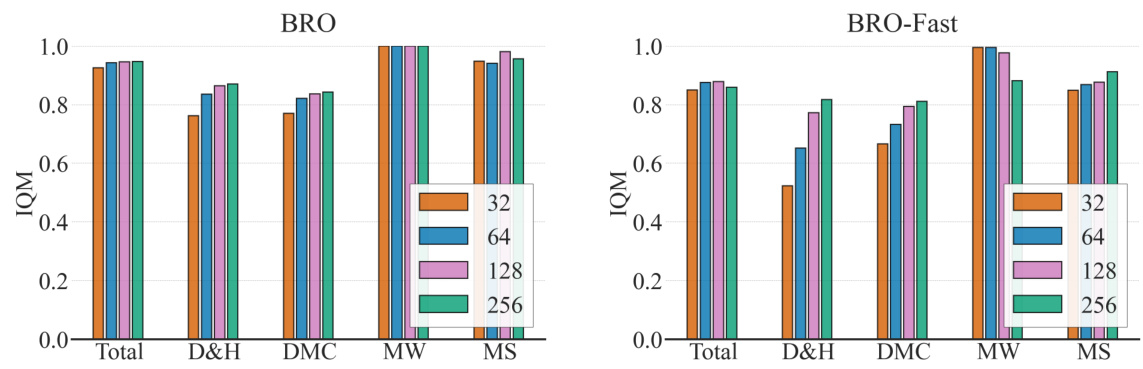
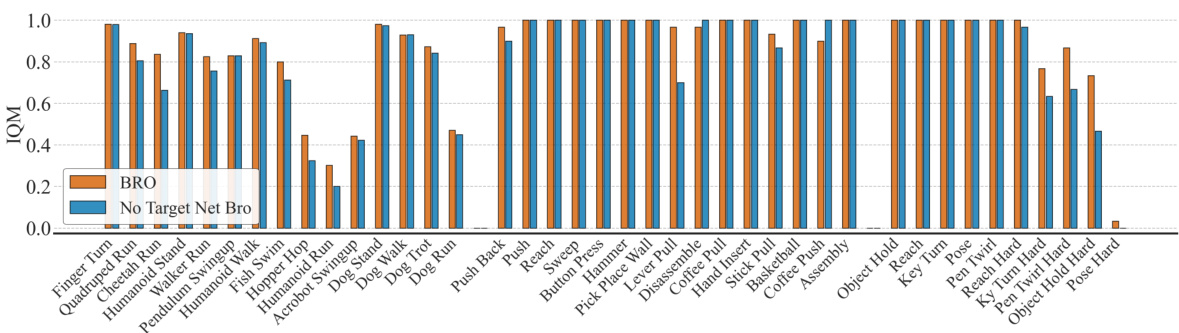
The left plot shows how the impact of several BRO design choices varies depending on the size of the critic network. The choices examined are disabling clipped double Q-learning (+CDQ), reducing the replay ratio (+RR=1), removing full-parameter resets (-Reset), removing the optimistic exploration policy (-Scaled π), removing quantile Q-value approximation (-Quantile), and reducing the batch size (+Batch). The right plot shows the impact of using target networks, comparing results of using target networks to results without them.
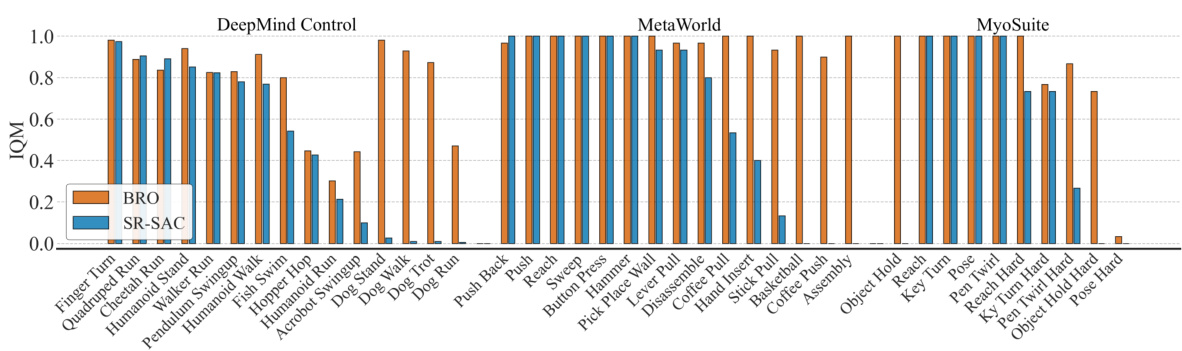
This figure compares the performance of the proposed BRO algorithm against other state-of-the-art model-free and model-based reinforcement learning algorithms across three benchmark suites: DeepMind Control, MetaWorld, and MyoSuite. The BRO algorithm achieves state-of-the-art results, significantly outperforming the other algorithms on 40 complex continuous control tasks. The y-axis represents the interquartile mean performance across 10 random seeds, with 1.0 indicating optimal performance. The results show that BRO is highly sample-efficient, reaching near-optimal performance within 1 million environment steps.
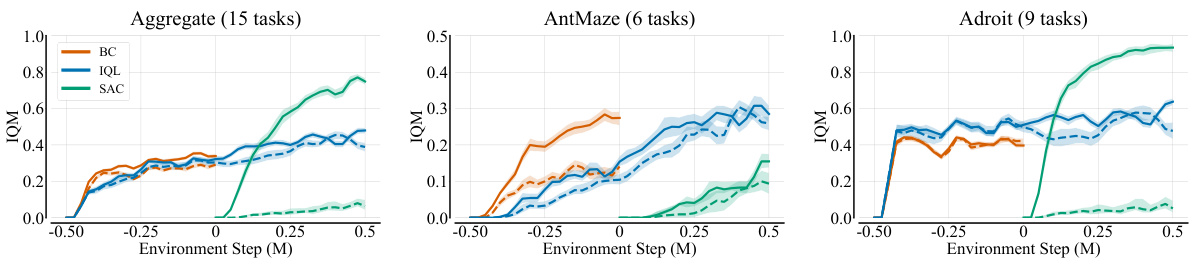
This figure compares the performance of three offline reinforcement learning algorithms (BC, IQL, SAC) with and without the BroNet architecture across three different scenarios: pure offline learning, offline fine-tuning, and online learning with offline data. The BroNet architecture consistently improves performance across all three algorithms and scenarios, demonstrating its broad applicability and effectiveness.
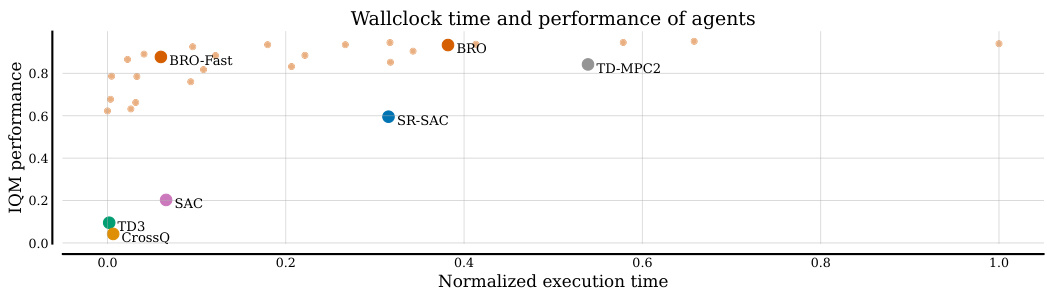
This figure compares the sample efficiency and wall-clock time of the proposed BRO algorithm and its faster variant (BRO-Fast) against several baseline reinforcement learning algorithms across 40 tasks. The left panel shows BRO’s superior sample efficiency, while the right panel demonstrates its faster wall-clock time, especially when compared to a model-based method (TD-MPC2). BRO-Fast achieves similar sample efficiency to TD-MPC2 but with significantly improved performance compared to a standard SAC agent.
This figure compares the performance of different critic network architectures (vanilla dense, spectral normalization ResNet, and BroNet) when used with BRO and SAC algorithms. It shows that increasing the critic’s parameter count leads to performance gains, but only with the right architecture (BroNet) and algorithm (BRO). The plot demonstrates the interplay between architecture, algorithm, and model size in achieving optimal performance. Error bars represent 95% confidence intervals across 10 random seeds.
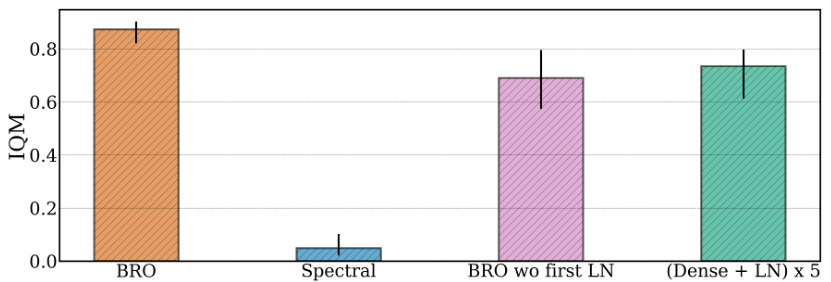
This figure compares the performance of five different network architectures across various continuous control tasks. The architectures tested are BRO, Spectral, BRO without the first Layer Normalization, and a simple 5-layer MLP with Layer Normalization. The results show that BRO outperforms other architectures, particularly on challenging tasks like the Dog Trot environment. This suggests that BRO’s architecture, specifically the use of residual blocks and Layer Normalization, is crucial for achieving good performance on complex continuous control problems.
This figure compares the performance of different critic network architectures (vanilla dense, spectral normalization ResNet, and BroNet) when combined with BRO and SAC algorithms. The x-axis shows the number of parameters in the critic network, and the y-axis represents the average performance across multiple tasks. The results demonstrate that BroNet, combined with BRO, achieves the best performance, highlighting the importance of both architectural design and algorithmic enhancements for optimal scaling.
This figure compares the performance of the proposed BRO algorithm against other state-of-the-art model-free and model-based reinforcement learning algorithms across four benchmark suites (DeepMind Control, MetaWorld, MyoSuite, and Dog & Humanoid). The bar chart shows the interquartile mean performance across 40 different tasks, with 1.0 indicating optimal performance. BRO consistently outperforms other algorithms, demonstrating its effectiveness.
This figure compares the performance of the BRO algorithm against other model-free and model-based algorithms across three benchmark suites: DeepMind Control, MetaWorld, and MyoSuite. Each suite contains multiple tasks, and the graph shows that BRO significantly outperforms other algorithms across all 40 tasks. The Y-axis represents the interquartile mean performance (averaged across 10 random seeds), normalized to 1.0 for optimal performance on each benchmark. The experiment used 1 million environment steps.
This figure presents a bar chart comparing the performance of BRO against other model-free and model-based reinforcement learning algorithms across four benchmark suites: DeepMind Control, MetaWorld, MyoSuite, and Dog & Humanoid. BRO consistently outperforms the other algorithms, achieving state-of-the-art results. The y-axis shows the interquartile mean performance, normalized to 1.0 for optimal performance. The results are averaged over 10 random seeds and are based on 1 million environment steps.
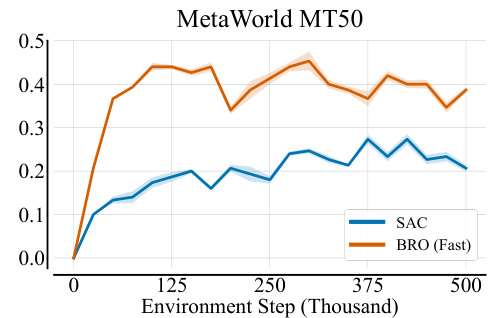
This figure compares the performance of BRO (Fast) and SAC algorithms on the MetaWorld MT50 benchmark. The x-axis represents the number of environment steps (in thousands), and the y-axis shows the interquartile mean (IQM) of the performance. The shaded regions around the lines represent the 95% confidence intervals calculated from 3 random seeds. This comparison highlights the superior performance of BRO (Fast) compared to SAC across the 50 different tasks within the MetaWorld MT50 benchmark.
This figure compares the performance of the proposed BRO algorithm against other state-of-the-art model-free and model-based reinforcement learning algorithms across four benchmark suites (DeepMind Control, MetaWorld, MyoSuite, and Dog and Humanoid). The results are shown as interquartile means across ten random seeds, normalized to the best possible performance (1.0). BRO consistently outperforms other methods across all benchmarks, demonstrating its superior performance. All agents were trained for 1 million environment steps.
This figure compares the performance of BRO against other state-of-the-art model-free and model-based reinforcement learning algorithms across four benchmark suites (DeepMind Control, MetaWorld, MyoSuite, Dog & Humanoid). The results show that BRO significantly outperforms all other algorithms across all 40 tasks, achieving near-optimal performance on the challenging Dog & Humanoid tasks. The y-axis represents the interquartile mean performance, normalized such that 1.0 indicates the best possible performance for each benchmark. The experiment is run for 1 million environment steps.
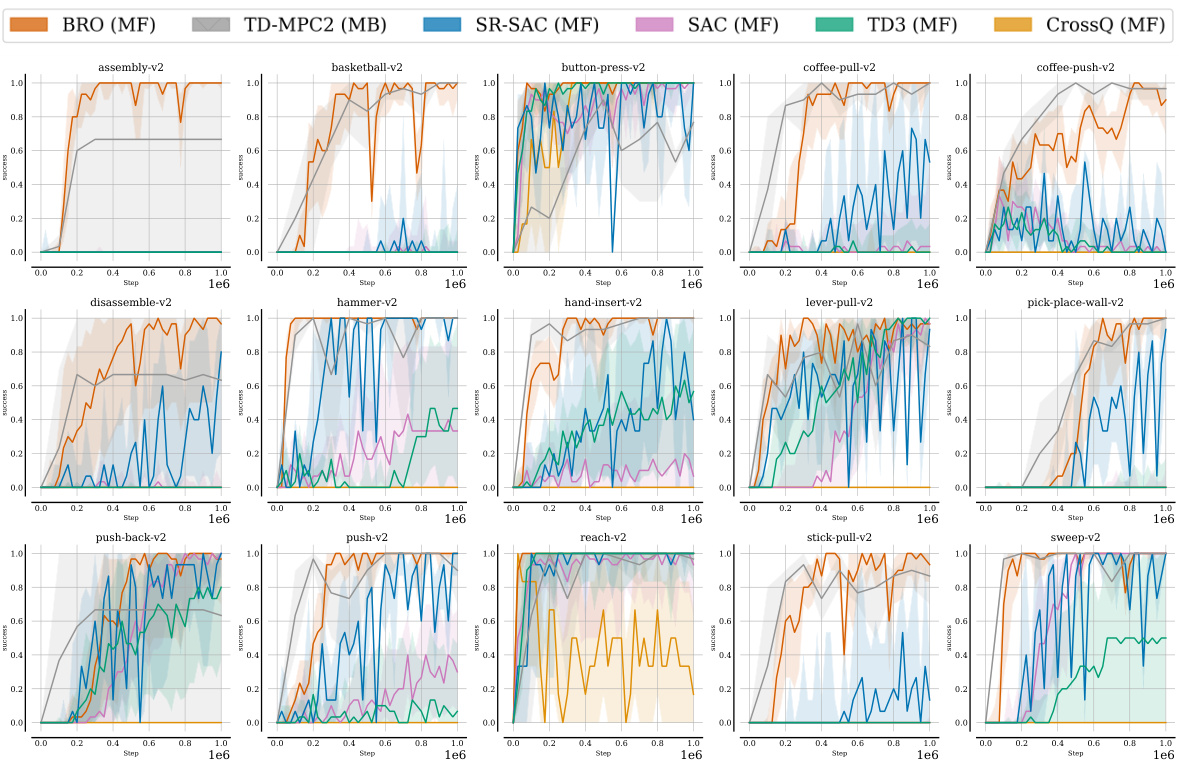
This figure compares the performance of the proposed BRO algorithm against other state-of-the-art model-free and model-based reinforcement learning algorithms across four benchmark suites: DeepMind Control, MetaWorld, MyoSuite, and Dog & Humanoid. The y-axis represents the interquartile mean performance, normalized such that 1.0 is the best possible score for each benchmark. The results show BRO significantly outperforming the other algorithms across all benchmark suites. This demonstrates the effectiveness of the BRO approach in scaling model capacity and achieving sample-efficient continuous control.
This figure compares the performance of the proposed BRO algorithm against other state-of-the-art model-free and model-based reinforcement learning algorithms across four benchmark suites (DeepMind Control, MetaWorld, MyoSuite, and Dog & Humanoid) with a total of 40 tasks. The y-axis represents the interquartile mean performance, normalized to 1.0 (best possible performance), calculated across 10 random seeds. The x-axis represents the benchmark suite and individual tasks within each suite. The results show that BRO significantly outperforms all other algorithms across all benchmarks. Note that these results are obtained using 1 million environment steps.
This figure compares the sample efficiency and wall-clock time of the proposed BRO algorithm (and its faster variant, BRO (Fast)) against several baseline reinforcement learning algorithms across 40 benchmark tasks. The left panel shows BRO achieving superior sample efficiency, while the right panel demonstrates that BRO (Fast) achieves comparable wall-clock time to TD-MPC2 (a model-based method), despite significantly outperforming it in terms of final performance. BRO (Fast) is even faster than a standard SAC agent while still achieving substantially better performance. The results are presented as interquartile means, normalized to the maximum possible performance (1.0).
More on tables
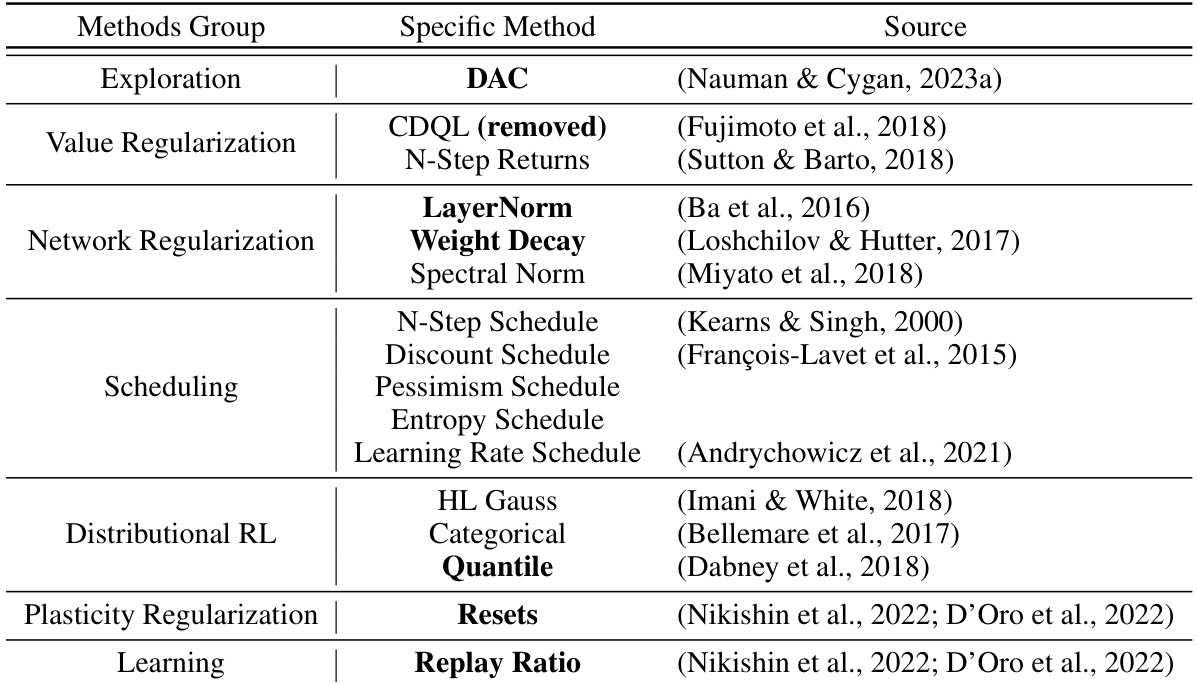
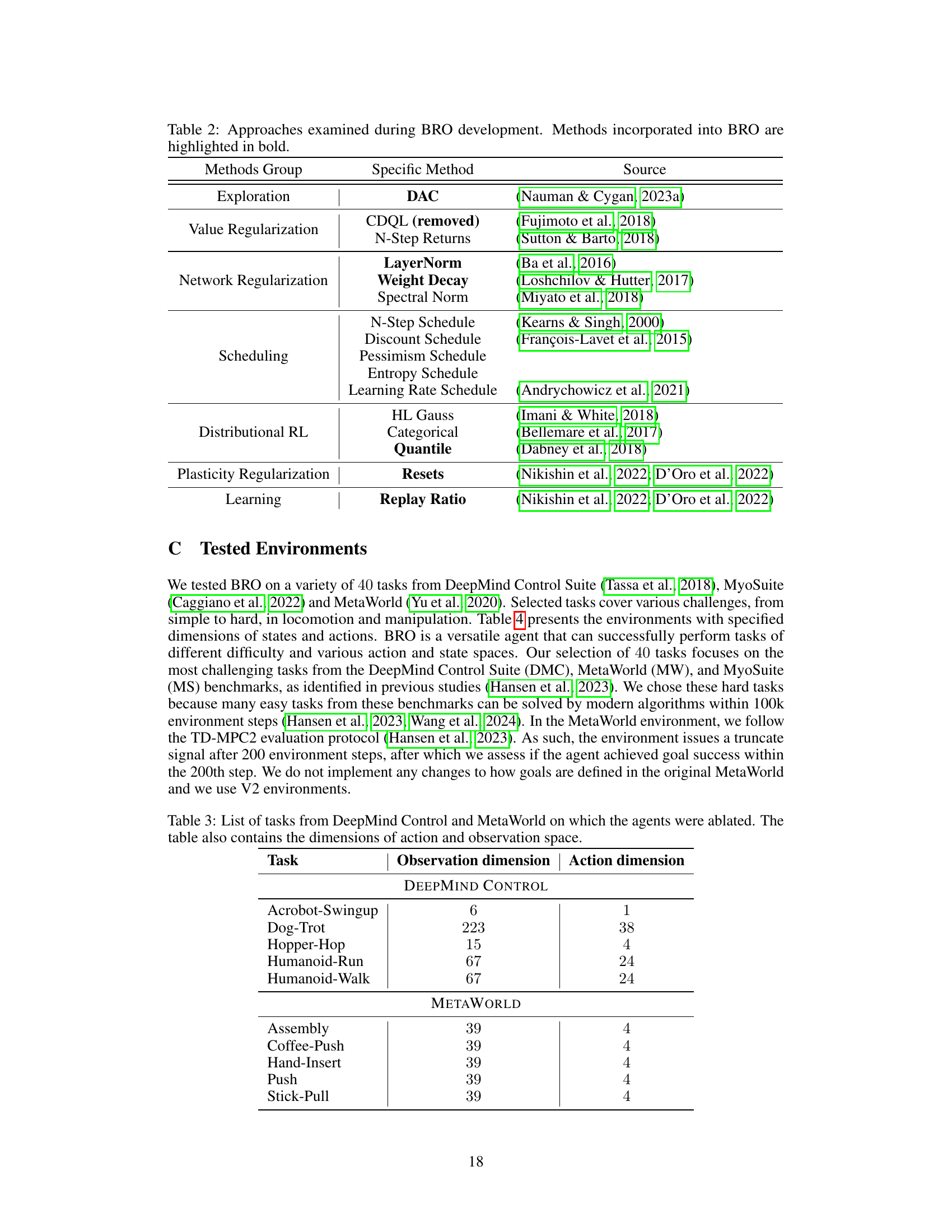
This table summarizes various techniques explored during the development of the BRO algorithm. It categorizes them into groups (Exploration, Value Regularization, Network Regularization, Scheduling, Distributional RL, Plasticity Regularization, Learning) and lists specific methods used within each group, along with their source. The methods highlighted in bold are the ones that were ultimately incorporated into the final BRO algorithm.
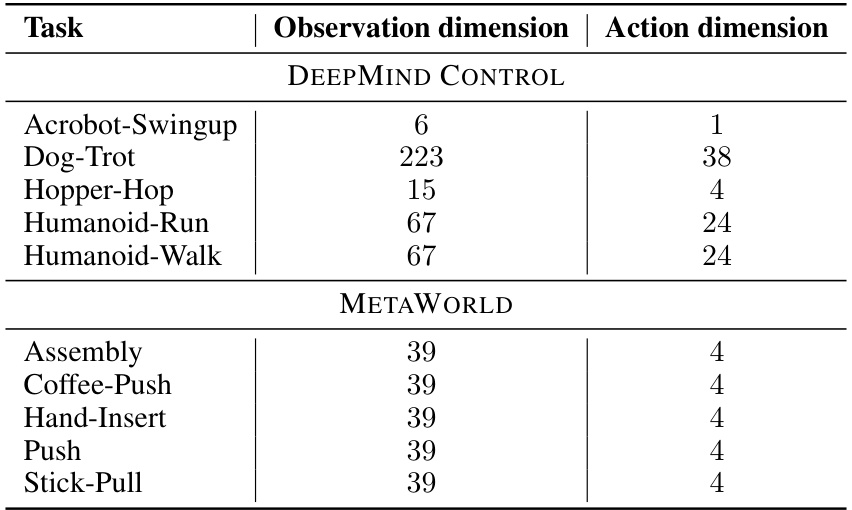
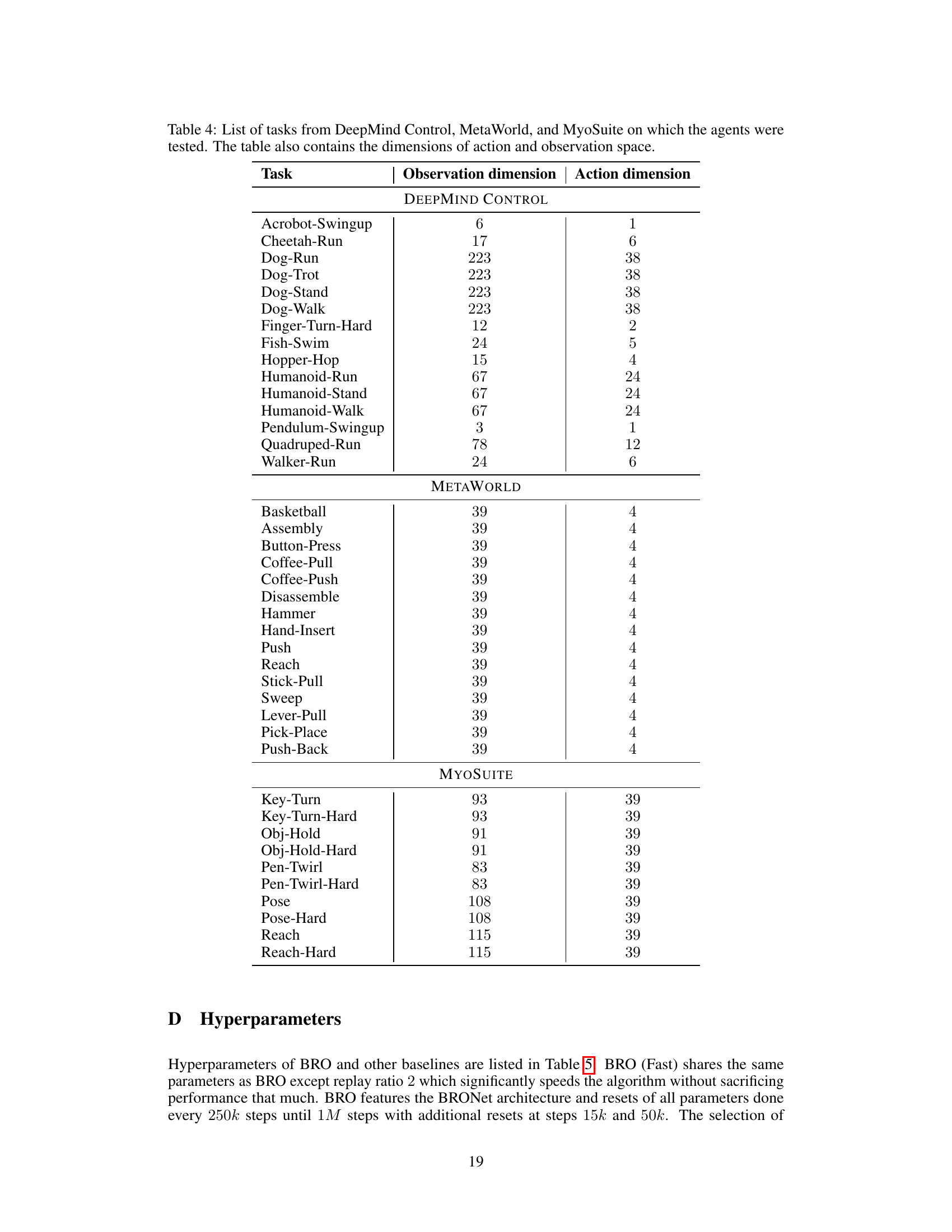
This table lists the 40 tasks used in the paper’s experiments, broken down by benchmark suite (DeepMind Control, MetaWorld, MyoSuite). For each task, the number of dimensions in the observation and action spaces are provided. This information is important for understanding the complexity of the tasks and the computational resources required to solve them.
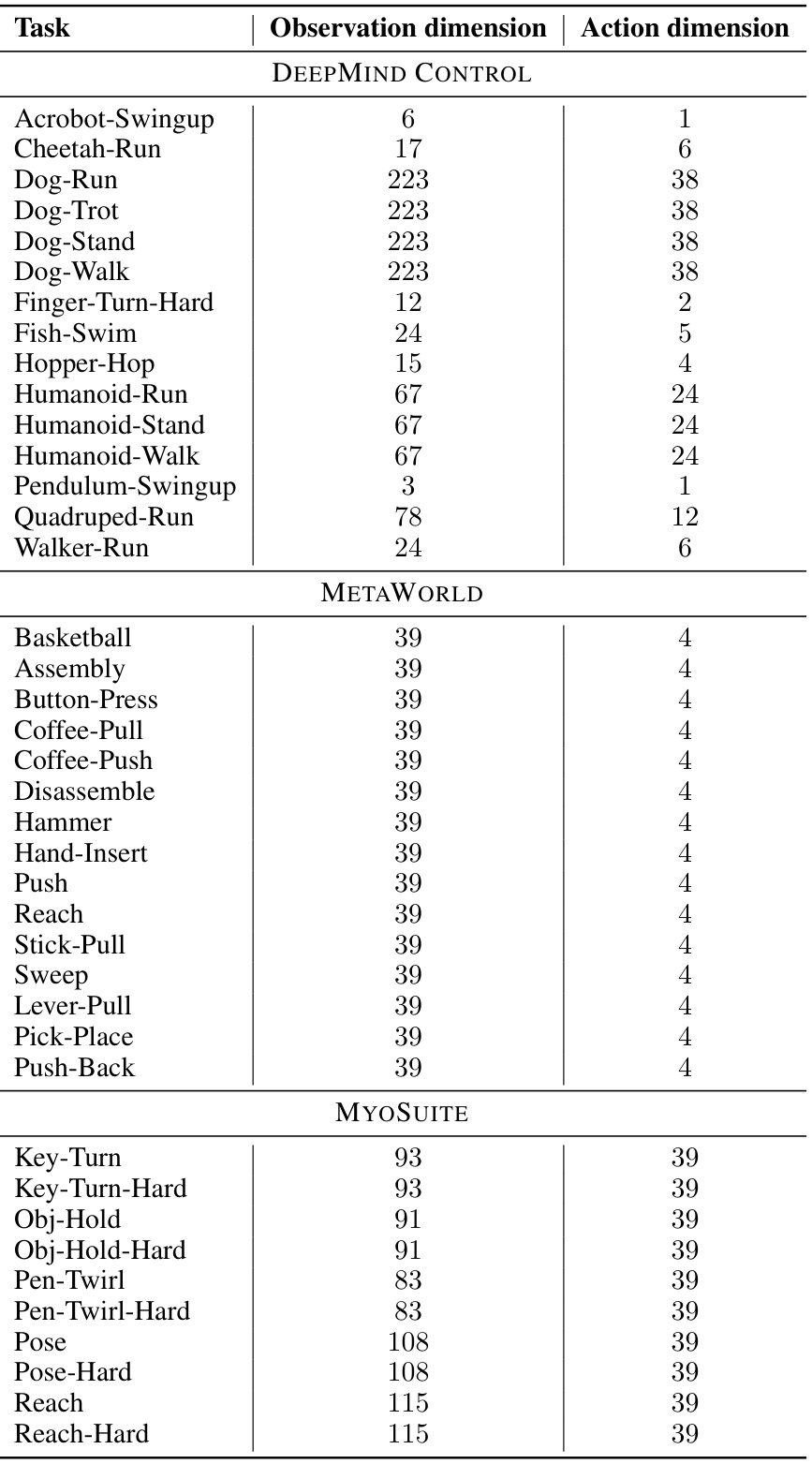
This table lists the 40 continuous control tasks used in the paper’s experiments. These tasks are drawn from three benchmark suites: DeepMind Control, MetaWorld, and MyoSuite. For each task, the table provides the dimensionality of the observation space (number of state variables) and the dimensionality of the action space (number of control signals). This information is crucial for understanding the complexity of each task and for comparing the performance of different reinforcement learning algorithms.
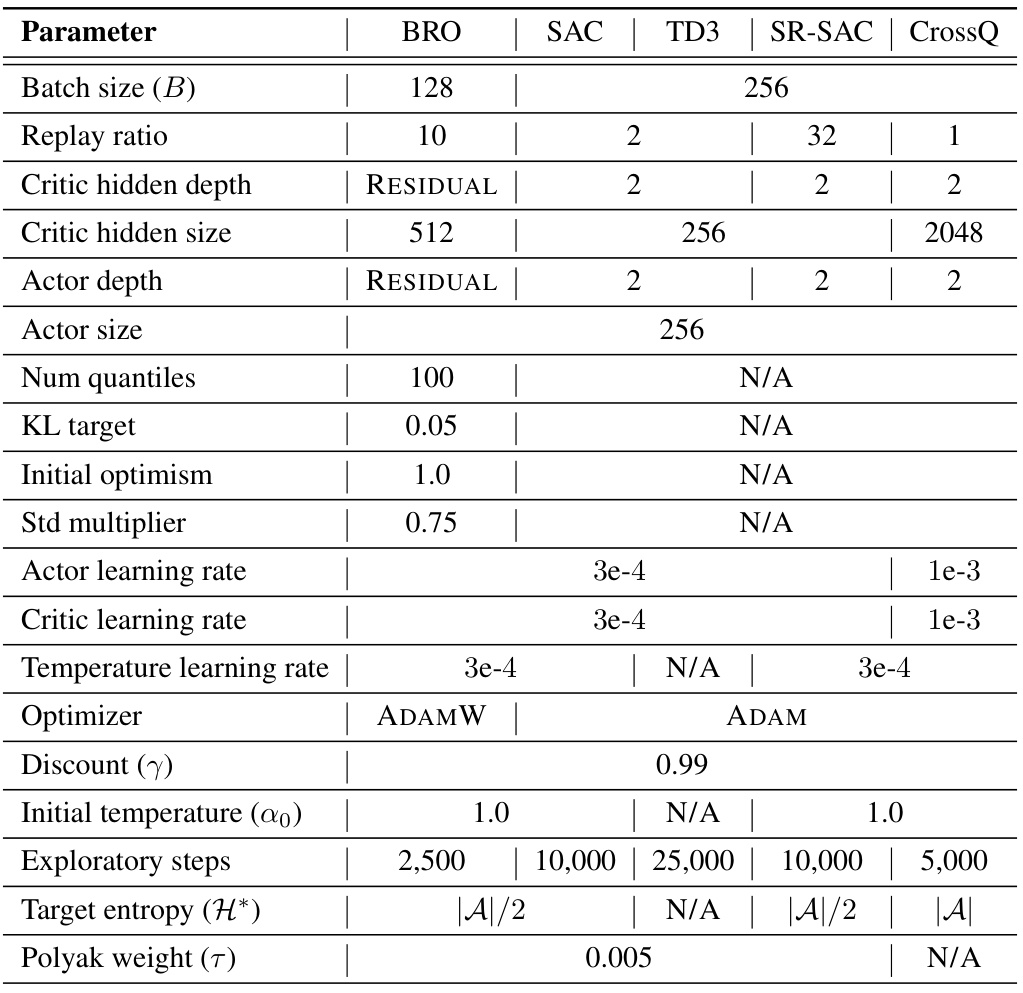
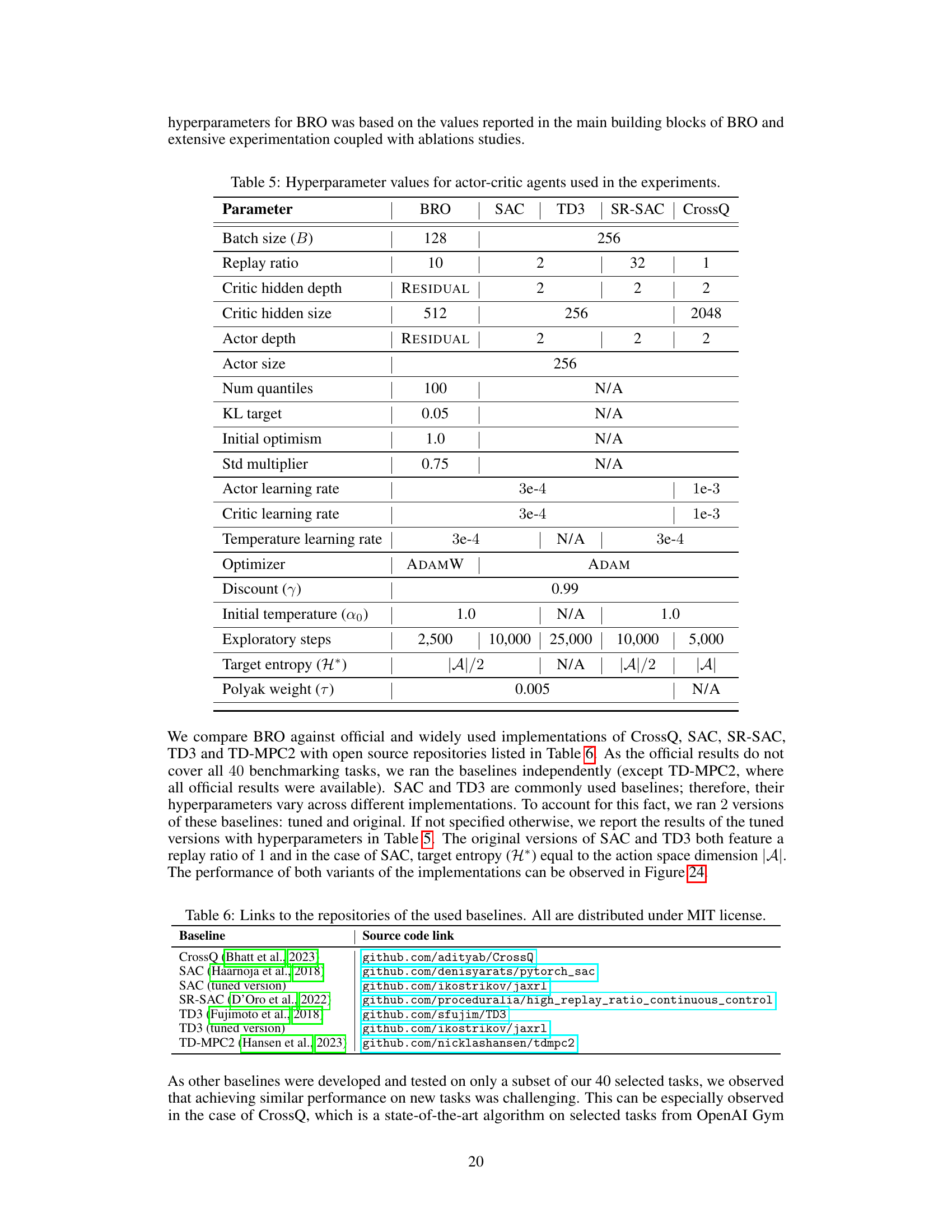
This table lists the hyperparameter settings used for the BRO algorithm and its comparison algorithms (SAC, TD3, SR-SAC, and CrossQ). It details the batch size, replay ratio, critic network architecture and dimensions, actor network dimensions, number of quantiles for quantile regression, KL target for the KL divergence penalty, initial optimism value for optimistic exploration, standard deviation multiplier, learning rates for both actor and critic networks, temperature learning rate, optimizer used, discount factor, initial temperature, number of exploratory steps, target entropy, and Polyak averaging weight. These settings are crucial for replicating the experimental results reported in the paper.

This table provides links to the source code repositories for the various baseline algorithms used in the paper’s experiments. This allows for reproducibility and verification of results. Each algorithm is listed alongside the link to its corresponding repository. All the repositories mentioned are under MIT License.
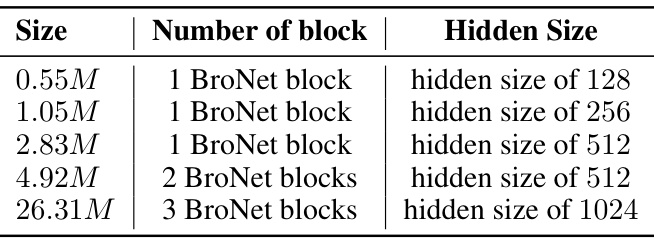
This table describes the different model sizes used in the experiments. Each size is defined by the number of BroNet blocks and the hidden size of each block. The sizes range from 0.55 million parameters to 26.31 million parameters.

This table presents the results of an experiment where the Q-network of the SR-SPR algorithm (a sample-efficient SAC implementation) was replaced with the BroNet architecture. The experiment tested two different reset interval (RI) values and shrink-and-perturb (SP) values to investigate their impact on performance. The results are presented for three Atari games: Pong, Seaquest, and Breakout.
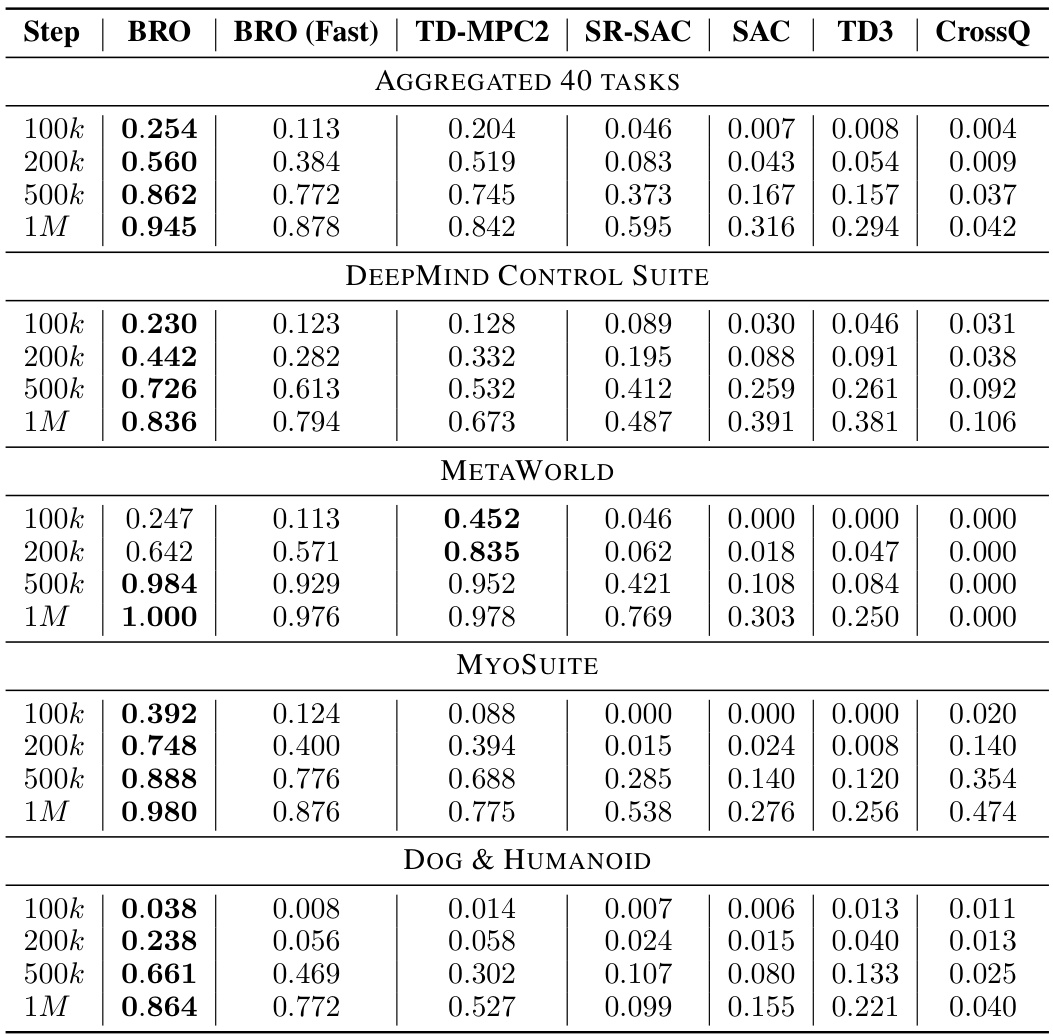
This table presents a summary of the Interquartile Mean (IQM) performance results for BRO and several other baseline algorithms across 40 continuous control tasks from three benchmark suites (DeepMind Control, MetaWorld, and MyoSuite). The results are shown at four different stages of training: 100k, 200k, 500k, and 1M environment steps. The table is organized to show the performance across the aggregated tasks as well as broken down by benchmark suite, providing a comprehensive view of the BRO algorithm’s performance in various scenarios and in comparison to other leading methods.
Full paper#