↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Automatic differentiation (AD) is crucial for computing gradients and Jacobians across many fields, but existing methods often trade computational efficiency for approximations. This paper tackles the challenge of optimizing Jacobian computation for exact results while minimizing computational cost, a known NP-hard problem. Current methods such as forward and reverse-mode AD, or minimal Markowitz degree, offer only limited efficiency gains.
The proposed AlphaGrad approach addresses this by framing Jacobian computation as a game played by a deep reinforcement learning (RL) agent, called VertexGame. This agent learns to find the optimal vertex elimination order in a computational graph, reducing the number of necessary multiplications. The approach is validated on diverse tasks, demonstrating significant improvements (up to 33%) over existing methods. Furthermore, a new AD interpreter in JAX, called Graphax, is developed to execute the obtained optimal orders, translating theoretical gains into actual runtime improvements.
Key Takeaways#
Why does it matter?#
This paper is highly important as it presents AlphaGrad, a novel method for optimizing automatic differentiation (AD) using deep reinforcement learning. This significantly improves the efficiency of Jacobian computations, impacting various scientific domains. It also introduces Graphax, a new JAX-based AD package that translates the theoretical gains into practical runtime improvements. The research opens exciting new avenues for AD algorithm discovery, potentially revolutionizing scientific computing in many areas.
Visual Insights#
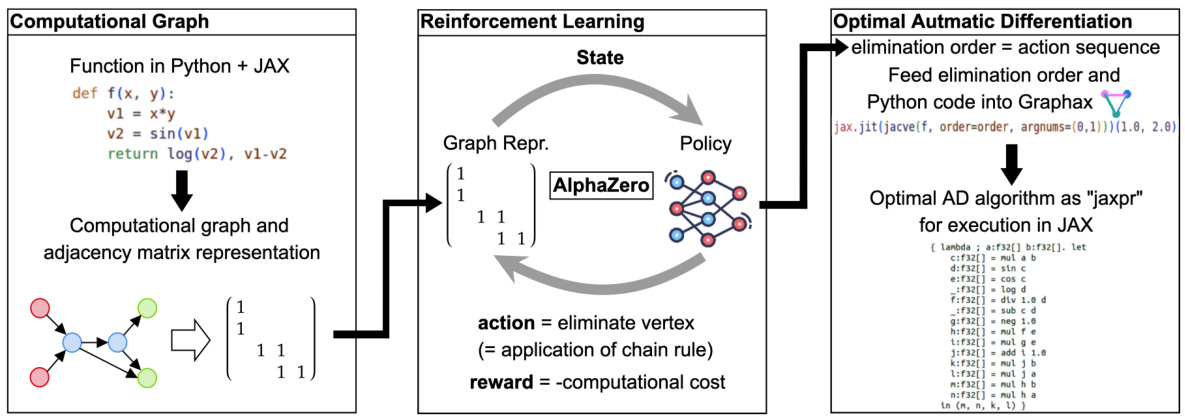
This figure illustrates the AlphaGrad pipeline, which uses deep reinforcement learning to discover new automatic differentiation (AD) algorithms. It starts with a function defined in Python and JAX, which is then converted into a computational graph representation and an adjacency matrix. This representation serves as input to the AlphaZero-based reinforcement learning agent, which selects actions (eliminating vertices in the graph) to minimize the computational cost. The resulting optimal elimination order, along with the original Python code, is then fed into the Graphax interpreter (a JAX-based AD package), producing an optimal AD algorithm in the form of a JAX ‘jaxpr’ for efficient execution. This workflow leads to AD algorithms that show significant improvements over existing state-of-the-art methods.
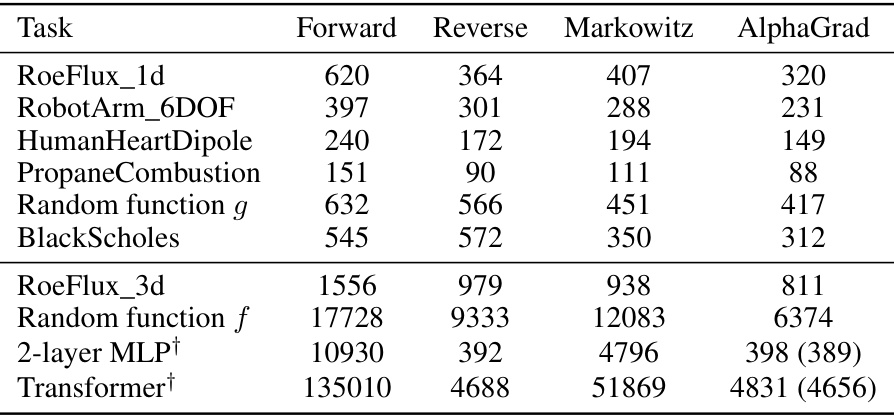
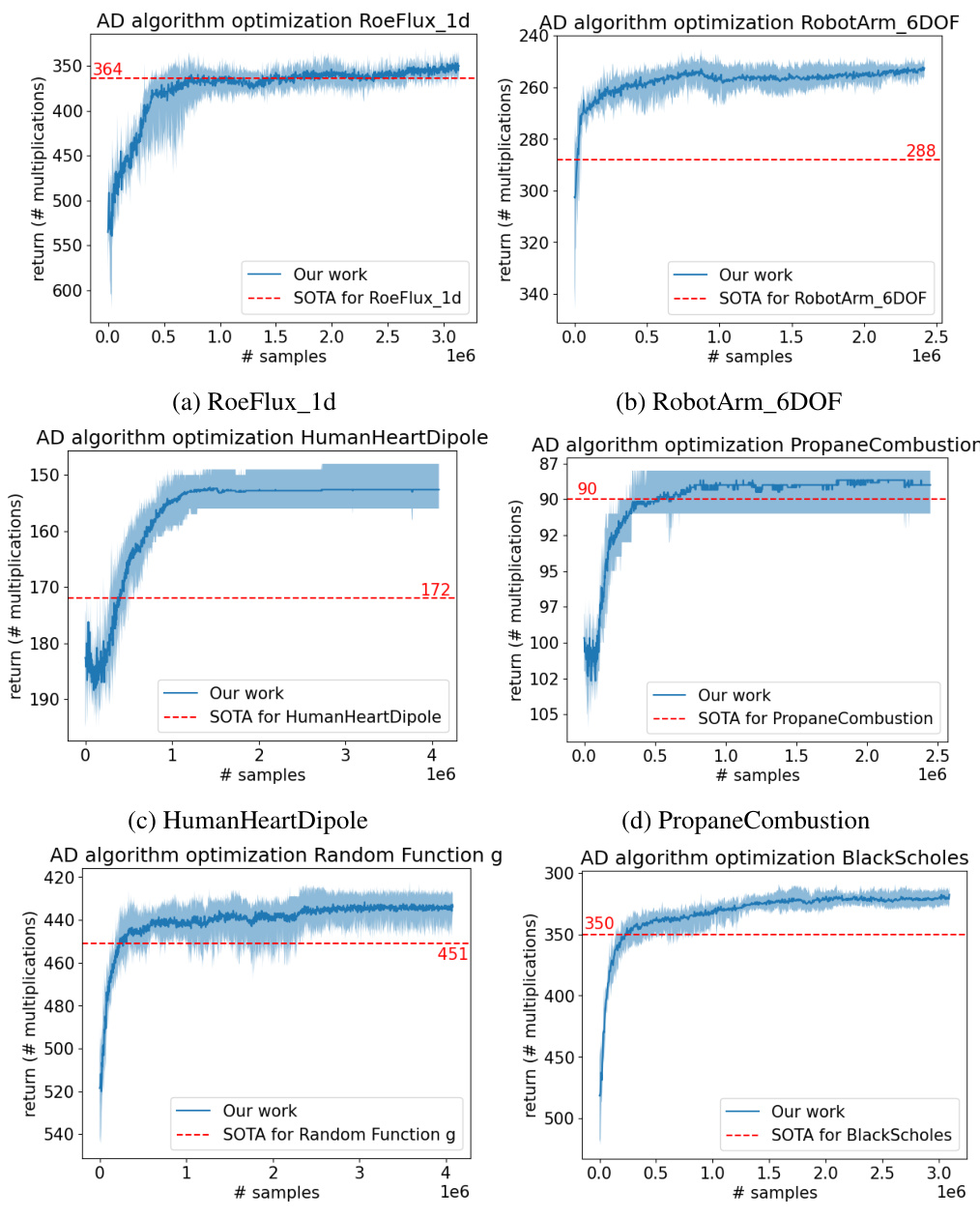
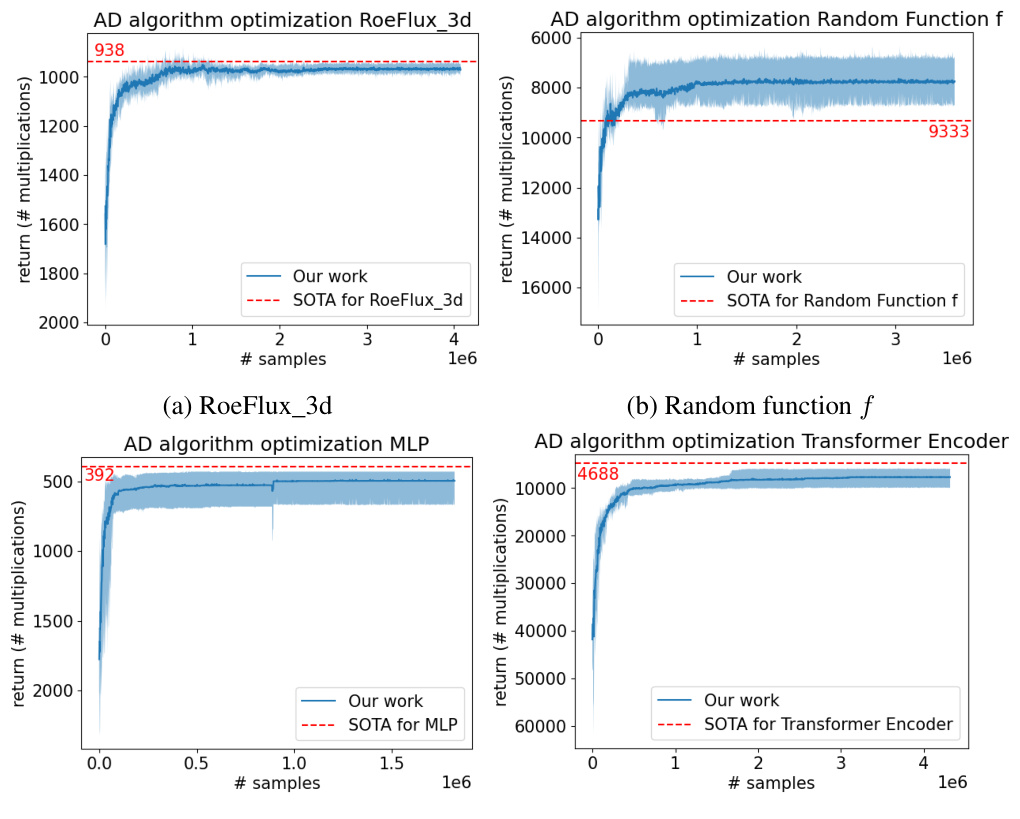
This table presents the number of multiplications needed for Jacobian computation using different methods, including forward mode, reverse mode, the minimal Markowitz degree method, and AlphaGrad. AlphaGrad significantly outperforms other methods in most cases. The table also indicates the use of a log-scaling for some experiments.
In-depth insights#
AlphaGrad: RL for AD#
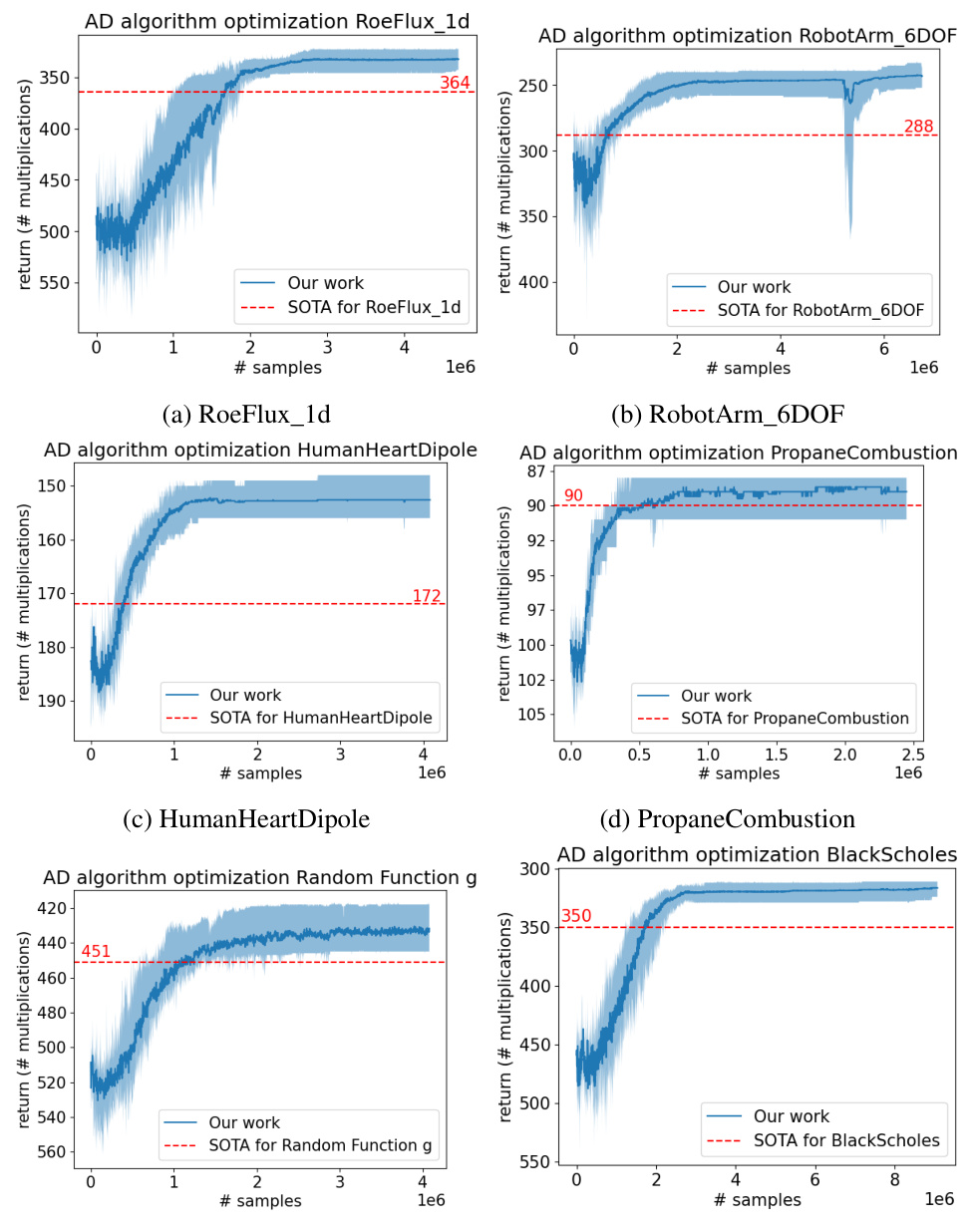
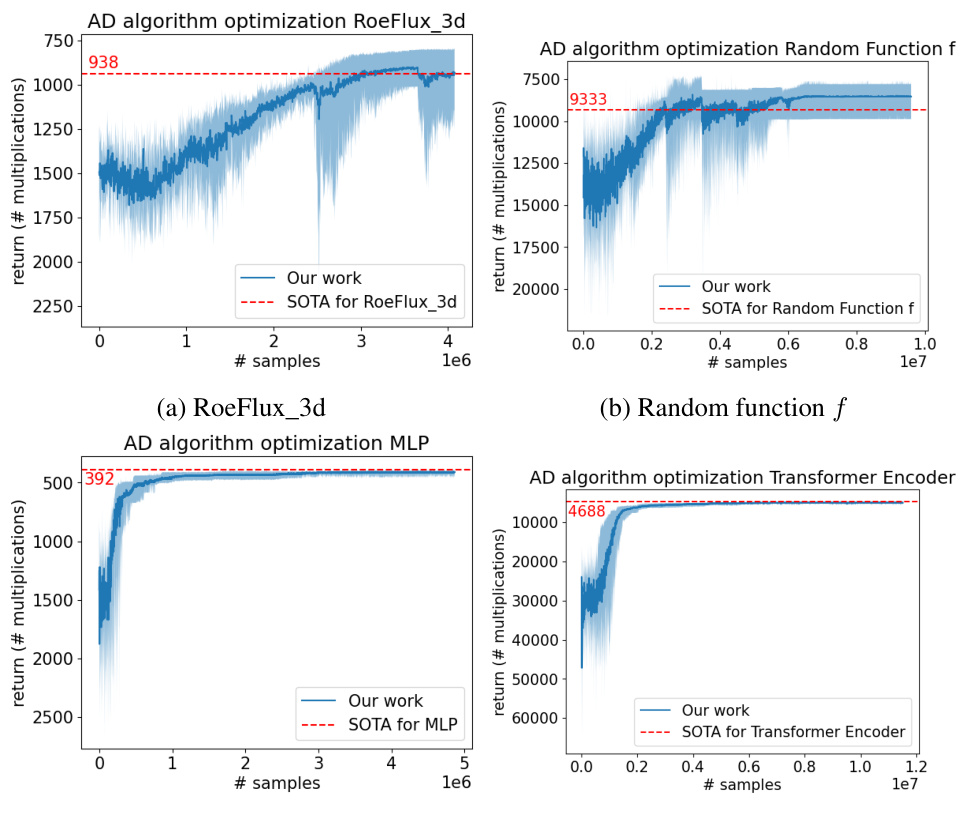
AlphaGrad leverages reinforcement learning (RL) to optimize automatic differentiation (AD), specifically focusing on minimizing the computational cost of Jacobian calculations. The core innovation is framing Jacobian computation as a game, the VertexGame, where an RL agent learns to find the optimal order for eliminating vertices in the computational graph. This strategy, unlike existing AD methods, achieves exact Jacobian computation without sacrificing efficiency. By training a neural network via deep RL, AlphaGrad discovers novel AD algorithms surpassing the performance of state-of-the-art techniques. The theoretical improvements translate into practical runtime speedups, as demonstrated by the authors’ implementation, Graphax, a JAX-based AD interpreter that can efficiently execute these algorithms. AlphaGrad’s effectiveness spans diverse domains, including deep learning, computational fluid dynamics, and robotics, making it a promising approach for enhancing the performance of AD across various scientific and engineering applications. However, a limitation is the requirement of static computational graphs, hindering the use of dynamic control flow present in many real-world applications.
Cross-Country Elim#
Cross-country elimination (CCE) is a novel method for optimizing automatic differentiation (AD) by rephrasing Jacobian computation as an ordered vertex elimination problem on a computational graph. Each elimination step incurs a computational cost, and the goal is to find an optimal elimination sequence minimizing the total cost. This approach leverages deep reinforcement learning (RL) to discover efficient elimination orders, surpassing traditional methods like forward and reverse mode AD, as well as minimal Markowitz degree. The RL agent learns to play a game, selecting vertices for elimination based on minimizing the number of required multiplications. This technique avoids approximation of the Jacobian, ensuring accuracy while enhancing computational efficiency. Experimental results demonstrate up to 33% improvements over existing methods across various scientific domains. The method’s effectiveness is further validated by translating the discovered elimination orders into actual runtime improvements using a custom JAX interpreter, Graphax, highlighting the practical applicability and significant potential of CCE.
Graphax: JAX AD#
The heading “Graphax: JAX AD” suggests a novel automatic differentiation (AD) library built using JAX. Graphax leverages the computational graph representation of functions, likely offering improvements over existing JAX AD implementations. The integration with JAX is a key feature, as JAX provides efficient just-in-time (JIT) compilation and automatic vectorization, leading to potential performance gains. A core functionality of Graphax is likely cross-country elimination, a technique for computing Jacobians by eliminating vertices in a specific order on the computational graph. This approach potentially yields computational advantages compared to standard forward or reverse-mode AD. The effectiveness of Graphax likely depends on the choice of vertex elimination order, which could be determined heuristically or using optimization techniques. The implication is that Graphax provides a flexible and potentially more efficient tool for computing gradients and Jacobians in machine learning, computational fluid dynamics, and other domains that depend heavily on AD.
Runtime Improve#
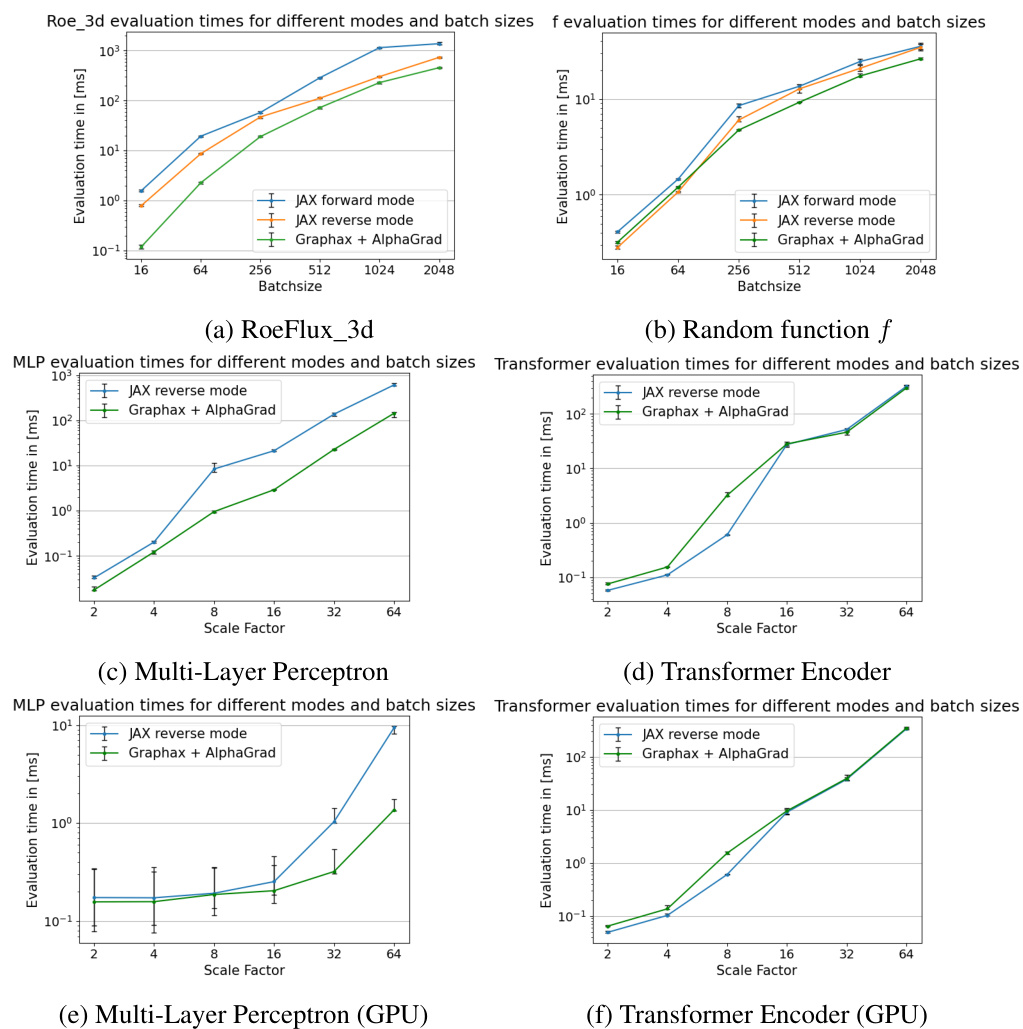
The runtime improvements section of this research paper is crucial because it bridges the gap between theoretical gains and practical applications. The authors cleverly address this by presenting Graphax, a novel sparse automatic differentiation (AD) interpreter built using JAX. This is significant because Graphax allows the execution of the optimized elimination orders discovered by their deep reinforcement learning (RL) model, AlphaGrad. The empirical results demonstrate that Graphax significantly outperforms existing AD implementations on several real-world tasks, especially when dealing with large batch sizes. The key strength is the combination of AlphaGrad’s optimized algorithms and Graphax’s efficient execution capabilities. This showcases not just theoretical advantages, but also tangible speedups in computation, confirming the value and practical relevance of the RL-based approach to AD optimization.
Future Research#
Future research directions stemming from this work on optimizing automatic differentiation (AD) with deep reinforcement learning could focus on several key areas. Extending the approach to handle dynamic computational graphs that involve control flow is crucial for broader applicability. Current limitations restrict the method to static graphs, limiting its use in many real-world scenarios. Another important direction involves developing more general and robust reward functions. The current method relies heavily on the number of multiplications, which is a proxy for runtime and not always perfectly correlated. Exploring other metrics or designing more sophisticated reward functions that directly consider execution time and memory usage could lead to even more efficient AD algorithms. Furthermore, investigating different reinforcement learning algorithms beyond AlphaZero is important. While AlphaZero demonstrated impressive results, other algorithms like PPO might offer advantages in terms of training efficiency or scalability. Finally, exploring hardware-specific optimizations could significantly enhance performance. Tailoring AD algorithms to specific hardware architectures, such as GPUs and specialized accelerators, could lead to significant improvements in computational efficiency. Addressing the problem of the NP-completeness of optimal AD algorithm search, perhaps using advanced approximation methods, also presents a significant challenge for future work.
More visual insights#
More on figures
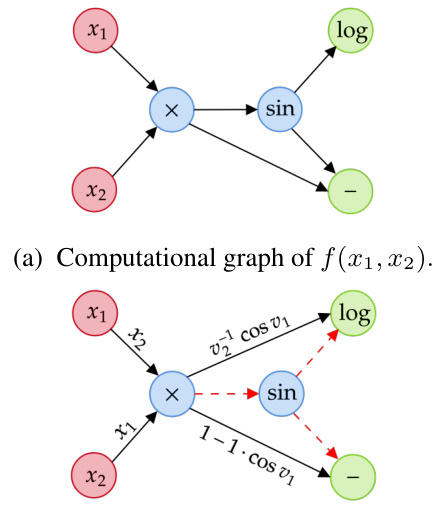
This figure demonstrates the step-by-step process of cross-country elimination using a simple example function. It shows how partial derivatives are added to the edges, how vertices are eliminated (using the chain rule), and how the final bipartite graph contains the Jacobian entries.
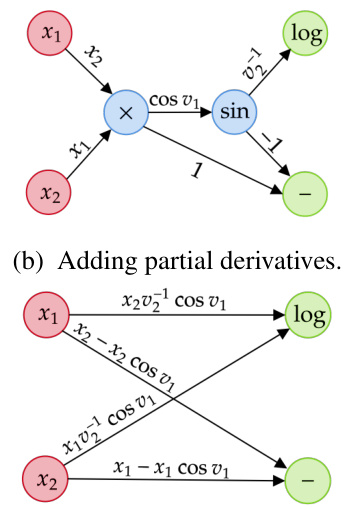
This figure shows a step-by-step illustration of the cross-country elimination algorithm applied to a simple example function. It demonstrates how partial derivatives are added to the edges of the computational graph (b), a vertex is eliminated (c), and the process continues until a final bipartite graph is obtained (d), where the edges represent the Jacobian.

This figure shows how Graphax implements sparse vertex elimination (a) and the three-dimensional adjacency tensor used to represent the computational graph (b). The tensor encodes the shape and sparsity of Jacobians, and its vertical slices are fed into a transformer network.
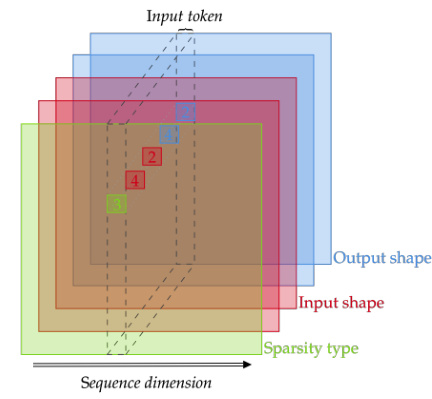
This figure shows how Graphax (a novel sparse AD package) benefits from sparse vertex elimination in cross-country elimination. Panel (a) illustrates the sparse elimination process; (b) displays the 3D adjacency tensor used to represent the computational graph. This tensor encodes 5 aspects of each edge: input/output shape and sparsity type of the associated Jacobian. These vertical slices, representing a single vertex’s input connectivity, are compressed and input to the transformer network as tokens, creating a sequence processed by the model.
This figure shows how Graphax leverages sparse vertex elimination for efficiency and the three-dimensional adjacency tensor used to represent the computational graph for the reinforcement learning model. The tensor encodes information about the shape and sparsity of Jacobians, enabling efficient processing by the transformer network.
This figure shows how Graphax leverages sparse matrix multiplication for efficient cross-country elimination. Panel (a) illustrates the concept of sparse vertex elimination, highlighting its efficiency compared to dense methods. Panel (b) details the 3D tensor representation of the computational graph used by the reinforcement learning agent, where each dimension encodes information about the graph structure (adjacency), Jacobian shape, and sparsity. The visualization helps explain how the graph is processed by the transformer network in the AlphaGrad pipeline.
This figure shows how Graphax leverages sparse vertex elimination for efficiency and illustrates the three-dimensional adjacency tensor used to represent the computational graph in the reinforcement learning model. The tensor encodes information about the shape and sparsity of Jacobians, which are then processed by a transformer network.
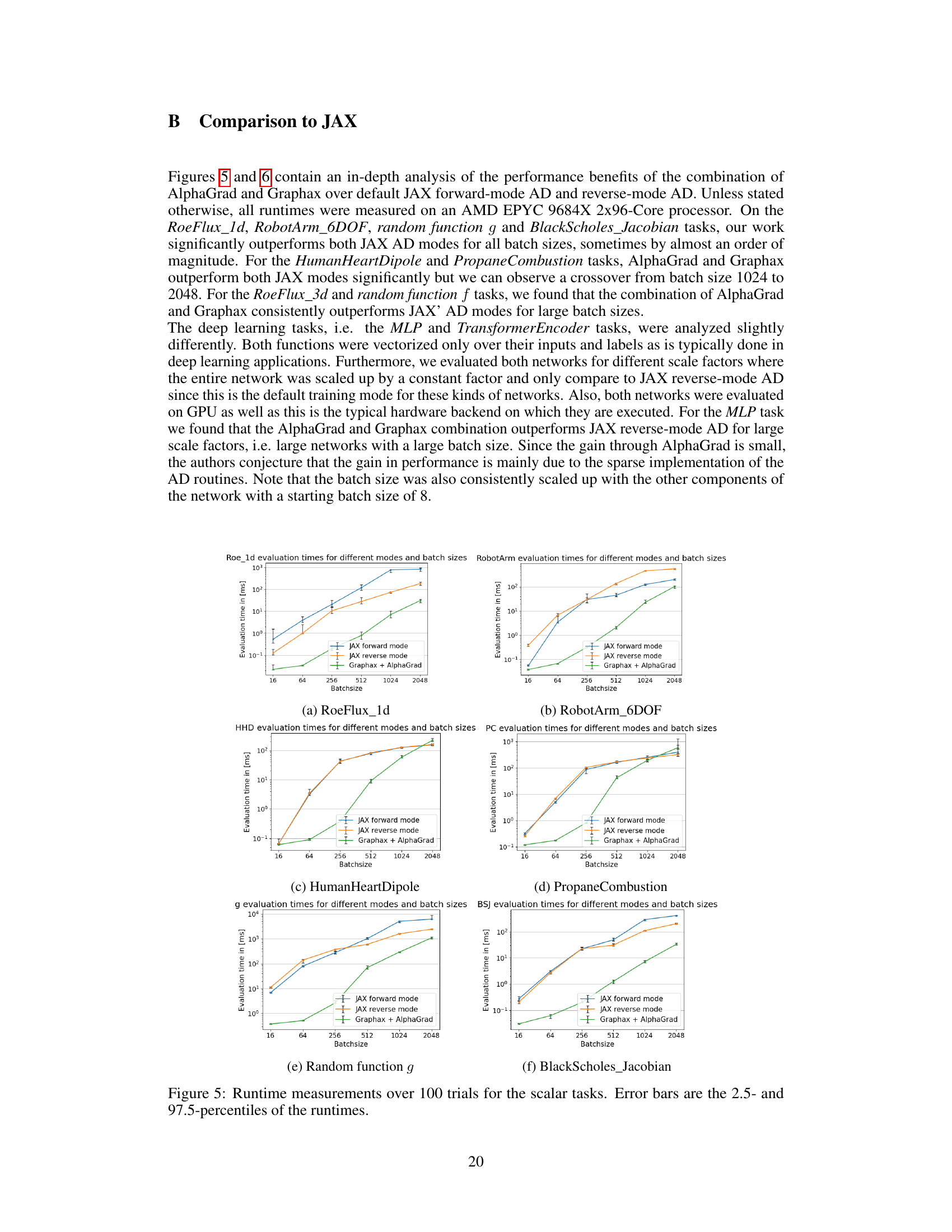
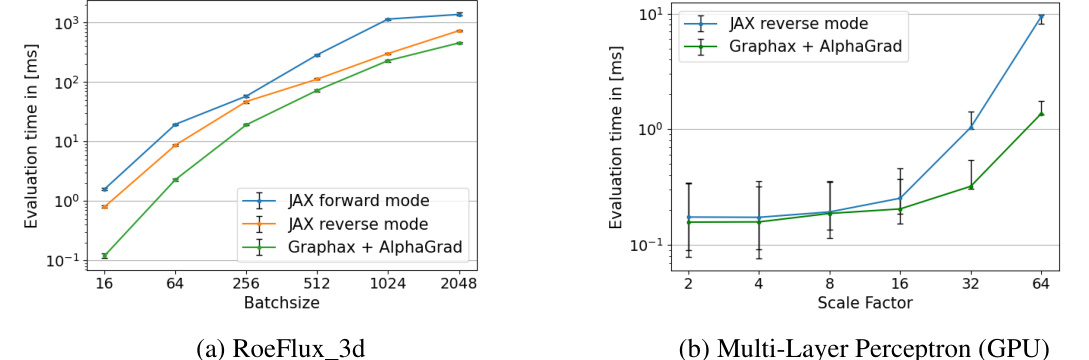
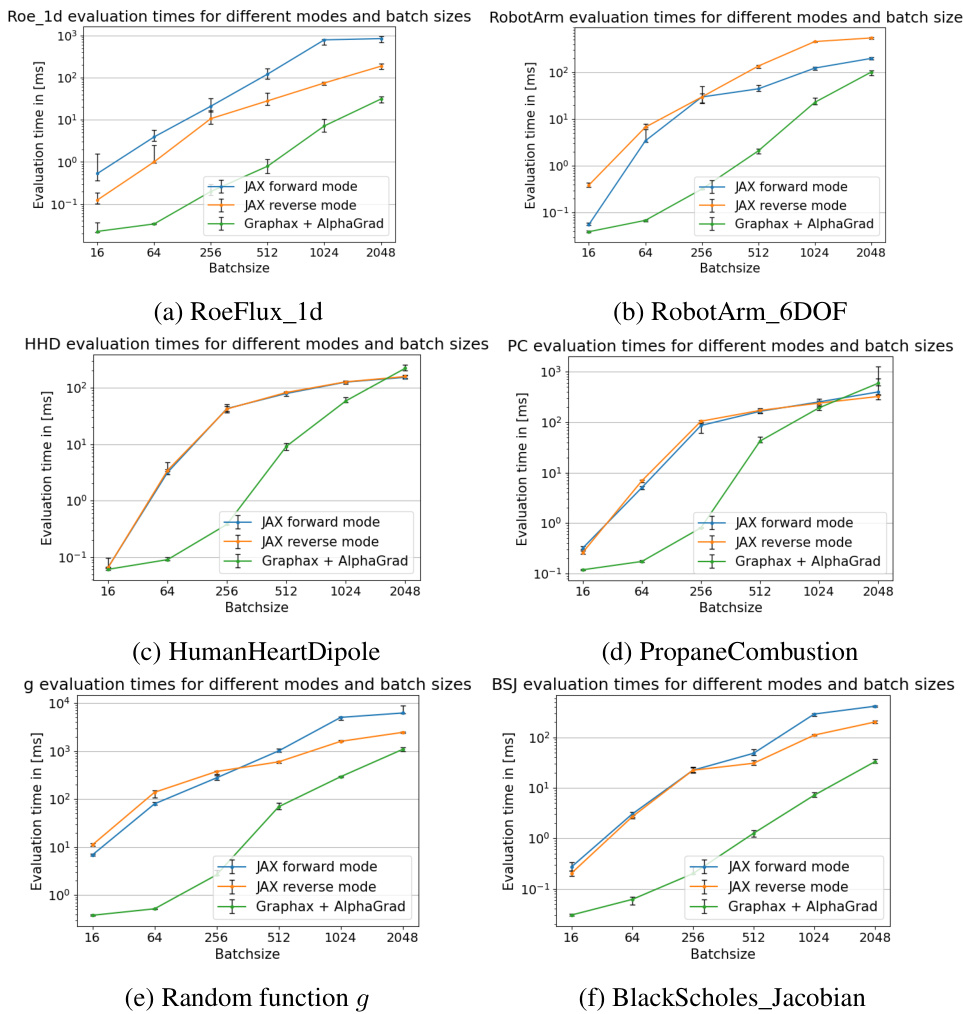
This figure presents the runtime measurements obtained for six different scalar tasks across various batch sizes. The performance of AlphaGrad and Graphax is compared against JAX’s forward and reverse-mode AD. Error bars represent the 2.5th and 97.5th percentiles of the runtime across 100 trials. The results illustrate the efficiency gains achieved by AlphaGrad and Graphax, particularly at larger batch sizes.
This figure shows how Graphax leverages sparse vertex elimination for efficiency and illustrates the three-dimensional adjacency tensor used to represent the computational graph in the AlphaGrad algorithm. The tensor encodes information about the shape and sparsity of Jacobians associated with each edge in the graph, allowing the algorithm to optimize the elimination order effectively.
This figure shows how Graphax leverages sparse vertex elimination for efficiency and illustrates the 3D adjacency tensor used to represent the computational graph in the AlphaGrad RL system. The tensor encodes the shapes and sparsity of Jacobians, which are fed as tokens into a transformer network.
This figure shows how Graphax leverages sparse matrix multiplications for efficient computation of Jacobians using cross-country elimination. Panel (a) illustrates the concept of sparse vertex elimination in Graphax, contrasting it with the standard method. Panel (b) details the three-dimensional tensor representation used to encode the computational graph’s structure, Jacobian shapes, and sparsity information. Each dimension within this tensor holds specific information about the graph and facilitates efficient processing by the deep reinforcement learning model.
This figure shows how Graphax, a novel sparse AD package, implements sparse vertex elimination. Panel (a) illustrates the process by highlighting the advantages of element-wise multiplication instead of matrix multiplication. Panel (b) details the three-dimensional adjacency tensor used to represent the computational graph. The tensor encodes the shape and sparsity of the Jacobians, with each vertical slice representing the input connectivity of a single vertex. These slices are compressed into tokens that are fed into a transformer for processing.
This figure shows how Graphax implements sparse vertex elimination and the three-dimensional adjacency tensor used to represent the computational graph in the RL algorithm. The adjacency tensor encodes information about the shapes and sparsity of the Jacobians associated with each edge in the graph. These are compressed and fed into a transformer for processing.
More on tables
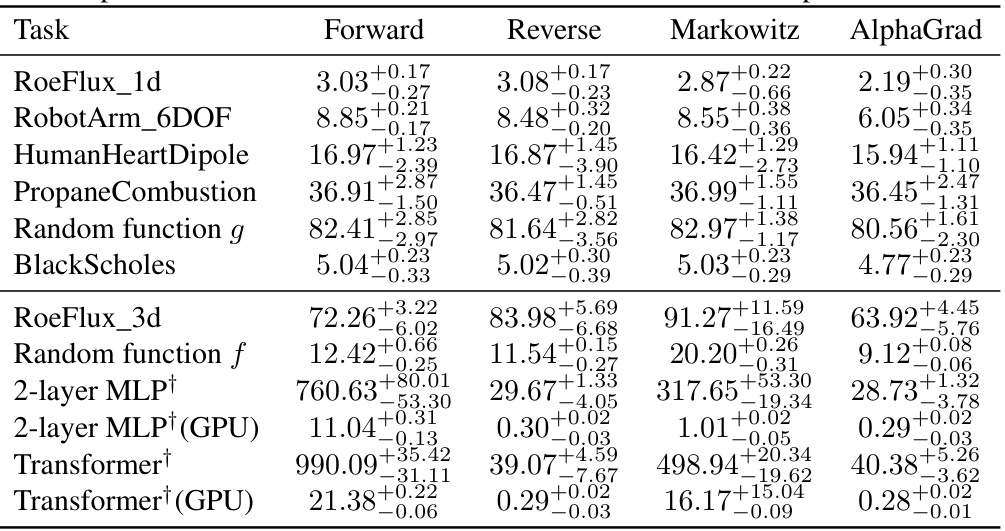
This table presents the number of multiplications needed for Jacobian computation using different methods: forward mode, reverse mode, Markowitz, and AlphaGrad. The AlphaGrad results represent the best elimination order found by the AlphaZero agent in the VertexGame. The table compares the number of multiplications required by AlphaGrad to the baseline methods for various tasks spanning different domains, including computational fluid dynamics and deep learning. The use of a log-scaling for cumulative rewards is also noted, along with the number of Monte Carlo Tree Search (MCTS) simulations used.

This table presents the number of multiplications required by the best elimination order discovered by the AlphaZero agent for different tasks. It compares the results of the proposed AlphaGrad method to baselines including forward-mode AD, reverse-mode AD, and minimal Markowitz degree. The table also notes the use of a log-scaled cumulative reward in some experiments, and provides results for both 50 and 250 Monte Carlo Tree Search simulations.

This table presents the number of multiplications needed for Jacobian computation using different methods. It compares the performance of AlphaGrad (a novel method using deep reinforcement learning) against baseline methods such as forward-mode, reverse-mode, and minimal Markowitz degree. The table shows the number of multiplications for each method across various tasks from different domains. The results demonstrate AlphaGrad’s effectiveness in minimizing the number of multiplications needed, leading to potential improvements in computational efficiency and runtime. The table also indicates the use of different reward scaling techniques in some experiments.

This table presents the number of multiplications needed for Jacobian computation using different methods for various tasks. It compares the performance of the AlphaGrad method (using deep reinforcement learning) against baseline methods like forward-mode AD, reverse-mode AD, and minimal Markowitz degree. The table shows the number of multiplications for each method and highlights the improvement achieved by AlphaGrad. The table also indicates tasks where a log-scaling of the cumulative reward was used during training.

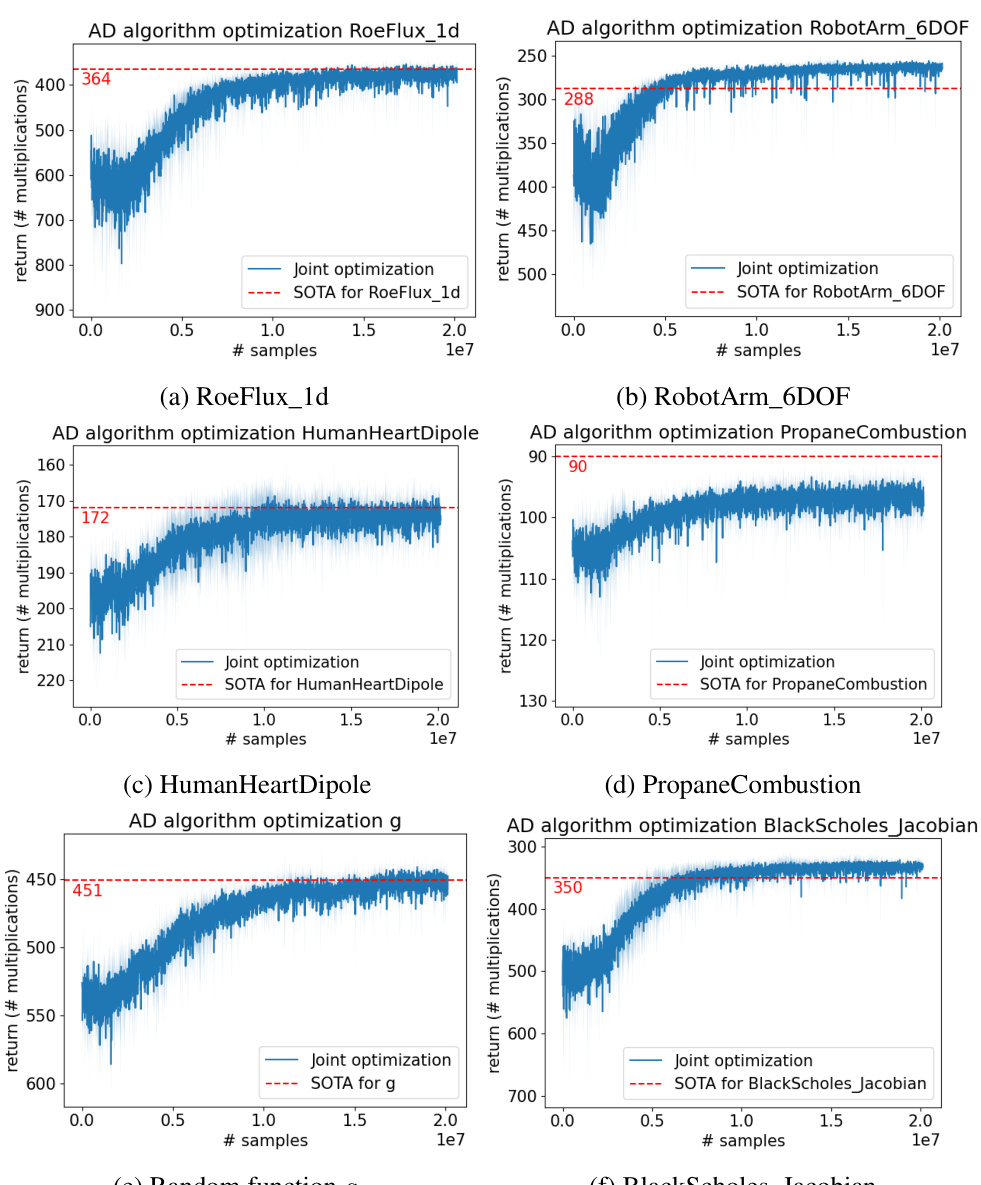
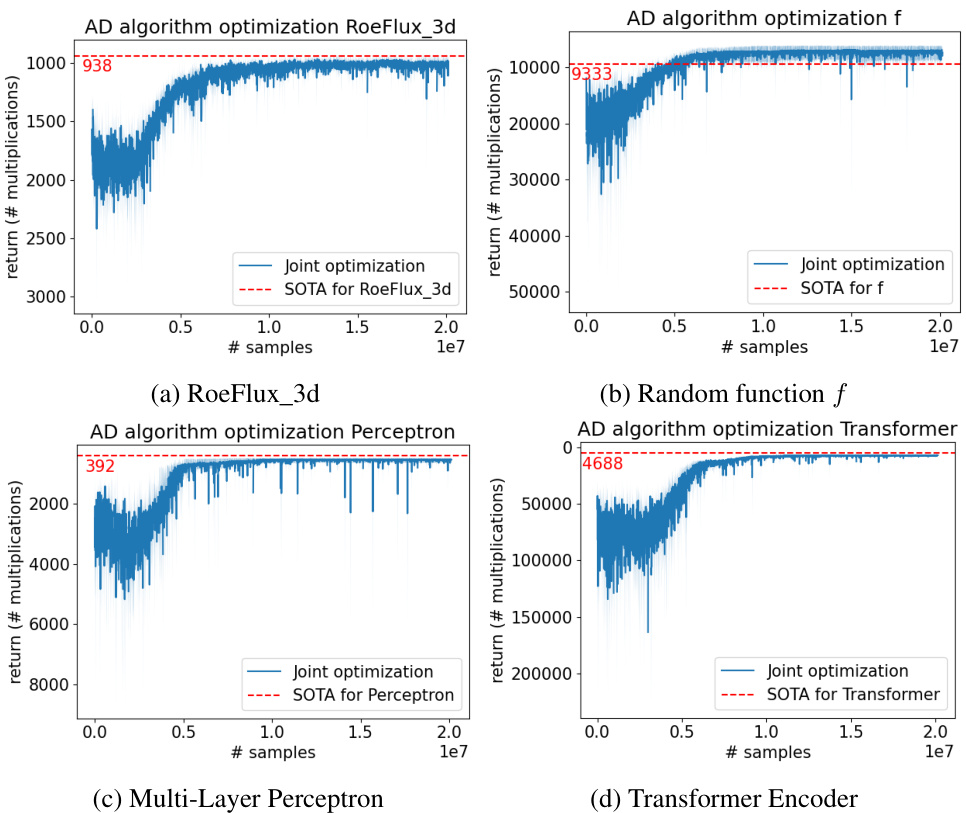
This table presents the best number of multiplications achieved by the AlphaZero-based reinforcement learning agent when trained on all tasks simultaneously (joint training). The results show the number of multiplications required for computing the Jacobian for several tasks from different domains. It allows a comparison to the best results achieved by training the agent on a single task at a time (as seen in Table 1). ’n.a.’ indicates that no improved elimination order was found for that task using the joint training method.

This table presents the number of multiplications needed for Jacobian computation using different methods. It compares the performance of AlphaGrad (a novel method using deep reinforcement learning) against three baselines: forward-mode AD, reverse-mode AD, and minimal Markowitz degree. The results are shown for various tasks from different domains, highlighting AlphaGrad’s improvements. The table also notes the use of a log-scaling of the cumulative reward for some tasks and provides results for both 50 and 250 Monte Carlo Tree Search simulations.
Full paper#