Thompson Sampling For Combinatorial Bandits: Polynomial Regret and Mismatched Sampling Paradox

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in combinatorial bandits because it addresses the long-standing issue of Thompson Sampling’s exponential regret, offering a novel variant with polynomial regret. This breakthrough impacts algorithm design and theoretical understanding, opening new avenues for improved efficiency and broader applicability in various domains.

Visual Insights

#

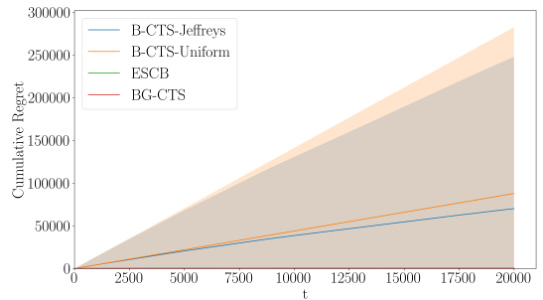
The figure shows two plots: (a) displays the average cumulative regret over time for four algorithms (B-CTS-Jeffreys, B-CTS-Uniform, ESCB, and BG-CTS) in a combinatorial bandit problem with a time horizon of T = 2 × 104 and m = 50. The plot includes error bars representing two standard deviations. (b) displays the average final regret as a function of the number of items (m) for the same four algorithms, with a time horizon of T = 1 × 104 and m varying from 5 to 65. The plot illustrates the polynomial relationship between regret and m for BG-CTS and ESCB, while B-CTS-Jeffreys and B-CTS-Uniform show exponential growth.

In-depth insights

#

Comb Bandits

#

Combinatorial bandits, often shortened to “Comb Bandits,” represent a significant extension of the classic multi-armed bandit problem. Instead of selecting a single arm, a learner must choose a subset of arms (a combination), often subject to constraints such as cardinality or matroid restrictions. This leads to a substantially richer problem landscape. The reward structure, frequently linear, depends on the chosen combination and potentially unknown environmental factors. The challenge lies in balancing exploration (trying different combinations) and exploitation (choosing the seemingly best combination based on past observations). Efficient algorithms for combinatorial bandits are crucial in many applications where simultaneous resource allocation is key. They are essential for applications ranging from online advertising and recommendation systems to resource allocation in networks and sensor management. The algorithms designed often involve sophisticated techniques from linear algebra and optimization to handle the combinatorial complexity. A key aspect is managing the exploration-exploitation trade-off effectively, often through sophisticated upper confidence bound (UCB) methods or Thompson sampling approaches.

Thompson Sampling

#

Thompson Sampling (TS) is a powerful algorithm for solving the exploration-exploitation dilemma in reinforcement learning and bandit problems. The core idea is to sample from the posterior distribution of the reward parameters to decide which action to take next. This approach elegantly balances exploration (trying out less-certain actions) and exploitation (favoring actions with high expected rewards). The paper highlights the strengths and limitations of TS in the context of combinatorial bandits, a more complex setting compared to simple multi-armed bandits. The authors’ analysis reveals that the algorithm’s performance can be surprisingly sensitive to the choice of the posterior sampling distribution and also points out a mismatched sampling paradox. While TS generally boasts low computational complexity, naive application in high-dimensional problems can lead to exponentially growing regret. The proposed algorithm addresses these limitations by introducing carefully designed exploration boosts. Ultimately, the paper contributes to a deeper understanding of TS’s theoretical properties and its effectiveness in practical scenarios.

Regret Analysis

#

The section titled ‘Regret Analysis’ would delve into a rigorous mathematical examination of the algorithm’s performance, specifically focusing on the regret, a crucial metric measuring the difference between the rewards obtained by an optimal strategy and those achieved by the proposed algorithm. The analysis would likely involve probability theory, concentration inequalities, and potentially, martingale techniques. The core goal is to establish upper bounds on the regret, demonstrating that the algorithm’s cumulative loss over time remains within acceptable limits, ideally proving polynomial regret growth with respect to time, the number of arms, and problem dimension. This is crucial because exponential regret is generally unacceptable for practical applications. A key aspect of the analysis would involve careful treatment of the exploration-exploitation trade-off, showing how the algorithm’s strategy effectively balances exploring less-known options with exploiting current knowledge to optimize reward. The proofs presented in this section would be pivotal, demonstrating the correctness of derived bounds and offering a deep understanding of the algorithm’s theoretical guarantees. A successful regret analysis would rigorously establish the algorithm’s efficiency and suitability for large-scale problems.

Mismatched Paradox

#

The “Mismatched Sampling Paradox” highlights a surprising phenomenon in Thompson Sampling (TS) for combinatorial bandits. Contrary to intuition, a TS algorithm using an incorrect likelihood function (mismatched TS) can significantly outperform a TS algorithm using the correct likelihood function (natural TS). This paradox arises because the mismatched TS, by sampling from a simpler, potentially less accurate posterior, may explore the action space more effectively, leading to faster convergence and lower regret. The use of an improper prior in the mismatched TS further contributes to this unexpected behavior. This result challenges the conventional wisdom that a perfectly informed model always leads to better performance and suggests that a degree of model misspecification can be beneficial for exploration. The paradox underscores the intricate interplay between exploration and exploitation in reinforcement learning and raises questions about the optimal balance between model accuracy and exploration strategy in TS for combinatorial bandits.

Future of TS

#

Thompson Sampling (TS) has emerged as a powerful algorithm for solving stochastic bandit problems, demonstrating strong empirical performance. Future research should focus on extending TS’s applicability to more complex settings, such as those with non-stationary rewards, non-linear relationships, or high-dimensional action spaces. Addressing the computational challenges associated with TS in high-dimensional problems is crucial. This could involve developing more efficient sampling techniques or approximation methods. A deeper theoretical understanding of TS’s behavior in various contexts is also needed. This would include rigorous analysis of its regret bounds and convergence properties under different assumptions, particularly concerning its robustness to model misspecification. Finally, further investigation into the interplay between TS and other algorithms is warranted. Exploring hybrid approaches that combine the benefits of TS with other methods could lead to improved performance and broader applicability.

More visual insights

#

More on figures

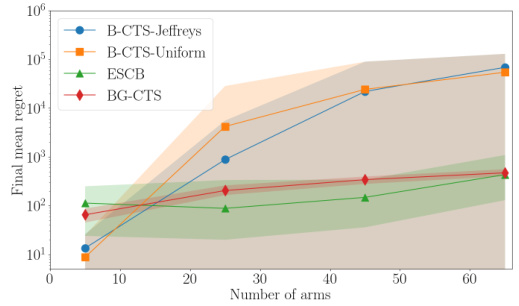
The figure shows the average final regret of four algorithms (B-CTS-Jeffreys, B-CTS-Uniform, ESCB, and BG-CTS) as a function of the number of arms (m). The x-axis represents the number of arms (m), ranging from approximately 5 to 65. The y-axis represents the average final regret on a logarithmic scale. The plot reveals that the regret of B-CTS-Jeffreys and B-CTS-Uniform increases exponentially with m, while ESCB and BG-CTS exhibit much lower regret, demonstrating the effectiveness of these algorithms when the number of arms increases.

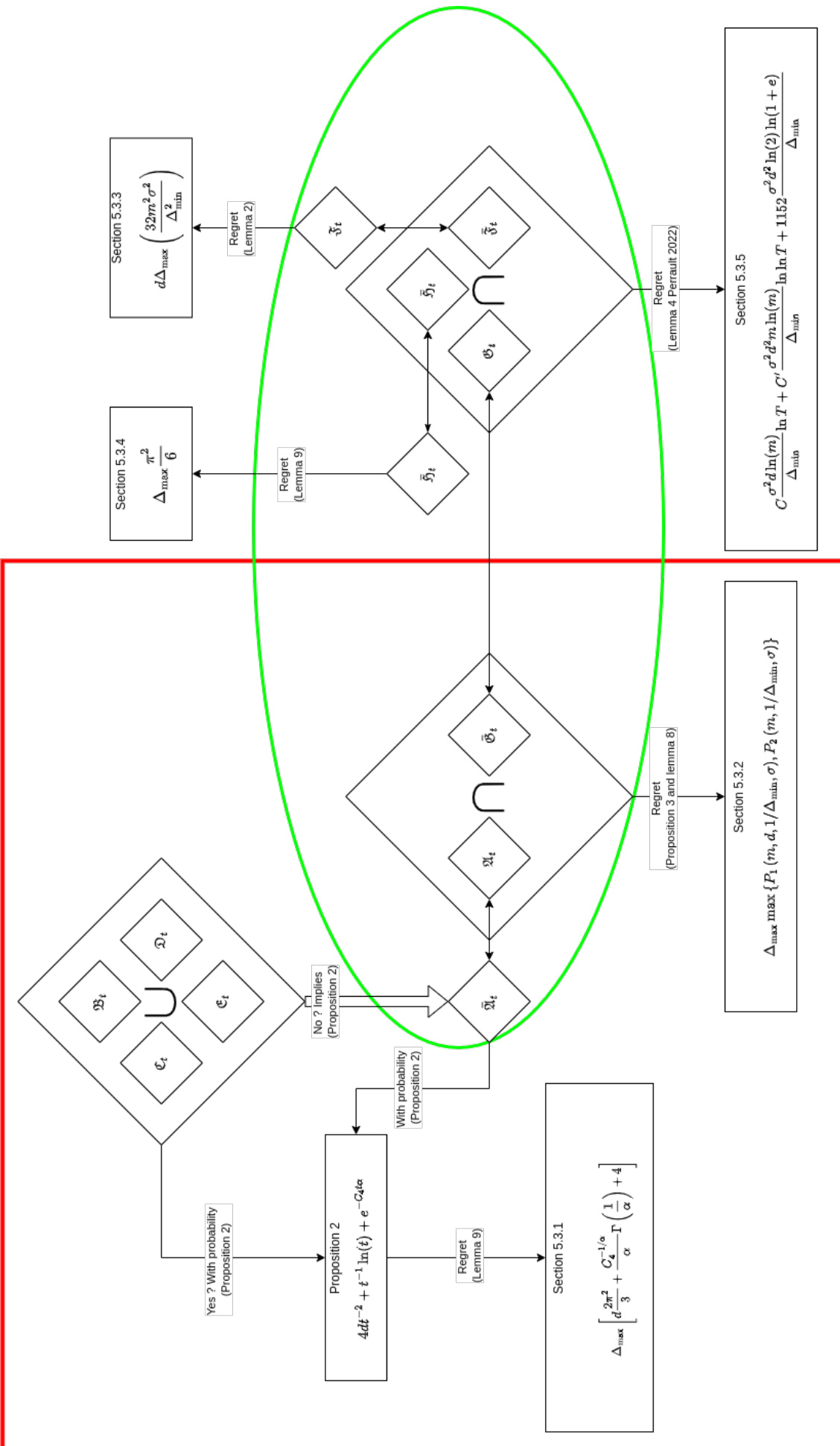
This figure is a flowchart that illustrates the main steps of the proof for the regret upper bound of the BG-CTS algorithm. It breaks down the proof into different events and lemmas, showing how the probability of each event and the corresponding regret are bounded. The flowchart starts by considering a clean run, which happens with high probability, and then analyses the regret based on whether the algorithm sampled the optimal action enough times, and how much the Thompson samples deviate from the expected rewards. The diagram visually depicts the logical flow of the proof and how different parts contribute to the overall regret bound.

Full paper

#