↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Reinforcement learning (RL) algorithms struggle with high sample complexity, the number of interactions needed to learn an optimal policy. Existing algorithms, even those with instance-dependent (problem-specific) guarantees, often rely on separately estimating each policy’s value, which can be inefficient. This paper investigates a more efficient approach: focusing on the differences between policies rather than their individual values. This is known to be successful in simpler bandit problems.
The research shows that directly estimating policy differences in tabular RL isn’t sufficient to guarantee optimal sample complexity. However, a new algorithm called PERP is introduced. PERP learns the behavior of a single reference policy and then estimates how other policies deviate from it. This approach significantly improves upon existing bounds, providing the tightest known sample complexity for tabular RL. The findings highlight a fundamental difference between contextual bandit settings and full RL, offering new insights into the challenges of efficient RL algorithm design.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning because it significantly advances our understanding of sample complexity, a critical factor limiting the applicability of RL algorithms. The paper’s focus on instance-dependent complexity is particularly relevant given the current trend of moving beyond worst-case analysis in favor of more nuanced evaluation metrics. The novel algorithm and refined bounds provide a significant step towards more efficient and effective RL methods, thus opening new avenues for developing practically applicable algorithms.
Visual Insights#
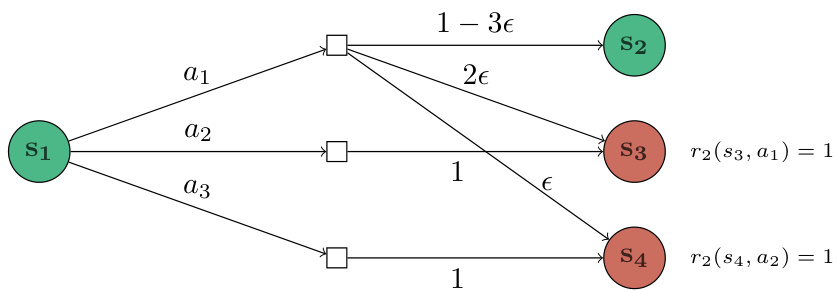
This figure shows a simple Markov Decision Process (MDP) with four states and three actions. Two policies, π1 and π2 are defined; π1 always takes action a1, while π2 takes action a2 in the red states (s3 and s4) and a1 otherwise. The key point illustrated is that the difference in state-action visitations between π1 and π2 is only significant in the red states and negligible elsewhere. This motivates the idea that estimating only the difference between policy values can be more efficient than estimating the value of each policy individually.

This table lists the notations used throughout the paper, providing a comprehensive description of each symbol and its meaning. It includes notations for state and action spaces, policies, rewards, value functions, complexities, and algorithm-specific variables.
Full paper#



















