↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many machine learning and reinforcement learning algorithms rely on stochastic approximation (SA) to iteratively solve fixed-point equations using noisy data. Existing analyses of SA often simplify by assuming either independent and identically distributed (i.i.d.) data or linear update rules. However, real-world data often exhibits dependencies (Markovian data) and algorithms frequently employ nonlinear update rules, making these assumptions unrealistic. The interaction between Markovian dependence and nonlinearity presents significant analytical challenges not captured by prior techniques, leading to obstacles in establishing weak convergence and characterizing the asymptotic bias of SA algorithms.
This paper tackles these challenges head-on. By carefully examining the simultaneous presence of Markovian data and nonlinear update rules, the authors develop a fine-grained analysis leveraging smoothness and recurrence properties of SA updates. This allows them to derive, for the first time, the weak convergence of the joint process of Markovian data and SA iterates. The asymptotic bias is precisely characterized, revealing a previously unknown multiplicative interaction between the Markovian noise and nonlinearity. Moreover, the paper provides finite-time bounds on higher moments and establishes a central limit theorem, offering valuable tools for both asymptotic and non-asymptotic analyses.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with stochastic approximation algorithms, especially in machine learning and reinforcement learning. It addresses the limitations of existing methods by handling nonlinear updates and Markovian data simultaneously, which are common scenarios in modern applications. The paper’s findings will improve the accuracy and efficiency of such algorithms and offers new avenues for research into bias reduction and variance control.
Visual Insights#
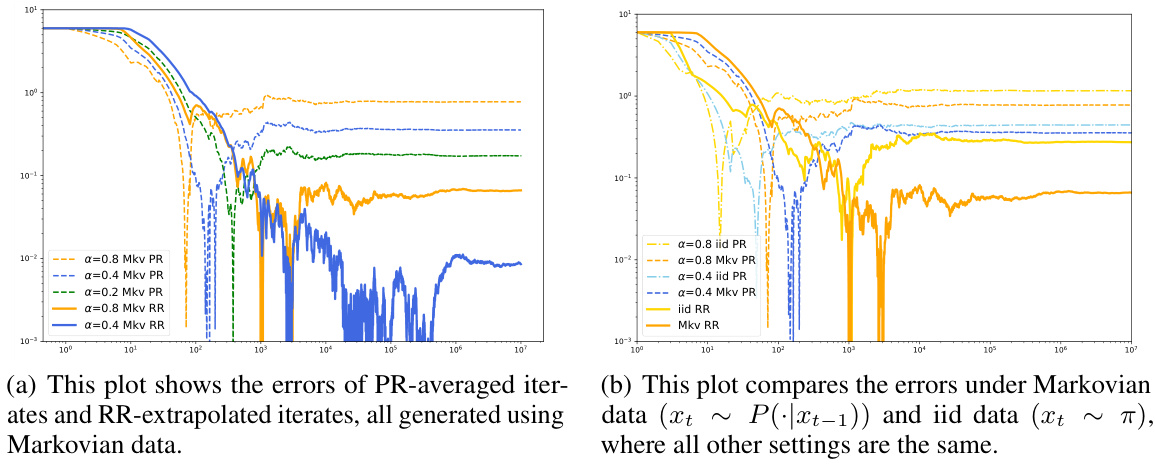
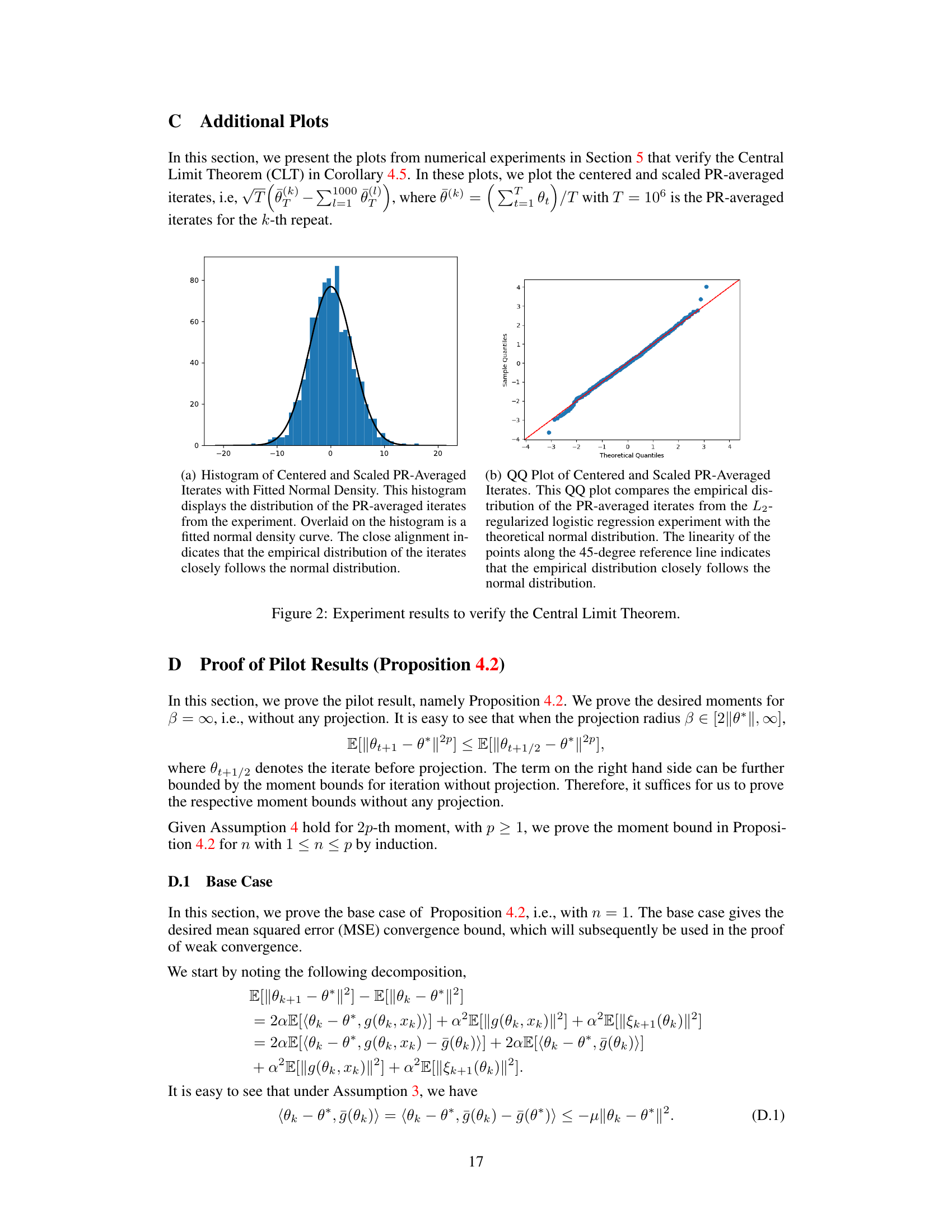
This figure consists of two subfigures. Subfigure (a) shows the errors of PR-averaged iterates and RR-extrapolated iterates, all generated using Markovian data. Different stepsizes (α = 0.8, 0.4, 0.2) are used for both PR and RR methods. The plot shows that RR extrapolation significantly reduces the bias compared to PR averaging. Subfigure (b) compares the errors under Markovian data (xt+1 ~ P(·|xt)) and i.i.d. data (xt ~ π) with the same stepsizes. The plot indicates that Markovian data does not necessarily result in a larger bias than i.i.d. data, highlighting the complex interplay between nonlinearity and Markovian structures.
In-depth insights#
Markovian SA#
The concept of Markovian Stochastic Approximation (SA) introduces a significant departure from traditional SA by incorporating the temporal dependence of data. Instead of assuming independent and identically distributed (i.i.d.) data points, Markovian SA acknowledges that consecutive data points are correlated, forming a Markov chain. This correlation structure is particularly relevant in many real-world applications, such as reinforcement learning and time series analysis, where the current state is heavily influenced by the preceding one. Analyzing Markovian SA presents considerable challenges, as the standard techniques used for i.i.d. SA fail to account for the intricate dependencies between data points. The core difficulty lies in the correlation between the Markov chain’s state and the algorithm’s iterates, leading to more complex bias structures and convergence properties that must be carefully addressed. Consequently, research in Markovian SA often focuses on developing new analysis methods to handle the correlated data, such as coupling arguments and sophisticated Lyapunov function techniques to account for the serial dependence and establish convergence rates and bias characterizations. These theoretical insights have substantial practical ramifications, offering improved understanding and more robust algorithms for applications where data dependencies are crucial.
Nonlinearity Effects#
The phenomenon of nonlinearity significantly impacts stochastic approximation (SA) algorithms, particularly when coupled with Markovian data. Nonlinearity introduces complexities in the analysis because standard linear techniques are no longer applicable. The interaction between nonlinear updates and Markovian data dependence creates challenges in establishing weak convergence, especially regarding the asymptotic bias. A key contribution of the paper is to carefully delineate how these two structures interact to produce a more intricate bias than previously understood, showing a multiplicative effect. This nuanced analysis goes beyond prior works that focused on i.i.d data or linear updates, leading to a more precise characterization of the asymptotic bias, including terms capturing the interplay between the Markovian noise and the nonlinearity of the updates. The presence of these combined terms necessitates more refined analytical techniques to achieve convergence and bias characterization. Understanding these nonlinear effects is critical for developing more robust and accurate SA algorithms. The impact extends to algorithm design choices, particularly regarding bias reduction strategies like Polyak-Ruppert averaging and Richardson-Romberg extrapolation, which are shown to have differing effects depending on the nonlinearity and Markovian structure.
Bias Decomposition#
The heading ‘Bias Decomposition’ suggests a detailed analysis of the various contributing factors to the asymptotic bias observed in stochastic approximation (SA) algorithms. The authors likely delve into separating the bias into distinct components, each stemming from different sources. This could include a bias term due to Markovian data dependence, capturing the effect of temporal correlation in the data sequence. There would also likely be a component attributed to the nonlinearity of the SA update function, highlighting how the nonlinearity itself introduces bias. Critically, a multiplicative interaction term between the Markovian dependency and nonlinearity is probable. This is a key insight, demonstrating how these two factors do not simply add their individual biases, but instead exhibit a more complex, intertwined effect on the overall bias. The decomposition allows for a more nuanced understanding of the bias, paving the way for designing better bias reduction techniques and potentially improving the accuracy of SA methods, particularly in scenarios involving both Markovian data and nonlinearity.
Convergence Rates#
The analysis of convergence rates in stochastic approximation (SA) algorithms is crucial for understanding their efficiency and practicality. Constant step-size SA presents unique challenges compared to diminishing step-size methods. This paper addresses this by providing finite-time bounds on the higher moments of the error, which are essential for understanding the algorithm’s behavior beyond the mean. The geometric convergence rates established help quantify the speed of convergence, providing insights into the algorithm’s efficiency relative to others. The analysis also accounts for the interplay of Markovian data dependence and nonlinear update functions, factors typically not considered simultaneously in previous studies. The results provide non-asymptotic guarantees for constant step-size SA, which are more valuable in practice than asymptotic results. Finally, the Central Limit Theorem provides crucial support for statistical inference, empowering reliable analysis and decision-making based on the algorithm’s output.
Future Work#
The paper’s lack of a dedicated “Future Work” section is a missed opportunity. Extending the analysis to non-countable state spaces would significantly broaden the applicability of the presented theoretical results. Investigating the dimension dependence of the bias and convergence rates is crucial for practical implementations. Exploring the impact of different noise structures beyond the assumed i.i.d. and Markovian noise could reveal further valuable insights. Relaxing the strong monotonicity assumption would be a significant theoretical advancement and enhance practical usefulness, as many real-world applications do not strictly adhere to this condition. Finally, developing efficient bias reduction techniques for nonlinear Markov SA, beyond the explored methods, warrants further investigation. This could involve exploring alternative averaging schemes or extrapolation methods.
More visual insights#
More on figures
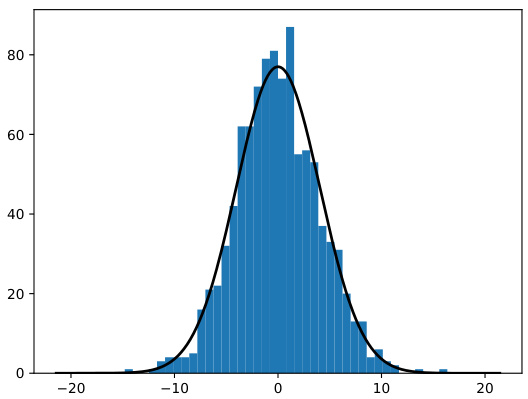
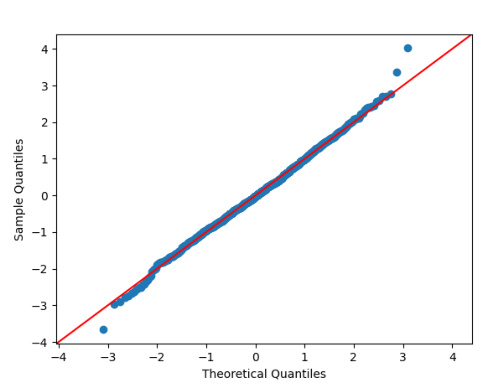
This figure contains two subfigures, (a) and (b). Subfigure (a) is a histogram of the centered and scaled PR-averaged iterates from the experiment, overlaid with a fitted normal density curve. The close alignment indicates that the empirical distribution closely follows the normal distribution. Subfigure (b) is a QQ plot that compares the empirical distribution of the PR-averaged iterates from the L2-regularized logistic regression experiment with the theoretical normal distribution. The linearity of the points along the 45-degree reference line indicates that the empirical distribution closely follows the normal distribution. These plots verify the Central Limit Theorem (CLT) for the averaged iterates from the experiment.
This figure contains two subfigures. Subfigure (a) shows the errors of PR-averaged iterates and RR-extrapolated iterates, generated using Markovian data. The results show that RR extrapolation effectively reduces the bias compared to PR averaging. Subfigure (b) compares the errors under Markovian data and i.i.d. data, showing that Markovian data does not necessarily result in a larger bias than i.i.d. data, consistent with the theoretical findings.
Full paper#