Logarithmic Smoothing for Pessimistic Off-Policy Evaluation, Selection and Learning

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on offline contextual bandits because it introduces a novel, more robust method for policy evaluation, selection, and learning. It addresses the critical issue of high variance in existing methods by proposing logarithmic smoothing, offering tighter concentration bounds and improved performance. This work is relevant to current trends in pessimistic offline RL and opens new avenues for more reliable decision-making under uncertainty.

Visual Insights

#

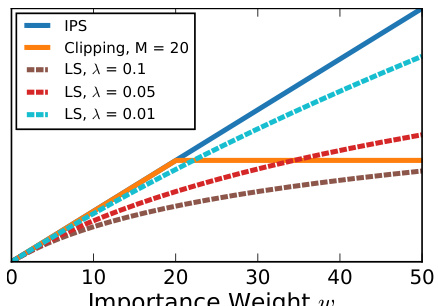
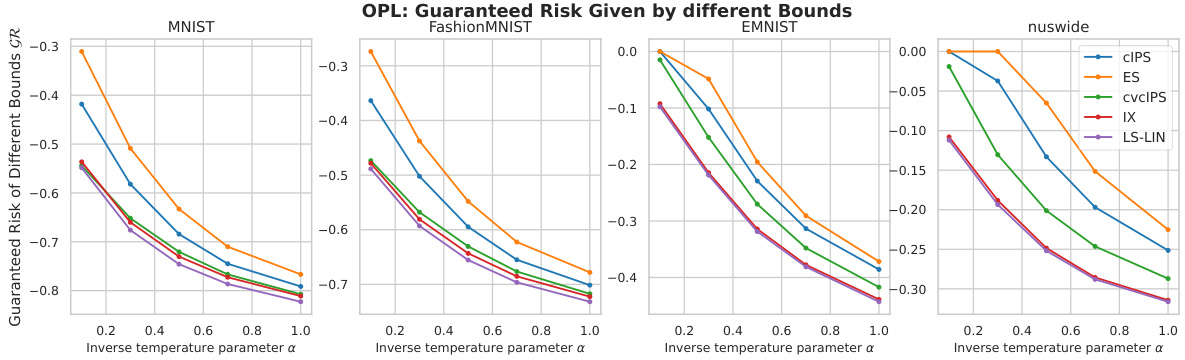
This figure shows the Logarithmic Smoothing (LS) estimator with different λ values. The x-axis represents the importance weight ωπ, and the y-axis represents the value of the LS estimator for various values of λ. The figure also includes lines for the standard IPS estimator and the Clipping estimator for comparison, illustrating the bias-variance trade-off of the LS estimator as λ changes. As λ increases, the variance of the LS estimator decreases but its bias increases.

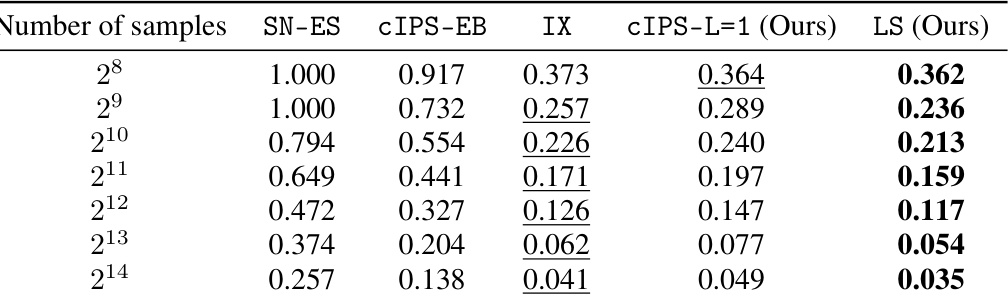
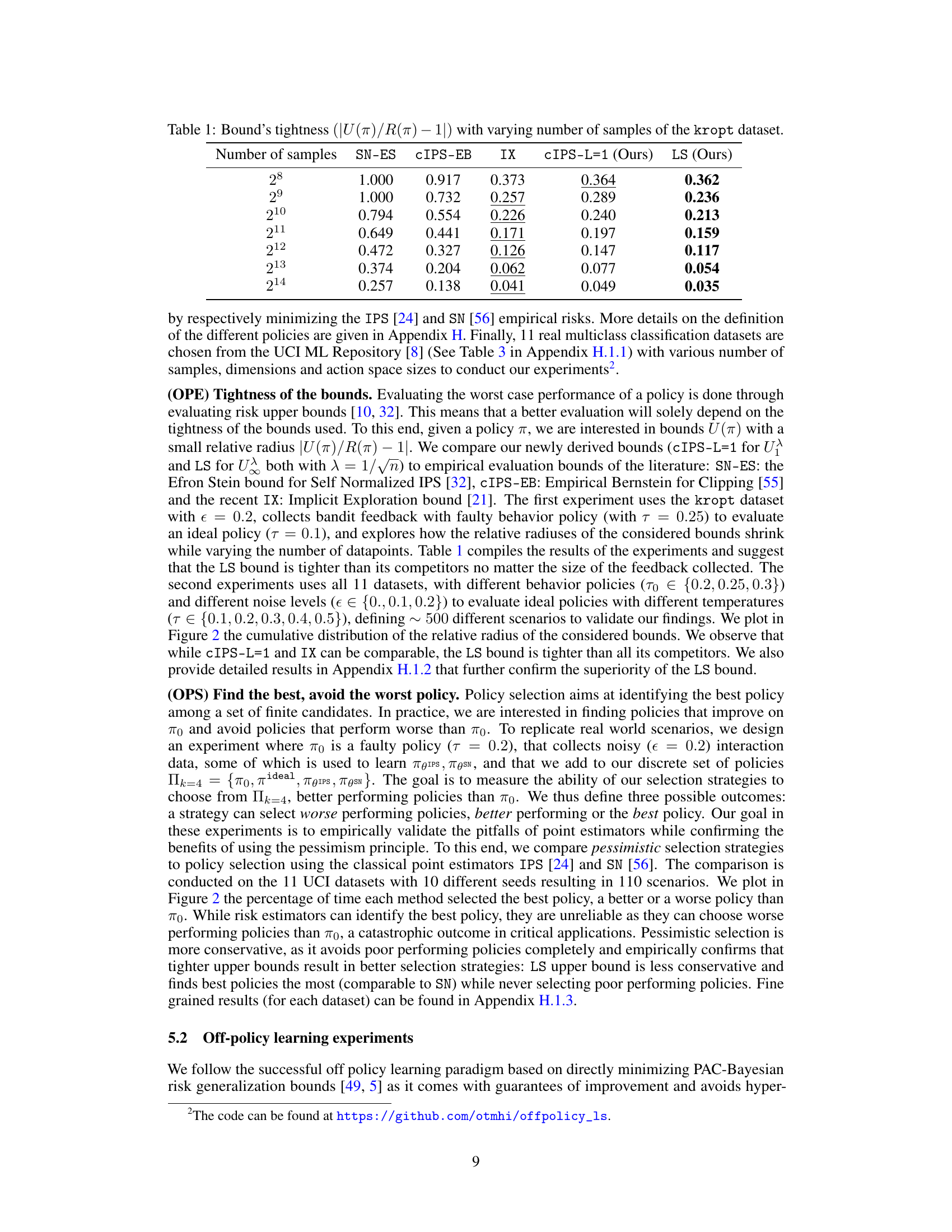
This table presents the tightness of different risk upper bounds for a given policy (π) with varying sample sizes from the kropt dataset. The tightness is measured by the relative radius |U(π)/R(π) – 1|, where U(π) represents the risk upper bound and R(π) the true risk. Lower values indicate tighter bounds, implying better worst-case risk assessment. The table compares the proposed Logarithmic Smoothing (LS) method with existing methods, such as SN-ES, CIPS-EB, IX, and cIPS-L=1. The results demonstrate the improved tightness of LS bound across different sample sizes.

In-depth insights

#

Pessimistic OPE

#

Pessimistic Offline Policy Evaluation (OPE) offers a robust approach to evaluating the performance of policies learned from historical data by constructing high-probability upper bounds on the true risk. Unlike traditional OPE methods that focus on point estimates which can be unreliable, pessimistic OPE provides confidence intervals, making it particularly suitable for high-stakes decision-making scenarios. The core idea is to quantify the worst-case performance, enabling a more conservative yet reliable evaluation that accounts for uncertainty inherent in offline data. This approach is critical because standard OPE estimators often suffer from high variance and thus produce unreliable risk estimates, especially when the behavior and target policies significantly differ. The tightness of the upper bounds is key; tighter bounds translate to more accurate risk assessments and better-informed policy selection. The development of novel, fully empirical concentration bounds for a broad class of importance weighting risk estimators is a significant contribution. Methods like logarithmic smoothing are introduced to achieve tighter bounds, improving upon the performance of existing techniques. Pessimistic OPE’s inherent robustness makes it a valuable tool where confidence in the evaluation is paramount.

LS Estimator

#

The Logarithmic Smoothing (LS) estimator, a core contribution of the paper, addresses the high variance issue inherent in Inverse Propensity Score (IPS) estimators commonly used for off-policy evaluation in contextual bandits. LS achieves this by logarithmically smoothing large importance weights, thereby mitigating the instability caused by extreme weights. This smoothing technique is shown to yield a tighter concentration bound than competing methods, leading to improved performance in policy selection and learning. The theoretical analysis rigorously establishes the benefits of LS, including its sub-Gaussian concentration properties, and demonstrating the estimator’s ability to provide a tighter high-probability upper bound on the risk than existing methods. Empirical results further validate the efficacy of LS, showcasing improved performance in various settings across multiple datasets. The versatility of LS is highlighted by its applicability in diverse tasks: pessimistic off-policy evaluation, selection, and learning, making it a valuable tool for real-world decision-making under uncertainty. The design of LS stems from a principled approach of searching for the estimator within a broad class of regularized IPS estimators which minimizes the concentration bound, rather than choosing an estimator a priori for ease of analysis, highlighting a novel and effective strategy for constructing robust risk estimators. The favorable performance of LS, both in terms of theoretical guarantees and empirical results, positions it as a significant advance in the field of offline contextual bandit learning.

OPS & OPL

#

The sections on “Off-Policy Selection (OPS)” and “Off-Policy Learning (OPL)” present a significant contribution to the field of offline contextual bandits. OPS focuses on efficiently selecting the best policy from a finite set, a critical task in many real-world applications. The paper leverages the developed pessimistic OPE framework to devise a novel OPS strategy, directly minimizing the risk estimator without requiring complex calculations. This strategy boasts favorable theoretical properties, including low suboptimality, and excels in empirical evaluations, outperforming existing methods. OPL tackles the more challenging problem of learning an optimal policy from an infinite set. The paper extends the pessimistic framework into a PAC-Bayesian setting, providing strong theoretical guarantees. A novel, linearized estimator is introduced to facilitate the analysis. The resulting learning algorithm effectively balances exploration and exploitation, minimizing a theoretically-justified upper bound on the risk. The empirical results firmly support the effectiveness of both the proposed OPS and OPL strategies, demonstrating their versatility and superior performance.

PAC-Bayesian Bounds

#

PAC-Bayesian bounds offer a powerful framework for analyzing the generalization performance of machine learning models, particularly in scenarios with limited data or complex model structures. They provide finite-sample guarantees, unlike traditional asymptotic bounds, making them suitable for practical applications. The core idea involves bounding the risk of a posterior distribution over model parameters, given a prior distribution and observed data. This is achieved by leveraging the Kullback-Leibler (KL) divergence, a measure of distance between the prior and posterior. Tighter bounds are obtained by carefully selecting the prior and incorporating data-dependent aspects into the analysis. The strength of PAC-Bayesian bounds lies in their flexibility; they can be adapted to various model types and learning algorithms, offering a versatile tool for theoretical analysis and algorithm design. However, the tightness of the bounds often relies on the choice of the prior and the complexity of the model, which can impact their practical applicability. Recent research focuses on developing techniques for optimizing bounds and making them more readily usable in real-world applications. Overall, PAC-Bayesian bounds represent a significant advancement in statistical learning theory, providing rigorous theoretical justification for the performance of machine learning models.

Future Work

#

The research paper’s ‘Future Work’ section could explore several promising avenues. Extending the Logarithmic Smoothing (LS) estimator to handle continuous action spaces is crucial for broader applicability. Current methods often rely on discretization, which can be suboptimal. Investigating the theoretical properties and empirical performance of LS in this setting would be significant. Another key area is relaxing the i.i.d. assumption of the contextual bandit problem. Real-world data frequently exhibits dependencies and non-stationarity. Developing methods that incorporate these complexities will be highly valuable and is essential for moving beyond the limitations of the current work. Finally, integrating LS into more sophisticated offline reinforcement learning (RL) frameworks presents a powerful opportunity. Many offline RL algorithms currently rely on estimators with less favorable concentration properties. This could significantly boost the confidence and performance of offline RL policies, particularly in high-stakes domains where pessimism is essential for safety. Addressing these points would enhance the impact and robustness of the LS method.

More visual insights

#

More on figures

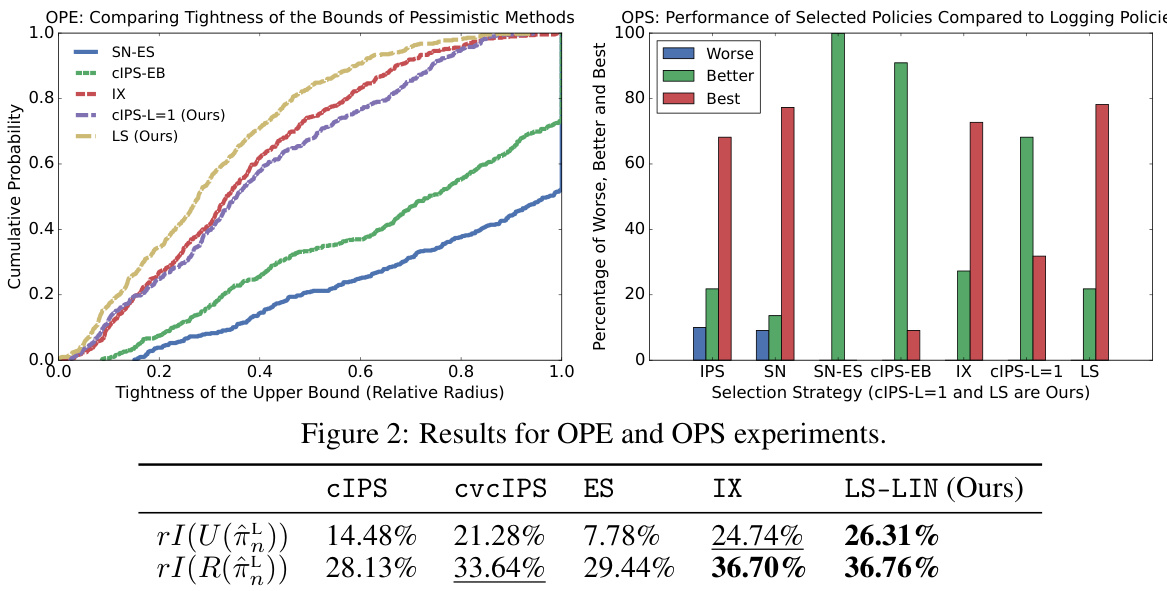
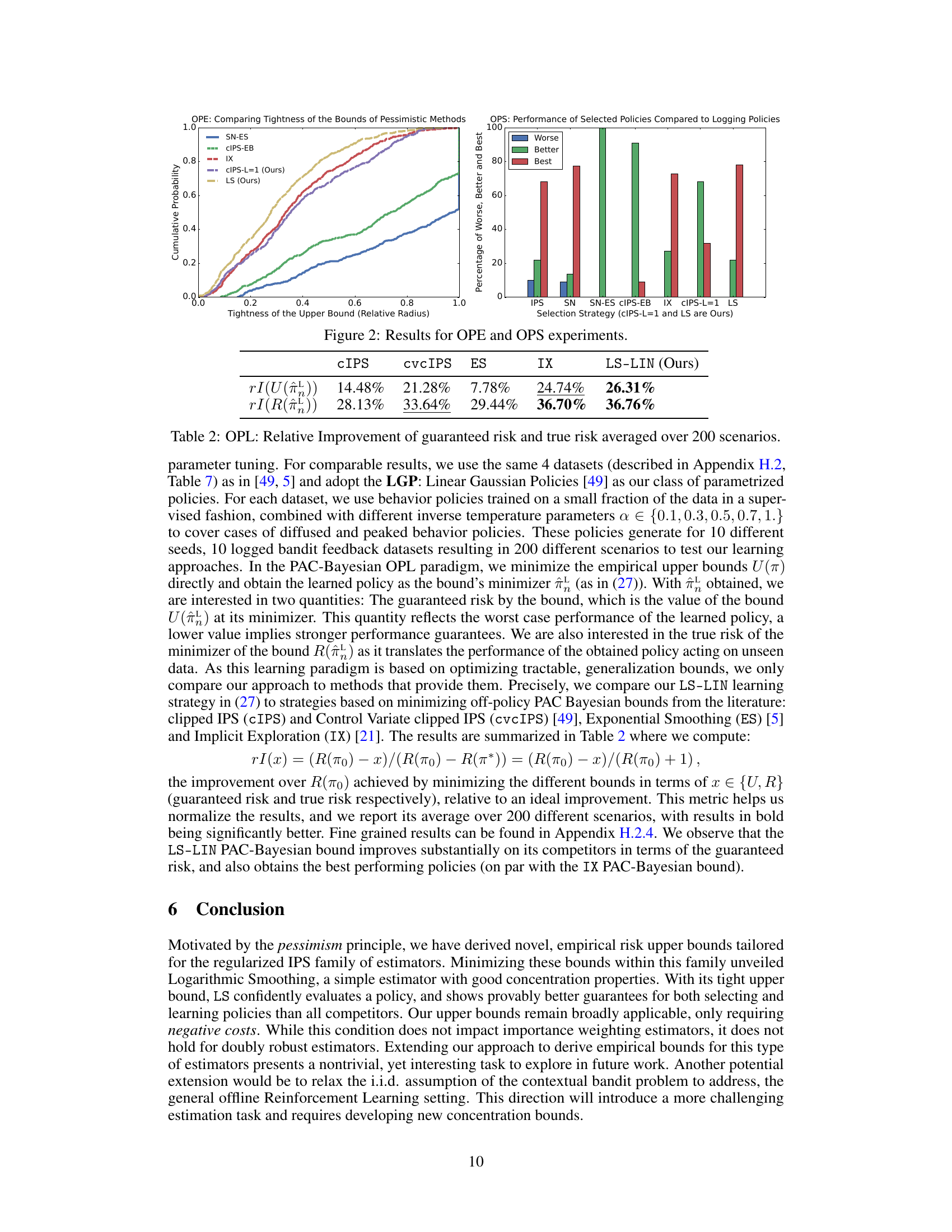
This figure shows the results of experiments comparing different methods for off-policy evaluation (OPE) and off-policy selection (OPS). The left panel shows the cumulative distribution of the relative radius of different upper bounds on the risk, demonstrating that the Logarithmic Smoothing (LS) bound is generally tighter than competing bounds. The right panel shows the performance of various selection strategies on the task of choosing better performing policies than a logging policy, illustrating the advantages of using pessimistic strategies based on tighter upper bounds.

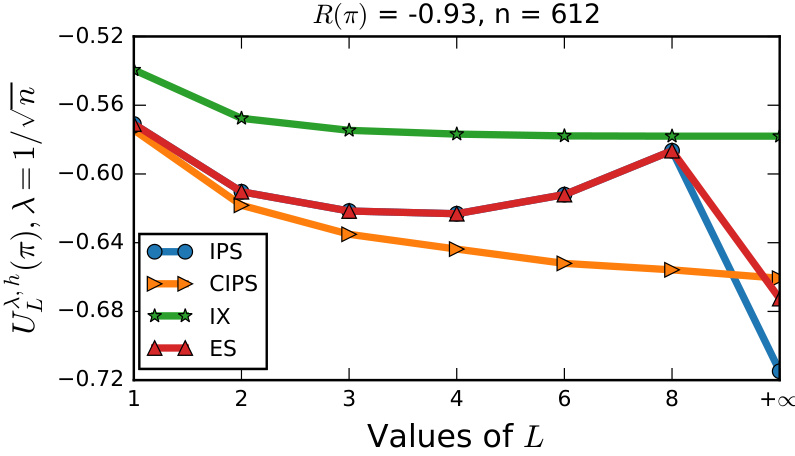
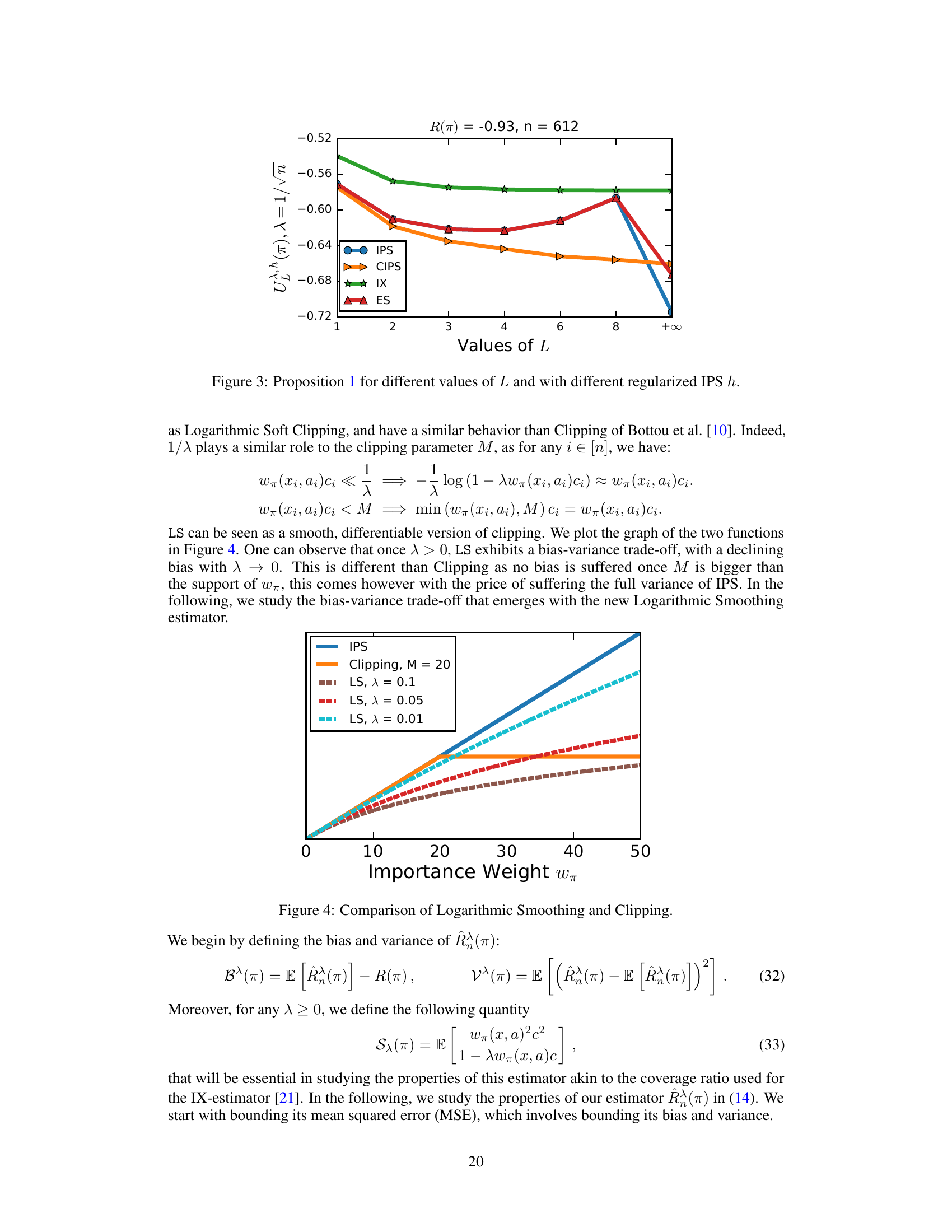
This figure shows the results of evaluating the empirical moments bound (Proposition 1) for different values of L (moment order) and different regularized IPS functions (IPS, Clipped IPS, Implicit Exploration, Exponential Smoothing). It demonstrates how the tightness of the upper bound varies with the number of moments used and different regularizers. The experiment was performed on the ‘balance-scale’ dataset, with parameters λ = √1/n and a fixed policy with R(π) = -0.93.

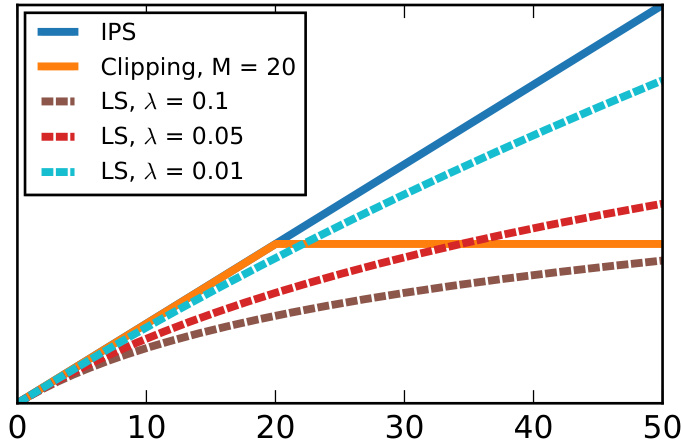
The figure shows the impact of the logarithmic smoothing parameter λ on the Logarithmic Smoothing estimator. When λ = 0, the estimator is equivalent to the standard IPS estimator. As λ increases, the importance weights are smoothed, leading to a bias-variance tradeoff. The plot shows how the LS estimator behaves for different values of λ, demonstrating its ability to control bias and variance.

This figure shows the results of experiments conducted for off-policy evaluation (OPE) and off-policy selection (OPS). The left panel compares the tightness of different risk upper bounds in OPE by plotting the cumulative distribution of their relative radiuses. The right panel shows the performance of different policy selection strategies (IPS, SN, SN-ES, CIPS-EB, IX, CIPS-L=1, and LS) by displaying the percentage of times each strategy selected the best, better, or worse policies than the behavior policy.

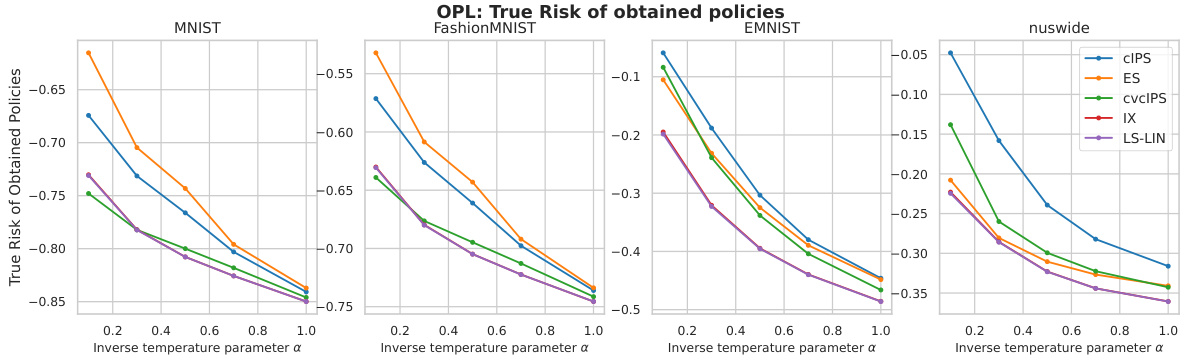
This figure presents the results of experiments conducted for off-policy evaluation (OPE) and off-policy selection (OPS). The left subplot shows a comparison of the tightness of different upper bounds used for OPE, illustrating how the Logarithmic Smoothing (LS) bound provides tighter estimates than existing methods. The right subplot illustrates the performance of various policy selection strategies, highlighting the effectiveness of pessimistic selection approaches using tighter bounds in selecting better-performing policies and avoiding worse ones.

More on tables

This table presents the results of an experiment designed to evaluate the tightness of different risk upper bounds. The experiment uses the kropt dataset and varies the number of samples used to estimate the risk. The table compares the relative radius (|U(π)/R(π) - 1|) of the LS bound to several other bounds from the literature, including SN-ES, CIPS-EB, IX and CIPS-L=1. The results show that LS bound is tighter than the other bounds, indicating better performance in assessing a policy’s worst-case risk.

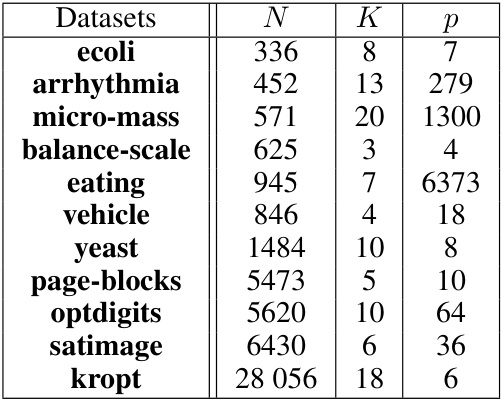
This table presents the tightness of different risk upper bounds for a given policy π, using the relative radius |U(π)/R(π) - 1| as a measure. The tightness of the bound indicates how close the estimated risk is to the true risk. The table shows how the tightness changes as the number of samples in the kropt dataset varies. The bounds compared include SN-ES, CIPS-EB, IX, CIPS-L=1 (ours), and LS (ours).

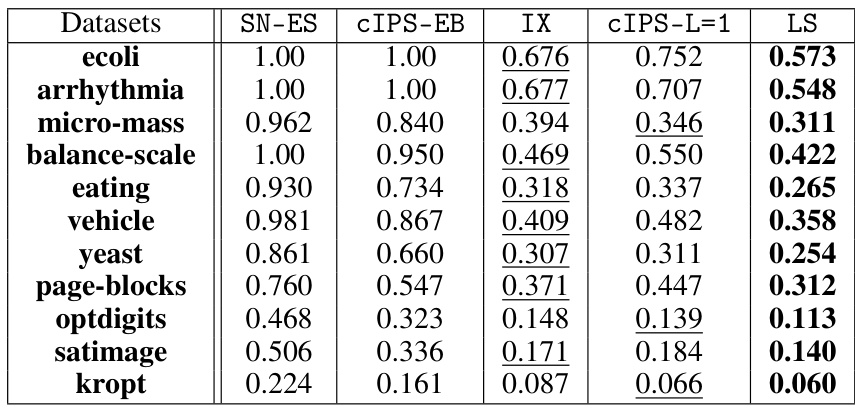
This table presents the average relative radius for different bounds across eleven UCI datasets. The relative radius, |U(π)/R(π) - 1|, measures the tightness of each bound for each dataset, indicating how well the bound approximates the true risk. Lower values indicate tighter bounds and better performance. The bounds compared include SN-ES, CIPS-EB, IX, cIPS-L=1 (the authors’ proposed method), and LS (the authors’ proposed method). The results show that the LS bound consistently outperforms other bounds across all datasets.

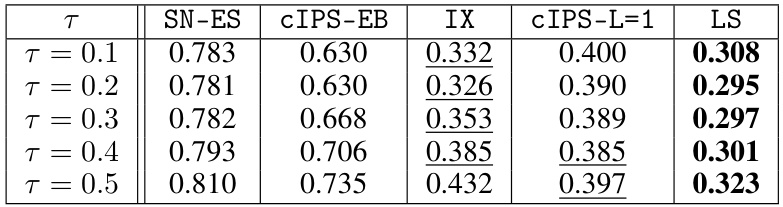
This table presents the average relative radius of different upper bounds for ideal policies with various temperature parameters (τ). The relative radius, |U(π)/R(π) - 1|, measures the tightness of the bound U(π) in estimating the true risk R(π). Lower values indicate tighter bounds, which are preferable for more precise policy evaluation. The table compares the Logarithmic Smoothing (LS) bound with other existing methods, including SN-ES, cIPS-EB, IX, and cIPS-L=1, across different temperature settings to demonstrate its superior performance.

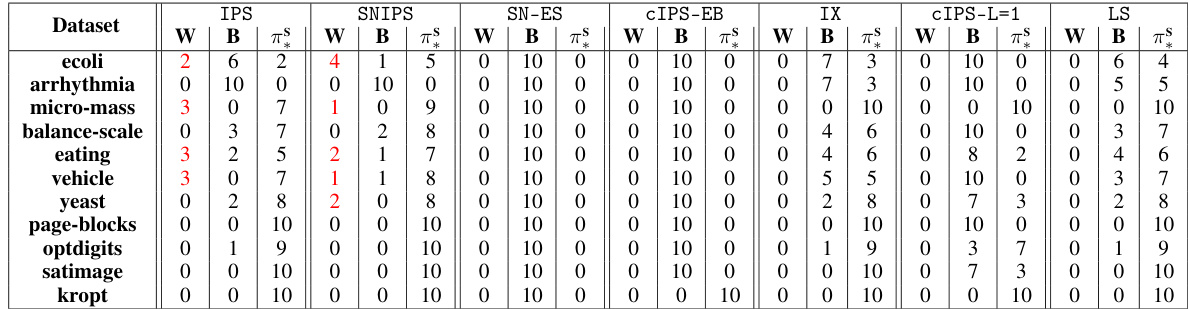
This table presents the results of off-policy selection experiments. For each of the eleven datasets used, it shows how many times each method (IPS, SNIPS, SN-ES, CIPS-EB, IX, cIPS-L=1, LS) selected a policy that performed worse than the behavior policy (W), better than the behavior policy (B), or was the best policy (π). The results highlight the reliability of using upper bounds for policy selection, as they avoid selecting worse-performing policies.

This table presents the results of an experiment evaluating the tightness of different risk upper bounds for offline contextual bandit policy evaluation. The tightness is measured by the relative radius |U(π)/R(π) - 1|, which represents how closely the risk upper bound U(π) approximates the true risk R(π). The experiment uses the kropt dataset and varies the number of samples used to compute the bounds. The table compares five bounds: SN-ES, CIPS-EB, IX, CIPS-L=1 (the authors’ new bound), and LS (the authors’ logarithmic smoothing estimator). The results show the relative radius for each bound with varying numbers of samples. Lower relative radius values indicate tighter bounds and better estimation accuracy.

Full paper

#