NeoRL: Efficient Exploration for Nonepisodic RL

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

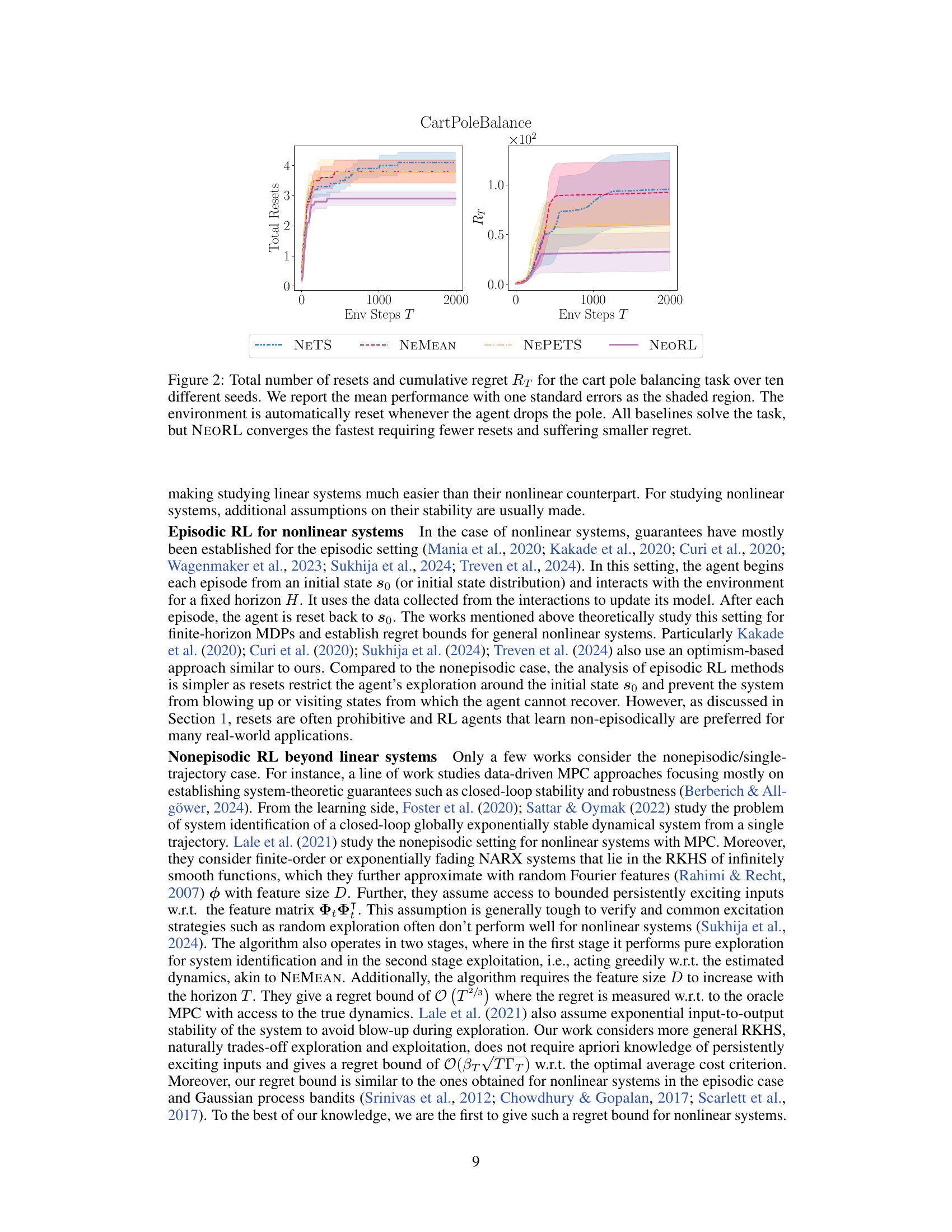
This paper is crucial because it provides the first-of-its-kind regret bound for nonepisodic reinforcement learning in nonlinear systems, a significant advancement in the field. It also introduces NEORL, a novel algorithm demonstrating superior performance in deep RL benchmarks, opening new avenues for online learning in real-world applications where resets are impractical or impossible. This work bridges the gap between theory and practice, making it highly relevant to researchers working on adaptive control and online learning.

Visual Insights

#

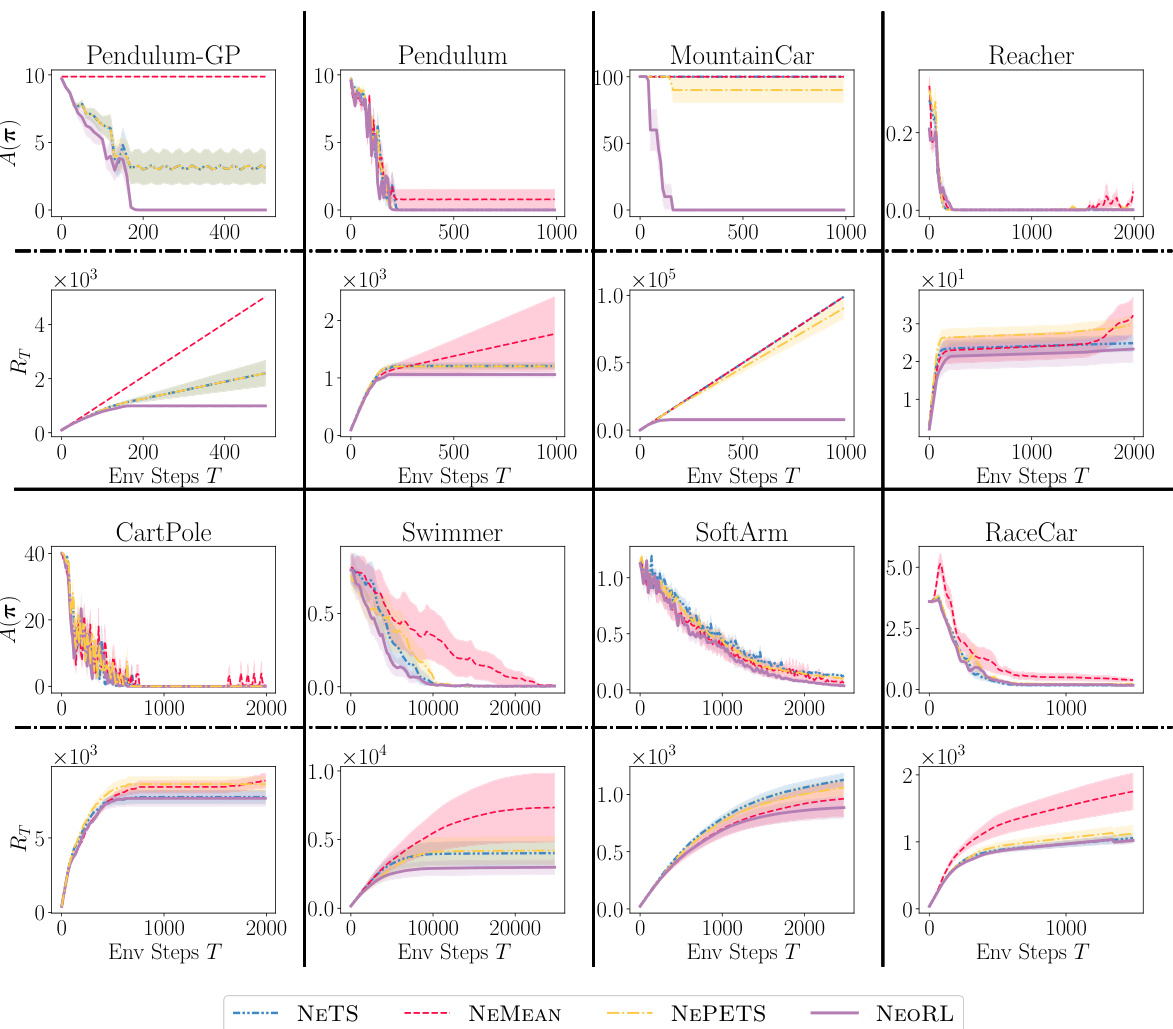
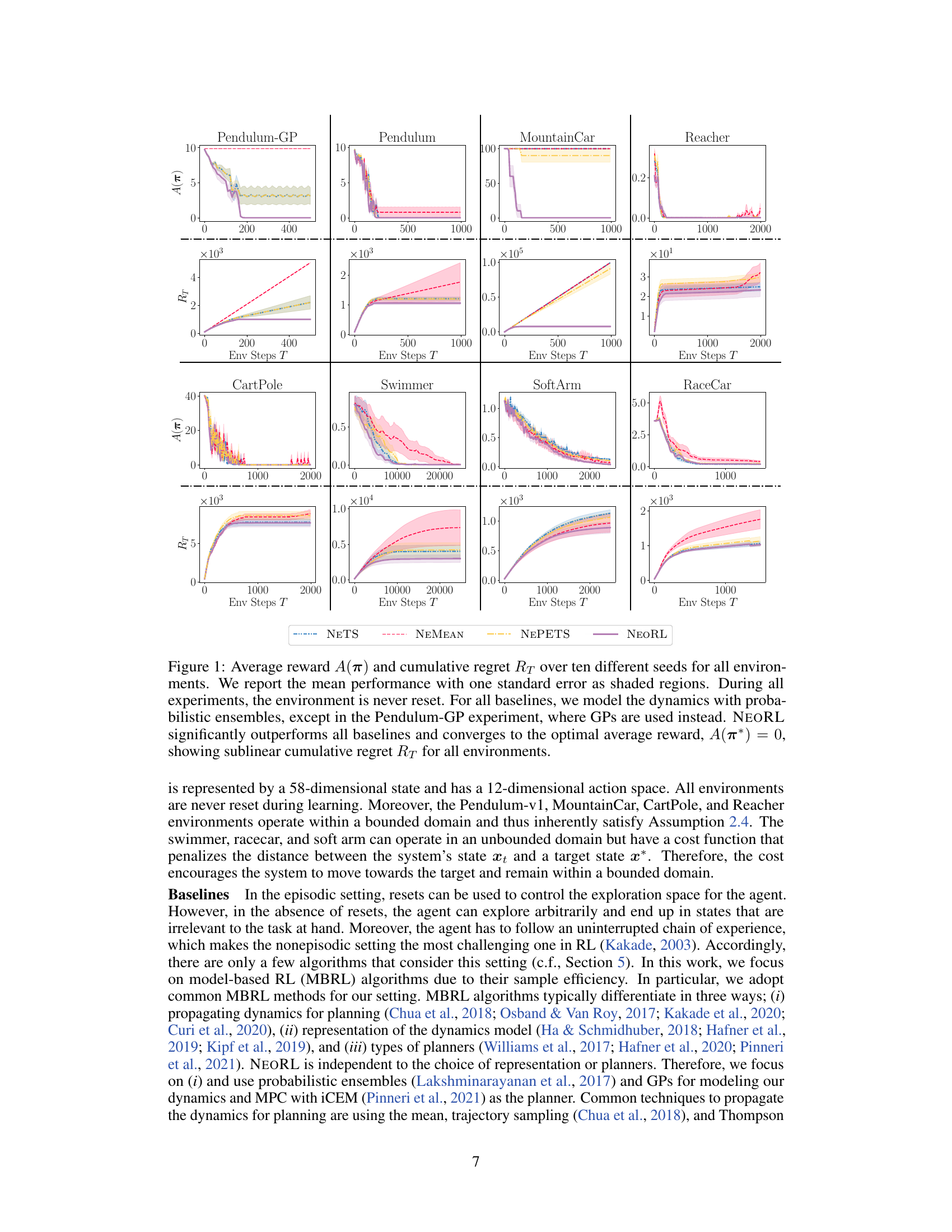
This figure compares the performance of NEORL against other baselines across several reinforcement learning environments. The key takeaway is that NEORL consistently achieves the optimal average reward while exhibiting sublinear cumulative regret, meaning its performance improves more efficiently over time compared to the baselines. The experiments highlight NEORL’s ability to learn effectively in a nonepisodic setting (without resets), a significant advantage in real-world applications where resets are often impractical.

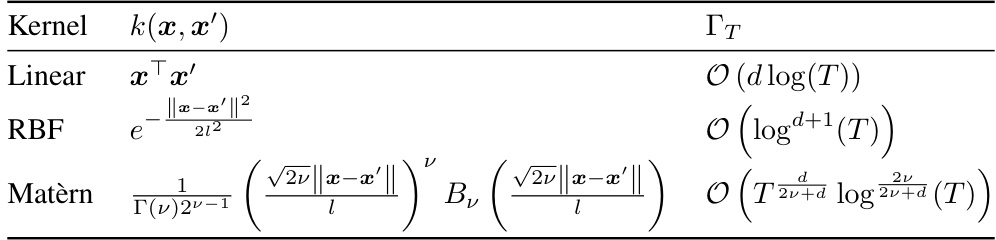
This table shows the upper bounds of the maximum information gain (Γτ ) for three common kernels used in Gaussian processes: Linear, RBF (Radial Basis Function), and Matérn. The maximum information gain is a measure of the complexity of learning a function from data, and these bounds indicate how quickly this complexity grows with the number of data points (T). The bounds depend on the dimensionality (d) and hyperparameters (ν, l) of the kernel. For example, the linear kernel’s complexity grows logarithmically with T and linearly with the dimension d, while the RBF kernel’s complexity grows polynomially with T and logarithmically with the dimension d. The Matérn kernel’s complexity is a more complex function of T, d, ν and l.

In-depth insights

#

Nonepisodic RL

#

Nonepisodic reinforcement learning (RL) addresses a crucial limitation of traditional episodic RL, removing the requirement for resets between learning episodes. This is particularly relevant for real-world applications where resets are impractical or impossible, such as robotics or autonomous systems. The challenge lies in ensuring stability and preventing the system from diverging during continuous learning. Existing solutions often focus on linear systems with quadratic costs, limiting applicability. The paper introduces a novel approach, which uses optimism in the face of uncertainty to guide exploration and control in nonlinear systems. This optimism is integrated into a model-based algorithm, providing theoretical guarantees such as regret bounds. Empirical results show significant performance improvements over existing baselines, indicating the promise of this method for real-world control problems.

Optimistic Exploration

#

Optimistic exploration in reinforcement learning (RL) is a strategy that addresses the exploration-exploitation dilemma by actively searching for the most promising areas of the state-action space. It’s based on the principle of optimism in the face of uncertainty: the agent assumes the best possible outcome when dealing with incomplete knowledge of the environment. This approach contrasts with purely random exploration methods by focusing its exploration efforts where the potential reward is highest based on existing knowledge and uncertainty estimations. Well-calibrated probabilistic models are crucial for effective optimistic exploration. They provide not only estimates of expected rewards but also quantifiable uncertainties associated with those estimates. This allows the agent to balance exploration in areas of high uncertainty with exploitation of currently known high-reward areas. The effectiveness of optimistic exploration often relies on using computationally efficient planning algorithms that can work with uncertainty, leading to computationally tractable solutions even in complex environments. A key advantage is its ability to reduce the regret (difference between actual performance and optimal performance) in learning by intelligently guiding exploration. However, successful implementation needs careful consideration of uncertainty quantification and planning algorithms, and its performance depends heavily on the accuracy of the models used to estimate rewards and uncertainty.

Regret Bound Analysis

#

A regret bound analysis for a reinforcement learning algorithm assesses its performance by quantifying the difference between its cumulative cost and that of an optimal policy. For nonepisodic settings, where the agent learns continuously without resets, deriving tight regret bounds is particularly challenging. The analysis often involves intricate mathematical arguments, leveraging tools from probability, optimization, and dynamical systems. Key assumptions include the nature of the system dynamics (e.g., linearity, continuity), the stochasticity of the environment (e.g., Gaussian noise), and properties of the policy class (e.g., bounded energy). The analysis aims to show that the algorithm’s regret grows sublinearly with the number of time steps, indicating that the algorithm learns efficiently and approaches optimality over time. Crucially, the derived regret bounds depend on parameters related to the problem’s complexity, such as the information gain or the smoothness of the dynamics. This informs practical considerations on algorithm design choices and applicability to various real-world scenarios. Specific techniques for model calibration and uncertainty quantification play a crucial role in the analysis, ensuring reliability of the optimistic policy selection strategy that the algorithm employs.

Model-Based RL

#

Model-based reinforcement learning (RL) methods stand out due to their sample efficiency compared to model-free counterparts. They function by constructing a model of the environment’s dynamics, allowing agents to plan actions and evaluate their potential consequences through simulations. This approach avoids the need for extensive trial-and-error learning, making it particularly suitable for scenarios with limited data or high cost of interaction. However, model accuracy is crucial, as inaccuracies can lead to poor performance or instability. The success of model-based RL hinges on effectively balancing the need for accurate model representations with the computational resources required for planning. Effective exploration strategies are also essential; the agent must explore the environment adequately to build an accurate model, but excessive exploration can be wasteful. Recent advances have incorporated techniques like uncertainty estimation and optimistic planning to guide exploration efficiently. The choice of model representation (e.g., linear, nonlinear, Gaussian processes, neural networks) significantly influences both performance and computational demands. Model-based RL’s strength lies in its potential to generalize well, transferring knowledge to new environments similar to those used for training.

Future Work

#

The “Future Work” section of this research paper would ideally delve into several promising avenues. Extending the theoretical analysis beyond Gaussian process dynamics to encompass more general model classes (like Bayesian neural networks) would be crucial for broader applicability. Investigating tighter regret bounds and exploring lower bound analysis would further strengthen the theoretical foundation. Practical improvements, such as adaptive horizon selection and more efficient optimization strategies for the MPC subproblem, could enhance NEORL’s performance. Finally, applying NEORL to real-world scenarios and conducting extensive experimental evaluation on high-dimensional systems with diverse reward structures would not only showcase its effectiveness, but also identify potential limitations and guide future algorithm refinements.

More visual insights

#

More on tables

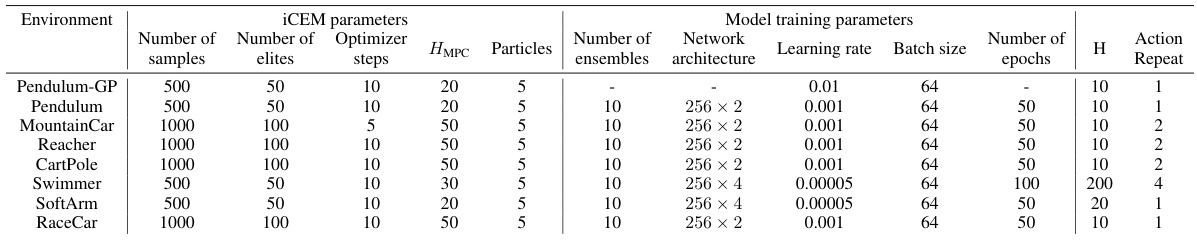
This table lists the hyperparameters used in the experiments presented in Section 4 of the paper. For each environment (Pendulum-GP, Pendulum, MountainCar, Reacher, CartPole, Swimmer, SoftArm, RaceCar), it provides details on the iCEM parameters (number of samples, number of elites, number of optimizer steps, HMPC horizon, number of particles) and the model training parameters (number of ensembles, network architecture, learning rate, batch size, number of epochs, action repeat). The hyperparameters were tuned for each environment to optimize performance.

This table lists the hyperparameters used for the experiments in Section 4 of the paper. It includes settings for the iCEM optimizer (number of particles, elites, steps, repeat), model training (number of samples, network architecture, learning rate, batch size, number of epochs), and the horizon H for each environment. The values are specific to each environment (Pendulum-GP, Pendulum, MountainCar, Reacher, CartPole, Swimmer, SoftArm, RaceCar).

Full paper

#